第二章不等式2.1 不等式的基本性质 课件(共33张PPT)
文档属性
| 名称 | 第二章不等式2.1 不等式的基本性质 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 18:01:32 | ||
图片预览











文档简介
(共33张PPT)
2.1 不等式的基本性质
心中有山河
与相等关系相比,不等关系在现实世界中更为普遍.我们知道,不等式就是描述不等关系的一种重要的数学表示形式,我们将通过实数大小的比较,来研究不等式的基本性质.
心中有山河
实数的大小
2.1.1
心中有山河
情境导入
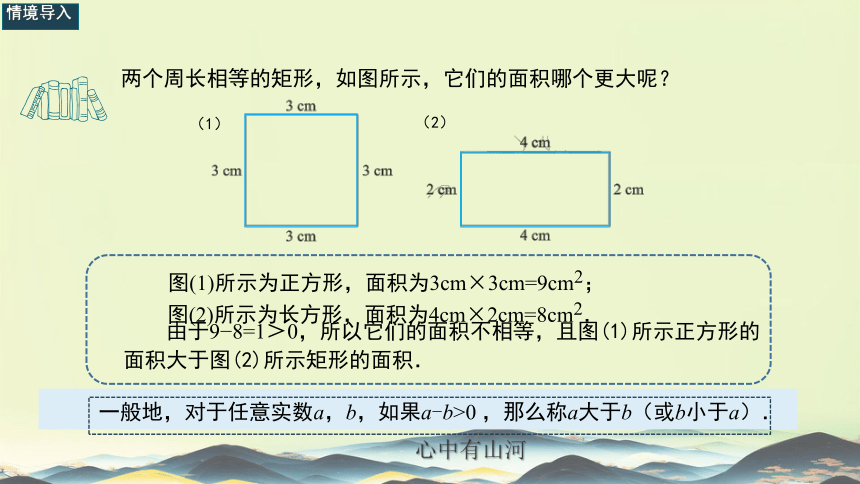
两个周长相等的矩形,如图所示,它们的面积哪个更大呢?
图(1)所示为正方形,面积为3cm×3cm=9cm2;
图(2)所示为长方形,面积为4cm×2cm=8cm2.
由于9 8=1>0,所以它们的面积不相等,且图(1)所示正方形的面积大于图(2)所示矩形的面积.
一般地,对于任意实数a,b,如果a-b>0 ,那么称a大于b(或b小于a).
(1)
(2)
心中有山河
探索新知
因为实数与数轴上的点是一一对应的,对于任意实数a、b都可以在数轴上找到对应的点A和B,如图所示.
显然,当点A在点B的右边时, a>b ;
当点A在点B的左边时, a当点A与点B重合时, a=b .
探索新知
心中有山河
关于实数a,b的大小关系,可以通过以下运算来表示:
a > b a-b > 0,
a < b a-b < 0,
a = b a-b = 0 .
要比较两个实数(或代数式)的大小,可以转化为比较它们的差与0的大小.这种比较大小的方法称为作差比较法.
读一读
“ ”表示“等价于”,即可以互相推出 .
探索新知
探索新知
心中有山河
典型例题
例1 比较 与 的大小.
解 因为
所以 .
心中有山河
例2 比较(x+1)(x+2)与3x-1的大小.
典型例题
解 因为(x+1)(x+2)-(3x-1)=(x +3x+2)-(3x-1) =x +3>0,
所以 (x+1)(x+2)>3x-1.
心中有山河
例3 比较 2x -x 与x +2x-3的大小.
典型例题
心中有山河
设a,b均为实数,试比较a +b -ab与ab的大小.
心中有山河
不等式入门性质
巩固练习
1.比较下列各组实数的大小.
(1) 与 ; (2) 与 ; (2) 与0.83.
2.若a>b ,比较2a-1 与2b-1 的大小.
3.比较x -1与2x +3 的大小.
练习
4.比较 x -x 与x-2 的大小.
心中有山河
不等式的性质
2.1.2
心中有山河
情境导入
比较两个实数大小的作差比较法为研究不等关系奠定了基础.那么,如何用这个方法研究不等式的性质呢?
心中有山河
不等式进阶性质
在义务教育阶段,我们学习过一些不等式的性质,如:
性质1 如果a>b,那么a+c>b+c.
探索新知
心中有山河
可以用作差比较法证明性质1.
由 a > b,得 a-b>0,于是
(a+c)-(b+c)= a+c-b-c =a-b >0 .
所以
a + c >b + c .
性质1的证明
探索新知
心中有山河
性质1的证明
也可以借助数轴来看性质1,如图所示.
性质1的证明
探索新知
心中有山河
性质1表明,不等式两边同时加上(或减去)同一个数(或代数式),不等号的方向不变.因此性质1也称为不等式的加法法则.
利用不等式的加法法则,容易证明:
如果 ,那么 .
这表明,不等式的任何一项可以从不等式的一边移到另一边,但同时要改变符号.这条结论也称为移项法则.
探索新知
心中有山河
性质2 如果a>b,c>0 ,那么ac>bc;
如果a>b,c<0,那么ac< bc.
探索新知
性质2表明,不等式两边同时乘(或除以)同一个正数,不等号的方向不变;不等式两边同时乘(或除以)同一个负数,不等号的方向改变.
性质2也称为不等式的乘法法则.
试一试
用作差比较法证明性质2.
心中有山河
探索新知
证明 由a>b, b>c ,得
a-b>0,b-c>0;
所以
a-c=a-b+b c=(a-b)+(b-c)>0,
由此得 a>c.
性质3 如果a>b,b>c,那么a>c.
性质3表明不等式具有传递性.
心中有山河
探索新知
我们也可以借助数轴来看不等式的传递性.
心中有山河
探索新知
性质4也称为同向不等式的可加性.
性质4 如果a>b,c>d,那么a+c>b+d.
证明 由a>b, c>d ,由性质1,得
a+c>b+c, b+c > b+d.
由性质3,得
a+c>b+d.
心中有山河
例4 用符号“>”或“<”填空,并说明利用了不等式的哪(几)条基本性质.
典型例题
心中有山河
例4 用符号“>”或“<”填空,并说明利用了不等式的哪(几)条基本性质.
典型例题
解
读一读
本题也可以根据不等式的性质1和性质3,由a+4>b+4>b+2得到 .
心中有山河
解
例4 用符号“>”或“<”填空,并说明利用了不等式的哪(几)条基本性质.
典型例题
, ;
心中有山河
解
例4 用符号“>”或“<”填空,并说明利用了不等式的哪(几)条基本性质.
典型例题
(4)如果a>b,那么3a-2 3b-3 .
心中有山河
典型例题
例5 若 , ,试证明 .
解 因为a>b,c>0 ,由不等式的性质2得
ac>bc.
同理,由c>d,b>0 ,得
bc>bd.
因此,由不等式的性质3可得ac>bd .
读一读
本题也是不等式的性质之一:两边都是正数的同向不等式,两边分别相乘,所得到的不等式与原不等式同向.
心中有山河
典型例题
例6 如果代数式 与代数式 的差不大于2,
求x的取值范围.
解 由题可知 ,
化简得 ,
因此 ,
故 .
所以x的取值范围是 .
心中有山河
如果a>b,c>d,是否有“a-c> b-d ”成立呢?如果成立,请说明理由;否则,请举出反例.
心中有山河
练习
巩固练习
1.已知a>b,用符号“>”或“<”填空:
(1)a+1 b+1;
(2)-5a -5b;
(3)3a+3 3b+2.
心中有山河
练习
巩固练习
3.如果代数式 与代数式 的差不小于3,求x的取值范围.
心中有山河
归纳总结
心中有山河
布置作业
心中有山河
感谢聆听
再见
心中有山河
2.1 不等式的基本性质
心中有山河
与相等关系相比,不等关系在现实世界中更为普遍.我们知道,不等式就是描述不等关系的一种重要的数学表示形式,我们将通过实数大小的比较,来研究不等式的基本性质.
心中有山河
实数的大小
2.1.1
心中有山河
情境导入
两个周长相等的矩形,如图所示,它们的面积哪个更大呢?
图(1)所示为正方形,面积为3cm×3cm=9cm2;
图(2)所示为长方形,面积为4cm×2cm=8cm2.
由于9 8=1>0,所以它们的面积不相等,且图(1)所示正方形的面积大于图(2)所示矩形的面积.
一般地,对于任意实数a,b,如果a-b>0 ,那么称a大于b(或b小于a).
(1)
(2)
心中有山河
探索新知
因为实数与数轴上的点是一一对应的,对于任意实数a、b都可以在数轴上找到对应的点A和B,如图所示.
显然,当点A在点B的右边时, a>b ;
当点A在点B的左边时, a当点A与点B重合时, a=b .
探索新知
心中有山河
关于实数a,b的大小关系,可以通过以下运算来表示:
a > b a-b > 0,
a < b a-b < 0,
a = b a-b = 0 .
要比较两个实数(或代数式)的大小,可以转化为比较它们的差与0的大小.这种比较大小的方法称为作差比较法.
读一读
“ ”表示“等价于”,即可以互相推出 .
探索新知
探索新知
心中有山河
典型例题
例1 比较 与 的大小.
解 因为
所以 .
心中有山河
例2 比较(x+1)(x+2)与3x-1的大小.
典型例题
解 因为(x+1)(x+2)-(3x-1)=(x +3x+2)-(3x-1) =x +3>0,
所以 (x+1)(x+2)>3x-1.
心中有山河
例3 比较 2x -x 与x +2x-3的大小.
典型例题
心中有山河
设a,b均为实数,试比较a +b -ab与ab的大小.
心中有山河
不等式入门性质
巩固练习
1.比较下列各组实数的大小.
(1) 与 ; (2) 与 ; (2) 与0.83.
2.若a>b ,比较2a-1 与2b-1 的大小.
3.比较x -1与2x +3 的大小.
练习
4.比较 x -x 与x-2 的大小.
心中有山河
不等式的性质
2.1.2
心中有山河
情境导入
比较两个实数大小的作差比较法为研究不等关系奠定了基础.那么,如何用这个方法研究不等式的性质呢?
心中有山河
不等式进阶性质
在义务教育阶段,我们学习过一些不等式的性质,如:
性质1 如果a>b,那么a+c>b+c.
探索新知
心中有山河
可以用作差比较法证明性质1.
由 a > b,得 a-b>0,于是
(a+c)-(b+c)= a+c-b-c =a-b >0 .
所以
a + c >b + c .
性质1的证明
探索新知
心中有山河
性质1的证明
也可以借助数轴来看性质1,如图所示.
性质1的证明
探索新知
心中有山河
性质1表明,不等式两边同时加上(或减去)同一个数(或代数式),不等号的方向不变.因此性质1也称为不等式的加法法则.
利用不等式的加法法则,容易证明:
如果 ,那么 .
这表明,不等式的任何一项可以从不等式的一边移到另一边,但同时要改变符号.这条结论也称为移项法则.
探索新知
心中有山河
性质2 如果a>b,c>0 ,那么ac>bc;
如果a>b,c<0,那么ac< bc.
探索新知
性质2表明,不等式两边同时乘(或除以)同一个正数,不等号的方向不变;不等式两边同时乘(或除以)同一个负数,不等号的方向改变.
性质2也称为不等式的乘法法则.
试一试
用作差比较法证明性质2.
心中有山河
探索新知
证明 由a>b, b>c ,得
a-b>0,b-c>0;
所以
a-c=a-b+b c=(a-b)+(b-c)>0,
由此得 a>c.
性质3 如果a>b,b>c,那么a>c.
性质3表明不等式具有传递性.
心中有山河
探索新知
我们也可以借助数轴来看不等式的传递性.
心中有山河
探索新知
性质4也称为同向不等式的可加性.
性质4 如果a>b,c>d,那么a+c>b+d.
证明 由a>b, c>d ,由性质1,得
a+c>b+c, b+c > b+d.
由性质3,得
a+c>b+d.
心中有山河
例4 用符号“>”或“<”填空,并说明利用了不等式的哪(几)条基本性质.
典型例题
心中有山河
例4 用符号“>”或“<”填空,并说明利用了不等式的哪(几)条基本性质.
典型例题
解
读一读
本题也可以根据不等式的性质1和性质3,由a+4>b+4>b+2得到 .
心中有山河
解
例4 用符号“>”或“<”填空,并说明利用了不等式的哪(几)条基本性质.
典型例题
, ;
心中有山河
解
例4 用符号“>”或“<”填空,并说明利用了不等式的哪(几)条基本性质.
典型例题
(4)如果a>b,那么3a-2 3b-3 .
心中有山河
典型例题
例5 若 , ,试证明 .
解 因为a>b,c>0 ,由不等式的性质2得
ac>bc.
同理,由c>d,b>0 ,得
bc>bd.
因此,由不等式的性质3可得ac>bd .
读一读
本题也是不等式的性质之一:两边都是正数的同向不等式,两边分别相乘,所得到的不等式与原不等式同向.
心中有山河
典型例题
例6 如果代数式 与代数式 的差不大于2,
求x的取值范围.
解 由题可知 ,
化简得 ,
因此 ,
故 .
所以x的取值范围是 .
心中有山河
如果a>b,c>d,是否有“a-c> b-d ”成立呢?如果成立,请说明理由;否则,请举出反例.
心中有山河
练习
巩固练习
1.已知a>b,用符号“>”或“<”填空:
(1)a+1 b+1;
(2)-5a -5b;
(3)3a+3 3b+2.
心中有山河
练习
巩固练习
3.如果代数式 与代数式 的差不小于3,求x的取值范围.
心中有山河
归纳总结
心中有山河
布置作业
心中有山河
感谢聆听
再见
心中有山河
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
