【章节考点培优】2.1代数式的概念和列代数式-2025-2026学年七年级上册数学湘教版(2024)(含答案解析)
文档属性
| 名称 | 【章节考点培优】2.1代数式的概念和列代数式-2025-2026学年七年级上册数学湘教版(2024)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 258.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 21:22:58 | ||
图片预览




文档简介
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年七年级上册数学单元考点培优湘教版(2024)
第2章 代数式 2.1 代数式的概念和列代数式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各式符合代数式书写规范的是( )
A.x5 B. C.m+n元 D.
2.下列说法正确的是( )
A.0、b、都是单项式
B.单项式a没有次数
C.是代数式
D.是由、、三项组成
3.长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )
A.2a2-πb2 B.2a2-b2 C.2ab-πb2 D.2ab-b2
4.一次知识竞赛共有20道选择题,规定:答对一道得5分,不答或答错一道扣1分,如果某位学生答对了x道题,则用式子表示他的成绩为( )
A.5x﹣(20+x) B.100﹣(20﹣x)
C.5x D.5x﹣(20﹣x)
5. 若x表示某件物品的原价,则式子(1-10%)x表示的意义是( )
A.该物品价格上涨10%时上涨的价格
B.该物品价格下降10%时下降的价格
C.该物品价格上涨10%后的售价
D.该物品价格下降10%后的售价
6.某公司今年2月份的利润为x 万元,3月份比2月份减少7%,4月份比3月份增加了8%,则该公司4月份的利润为 ( )
A.(x-7%)(x+8%)万元 B.(x-7%+8%)万元
C.(1-7%+8%)x万元 D.(1-7%)(1+8%)x万元
7.某种商品原价每件m元,第一次降价打“八折”,第二次降价每件减10元,则第二次降价后的售价是( )
A.元 B.元 C.元 D.元
8.随着计算机技术的迅速发展,电脑价格不断降低.某品牌电脑原价n元,先降价20%后再降低m元,那么该电脑的现价为( )
A. 元 B. 元 C. 元 D. 元
9.风力发电是一种常见的绿色环保发电形式,它能够使大自然的资源得到更好地利用.如图1,风力发电机有三个底端重合、两两成角的叶片,以三个叶片的重合点为原点,水平方向为轴建立平面直角坐标系(如图2所示),已知开始时其中一个叶片的外端点的坐标为,在一段时间内,叶片每秒绕原点顺时针转动,则第时,点的对应点的坐标为( )
A. B. C. D.
10.如图,要围一个矩形菜园ABCD,其中一边AD是墙,其余的三边 AB、BC、CD用篱笆围成,且这三边的和为40 米.若设BC的长a 米,则AB的长度可以表示为( )
A. 米 B.(40-2a)米 C.米 D.(20-a)米
二、填空题
11.两个连续的偶数,前面的数是a,则后面的数是 .
12.某校校区门口是交通主干道,为缓解交通压力及解决交通安全隐患,实行整队分流错峰放学.七年级新生在开学第一周放学时每分钟约a人分流离校,后经指导,七年级新生提高认识,整队迅速,各班无缝衔接,放学时每分钟多分流b人,现在8分钟时间七年级新生放学分流离校人数约 人.
13.如图,用灰白两色正方形瓷砖铺设地面,第5个图案中灰色瓷砖块数为 块,第个图案中白色瓷砖块数为 块.(用含的代数式表示)
14.由2x﹣3y﹣4=0,可以得到用x表示y的式子y=
15.甲、乙两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是,水流速度是,后甲船比乙船多航行 千米
16.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…若点A(,0),B(0,2),则点A2023的坐标是 .
三、计算题
17.如图,两个正方形的边长分别是和.
(1)用含的式子表示图中阴影部分的面积,并化简;
(2)当时,计算阴影部分的面积.
四、解答题
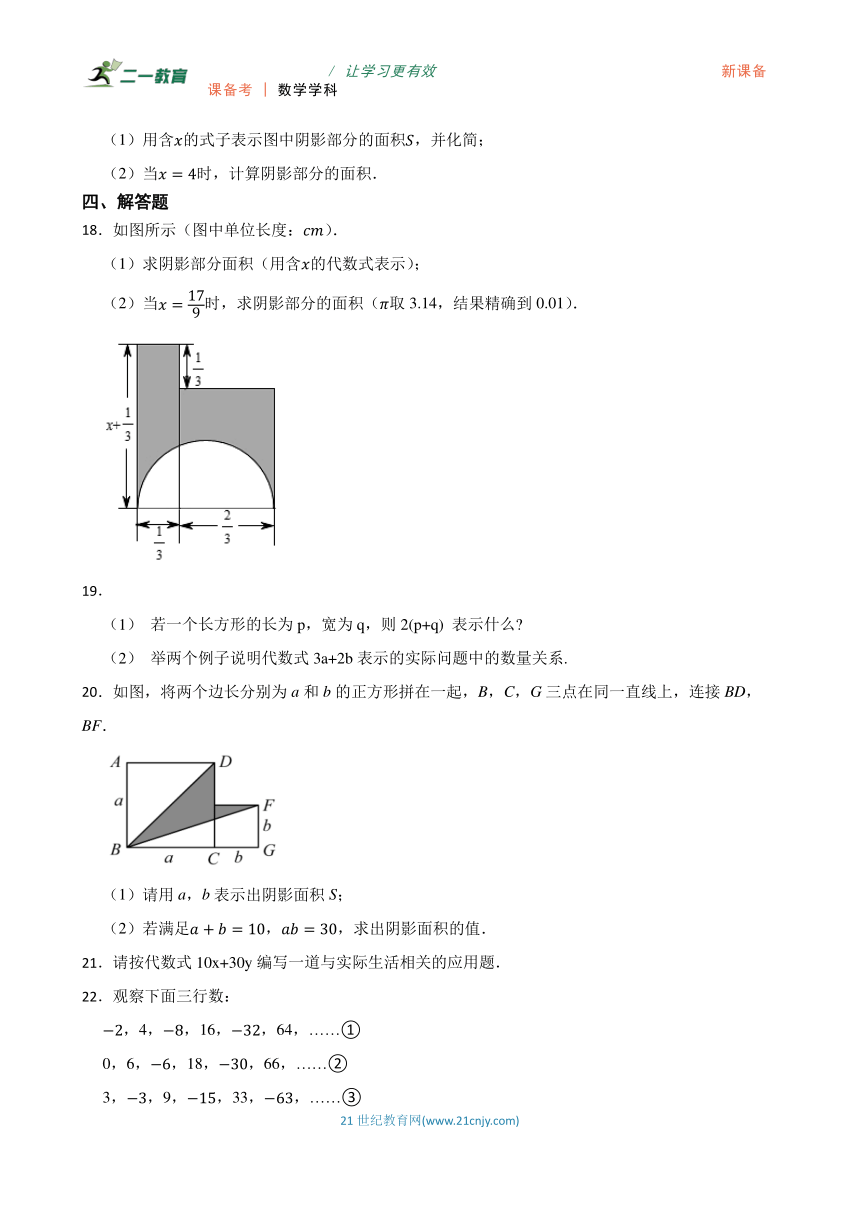
18.如图所示(图中单位长度:).
(1)求阴影部分面积(用含的代数式表示);
(2)当时,求阴影部分的面积(取3.14,结果精确到0.01).
19.
(1) 若一个长方形的长为p,宽为q,则2(p+q) 表示什么
(2) 举两个例子说明代数式3a+2b表示的实际问题中的数量关系.
20.如图,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD,BF.
(1)请用a,b表示出阴影面积S;
(2)若满足,,求出阴影面积的值.
21.请按代数式10x+30y编写一道与实际生活相关的应用题.
22.观察下面三行数:
,4,,16,,64,……①
0,6,,18,,66,……②
3,,9,,33,,……③
(1)第①行数的第个数是___________;
(2)请将第②行数中的每一个数分别减去第①行数中对应位置的数,并找出规律,根据你得到的结论,直接写出第②行数的第个数是___________;同理直接写出第③行数的第个数是___________;
(3)如果取每行的第个数,这三个数的和能否等于?若能,请求出的值;若不能,请说明理由.
(4)第③行中是否存在连续的三个数的和为99,若存在,直接写出这三个数;若不存在,则说明理由.
23.什么样的两个数的和等于它们的积呢?你大概马上会想到2+2=2×2,其实这样的两个数还有很多,例如,3+ =3×
(1)请再写出两个这样的等式.
(2)你能从中发现什么规律?把它用字母n表示出来.
参考答案及试题解析
1.B
【解答】解:A、x5应该书写为5x,所以A选项不符合题意;
B、 书写规范,所以B选项符合题意;
C、m+n元应该书写为(m+n)元,所以C选项不符合题意;
D、 应该书写为 ,所以D选项不符合题意.
故答案为:B.
【分析】根据代数式的书写要求逐项判定即可。
2.C
【解答】A、0、b是单项式,是多项式,故选项A错误;
B、单项式a的次数是1,故选项B错误;
C、是代数式,故选项C正确;
D、是由、、三项组成,故选项D错误.
故选:C.
【分析】根据单项式的定义可判断A选项,根据多项式的次数可判断B选项,根据代数式的定义可判断C选项,根据多项式的项可判断D选项.
3.D
【解答】解:根据题意得:射进阳光部分的面积为:;
故答案为:D.
【分析】利用圆的面积、长方形的面积公式及“ 射进阳光部分的面积=长方形的面积-阴影部分的面积 ”列出代数式即可.
4.D
【解答】解:由题意可得,
他的成绩是:5x-(20-x),
故答案为:D.
【分析】用答对的分数减去不答或答错的分数即可得到答案。
5.D
【解答】解:若x表示某件物品的原价,则代数式(1 - 10%) x表示的意义是该物品价格下降10%后的售价;
故答案为:D.
【分析】用字母表示数注意事项:数和表示数得字母相乘,字母和字母相乘时,乘号可以省略不写,或用“·”号代替。数和字母相乘,在省略乘号时,要把数字写在字母得前面。如n×2写称2n,一般不能写成n2.
6.D
【解答】解:∵该公司今年2月份的利润为x 万元,3月份比2月份减少7%,4月份比3月份增加了8%,
∴四月份的利润为(1-7%)(1+8%)x万元.
故答案为:D
【分析】3月份比2月份减少7%,则3月份的利润是2月份的(1-7%);4月份比3月份增加8%,则4月份的利润是3月份的(1+8%);据此即可列出代数式.
7.D
【解答】解:根据题意,得:第二次降价后的售价为:元;
故答案为:D.
【分析】利用“折扣价=原价×折扣率 ”求出第一次价格,再根据“ 第二次降价每件减10元 ”列出代数式即可.
8.C
【解答】解:由题意可得:该电脑的现价为:n(1-20%)-m= .
故答案为:C.
【分析】该电脑的现价=原价×(1-20%)再减去m,化简即可.
9.B
【解答】解:∵,
∴A在第一象限的角平分线上,
∵叶片每秒绕原点顺时针转动,
∴,,,,
∴点A的坐标以每4秒为一个周期依次循环,
∵,
∴第时,点A的对应点的坐标与相同,为.
故选:B.
【分析】
根据旋转的性质分别求出第1、2、3、4s时,点A的对应点、、、的坐标,找到规律,进而得出第时,点A的对应点的坐标.
10.C
【解答】由题意:AB可表示为: 米 ,
故答案为:C.
【分析】根据图形以及三边 AB、BC、CD的和为40 米,再由BC为a即可求解.
11.
【解答】解:由题意知, 前面的数是a时,后面的数是,
故答案为:.
【分析】相邻的两个偶数相差2,据此求解作答即可.
12.
【解答】解:由题意得,整队后每分钟七年级新生放学分流离校人数为人,
∴现在8分钟时间七年级新生放学分流离校人数约人,
故答案为:.
【分析】由题意可得整队后每分钟七年级新生放学分流离校人数,再乘以8即可求出答案.
13.12;
【解答】解:由图可得:
第1个图案中灰色瓷砖块数为:(块);白色瓷砖块数为:(块);
第2个图案中灰色瓷砖块数为:(块);白色瓷砖块数为:(块);
第3个图案中灰色瓷砖块数为:(块);白色瓷砖块数为:(块);
....
第5个图案中灰色瓷砖块数为:(块);白色瓷砖块数为:(块);
依此类推,第个图案中灰色瓷砖块数为:(块); 瓷砖块数为:(块);
故答案为:;.
【分析】根据图形观察其规律,灰色瓷砖每次多两块,白色瓷砖每次多三块,列出式子即可.
14.y=x﹣
【解答】解:移项得:﹣3y=4﹣2x,
系数化1得:y=﹣(4﹣2x)=x﹣.
【分析】要把方程2x﹣3y﹣4=0写成用含x的式子表示y的形式, 需要把含有y的项移到等号一边,其他的项移到另一边,然后合并同类项、系数化1
15.
【解答】解:甲船顺水,乙船逆水,两船在静水中的速度都是,水流速度是,
甲船的速度为,乙船的速度为,
后甲船比乙船多航行距离为
(千米),
故答案为:.
【分析】本题考查列代数式解决应用题.根据船在顺水中的速度=船的速度+水的速度,可将甲船顺水速度用代数式表示出来,根据船在逆水中的速度=船的速度—水的速度,可将乙船逆水速度用代数式表示出来,再根据距离速度时间可列出式子:,再进行化简可求出答案.
16.
【解答】解:由题意得,
由勾股定理得:,
∴,
∴,…,
∵,,
∴,
故答案为:.
【分析】根据已知条件三角形的三边长度,然后通过旋转发现,…,按照规律可得出点的坐标.
17.(1)解:由题意知,阴影部分的面积=两个正方形的面积减去上面两个小直角三角形的面积再减去下面大直角三角形的面积,
即
;
(2)解:当时,,
∴阴影部分的面积为.
【分析】(1)根据阴影部分的面积=两个正方形的面积减去上面两个小直角三角形的面积再减去下面大直角三角形的面积列出式子,并化简即可;
(2)把x的值代入(1)的结果中即可得出阴影部分的面积.
18.解:(1)阴影部分的面积:
(2)当时,阴影部分的面积
故答案为:(1);(2).
【分析】(1)利用“阴影面积=两个长方形的面积和半圆的面积”列出代数式,再求解即可;
(2)将代入计算即可.
19.(1)解: 长方形的长为p,宽为q,则2(p+q) 表示表示长方形的周长;
(2)解:每千克苹果的价格为a元,每千克橘子的价格为b元,那么3千克苹果和2千克橘子的价钱是( 3a+2b )元;
大笔记本每本a元,小笔记本每本b元,买3本大笔记本和2本小笔记本共需( 3a+2b )元;
【分析】(1)根据长方形的周长公式即可求解;
(2) 举出实例说明代数式3a+2b表示的实际问题中的数量关系即可.
20.(1)解:连接CF,DF,如图:
∴
(2)解:当,,
∴
【分析】(1)连接BE,于是阴影部分的面积可以表示成△DEB和△EFB的面积和.
(2)把,, 代入阴影面积求值即可.
21.解:答案不唯一.
如一个苹果的质量是x,一个桔子的质量是y,那么10个苹果和30个桔子的质量和是10x+30y.
【分析】结合实际情境作答,答案不唯一.
22.(1)解:∵,4,,16,,64.…;
∴这行数的第n个数为:,
故答案为:;
(2)解:∵,4,,16,,64.…;①
0,6,,18,,66,……②
3,,9,,33,,…;③
∴第②行中的每个数都是对应的第①行的数字加2得到的,第③的数字都是对应的第①行数字的相反数加1得到的,
∴第②行数的第n个数是:,第③行数的第n个数是,
故答案为:,;
(3)解:能,,理由如下,
设这三个数为:,,,
由题意可得,,
整理得,
解得,
即k的值是7;
故答案为:能,.
(4)解:能,,理由如下,
设这三个数为:,,,
由题意可得,,
整理得,即,
解得,
即这三个数为:33,,129.
故答案为:33,,129.
【分析】(1)根据题干中的数据与序号的关系可得规律这行数的第n个数为:;
(2)根据题干中的数据与序号的关系可得规律,再求出第②行数的第n个数是:,第③行数的第n个数是即可;
(3)设这三个数为:,,,再结合“ 这三个数的和等于 ”列出方程,再求解即可;
(4)设这三个数为:,,,再结合“ 三个数的和为99 ”列出方程,再求解即可.
(1)解:∵,4,,16,,64.…;
∴这行数的第n个数为:,
故答案为:;
(2)解:∵,4,,16,,64.…;①
0,6,,18,,66,……②
3,,9,,33,,…;③
∴第②行中的每个数都是对应的第①行的数字加2得到的,第③的数字都是对应的第①行数字的相反数加1得到的,
∴第②行数的第n个数是:,第③行数的第n个数是,
故答案为:,;
(3)解:能,,理由如下,
设这三个数为:,,,
由题意可得,,
整理得,
解得,
即k的值是7;
(4)解:能,,理由如下,
设这三个数为:,,,
由题意可得,,
整理得,即,
解得,
即这三个数为:33,,129.
23.(1)解:4+=4×.5+=5× (答案不唯一).
(2)解: (n>1,且n为整数).
【分析】(1)根据题意写出即可,答案不唯一;
(2)观察写出的等式即可得出规律.
21世纪教育网(www.21cnjy.com)
2025-2026学年七年级上册数学单元考点培优湘教版(2024)
第2章 代数式 2.1 代数式的概念和列代数式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各式符合代数式书写规范的是( )
A.x5 B. C.m+n元 D.
2.下列说法正确的是( )
A.0、b、都是单项式
B.单项式a没有次数
C.是代数式
D.是由、、三项组成
3.长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )
A.2a2-πb2 B.2a2-b2 C.2ab-πb2 D.2ab-b2
4.一次知识竞赛共有20道选择题,规定:答对一道得5分,不答或答错一道扣1分,如果某位学生答对了x道题,则用式子表示他的成绩为( )
A.5x﹣(20+x) B.100﹣(20﹣x)
C.5x D.5x﹣(20﹣x)
5. 若x表示某件物品的原价,则式子(1-10%)x表示的意义是( )
A.该物品价格上涨10%时上涨的价格
B.该物品价格下降10%时下降的价格
C.该物品价格上涨10%后的售价
D.该物品价格下降10%后的售价
6.某公司今年2月份的利润为x 万元,3月份比2月份减少7%,4月份比3月份增加了8%,则该公司4月份的利润为 ( )
A.(x-7%)(x+8%)万元 B.(x-7%+8%)万元
C.(1-7%+8%)x万元 D.(1-7%)(1+8%)x万元
7.某种商品原价每件m元,第一次降价打“八折”,第二次降价每件减10元,则第二次降价后的售价是( )
A.元 B.元 C.元 D.元
8.随着计算机技术的迅速发展,电脑价格不断降低.某品牌电脑原价n元,先降价20%后再降低m元,那么该电脑的现价为( )
A. 元 B. 元 C. 元 D. 元
9.风力发电是一种常见的绿色环保发电形式,它能够使大自然的资源得到更好地利用.如图1,风力发电机有三个底端重合、两两成角的叶片,以三个叶片的重合点为原点,水平方向为轴建立平面直角坐标系(如图2所示),已知开始时其中一个叶片的外端点的坐标为,在一段时间内,叶片每秒绕原点顺时针转动,则第时,点的对应点的坐标为( )
A. B. C. D.
10.如图,要围一个矩形菜园ABCD,其中一边AD是墙,其余的三边 AB、BC、CD用篱笆围成,且这三边的和为40 米.若设BC的长a 米,则AB的长度可以表示为( )
A. 米 B.(40-2a)米 C.米 D.(20-a)米
二、填空题
11.两个连续的偶数,前面的数是a,则后面的数是 .
12.某校校区门口是交通主干道,为缓解交通压力及解决交通安全隐患,实行整队分流错峰放学.七年级新生在开学第一周放学时每分钟约a人分流离校,后经指导,七年级新生提高认识,整队迅速,各班无缝衔接,放学时每分钟多分流b人,现在8分钟时间七年级新生放学分流离校人数约 人.
13.如图,用灰白两色正方形瓷砖铺设地面,第5个图案中灰色瓷砖块数为 块,第个图案中白色瓷砖块数为 块.(用含的代数式表示)
14.由2x﹣3y﹣4=0,可以得到用x表示y的式子y=
15.甲、乙两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是,水流速度是,后甲船比乙船多航行 千米
16.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…若点A(,0),B(0,2),则点A2023的坐标是 .
三、计算题
17.如图,两个正方形的边长分别是和.
(1)用含的式子表示图中阴影部分的面积,并化简;
(2)当时,计算阴影部分的面积.
四、解答题
18.如图所示(图中单位长度:).
(1)求阴影部分面积(用含的代数式表示);
(2)当时,求阴影部分的面积(取3.14,结果精确到0.01).
19.
(1) 若一个长方形的长为p,宽为q,则2(p+q) 表示什么
(2) 举两个例子说明代数式3a+2b表示的实际问题中的数量关系.
20.如图,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD,BF.
(1)请用a,b表示出阴影面积S;
(2)若满足,,求出阴影面积的值.
21.请按代数式10x+30y编写一道与实际生活相关的应用题.
22.观察下面三行数:
,4,,16,,64,……①
0,6,,18,,66,……②
3,,9,,33,,……③
(1)第①行数的第个数是___________;
(2)请将第②行数中的每一个数分别减去第①行数中对应位置的数,并找出规律,根据你得到的结论,直接写出第②行数的第个数是___________;同理直接写出第③行数的第个数是___________;
(3)如果取每行的第个数,这三个数的和能否等于?若能,请求出的值;若不能,请说明理由.
(4)第③行中是否存在连续的三个数的和为99,若存在,直接写出这三个数;若不存在,则说明理由.
23.什么样的两个数的和等于它们的积呢?你大概马上会想到2+2=2×2,其实这样的两个数还有很多,例如,3+ =3×
(1)请再写出两个这样的等式.
(2)你能从中发现什么规律?把它用字母n表示出来.
参考答案及试题解析
1.B
【解答】解:A、x5应该书写为5x,所以A选项不符合题意;
B、 书写规范,所以B选项符合题意;
C、m+n元应该书写为(m+n)元,所以C选项不符合题意;
D、 应该书写为 ,所以D选项不符合题意.
故答案为:B.
【分析】根据代数式的书写要求逐项判定即可。
2.C
【解答】A、0、b是单项式,是多项式,故选项A错误;
B、单项式a的次数是1,故选项B错误;
C、是代数式,故选项C正确;
D、是由、、三项组成,故选项D错误.
故选:C.
【分析】根据单项式的定义可判断A选项,根据多项式的次数可判断B选项,根据代数式的定义可判断C选项,根据多项式的项可判断D选项.
3.D
【解答】解:根据题意得:射进阳光部分的面积为:;
故答案为:D.
【分析】利用圆的面积、长方形的面积公式及“ 射进阳光部分的面积=长方形的面积-阴影部分的面积 ”列出代数式即可.
4.D
【解答】解:由题意可得,
他的成绩是:5x-(20-x),
故答案为:D.
【分析】用答对的分数减去不答或答错的分数即可得到答案。
5.D
【解答】解:若x表示某件物品的原价,则代数式(1 - 10%) x表示的意义是该物品价格下降10%后的售价;
故答案为:D.
【分析】用字母表示数注意事项:数和表示数得字母相乘,字母和字母相乘时,乘号可以省略不写,或用“·”号代替。数和字母相乘,在省略乘号时,要把数字写在字母得前面。如n×2写称2n,一般不能写成n2.
6.D
【解答】解:∵该公司今年2月份的利润为x 万元,3月份比2月份减少7%,4月份比3月份增加了8%,
∴四月份的利润为(1-7%)(1+8%)x万元.
故答案为:D
【分析】3月份比2月份减少7%,则3月份的利润是2月份的(1-7%);4月份比3月份增加8%,则4月份的利润是3月份的(1+8%);据此即可列出代数式.
7.D
【解答】解:根据题意,得:第二次降价后的售价为:元;
故答案为:D.
【分析】利用“折扣价=原价×折扣率 ”求出第一次价格,再根据“ 第二次降价每件减10元 ”列出代数式即可.
8.C
【解答】解:由题意可得:该电脑的现价为:n(1-20%)-m= .
故答案为:C.
【分析】该电脑的现价=原价×(1-20%)再减去m,化简即可.
9.B
【解答】解:∵,
∴A在第一象限的角平分线上,
∵叶片每秒绕原点顺时针转动,
∴,,,,
∴点A的坐标以每4秒为一个周期依次循环,
∵,
∴第时,点A的对应点的坐标与相同,为.
故选:B.
【分析】
根据旋转的性质分别求出第1、2、3、4s时,点A的对应点、、、的坐标,找到规律,进而得出第时,点A的对应点的坐标.
10.C
【解答】由题意:AB可表示为: 米 ,
故答案为:C.
【分析】根据图形以及三边 AB、BC、CD的和为40 米,再由BC为a即可求解.
11.
【解答】解:由题意知, 前面的数是a时,后面的数是,
故答案为:.
【分析】相邻的两个偶数相差2,据此求解作答即可.
12.
【解答】解:由题意得,整队后每分钟七年级新生放学分流离校人数为人,
∴现在8分钟时间七年级新生放学分流离校人数约人,
故答案为:.
【分析】由题意可得整队后每分钟七年级新生放学分流离校人数,再乘以8即可求出答案.
13.12;
【解答】解:由图可得:
第1个图案中灰色瓷砖块数为:(块);白色瓷砖块数为:(块);
第2个图案中灰色瓷砖块数为:(块);白色瓷砖块数为:(块);
第3个图案中灰色瓷砖块数为:(块);白色瓷砖块数为:(块);
....
第5个图案中灰色瓷砖块数为:(块);白色瓷砖块数为:(块);
依此类推,第个图案中灰色瓷砖块数为:(块); 瓷砖块数为:(块);
故答案为:;.
【分析】根据图形观察其规律,灰色瓷砖每次多两块,白色瓷砖每次多三块,列出式子即可.
14.y=x﹣
【解答】解:移项得:﹣3y=4﹣2x,
系数化1得:y=﹣(4﹣2x)=x﹣.
【分析】要把方程2x﹣3y﹣4=0写成用含x的式子表示y的形式, 需要把含有y的项移到等号一边,其他的项移到另一边,然后合并同类项、系数化1
15.
【解答】解:甲船顺水,乙船逆水,两船在静水中的速度都是,水流速度是,
甲船的速度为,乙船的速度为,
后甲船比乙船多航行距离为
(千米),
故答案为:.
【分析】本题考查列代数式解决应用题.根据船在顺水中的速度=船的速度+水的速度,可将甲船顺水速度用代数式表示出来,根据船在逆水中的速度=船的速度—水的速度,可将乙船逆水速度用代数式表示出来,再根据距离速度时间可列出式子:,再进行化简可求出答案.
16.
【解答】解:由题意得,
由勾股定理得:,
∴,
∴,…,
∵,,
∴,
故答案为:.
【分析】根据已知条件三角形的三边长度,然后通过旋转发现,…,按照规律可得出点的坐标.
17.(1)解:由题意知,阴影部分的面积=两个正方形的面积减去上面两个小直角三角形的面积再减去下面大直角三角形的面积,
即
;
(2)解:当时,,
∴阴影部分的面积为.
【分析】(1)根据阴影部分的面积=两个正方形的面积减去上面两个小直角三角形的面积再减去下面大直角三角形的面积列出式子,并化简即可;
(2)把x的值代入(1)的结果中即可得出阴影部分的面积.
18.解:(1)阴影部分的面积:
(2)当时,阴影部分的面积
故答案为:(1);(2).
【分析】(1)利用“阴影面积=两个长方形的面积和半圆的面积”列出代数式,再求解即可;
(2)将代入计算即可.
19.(1)解: 长方形的长为p,宽为q,则2(p+q) 表示表示长方形的周长;
(2)解:每千克苹果的价格为a元,每千克橘子的价格为b元,那么3千克苹果和2千克橘子的价钱是( 3a+2b )元;
大笔记本每本a元,小笔记本每本b元,买3本大笔记本和2本小笔记本共需( 3a+2b )元;
【分析】(1)根据长方形的周长公式即可求解;
(2) 举出实例说明代数式3a+2b表示的实际问题中的数量关系即可.
20.(1)解:连接CF,DF,如图:
∴
(2)解:当,,
∴
【分析】(1)连接BE,于是阴影部分的面积可以表示成△DEB和△EFB的面积和.
(2)把,, 代入阴影面积求值即可.
21.解:答案不唯一.
如一个苹果的质量是x,一个桔子的质量是y,那么10个苹果和30个桔子的质量和是10x+30y.
【分析】结合实际情境作答,答案不唯一.
22.(1)解:∵,4,,16,,64.…;
∴这行数的第n个数为:,
故答案为:;
(2)解:∵,4,,16,,64.…;①
0,6,,18,,66,……②
3,,9,,33,,…;③
∴第②行中的每个数都是对应的第①行的数字加2得到的,第③的数字都是对应的第①行数字的相反数加1得到的,
∴第②行数的第n个数是:,第③行数的第n个数是,
故答案为:,;
(3)解:能,,理由如下,
设这三个数为:,,,
由题意可得,,
整理得,
解得,
即k的值是7;
故答案为:能,.
(4)解:能,,理由如下,
设这三个数为:,,,
由题意可得,,
整理得,即,
解得,
即这三个数为:33,,129.
故答案为:33,,129.
【分析】(1)根据题干中的数据与序号的关系可得规律这行数的第n个数为:;
(2)根据题干中的数据与序号的关系可得规律,再求出第②行数的第n个数是:,第③行数的第n个数是即可;
(3)设这三个数为:,,,再结合“ 这三个数的和等于 ”列出方程,再求解即可;
(4)设这三个数为:,,,再结合“ 三个数的和为99 ”列出方程,再求解即可.
(1)解:∵,4,,16,,64.…;
∴这行数的第n个数为:,
故答案为:;
(2)解:∵,4,,16,,64.…;①
0,6,,18,,66,……②
3,,9,,33,,…;③
∴第②行中的每个数都是对应的第①行的数字加2得到的,第③的数字都是对应的第①行数字的相反数加1得到的,
∴第②行数的第n个数是:,第③行数的第n个数是,
故答案为:,;
(3)解:能,,理由如下,
设这三个数为:,,,
由题意可得,,
整理得,
解得,
即k的值是7;
(4)解:能,,理由如下,
设这三个数为:,,,
由题意可得,,
整理得,即,
解得,
即这三个数为:33,,129.
23.(1)解:4+=4×.5+=5× (答案不唯一).
(2)解: (n>1,且n为整数).
【分析】(1)根据题意写出即可,答案不唯一;
(2)观察写出的等式即可得出规律.
21世纪教育网(www.21cnjy.com)
同课章节目录
