【章节考点培优】3.3一元一次方程的解法-2025-2026学年七年级上册数学湘教版(2024)(含答案解析)
文档属性
| 名称 | 【章节考点培优】3.3一元一次方程的解法-2025-2026学年七年级上册数学湘教版(2024)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 111.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 21:31:39 | ||
图片预览




文档简介
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年七年级上册数学单元考点培优湘教版(2024)
第3章 一次方程(组) 3.3 一元一次方程的解法
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若、表示非零常数,整式的值随的取值而发生变化,如下表,则关于的一元一次方程的解为( )
0 1 3 ……
1 3 5 9 ……
A. B. C. D.
2.把方程去分母后,正确的结果是( )
A. B.
C. D.
3.在解方程时,去括号正确的是( )
A. B.
C. D.
4.下列解方程中变形正确的有( )
①变形为;②变形为;③变形为;④变形为;⑤变形为.
A.①②④ B.②③④ C.①③⑤ D.②④⑤
5.小马虎做作业时,不小心将方程中的一个常数污染了,被污染的方程是2(x-3)-■=x+1,怎么办呢?他想了想,便翻看书后的答案,方程的解是x=9,请问这个被污染的常数是( )
A.1 B.2 C.3 D.4
6.如果关于的不等式组有且只有个整数解,且关于的方程的解为非负整数,则符合条件的所有整数的和为( )
A.2 B.3 C.4 D.5
7.方程 =﹣ x+3的解为( )
A.x=4 B.x= C.x=﹣4 D.x=
8.如果关于的方程有非负整数解,且关于y的不等式组的解集为,则所有符合条件的整数的和为( ).
A.-7 B.-8 C. D.
9.把方程 去分母正确的是( )
A. B.
C. D.
10.已知一元一次方程 ,则下列解方程的过程正确的是( )
A.去分母,得
B.去分母,得
C.去分母,去括号,得
D.去分母,去括号,得
二、填空题
11.小林在解方程去分母时,方程右边的漏乘了6,因而求得方程的解为,由此可知a的值为 ,原方程的正确解为 .
12.方程 的解是 ,则关于x的方程 的解为 .
13.定义运算法则:例如:3 2=32+3×2=15.若2 x=10,则x的值为 .
14.如图所示的框图表示解方程3﹣5x=4﹣2x的流程,其中“系数化为1”这一步骤的依据是
15.写出一个关于x的一元一次方程,使它的解为x=5: .
16.已知关于x的方程,该方程的解为,则关于y的方程的解为 .
三、计算题
17.解下列一元一次方程:
(1)3x-2=1+2x
(2)
四、解答题
18. 老师在黑板上山了一道解方程的题,小明马上举手,要求到黑板上做,他是这样做的:
…...①
…...②
…...③
…...④
…...⑤
老师说:小明解一元一次方程的一般步骤都知道却没有掌握好,因此解题时有一步出现了错误.请你指出他错在第 ▲ 步,错误的原因是 ▲ .然后,请你自己细心地解此方程.
19.定义:如果两个一元一次方程的解之和为0,我们就称这两个方程为“友好方程”.例如:方程和为“友好方程”.
(1)请判断方程与方程是否为“友好方程”,并说明理由;
(2)若关于x的方程与方程是“友好方程”,求a的值.
20.小明解方程时,由于粗心大意,在去分母时,方程左边的1没有乘以10,由此求得的解为,试求a的值,并符合题意求出方程的解.
21.当k为何值时,关于x的方程7k+6x=2的解比关于x的方程2(x-8)+5=1-x的解大6?
22.已知关于x的方程ax=b有两个不同的解x1,和x2,求证这个方程必有无数多个解.
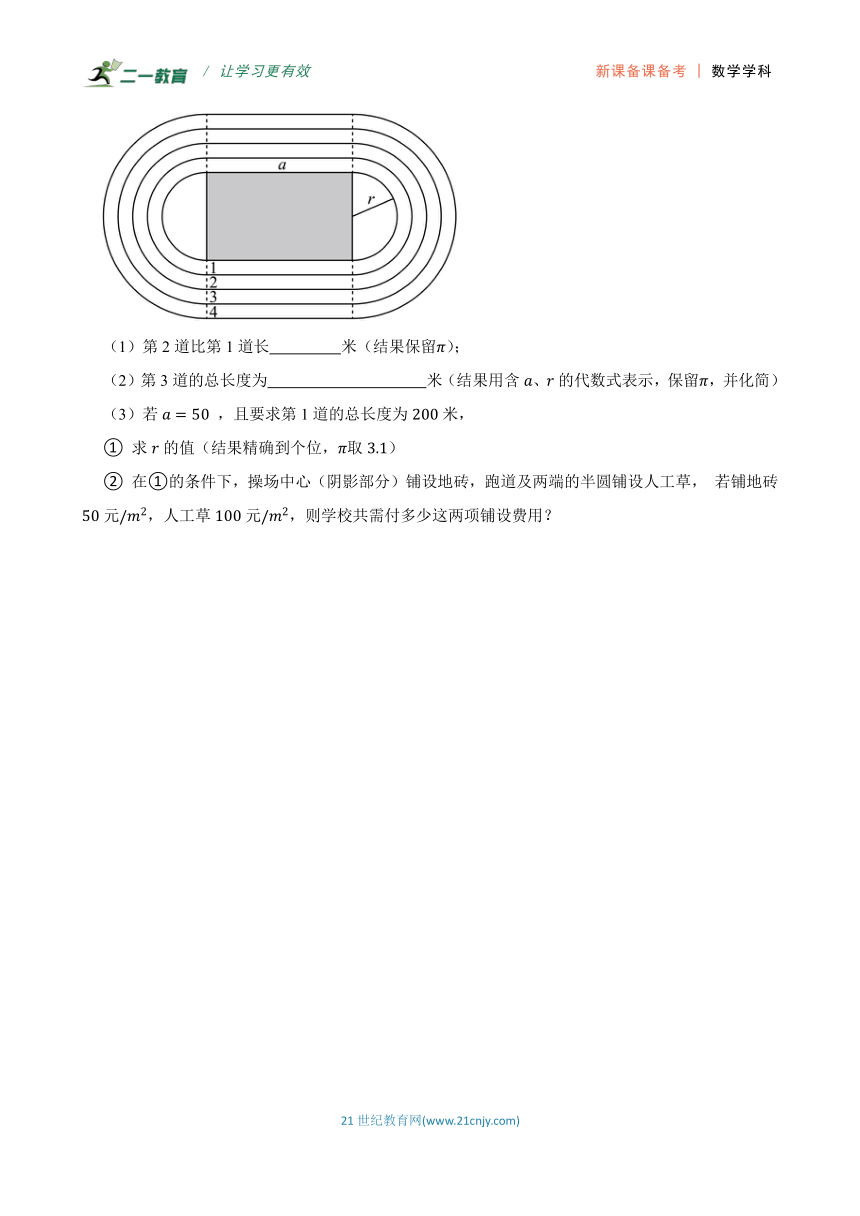
23.如图是某校田径运动场的平面图,最中间是长方形,长为米,两端为两个半圆,半径为米,每条跑道的宽为米,共四个跑道.若每个跑道按内侧边线的总长度计算路程,请解答下列问题:
(1)第2道比第1道长 米(结果保留);
(2)第3道的总长度为 米(结果用含、的代数式表示,保留,并化简)
(3)若 ,且要求第1道的总长度为米,
① 求的值(结果精确到个位,取)
② 在①的条件下,操场中心(阴影部分)铺设地砖,跑道及两端的半圆铺设人工草, 若铺地砖元,人工草元,则学校共需付多少这两项铺设费用?
参考答案及试题解析
1.C
2.B
3.D
4.D
5.B
【解答】解:设被污染的数字为y.
将x=9代入得:2×6﹣y=10.
解得:y=2.
故答案为:B.
【分析】设被污染的数字为y,将x=9代入,得到关于y的方程,从而可求得y的值.
6.B
7.A
【解答】解:去分母得:x=﹣2x+12,
解得:x=4,
故选A
【分析】方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
8.C
9.A
【解答】首先确定最简公分母为6,方程两边同时乘以6,得18x+2(2x-1)=18-3(x+1).
故选:A.
【分析】先确定最简公分母,再在方程两边同时乘以6(方程左边的3x和右边的3不能漏乘),分子是多项式的要加括号。即可得出答案。
10.C
【解答】原式等号左右同乘2去分母,得 ,所以A,B不符合题意;原式去分母去括号后应是 ,所以D不符合题意,
故答案为:C.
【分析】先找公分母,再去分母,然后去括号即可。
11.;
12.x=3
【解答】解: 方程 的解是 ,
关于x的方程 为:
故答案为:x=3
【分析】先求出再求出最后计算求解即可。
13.3
【解答】解:由题意,22+2x=10,解得x=3,
故答案为3.
【分析】根据新定义的运算法则得到22+2x=10,再解方程即可.
14.等式的性质
【解答】“系数化为1”这一步骤的依据是等式的性质,
故答案为:等式的性质
【分析】等式的性质,等号两边同时乘以未知数系数的倒数,等号不变.
15.x+1=6
【解答】
解:根据题意得:x+1=6.
故答案为:x+1=6.
【分析】按要求写出关于x的一元一次方程,求解即可。
16.
17.(1)解:移项,得3x-2x=1+2
合并同类项,得x=3
(2)解:去分母,得3(x-1)-6x=2(2-x)
去括号,得3x-3-6x=4-2x
移项,得3x-6x+2x=4+3
合并同类项,得-x=7
系数化为1,得x=-7
【分析】(1)根据解一元一次方程的解法:移项——合并同类项,解之即可得出答案.
(2)根据解一元一次方程的解法:去分母——去括号——移项——合并同类项——系数化为1,解之即可得出答案.
18.解:①;去分母时,1没有乘以各分母的最小公倍数12
【分析】本题考查解带有分数系数的一元一次方程,明确此类方程的解题步骤是关键。先去分母,再移项,合并同类项,系数化1,求解即可。
19.(1)解:方程的解为,方程的解为,
因为,
所以它们为“友好方程”;
(2)解:方程的解为,因为关于x的方程与方程是“友好方程”,
所以关于x的方程的解为,
所以把代入方程,
解得.
【分析】(1)先解方程得到两个方程的解,然后根据“友好方程”的定义判断解题;
(2)先求出方程的解,然后根据“友好方程”的定义代入的解,即可求出a的值解题.
(1)解:方程的解为,
方程的解为,
因为,
所以它们为“友好方程”;
(2)解:方程的解为,
因为关于x的方程与方程是“友好方程”,
所以关于x的方程的解为,
所以把代入方程,
解得.
20.解:∵去分母时,方程左边的1没有乘以10,
∴,
∵此时解得,
∴,
解得:,
∴原方程为:,
去分母可得:,
去括号可得:,
移项、化简可得:,
解得:,
∴,原方程的解为:.
【分析】先根据错误的计算方法求出a的值,再将a的值代入方程可得,再去分母,然后去括号,接着移项、合并同类项,最后系数化为1即可。
21.解:
【解答】解:解方程,得,
解方程,得,
∵关于x的方程的解比关于x的方程的解大6
∴,
解得:.
【分析】先解每个一元一次方程,根据两个方程解的关系建立k的方程,求解即可。
22.证明:因为x1、x2都是方程ax=b的解,所以
从而 即
又因为 ,所以必有a=0,因此
由于a=0且b=0,因此方程ax=b有无数多解
又解 ,方程 有唯一解 ,现在方程ax=b有两个不同的解,所以必有a=0从而
由于a=0,b=0,因此任一个数都是 的解
【分析】在 ,方程 有唯一解 ,
在a=0且b=0时,方程ax=b有无穷多解,x可为任意数
在a=0且 ,方程 无解.
根据一元一次方程的解得意义,可将和代入方程得:a=a=b,则a(-)=0,由题意关于x的方程ax=b有两个不同的解,即≠,所以必有a=0=b,因此方程ax=b有无数多解。
23.(1)
(2)
(3)解:①由题意得:,
∵,结果精确到个位,取
∴2×50+2×3.1r=200
解得:.
②由题意得:
铺地砖费用(元);
铺人工草费用元;
∴.4(元);
所以学校共需付这两项铺设费用为.4元
【解答】:解:(1)依题意,最中间是长方形,长为米,两端为两个半圆,半径为米,每条跑道的宽为米,
∴第1道的总长度为:米,
第2道的总长度为:米,
故(米),
故答案为:.
(2)由题意得:第3道的总长度为:米,
故答案为:
【分析】(1)根据题意表示出第2跑道和第1跑道的长,两者相减即可;两侧的两个半圆可以按一个整圆来计算周长;
(2)根据题意计算第3跑道的长:两个长方形的长+一个半径为(r+1.2×2)的圆,如此即可求出第3跑道长;
(3)①根据=200,代入a=50,π=3.1,解方程即可;
②先计算出长方形的面积,于是可得铺地砖的花费;再计算周围跑道的面积:两个长为a宽为1.2×4的长方形跑道面积+半径为(r+1.2×4)的圆面积.之后可得跑道铺人工草的花费,两个花费求和即可.
21世纪教育网(www.21cnjy.com)
2025-2026学年七年级上册数学单元考点培优湘教版(2024)
第3章 一次方程(组) 3.3 一元一次方程的解法
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若、表示非零常数,整式的值随的取值而发生变化,如下表,则关于的一元一次方程的解为( )
0 1 3 ……
1 3 5 9 ……
A. B. C. D.
2.把方程去分母后,正确的结果是( )
A. B.
C. D.
3.在解方程时,去括号正确的是( )
A. B.
C. D.
4.下列解方程中变形正确的有( )
①变形为;②变形为;③变形为;④变形为;⑤变形为.
A.①②④ B.②③④ C.①③⑤ D.②④⑤
5.小马虎做作业时,不小心将方程中的一个常数污染了,被污染的方程是2(x-3)-■=x+1,怎么办呢?他想了想,便翻看书后的答案,方程的解是x=9,请问这个被污染的常数是( )
A.1 B.2 C.3 D.4
6.如果关于的不等式组有且只有个整数解,且关于的方程的解为非负整数,则符合条件的所有整数的和为( )
A.2 B.3 C.4 D.5
7.方程 =﹣ x+3的解为( )
A.x=4 B.x= C.x=﹣4 D.x=
8.如果关于的方程有非负整数解,且关于y的不等式组的解集为,则所有符合条件的整数的和为( ).
A.-7 B.-8 C. D.
9.把方程 去分母正确的是( )
A. B.
C. D.
10.已知一元一次方程 ,则下列解方程的过程正确的是( )
A.去分母,得
B.去分母,得
C.去分母,去括号,得
D.去分母,去括号,得
二、填空题
11.小林在解方程去分母时,方程右边的漏乘了6,因而求得方程的解为,由此可知a的值为 ,原方程的正确解为 .
12.方程 的解是 ,则关于x的方程 的解为 .
13.定义运算法则:例如:3 2=32+3×2=15.若2 x=10,则x的值为 .
14.如图所示的框图表示解方程3﹣5x=4﹣2x的流程,其中“系数化为1”这一步骤的依据是
15.写出一个关于x的一元一次方程,使它的解为x=5: .
16.已知关于x的方程,该方程的解为,则关于y的方程的解为 .
三、计算题
17.解下列一元一次方程:
(1)3x-2=1+2x
(2)
四、解答题
18. 老师在黑板上山了一道解方程的题,小明马上举手,要求到黑板上做,他是这样做的:
…...①
…...②
…...③
…...④
…...⑤
老师说:小明解一元一次方程的一般步骤都知道却没有掌握好,因此解题时有一步出现了错误.请你指出他错在第 ▲ 步,错误的原因是 ▲ .然后,请你自己细心地解此方程.
19.定义:如果两个一元一次方程的解之和为0,我们就称这两个方程为“友好方程”.例如:方程和为“友好方程”.
(1)请判断方程与方程是否为“友好方程”,并说明理由;
(2)若关于x的方程与方程是“友好方程”,求a的值.
20.小明解方程时,由于粗心大意,在去分母时,方程左边的1没有乘以10,由此求得的解为,试求a的值,并符合题意求出方程的解.
21.当k为何值时,关于x的方程7k+6x=2的解比关于x的方程2(x-8)+5=1-x的解大6?
22.已知关于x的方程ax=b有两个不同的解x1,和x2,求证这个方程必有无数多个解.
23.如图是某校田径运动场的平面图,最中间是长方形,长为米,两端为两个半圆,半径为米,每条跑道的宽为米,共四个跑道.若每个跑道按内侧边线的总长度计算路程,请解答下列问题:
(1)第2道比第1道长 米(结果保留);
(2)第3道的总长度为 米(结果用含、的代数式表示,保留,并化简)
(3)若 ,且要求第1道的总长度为米,
① 求的值(结果精确到个位,取)
② 在①的条件下,操场中心(阴影部分)铺设地砖,跑道及两端的半圆铺设人工草, 若铺地砖元,人工草元,则学校共需付多少这两项铺设费用?
参考答案及试题解析
1.C
2.B
3.D
4.D
5.B
【解答】解:设被污染的数字为y.
将x=9代入得:2×6﹣y=10.
解得:y=2.
故答案为:B.
【分析】设被污染的数字为y,将x=9代入,得到关于y的方程,从而可求得y的值.
6.B
7.A
【解答】解:去分母得:x=﹣2x+12,
解得:x=4,
故选A
【分析】方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
8.C
9.A
【解答】首先确定最简公分母为6,方程两边同时乘以6,得18x+2(2x-1)=18-3(x+1).
故选:A.
【分析】先确定最简公分母,再在方程两边同时乘以6(方程左边的3x和右边的3不能漏乘),分子是多项式的要加括号。即可得出答案。
10.C
【解答】原式等号左右同乘2去分母,得 ,所以A,B不符合题意;原式去分母去括号后应是 ,所以D不符合题意,
故答案为:C.
【分析】先找公分母,再去分母,然后去括号即可。
11.;
12.x=3
【解答】解: 方程 的解是 ,
关于x的方程 为:
故答案为:x=3
【分析】先求出再求出最后计算求解即可。
13.3
【解答】解:由题意,22+2x=10,解得x=3,
故答案为3.
【分析】根据新定义的运算法则得到22+2x=10,再解方程即可.
14.等式的性质
【解答】“系数化为1”这一步骤的依据是等式的性质,
故答案为:等式的性质
【分析】等式的性质,等号两边同时乘以未知数系数的倒数,等号不变.
15.x+1=6
【解答】
解:根据题意得:x+1=6.
故答案为:x+1=6.
【分析】按要求写出关于x的一元一次方程,求解即可。
16.
17.(1)解:移项,得3x-2x=1+2
合并同类项,得x=3
(2)解:去分母,得3(x-1)-6x=2(2-x)
去括号,得3x-3-6x=4-2x
移项,得3x-6x+2x=4+3
合并同类项,得-x=7
系数化为1,得x=-7
【分析】(1)根据解一元一次方程的解法:移项——合并同类项,解之即可得出答案.
(2)根据解一元一次方程的解法:去分母——去括号——移项——合并同类项——系数化为1,解之即可得出答案.
18.解:①;去分母时,1没有乘以各分母的最小公倍数12
【分析】本题考查解带有分数系数的一元一次方程,明确此类方程的解题步骤是关键。先去分母,再移项,合并同类项,系数化1,求解即可。
19.(1)解:方程的解为,方程的解为,
因为,
所以它们为“友好方程”;
(2)解:方程的解为,因为关于x的方程与方程是“友好方程”,
所以关于x的方程的解为,
所以把代入方程,
解得.
【分析】(1)先解方程得到两个方程的解,然后根据“友好方程”的定义判断解题;
(2)先求出方程的解,然后根据“友好方程”的定义代入的解,即可求出a的值解题.
(1)解:方程的解为,
方程的解为,
因为,
所以它们为“友好方程”;
(2)解:方程的解为,
因为关于x的方程与方程是“友好方程”,
所以关于x的方程的解为,
所以把代入方程,
解得.
20.解:∵去分母时,方程左边的1没有乘以10,
∴,
∵此时解得,
∴,
解得:,
∴原方程为:,
去分母可得:,
去括号可得:,
移项、化简可得:,
解得:,
∴,原方程的解为:.
【分析】先根据错误的计算方法求出a的值,再将a的值代入方程可得,再去分母,然后去括号,接着移项、合并同类项,最后系数化为1即可。
21.解:
【解答】解:解方程,得,
解方程,得,
∵关于x的方程的解比关于x的方程的解大6
∴,
解得:.
【分析】先解每个一元一次方程,根据两个方程解的关系建立k的方程,求解即可。
22.证明:因为x1、x2都是方程ax=b的解,所以
从而 即
又因为 ,所以必有a=0,因此
由于a=0且b=0,因此方程ax=b有无数多解
又解 ,方程 有唯一解 ,现在方程ax=b有两个不同的解,所以必有a=0从而
由于a=0,b=0,因此任一个数都是 的解
【分析】在 ,方程 有唯一解 ,
在a=0且b=0时,方程ax=b有无穷多解,x可为任意数
在a=0且 ,方程 无解.
根据一元一次方程的解得意义,可将和代入方程得:a=a=b,则a(-)=0,由题意关于x的方程ax=b有两个不同的解,即≠,所以必有a=0=b,因此方程ax=b有无数多解。
23.(1)
(2)
(3)解:①由题意得:,
∵,结果精确到个位,取
∴2×50+2×3.1r=200
解得:.
②由题意得:
铺地砖费用(元);
铺人工草费用元;
∴.4(元);
所以学校共需付这两项铺设费用为.4元
【解答】:解:(1)依题意,最中间是长方形,长为米,两端为两个半圆,半径为米,每条跑道的宽为米,
∴第1道的总长度为:米,
第2道的总长度为:米,
故(米),
故答案为:.
(2)由题意得:第3道的总长度为:米,
故答案为:
【分析】(1)根据题意表示出第2跑道和第1跑道的长,两者相减即可;两侧的两个半圆可以按一个整圆来计算周长;
(2)根据题意计算第3跑道的长:两个长方形的长+一个半径为(r+1.2×2)的圆,如此即可求出第3跑道长;
(3)①根据=200,代入a=50,π=3.1,解方程即可;
②先计算出长方形的面积,于是可得铺地砖的花费;再计算周围跑道的面积:两个长为a宽为1.2×4的长方形跑道面积+半径为(r+1.2×4)的圆面积.之后可得跑道铺人工草的花费,两个花费求和即可.
21世纪教育网(www.21cnjy.com)
同课章节目录
