【章节考点培优】3.4一元一次方程的应用-2025-2026学年七年级上册数学湘教版(2024)(含答案解析)
文档属性
| 名称 | 【章节考点培优】3.4一元一次方程的应用-2025-2026学年七年级上册数学湘教版(2024)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 180.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 21:30:56 | ||
图片预览



文档简介
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年七年级上册数学单元考点培优湘教版(2024)
第3章 一次方程(组) 3.4 一元一次方程的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,三块形状完全相同的小长方形可以拼成一个大长方形.若大长方形的周长为,则大长方形的面积是( )
A. B. C. D.
2.《九章算术》是我国古代数学名著,书中出现了一个“共买鸡问题”,原文是:今有人共买鸡,人出九钱,盈十一钱;人出六钱,不足十六钱,问人数、物价各几何?设买鸡的人数为人,则下面符合题意的方程是( )
A. B.
C. D.
3.某铁路桥长m,一列火车匀速行驶从桥上通过,测得该火车从开始上桥到完全过桥共用了,火车的速度为,则火车的长度为( )
A.m B.m C.m D.m
4.我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹.每人六竿多十四,每人八竿恰齐足.”其大意是:牧童们在树下拿着竹竿高兴地玩耍,不知有多少人和竹竿.每人6竿,多14竿;每人8竿,恰好用完.若设牧童有x人,根据题意可列方程为( )
A. B. C. D.
5.某商场购进一批服装,每件进价为100元,由于换季滞销,商场决定将这种服装按标价的7折销售,若打折后每件服装仍能获利,设该服装的标价为元,根据题意可列方程( )
A. B.
C. D.
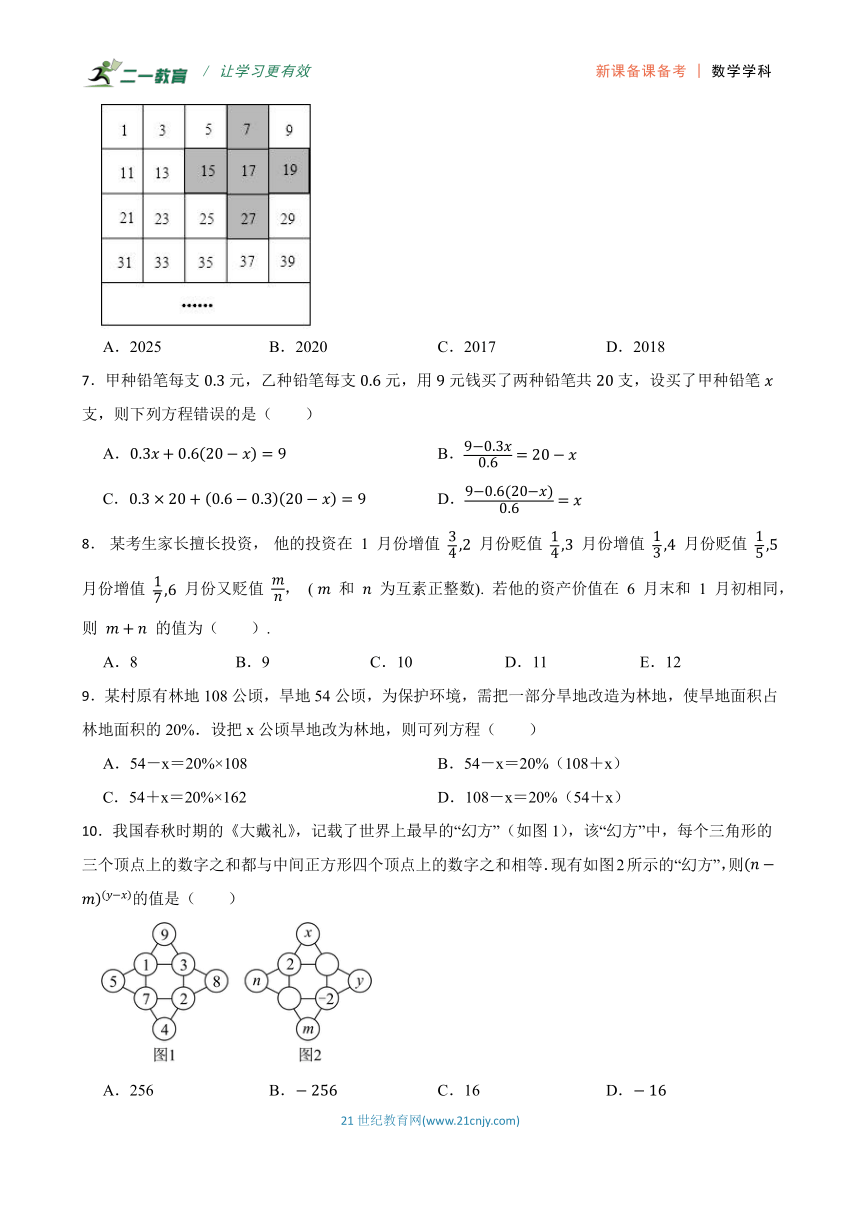
6.将连续的奇数1,3,5,7,9,…排成如图所示的数表,若阴影十字框上下左右移动,则阴影十字框中的五个数字之和可以是( )
A.2025 B.2020 C.2017 D.2018
7.甲种铅笔每支元,乙种铅笔每支元,用元钱买了两种铅笔共支,设买了甲种铅笔支,则下列方程错误的是( )
A. B.
C. D.
8. 某考生家长擅长投资, 他的投资在 1 月份增值 月份贬值 月份增值 月份贬值 月份增值 月份又贬值 , ( 和 为互素正整数). 若他的资产价值在 6 月末和 1 月初相同, 则 的值为( ).
A.8 B.9 C.10 D.11 E.12
9.某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程( )
A.54-x=20%×108 B.54-x=20%(108+x)
C.54+x=20%×162 D.108-x=20%(54+x)
10.我国春秋时期的《大戴礼》,记载了世界上最早的“幻方”(如图1),该“幻方”中,每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.现有如图2所示的“幻方”,则的值是( )
A.256 B. C.16 D.
二、填空题
11.在“双减”政策下,我校开展了丰富多彩的兴趣小组和社团活动.活动中小民邀请小刚玩“你想我猜”的游戏,游戏规则是:
第一步:请小刚在心中想一个喜欢的数字,并记住这个数字;
第二步:把喜欢的数字乘以2再加上6,得到一个新的数;
第三步:把新得到的数除以2,写在纸条上交给小民.
小民打开纸条看到数字6,马上就猜出了小刚喜欢的数,这个数是 .
12.几个人共同种一批树苗,如果每人种10棵,则剩下6棵树苗未种,如果每人种12棵,则缺6棵树苗,用x表示参加种树的人数,则可列出一元一次方程 .
13.小明爸爸存了年利率为2.25%的一年期定期储蓄,一年到期后将交纳利息税72元(利息税率为利息的20%),则小明爸爸存入的人民币为 元.
14.足球的表面由白块和黑块组成.已知黑块是五边形,白块是六边形,且每一白块的6条边中,有3边与黑块相接,另3边与白块相接,每一黑块的5边全与白块的边相接,已知足球表面的黑块总数是12,则白块数为 .
15.七年级(2)班有46人报名参加文学社或书画社.已知参加文学社的人数比参加书画社的人数多10人,两社都参加的有20人,则参加书画社的有 人.
16.如图,在三角形中,,点从点出发,沿折线以每秒个单位长度的速度向终点运动.点从点出发,沿折线以每秒个单位长度的速度运动.两点同时出发,点停止时,点也随之停止.设点运动的时间为秒.当时,则的值为 .
三、计算题
17.为满足不同学生个性化课后服务需求,助力“双减”政策落地生根,某初中开展了丰富多彩的小组活动.下表是几位同学某学期参加的课外兴趣小组活动时间统计表,其中同一兴趣小组每次活动时间相同:
参与小组活动总时间/h 科技小组活动次数 体育小组活动次数
小新 20.5 7 5
王华 19 6 5
小晴 8.5
(1)科技小组每次活动的时间为______h,体育小组每次活动的时间为______h(直接写出答案);
(2)在一次聊天中,小杰说他参加科技小组和体育小组活动共14次,且参加科技小组的活动时长刚好是参加体育小组活动时长的两倍.请你通过计算,判断小杰的话是否属实;
(3)小晴共参加小组活动______次(直接写出答案)
四、解答题
18.某校七年级学生在数学课上进行了项目化学习研究,某学习兴趣小组研究如下:
【提出驱动性问题】商品优惠问题
【设计实践性任务】选择“素材1”“素材2”设计了“任务1”“任务2”“任务3”的实践活动.
探究商品优惠问题
素材 素材1 两商场以同样的价格出售篮球运动服和篮球两种商品,已知每套篮球运动服比篮球贵元.
素材2 已知套篮球运动服比个篮球贵元.
任务 任务1 求一个篮球和一套篮球运动服的单价?
任务2 为了促销两商场推出优惠活动: 商场:每购买满套篮球队服,送一个篮球; 商场:原价购买篮球队服,篮球的价格打八折,若需要购买篮球个和篮球运动服套. 请你用含的代数式表示在两个商场所需要花费的费用?
任务3 学习兴趣小组通过调查,两家商场在促销两种商品优惠活动中,因购买数量不同,花费的费用也不同,请你帮兴趣小组提出一个比较划算的购买方案?
请你根据以上提供的信息,帮学习兴趣小组解决相关问题?
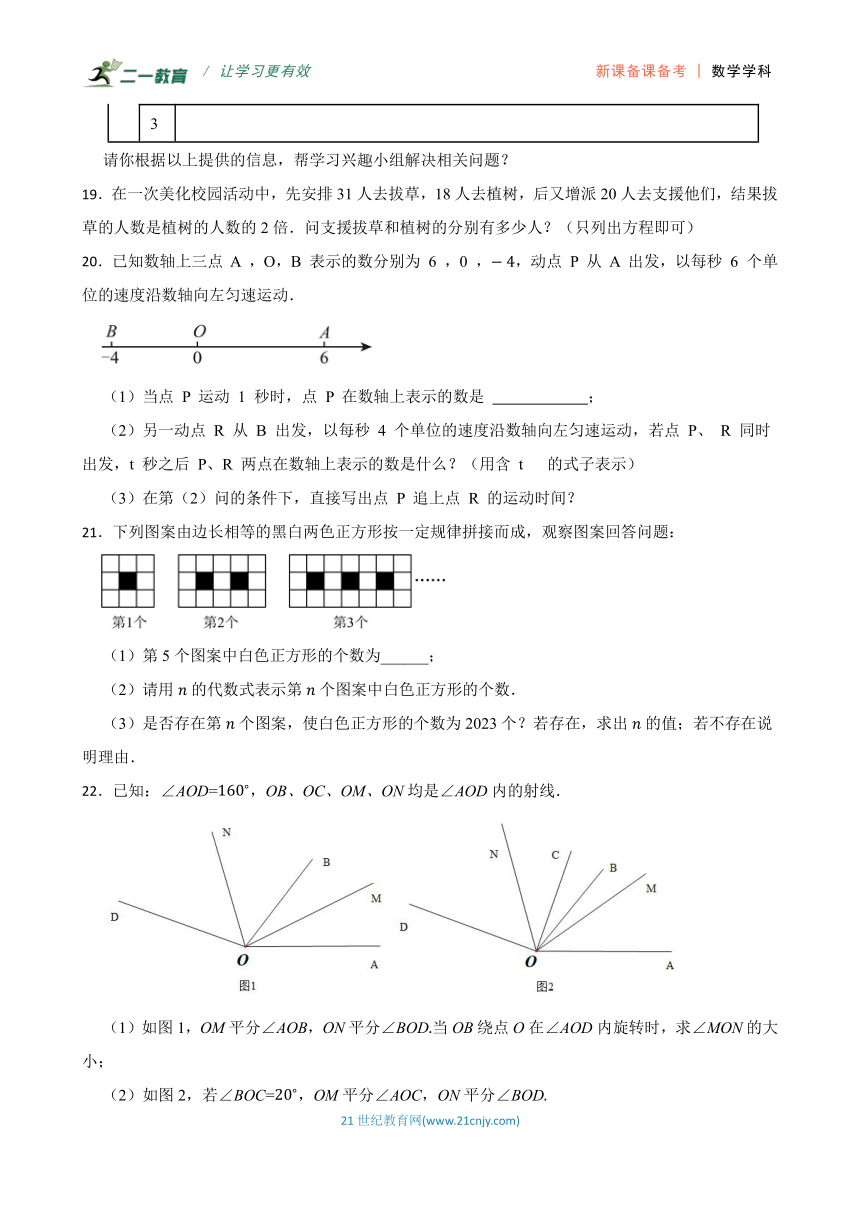
19.在一次美化校园活动中,先安排31人去拔草,18人去植树,后又增派20人去支援他们,结果拔草的人数是植树的人数的2倍.问支援拔草和植树的分别有多少人?(只列出方程即可)
20.已知数轴上三点 A ,O,B 表示的数分别为 6 ,0 ,,动点 P 从 A 出发,以每秒 6 个单位的速度沿数轴向左匀速运动.
(1)当点 P 运动 1 秒时,点 P 在数轴上表示的数是 ;
(2)另一动点 R 从 B 出发,以每秒 4 个单位的速度沿数轴向左匀速运动,若点 P、 R 同时出发,t 秒之后 P、R 两点在数轴上表示的数是什么?(用含 t 的式子表示)
(3)在第(2)问的条件下,直接写出点 P 追上点 R 的运动时间?
21.下列图案由边长相等的黑白两色正方形按一定规律拼接而成,观察图案回答问题:
(1)第5个图案中白色正方形的个数为______;
(2)请用的代数式表示第个图案中白色正方形的个数.
(3)是否存在第个图案,使白色正方形的个数为2023个?若存在,求出的值;若不存在说明理由.
22.已知:∠AOD=,OB、OC、OM、ON均是∠AOD内的射线.
(1)如图1,OM平分∠AOB,ON平分∠BOD当OB绕点O在∠AOD内旋转时,求∠MON的大小;
(2)如图2,若∠BOC=,OM平分∠AOC,ON平分∠BOD
①当∠BOC绕点O在∠AOD内旋转时求∠MON的大小;
②若∠AOB=,当∠BOC在∠AOD内绕着点O以每秒的速度逆时针旋转t秒时,∠AOM:∠DON=2:3,求此时t的值.
23.在数轴上O为数轴的原点,点A、B在数轴上对应的数分别表示为a、b,且、4为最大负整数,.
(1) , .
(2)如图1,数轴上有一点M,若点M到点B的距离是点M到点A的距离的3倍,求点M在数轴上表示的数.
(3)如图2,在数轴上有两个动点P、Q,点P、Q同时分别从A、B出发沿数轴正方向运动,点P的运动速度为m个单位长度/秒,点Q的运动速度为n个单位长度/秒,取线段的中点为点C,在运动过程中,若线段的长度为固定的值,直接写出m与n的数量关系.
参考答案及试题解析
1.D
2.B
3.B
4.A
5.A
【解答】解:设该服装每件的标价是x元,根据题意得:
,
故答案为:A.
【分析】设该服装每件的标价是x元,根据利润售价进价可列关于x的方程,解方程即可求解.
6.A
【解答】解:设阴影十字框中间的数为x,则十字框中的五个数的和:x+(x﹣10)+(x+10)+(x﹣2)(x+2)=5x,
A、2025÷5=405,在第三列,符合题意;
B、2020÷5=404,数表中都是奇数,不符合题意;
C、2017÷5=403.4,数表中都是奇数,不符合题意;
D、2018÷5=403.6,数表中都是奇数,不符合题意;
故选A.
【分析】设阴影十字框中间的数为x,得到其余4个数的代数式,把这5个数相加,可得和为5x,再逐一分析各选项中的数即可.
7.D
【解答】解:设买了甲种铅笔x支,则买了乙种铅笔(20-x)支,根据题意得:0.3x+0.6(20-x)=9,
,
可得,
所以.
故选:D.
【分析】本题考查了由实际问题抽象出一元一次方程,设买了甲种铅笔x支,得到买了乙种铅笔(20-x)支,结合总价=单价×数量,得出A选项中方程,再由(总价-购买甲种铅笔所花费用)÷甲种铅笔的单价=购买甲种铅笔的数量可得出B选项中方程,由0.3×购买铅笔总数量+(乙种铅笔比甲种铅笔高出的单价)×乙种铅笔购买数量=总费用可得出选项C中方程,得到答案.
8.D
【解答】解:设1月初资产价值为x,根据题意可得:
解得:,
∵ 和 为互素正整数 ,
∴m=3,n=8,m+n=11.
故答案为:D.
【分析】设1月初资产价值为x,根据题意列出等式,即可求解.
9.B
【解答】设把x公顷旱地改为林地,根据题意可得方程:54-x=20%(108+x).
故选B.
【分析】设把x公顷旱地改为林地,根据旱地面积占林地面积的20%列出方程即可.
10.A
【解答】解:根据题意可知:,
解得:,
所以,,
故答案为:A.
【分析】根据题意列出方程,然后求出的值,再整体代入计算即可.
11.3
【解答】解:设小刚心里想的数字是x,
第二步结果:
第三步结果:
∴ ,解得
故答案为:3.
【分析】设小刚心里想的数字是x,则第二步的结果为2x+6,第三步的结果为(2x+6)÷2=x+3,然后结合最后的结果为6列出方程,求解即可.
12.10x+6=12x-6
【解答】解:设参与种树的人数为x人.
则10x+6=12x-6,
故答案为:10x+6=12x-6
【分析】由参与种树的人数为x人,分别用“每人种10棵,则剩下6棵树苗未种;如果每人种12棵,则缺6棵树苗”表示出树苗总棵树列方程即可.
13.16000
【解答】解:设小明爸爸存入的人民币为x元.
根据题意得:2.25%×20%x=72,
解得:x=16000.
则小明爸爸存入的人民币为16000元.
故答案为:16000
【分析】此题的等量关系为:本金×年利率×利息税率=72,设未知数列方程,求解即可。
14.20
15.28
【解答】解:设参加书画社的有x人,根据题意得:
(46+20﹣x)﹣x=10,
解得:x=28,
故答案为:28.
【分析】设参加书画社的有x人,则参加文学社的有46+20﹣x人,根据参加文学社的人数比参加书画社的人数多10人列方程求解.
16.或
【解答】解:当点在边上,点在边上时,,如图,
∵,
∴为等边三角形,,
∵,
∴,
∴,
∴,
解得;
当点都在边上时,,如图,
同理可得,
∴,
∴,
解得;
∴或,
故答案为:或.
【分析】分情况讨论: 当点在边上,点在边上时, ,根据等边三角形判定定理可得为等边三角形,, 则 ,再根据含30°角的直角三角形性质列出方程,解方程可得t, 当点都在边上时, , 同理可得, 再根据含30°角的直角三角形性质列出方程,解方程可得t.
17.(1),
(2)不属实
(3)
18.任务一:一个篮球的单价为元,一套篮球运动服的单价为元;任务二:商场所需要花费的费用为:若,所需要花费的费用为元;若,所需要花费的费用为元;商场费用为元;任务三:若,且为整数,则选择商场比较划算;若,选择商场费用一样;若,且为整数;则选择商场比较划算
19.解:设支援拔草的有x人,由题意得:
31+x=2[18+(20﹣x)].
【分析】首先设支援拔草的有x人,则支援植树的有(20﹣x)人,根据题意可得等量关系:原来拔草人数+支援拔草的人数=2×(原来植树的人数+支援植树的人数).
20.(1)
(2),
(3)
21.(1)28
(2)
(3)存在,
22.(1)解:∵ OM平分∠AOB,ON平分∠BOD ,
∴ ∠BOM=∠BOA,∠BON=∠BOD,
∴ ∠MON=∠BOM+∠BON=(∠BOA+∠BOD)=∠AOD=80°.
(2)解: ①∵ OM 平分∠AOC,ON 平分∠BOD,
∴ ∠AOM=∠COM=∠AOC,∠DON=∠BON=∠BOD,
∵ ∠BOC=∠AOC+∠BOD-∠AOD=20°,
∴ ∠AOC+∠BOD=180°,
∴ ∠AOM+∠DON=(∠AOC+∠BOD)=90°,
∴ ∠MON=∠AOD-(∠AOM+∠DON)=160°-90°=70°;
②∵ ∠BOC在∠AOD内绕着点O以每秒的速度逆时针旋转t,∠BOC=20°,
∴ ∠AOC=∠AOB+∠BOC=10°+20°+t°=30°+t°,
∵ OM平分∠AOC,
∴ ∠AOM=∠AOC=15°+t°,
∵ ∠BOD=∠AOD-∠AOB=160°-(10°+t°)=150°-t,
∵ ON平分∠BOD,
∴ ∠DON=∠BOD=75°-t°,
∵ ∠AOM :∠DON=2:3 ,
∴ (15°+t°):(75°-t°)=2:3,
解得,t=42,
即t的值为42.
【分析】(1)根据角平分线的定义可得∠BOM=∠BOA,∠BON=∠BOD,即可求得;
(2) ① 根据角平分线的定义可得∠AOM=∠COM=∠AOC,∠DON=∠BON=∠BOD,根据∠BOC=∠AOC+∠BOD-∠AOD计算出∠AOC+∠BOD=180°,推出∠AOM+∠DON=90°,即可求得;
②根据角平分线的定义可得∠AOM=∠AOC=15°+t°,∠DON=∠BOD=75°-t°,再根据 ∠AOM:∠DON=2:3,列出方程,解方程即可求得.
23.(1),3
(2)或
(3)
21世纪教育网(www.21cnjy.com)
2025-2026学年七年级上册数学单元考点培优湘教版(2024)
第3章 一次方程(组) 3.4 一元一次方程的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,三块形状完全相同的小长方形可以拼成一个大长方形.若大长方形的周长为,则大长方形的面积是( )
A. B. C. D.
2.《九章算术》是我国古代数学名著,书中出现了一个“共买鸡问题”,原文是:今有人共买鸡,人出九钱,盈十一钱;人出六钱,不足十六钱,问人数、物价各几何?设买鸡的人数为人,则下面符合题意的方程是( )
A. B.
C. D.
3.某铁路桥长m,一列火车匀速行驶从桥上通过,测得该火车从开始上桥到完全过桥共用了,火车的速度为,则火车的长度为( )
A.m B.m C.m D.m
4.我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹.每人六竿多十四,每人八竿恰齐足.”其大意是:牧童们在树下拿着竹竿高兴地玩耍,不知有多少人和竹竿.每人6竿,多14竿;每人8竿,恰好用完.若设牧童有x人,根据题意可列方程为( )
A. B. C. D.
5.某商场购进一批服装,每件进价为100元,由于换季滞销,商场决定将这种服装按标价的7折销售,若打折后每件服装仍能获利,设该服装的标价为元,根据题意可列方程( )
A. B.
C. D.
6.将连续的奇数1,3,5,7,9,…排成如图所示的数表,若阴影十字框上下左右移动,则阴影十字框中的五个数字之和可以是( )
A.2025 B.2020 C.2017 D.2018
7.甲种铅笔每支元,乙种铅笔每支元,用元钱买了两种铅笔共支,设买了甲种铅笔支,则下列方程错误的是( )
A. B.
C. D.
8. 某考生家长擅长投资, 他的投资在 1 月份增值 月份贬值 月份增值 月份贬值 月份增值 月份又贬值 , ( 和 为互素正整数). 若他的资产价值在 6 月末和 1 月初相同, 则 的值为( ).
A.8 B.9 C.10 D.11 E.12
9.某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程( )
A.54-x=20%×108 B.54-x=20%(108+x)
C.54+x=20%×162 D.108-x=20%(54+x)
10.我国春秋时期的《大戴礼》,记载了世界上最早的“幻方”(如图1),该“幻方”中,每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.现有如图2所示的“幻方”,则的值是( )
A.256 B. C.16 D.
二、填空题
11.在“双减”政策下,我校开展了丰富多彩的兴趣小组和社团活动.活动中小民邀请小刚玩“你想我猜”的游戏,游戏规则是:
第一步:请小刚在心中想一个喜欢的数字,并记住这个数字;
第二步:把喜欢的数字乘以2再加上6,得到一个新的数;
第三步:把新得到的数除以2,写在纸条上交给小民.
小民打开纸条看到数字6,马上就猜出了小刚喜欢的数,这个数是 .
12.几个人共同种一批树苗,如果每人种10棵,则剩下6棵树苗未种,如果每人种12棵,则缺6棵树苗,用x表示参加种树的人数,则可列出一元一次方程 .
13.小明爸爸存了年利率为2.25%的一年期定期储蓄,一年到期后将交纳利息税72元(利息税率为利息的20%),则小明爸爸存入的人民币为 元.
14.足球的表面由白块和黑块组成.已知黑块是五边形,白块是六边形,且每一白块的6条边中,有3边与黑块相接,另3边与白块相接,每一黑块的5边全与白块的边相接,已知足球表面的黑块总数是12,则白块数为 .
15.七年级(2)班有46人报名参加文学社或书画社.已知参加文学社的人数比参加书画社的人数多10人,两社都参加的有20人,则参加书画社的有 人.
16.如图,在三角形中,,点从点出发,沿折线以每秒个单位长度的速度向终点运动.点从点出发,沿折线以每秒个单位长度的速度运动.两点同时出发,点停止时,点也随之停止.设点运动的时间为秒.当时,则的值为 .
三、计算题
17.为满足不同学生个性化课后服务需求,助力“双减”政策落地生根,某初中开展了丰富多彩的小组活动.下表是几位同学某学期参加的课外兴趣小组活动时间统计表,其中同一兴趣小组每次活动时间相同:
参与小组活动总时间/h 科技小组活动次数 体育小组活动次数
小新 20.5 7 5
王华 19 6 5
小晴 8.5
(1)科技小组每次活动的时间为______h,体育小组每次活动的时间为______h(直接写出答案);
(2)在一次聊天中,小杰说他参加科技小组和体育小组活动共14次,且参加科技小组的活动时长刚好是参加体育小组活动时长的两倍.请你通过计算,判断小杰的话是否属实;
(3)小晴共参加小组活动______次(直接写出答案)
四、解答题
18.某校七年级学生在数学课上进行了项目化学习研究,某学习兴趣小组研究如下:
【提出驱动性问题】商品优惠问题
【设计实践性任务】选择“素材1”“素材2”设计了“任务1”“任务2”“任务3”的实践活动.
探究商品优惠问题
素材 素材1 两商场以同样的价格出售篮球运动服和篮球两种商品,已知每套篮球运动服比篮球贵元.
素材2 已知套篮球运动服比个篮球贵元.
任务 任务1 求一个篮球和一套篮球运动服的单价?
任务2 为了促销两商场推出优惠活动: 商场:每购买满套篮球队服,送一个篮球; 商场:原价购买篮球队服,篮球的价格打八折,若需要购买篮球个和篮球运动服套. 请你用含的代数式表示在两个商场所需要花费的费用?
任务3 学习兴趣小组通过调查,两家商场在促销两种商品优惠活动中,因购买数量不同,花费的费用也不同,请你帮兴趣小组提出一个比较划算的购买方案?
请你根据以上提供的信息,帮学习兴趣小组解决相关问题?
19.在一次美化校园活动中,先安排31人去拔草,18人去植树,后又增派20人去支援他们,结果拔草的人数是植树的人数的2倍.问支援拔草和植树的分别有多少人?(只列出方程即可)
20.已知数轴上三点 A ,O,B 表示的数分别为 6 ,0 ,,动点 P 从 A 出发,以每秒 6 个单位的速度沿数轴向左匀速运动.
(1)当点 P 运动 1 秒时,点 P 在数轴上表示的数是 ;
(2)另一动点 R 从 B 出发,以每秒 4 个单位的速度沿数轴向左匀速运动,若点 P、 R 同时出发,t 秒之后 P、R 两点在数轴上表示的数是什么?(用含 t 的式子表示)
(3)在第(2)问的条件下,直接写出点 P 追上点 R 的运动时间?
21.下列图案由边长相等的黑白两色正方形按一定规律拼接而成,观察图案回答问题:
(1)第5个图案中白色正方形的个数为______;
(2)请用的代数式表示第个图案中白色正方形的个数.
(3)是否存在第个图案,使白色正方形的个数为2023个?若存在,求出的值;若不存在说明理由.
22.已知:∠AOD=,OB、OC、OM、ON均是∠AOD内的射线.
(1)如图1,OM平分∠AOB,ON平分∠BOD当OB绕点O在∠AOD内旋转时,求∠MON的大小;
(2)如图2,若∠BOC=,OM平分∠AOC,ON平分∠BOD
①当∠BOC绕点O在∠AOD内旋转时求∠MON的大小;
②若∠AOB=,当∠BOC在∠AOD内绕着点O以每秒的速度逆时针旋转t秒时,∠AOM:∠DON=2:3,求此时t的值.
23.在数轴上O为数轴的原点,点A、B在数轴上对应的数分别表示为a、b,且、4为最大负整数,.
(1) , .
(2)如图1,数轴上有一点M,若点M到点B的距离是点M到点A的距离的3倍,求点M在数轴上表示的数.
(3)如图2,在数轴上有两个动点P、Q,点P、Q同时分别从A、B出发沿数轴正方向运动,点P的运动速度为m个单位长度/秒,点Q的运动速度为n个单位长度/秒,取线段的中点为点C,在运动过程中,若线段的长度为固定的值,直接写出m与n的数量关系.
参考答案及试题解析
1.D
2.B
3.B
4.A
5.A
【解答】解:设该服装每件的标价是x元,根据题意得:
,
故答案为:A.
【分析】设该服装每件的标价是x元,根据利润售价进价可列关于x的方程,解方程即可求解.
6.A
【解答】解:设阴影十字框中间的数为x,则十字框中的五个数的和:x+(x﹣10)+(x+10)+(x﹣2)(x+2)=5x,
A、2025÷5=405,在第三列,符合题意;
B、2020÷5=404,数表中都是奇数,不符合题意;
C、2017÷5=403.4,数表中都是奇数,不符合题意;
D、2018÷5=403.6,数表中都是奇数,不符合题意;
故选A.
【分析】设阴影十字框中间的数为x,得到其余4个数的代数式,把这5个数相加,可得和为5x,再逐一分析各选项中的数即可.
7.D
【解答】解:设买了甲种铅笔x支,则买了乙种铅笔(20-x)支,根据题意得:0.3x+0.6(20-x)=9,
,
可得,
所以.
故选:D.
【分析】本题考查了由实际问题抽象出一元一次方程,设买了甲种铅笔x支,得到买了乙种铅笔(20-x)支,结合总价=单价×数量,得出A选项中方程,再由(总价-购买甲种铅笔所花费用)÷甲种铅笔的单价=购买甲种铅笔的数量可得出B选项中方程,由0.3×购买铅笔总数量+(乙种铅笔比甲种铅笔高出的单价)×乙种铅笔购买数量=总费用可得出选项C中方程,得到答案.
8.D
【解答】解:设1月初资产价值为x,根据题意可得:
解得:,
∵ 和 为互素正整数 ,
∴m=3,n=8,m+n=11.
故答案为:D.
【分析】设1月初资产价值为x,根据题意列出等式,即可求解.
9.B
【解答】设把x公顷旱地改为林地,根据题意可得方程:54-x=20%(108+x).
故选B.
【分析】设把x公顷旱地改为林地,根据旱地面积占林地面积的20%列出方程即可.
10.A
【解答】解:根据题意可知:,
解得:,
所以,,
故答案为:A.
【分析】根据题意列出方程,然后求出的值,再整体代入计算即可.
11.3
【解答】解:设小刚心里想的数字是x,
第二步结果:
第三步结果:
∴ ,解得
故答案为:3.
【分析】设小刚心里想的数字是x,则第二步的结果为2x+6,第三步的结果为(2x+6)÷2=x+3,然后结合最后的结果为6列出方程,求解即可.
12.10x+6=12x-6
【解答】解:设参与种树的人数为x人.
则10x+6=12x-6,
故答案为:10x+6=12x-6
【分析】由参与种树的人数为x人,分别用“每人种10棵,则剩下6棵树苗未种;如果每人种12棵,则缺6棵树苗”表示出树苗总棵树列方程即可.
13.16000
【解答】解:设小明爸爸存入的人民币为x元.
根据题意得:2.25%×20%x=72,
解得:x=16000.
则小明爸爸存入的人民币为16000元.
故答案为:16000
【分析】此题的等量关系为:本金×年利率×利息税率=72,设未知数列方程,求解即可。
14.20
15.28
【解答】解:设参加书画社的有x人,根据题意得:
(46+20﹣x)﹣x=10,
解得:x=28,
故答案为:28.
【分析】设参加书画社的有x人,则参加文学社的有46+20﹣x人,根据参加文学社的人数比参加书画社的人数多10人列方程求解.
16.或
【解答】解:当点在边上,点在边上时,,如图,
∵,
∴为等边三角形,,
∵,
∴,
∴,
∴,
解得;
当点都在边上时,,如图,
同理可得,
∴,
∴,
解得;
∴或,
故答案为:或.
【分析】分情况讨论: 当点在边上,点在边上时, ,根据等边三角形判定定理可得为等边三角形,, 则 ,再根据含30°角的直角三角形性质列出方程,解方程可得t, 当点都在边上时, , 同理可得, 再根据含30°角的直角三角形性质列出方程,解方程可得t.
17.(1),
(2)不属实
(3)
18.任务一:一个篮球的单价为元,一套篮球运动服的单价为元;任务二:商场所需要花费的费用为:若,所需要花费的费用为元;若,所需要花费的费用为元;商场费用为元;任务三:若,且为整数,则选择商场比较划算;若,选择商场费用一样;若,且为整数;则选择商场比较划算
19.解:设支援拔草的有x人,由题意得:
31+x=2[18+(20﹣x)].
【分析】首先设支援拔草的有x人,则支援植树的有(20﹣x)人,根据题意可得等量关系:原来拔草人数+支援拔草的人数=2×(原来植树的人数+支援植树的人数).
20.(1)
(2),
(3)
21.(1)28
(2)
(3)存在,
22.(1)解:∵ OM平分∠AOB,ON平分∠BOD ,
∴ ∠BOM=∠BOA,∠BON=∠BOD,
∴ ∠MON=∠BOM+∠BON=(∠BOA+∠BOD)=∠AOD=80°.
(2)解: ①∵ OM 平分∠AOC,ON 平分∠BOD,
∴ ∠AOM=∠COM=∠AOC,∠DON=∠BON=∠BOD,
∵ ∠BOC=∠AOC+∠BOD-∠AOD=20°,
∴ ∠AOC+∠BOD=180°,
∴ ∠AOM+∠DON=(∠AOC+∠BOD)=90°,
∴ ∠MON=∠AOD-(∠AOM+∠DON)=160°-90°=70°;
②∵ ∠BOC在∠AOD内绕着点O以每秒的速度逆时针旋转t,∠BOC=20°,
∴ ∠AOC=∠AOB+∠BOC=10°+20°+t°=30°+t°,
∵ OM平分∠AOC,
∴ ∠AOM=∠AOC=15°+t°,
∵ ∠BOD=∠AOD-∠AOB=160°-(10°+t°)=150°-t,
∵ ON平分∠BOD,
∴ ∠DON=∠BOD=75°-t°,
∵ ∠AOM :∠DON=2:3 ,
∴ (15°+t°):(75°-t°)=2:3,
解得,t=42,
即t的值为42.
【分析】(1)根据角平分线的定义可得∠BOM=∠BOA,∠BON=∠BOD,即可求得;
(2) ① 根据角平分线的定义可得∠AOM=∠COM=∠AOC,∠DON=∠BON=∠BOD,根据∠BOC=∠AOC+∠BOD-∠AOD计算出∠AOC+∠BOD=180°,推出∠AOM+∠DON=90°,即可求得;
②根据角平分线的定义可得∠AOM=∠AOC=15°+t°,∠DON=∠BOD=75°-t°,再根据 ∠AOM:∠DON=2:3,列出方程,解方程即可求得.
23.(1),3
(2)或
(3)
21世纪教育网(www.21cnjy.com)
同课章节目录
