阶段质量评价(三) 成对数据的统计分析(含解析)高中数学人教A版(2019)选择性必修 第三册
文档属性
| 名称 | 阶段质量评价(三) 成对数据的统计分析(含解析)高中数学人教A版(2019)选择性必修 第三册 |  | |
| 格式 | docx | ||
| 文件大小 | 159.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 20:16:14 | ||
图片预览




文档简介
阶段质量评价(三) 成对数据的统计分析
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有一项是符合题目要求的)
1.已知经验回归方程=x+,其中=3,且样本点的中心为(1,2),则经验回归方程为 ( )
A.=x+3 B.=-2x+3
C.=-x+3 D.=x-3
2.根据一组样本数据(x1,y1),(x2,y2),…,(xn,yn)的散点图分析x与y之间是否存在线性相关关系,若求得其经验回归方程为=0.85x-85.7,则在样本点(165,57)处的残差为 ( )
A.54.55 B.2.45
C.3.45 D.111.55
3.如图所示的5个数据,去掉点D(3,10)后,下列说法错误的是 ( )
A.样本相关系数r变大
B.残差平方和变大
C.R2变大
D.解释变量x与响应变量y的相关性变强
4.为考察某种药物预防某疾病的效果,进行动物试验,得到如下列联表:
单位:只
患病 未患病 合计
服药 10 45 55
未服药 20 30 50
合计 30 75 105
则下列说法正确的是 ( )
附: χ2=,n=a+b+c+d.
α 0.05 0.01 0.001
xα 3.841 6.635 10.828
A.有95%的把握认为药物有效
B.有95%的把握认为药物无效
C.在犯错误的概率不超过0.05的前提下认为药物无效
D.在犯错误的概率不超过0.01的前提下认为药物有效
5.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽试验,由试验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是 ( )
A.y=a+bx B.y=a+bx2
C.y=a+bex D.y=a+bln x
6.某学校开展研究性学习活动,某同学获得一组试验数据如下:(1.99,1.5),(3,4.04),(4,7.5),(5.1,12),(6.12,18.01).对于这组数据,现在给出以下拟合曲线,其中拟合程度最好的是 ( )
A.y=2x-2 B.y=
C.y=log2x D.y=(x2-1)
7.为了研究某班学生的脚长x(单位:厘米)和身高y(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,设其经验回归方程为=x+.已知xi=225,yi=1 600,=4.该班某学生的脚长为24,据此估计其身高为 ( )
A.160 B.163
C.166 D.170
8.已知由成对样本数据(xi,yi),i=1,2,…,n求得的经验回归方程为=1.5x+0.5,且=3,现发现两个样本点(1.2,2.2)和(4.8,7.8)的残差较大,去除后重新求得的经验回归直线l的斜率为1.2,则去除后 ( )
A.新的经验回归方程为=1.2x+1.5
B.y的估计值的增加速度比原来变快
C.变量x与y具有正相关关系
D.样本点(2,3.75)的残差为0.05
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.下列说法正确的是 ( )
A.若变量x和y之间的样本相关系数为r=-0.992,则变量x和y之间的负相关性很强
B.用决定系数R2来比较两个模型拟合效果时,R2越大,残差平方和越小,模型的拟合效果越好
C.在经验回归方程=2-3.5x中,当解释变量每增加1个单位时,响应变量平均减少3.5个单位
D.经验回归直线=x+至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个
10.千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了地区A的100天日落和夜晚天气,得到如下2×2列联表(单位:天),并计算得到χ2≈19.05,下列小波对地区A天气的判断正确的是 ( )
日落云里走 夜晚天气
下雨 未下雨
出现 25 5
未出现 25 45
参考公式:χ2=
临界值参照表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
A.夜晚下雨的概率约为
B.未出现“日落云里走”,夜晚下雨的概率约为
C.根据小概率值α=0.01的独立性检验,认为“日落云里走”是否出现与夜晚天气有关
D.出现“日落云里走”, 根据小概率值α=0.01的独立性检验,可以认为夜晚会下雨
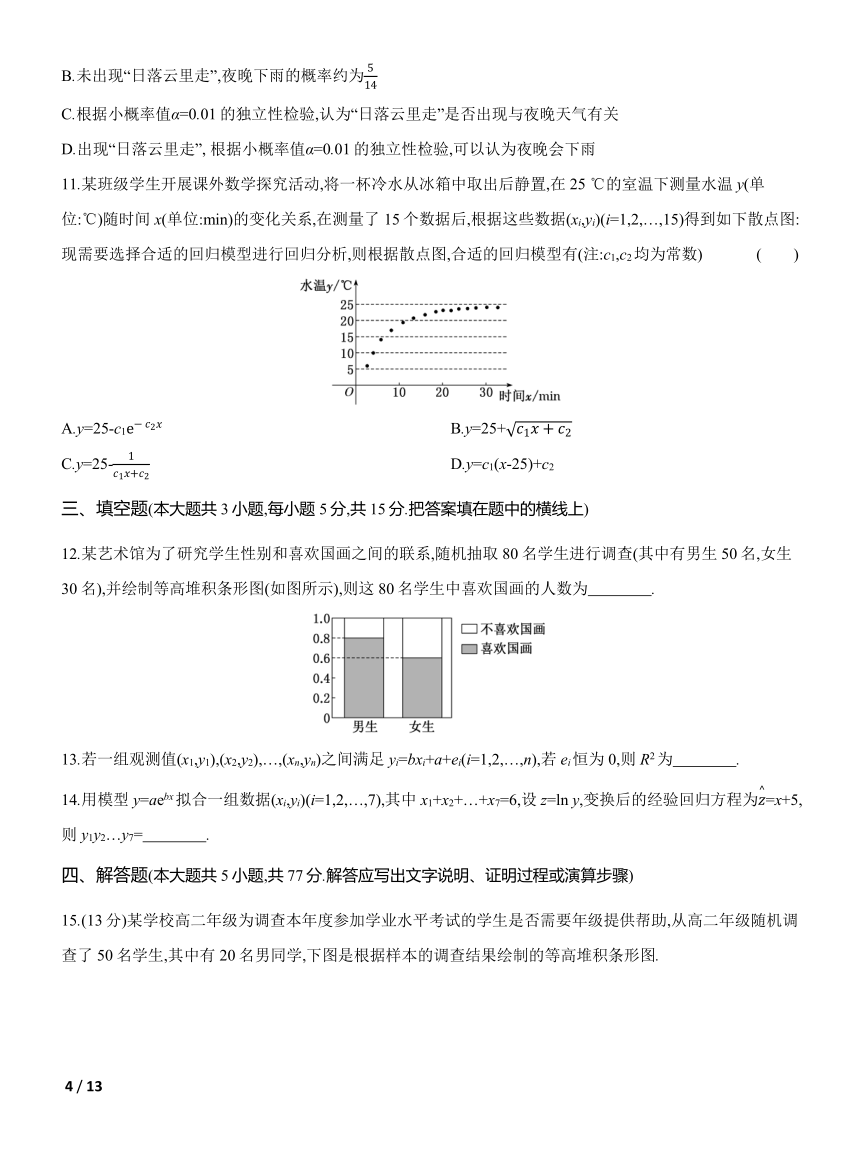
11.某班级学生开展课外数学探究活动,将一杯冷水从冰箱中取出后静置,在25 ℃的室温下测量水温y(单位:℃)随时间x(单位:min)的变化关系,在测量了15个数据后,根据这些数据(xi,yi)(i=1,2,…,15)得到如下散点图:
现需要选择合适的回归模型进行回归分析,则根据散点图,合适的回归模型有(注:c1,c2均为常数) ( )
A.y=25-c1 B.y=25+
C.y=25- D.y=c1(x-25)+c2
三、填空题(本大题共3小题,每小题5分,共15分.把答案填在题中的横线上)
12.某艺术馆为了研究学生性别和喜欢国画之间的联系,随机抽取80名学生进行调查(其中有男生50名,女生30名),并绘制等高堆积条形图(如图所示),则这80名学生中喜欢国画的人数为 .
13.若一组观测值(x1,y1),(x2,y2),…,(xn,yn)之间满足yi=bxi+a+ei(i=1,2,…,n),若ei恒为0,则R2为 .
14.用模型y=aebx拟合一组数据(xi,yi)(i=1,2,…,7),其中x1+x2+…+x7=6,设z=ln y,变换后的经验回归方程为=x+5,则y1y2…y7= .
四、解答题(本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)某学校高二年级为调查本年度参加学业水平考试的学生是否需要年级提供帮助,从高二年级随机调查了50名学生,其中有20名男同学,下图是根据样本的调查结果绘制的等高堆积条形图.
(1)根据已知条件与等高堆积条形图完成下面的2×2列联表:
单位:名
男同学 女同学 合计
需要帮助
不需要帮助
合计
(2)根据(1)中的2×2列联表及α=0.010的独立性检验,分析该校高二年级学生本年度参加学业水平考试需要年级提供帮助是否与性别有关.
附: χ2=,其中n=a+b+c+d.
α 0.050 0.010 0.001
xα 3.841 6.635 10.828
16.(15分)2024年某市开展了“寻找身边的好老师”活动,某中学积极行动,认真落实,通过微信关注评选“身边的好老师”,并对选出的五位“好老师”的班主任的工作年限和被关注数量进行了统计,得到如下数据:
班主任工作年限 x(单位:年) 4 6 8 10 12
被关注数量 y(单位:百人) 10 20 40 60 50
(1)若“好老师”的被关注数量y与其班主任的工作年限x满足经验回归方程,试求=x+,并就此分析:“好老师”的班主任工作年限为15年时被关注的数量;
(2)若用(i=1,2,3,4,5)表示统计数据时被关注数量的“即时均值”(四舍五入到整数),从“即时均值”中任选2组,求这2组数据之和小于8的概率.
17.(15分)某商场经营一批进价是30元/台的小商品,在市场调查中发现,此商品的销售单价x(x取整数)(元)与日销售量y(台)之间有如下关系:
x(元) 35 40 45 50
y(台) 56 41 28 11
(1)画出散点图,并判断y与x是否具有线性相关关系;
(2)求日销售量y对销售单价x的经验回归方程;
(3)设经营此商品的日销售利润为P元,根据(2)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.
18.(17分)某大型企业对其产品进行研发与创新,根据市场调研与模拟,得到研发投入x(亿元)与研发创新的直接收益y(亿元)的数据统计如下:
x 2 3 4 6 8 10 13 21 22 23 24 25
y 13 22 31 42 50 56 58 68.5 68 67.5 66 66
当017时,确定y与x满足的经验回归方程为=-0.7x+.
(1)根据下列表格中的数据,比较当0回归模型 模型① 模型②
回归方程 =4.1x+11.8 =21.3-14.4
(yi-i)2 182.4 79.2
(2)为鼓励科技创新,当研发的投入不少于20亿元时,国家给予公司补贴收益10亿元,以回归方程为预测依据,比较研发投入17亿元与20亿元时公司实际收益的大小;
(3)研发改造后,该公司F产品的效率X大幅提高,X服从正态分布N(0.52,0.012),公司对研发团队的奖励方案如下:若F产品的效率不超过50%,不予奖励;若F产品的效率超过50%但不超过53%,每件F产品奖励2万元;若F产品的效率超过53%,每件F产品奖励5万元.求每件F产品获得奖励的数学期望(保留两位小数).
附:①决定系数R2=1-;②==,=-;③若随机变量X服从正态分布N(μ,σ2),则P(μ-σ19.(17分)某班级共有50名同学(男女各占一半),为弘扬传统文化,班委组织了“古诗词男女对抗赛”,将同学随机分成25组,每组男、女同学各一名,每名同学均回答同样的五个不同问题,答对一题得一分,答错或不答得零分,满分为5分.最后25组同学得分如表:
组别号 1 2 3 4 5 6 7 8 9 10 11 12 13
男同学 得分 5 4 5 5 4 5 5 4 4 4 5 5 4
女同学 得分 4 3 4 5 5 5 4 5 5 5 5 3 5
分差 1 1 1 0 -1 0 1 -1 -1 -1 0 2 -1
组别号 14 15 16 17 18 19 20 21 22 23 24 25
男同学 得分 4 3 4 4 4 4 5 5 5 4 3 3
女同学 得分 5 3 4 5 4 3 5 5 3 4 5 5
分差 -1 0 0 -1 0 1 0 0 2 0 -2 -2
(1)完成2×2列联表,并依据α=0.1的独立性检验,分析该次对抗赛是否得满分与性别是否有关;
(2)某课题研究小组假设各组男、女同学分差服从正态分布N(μ,σ2),首先根据前20组男、女同学的分差确定μ和σ,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男、女同学分差与μ的差的绝对值分别为xi(i=1,2,3,4,5),若出现下列两种情况之一,则不接受该模型,否则接受该模型.
①存在xi≥3σ;
②记满足2σ该课题研究小组是否会接受该模型
参考公式和数据:χ2=,≈0.894,≈0.949,0.9575≈0.803,43×0.9574≈36,432×0.9573≈1 621;若X~N(μ,σ2),则P(μ-2σα 0.1 0.05 0.01
xα 2.706 3.841 6.635
阶段质量评价(三)
1.选C 因为经验回归直线一定经过样本点的中心,所以2=+3,解得=-1,所以经验回归方程为=-x+3.
2.选B 把x=165代入=0.85x-85.7,得=0.85×165-85.7=54.55,所以在样本点(165,57)处的残差为57-54.55=2.45.故选B.
3.选B 由题中散点图知去掉点D后,x与y的相关性变强,且为正相关,所以r变大,R2变大,残差平方和变小.
4.选A 根据题中列联表,计算得χ2==≈6.109,由6.109>3.841=x0.05且6.109<6.635=x0.01可知,有95%的把握认为药物有效.故选A.
5.选D 观察散点图可知,散点用光滑曲线连接起来后比较接近对数型函数的图象,故选D.
6.选D 直线y=2x-2是均匀变化的,不符合要求;指数函数y=是单调递减的,不符合要求;对数函数y=log2x的增长缓慢,不符合要求;将各组数据代入选项D中,基本符合要求.
7.选C 由题意可知=22.5,=160,∴160=4×22.5+,解得=70,∴=4x+70,∴当x=24时,=4×24+70=166.故选C.
8.选C ∵=3,去除前的经验回归方程为=1.5x+0.5,∴=5.设重新求得的经验回归直线l的方程为=+x,则=1.2,∴变量x与y具有正相关关系,故C正确.设新的成对样本数据为(x'i,y'i),i=1,2,…,n-2,x'i的平均值为',y'i的平均值为',则(n-2)'=n-(1.2+4.8)=3n-6=3(n-2),(n-2)'=n-(2.2+7.8)=5n-10=5(n-2),故'=3,'=5,∴='-'=5-1.2×3=1.4.故新的经验回归方程为=1.2x+1.4,故A错误.∵1.2<1.5,∴去除后y的估计值的增加速度比原来变慢,故B错误.把x=2代入新的经验回归方程中,得=3.8,∴样本点(2,3.75)的残差为3.75-3.8=-0.05,故D错误.故选C.
9.ABC
10.选ABC 由列联表知,100天中有50天下雨,50天未下雨,因此夜晚下雨的概率约为=,A正确;未出现“日落云里走”,夜晚下雨的概率约为=,B正确;χ2=≈19.05>6.635,因此根据小概率值α=0.01的独立性检验,认为“日落云里走”是否出现与夜晚天气有关,C正确,D错误.故选ABC.
11.选AC 题中散点图的特点是y随x的增加而增加,增加的速度越来越慢,且y<25.对于A,当c1>0,c2>0时符合题意;对于B,y=25+≥25,不符合题意;对于C,当c1>0,c2>0时符合题意;对于D,y=c1(x-25)+c2的增长速度保持不变,不符合题意.故选AC.
12.解析:由等高堆积条形图可知,男生中喜欢国画的占80%,女生中喜欢国画的占60%,则这80名学生中喜欢国画的人数为50×80%+30×60%=58.
答案:58
13.解析:ei恒为0,说明随机误差对yi贡献为0,这时候变量x,y之间是函数关系,故R2=1.
答案:1
14.解析:因为x1+x2+…+x7=6,所以==,所以=+5=+5=,即===,所以ln(y1y2…y7)=41,即y1y2…y7=e41.
答案:e41
15.解:(1)由题意知调查的50名学生中有20名男同学,30名女同学.
由题中等高堆积条形图可知,男同学中需要帮助的有4人,不需要帮助的有16人,女同学中需要帮助的有3人,不需要帮助的有27人.
则2×2列联表为
单位:名
男同学 女同学 合计
需要帮助 4 3 7
不需要帮助 16 27 43
合计 20 30 50
(2)零假设H0:该校高二年级学生本年度参加学业水平考试需要年级提供帮助与性别无关.经计算得χ2=≈0.997<6.635=x0.010,
依据α=0.010的独立性检验,没有充分证据推断H0不成立,因此认为H0成立,即认为该校高二年级学生本年度参加学业水平考试需要年级提供帮助与性别无关.
16.解:(1)由题意得=8,=36,
==6,
=36-48=-12,所以=6x-12,
当x=15时,=6×15-12=78(百人)=7 800(人).
(2)这5组统计数据,被关注数量的“即时均值”分别为3,3,5,6,4.
从5组“即时均值”任选2组,共有=10种情况,其中2组数据之和小于8为(3,3),(3,4),(3,4)共3种情况,所以这2组数据之和小于8的概率为.
17.解:(1)散点图如图所示,从图中可以看出这些点大致分布在一条直线附近,因此两个变量线性相关.
(2) 因为=×(35+40+45+50)=42.5,
=×(56+41+28+11)=34,
xiyi=35×56+40×41+45×28+50×11=5 410,
x=352+402+452+502=7 350,
所以===≈-3.
=-=34-(-3)×42.5=161.5.
所以经验回归方程为=161.5-3x.
(3)依题意,有P=(161.5-3x)(x-30)=-3x2+251.5x-4 845=-3+-4 845.
所以当x=≈42时,P有最大值,约为426元.即预测当销售单价为42元时,能获得最大日销售利润.
18.解: (1)由题表得182.4>79.2,即>,所以模型①的决定系数小于模型②的决定系数,说明回归模型②的拟合精度更高、更可靠.
当x=17时,=21.3×-14.4≈21.3×4.1-14.4=72.93.
所以预测该企业对产品研发的投入为17亿元时的直接收益为72.93亿元.
(2)当x>17时,由已知可得
-20==3,
-60==7.2,
所以=23,=67.2,
所以=+0.7=67.2+0.7×23=83.3,
所以当x>17时,y与x满足的经验回归方程为=-0.7x+83.3.
当x=20时,=-0.7×20+83.3=69.3.
所以当x=20时,实际收益的预测值为69.3+10=79.3(亿元),因为79.3>72.93,
所以研发投入20亿元时公司的实际收益更大.
(3)因为P(0.52-0.02所以P(X>0.50)≈0.5+=0.977 2,P(X≤0.50)=1-P(X>0.50)=0.022 8,
因为P(0.52-0.01所以P(X>0.53)≈0.5-=0.158 7,
所以P(0.50设每件F产品获得的奖励为Y万元,则Y的分布列为
Y 0 2 5
P 0.022 8 0.818 5 0.158 7
所以E(Y)=0×0.022 8+2×0.818 5+5×0.158 7≈2.43(万元).
19.解:(1)2×2列联表如下:
单位:名
男同学 女同学 合计
对抗赛得满分 10 14 24
对抗赛未得满分 15 11 26
合计 25 25 50
零假设H0:该次对抗赛是否得满分与性别无关,经计算得χ2=≈1.282<2.706=x0.1,依据α=0.1的独立性检验,没有充分证据推断H0不成立,因此认为H0成立,即认为该次对抗赛是否得满分与性别无关.
(2)由题意知μ=0,σ2=0.8.
所以x1=0,x2=2,x3=0,x4=2,x5=2.
因为2σ=2×≈2×0.894=1.788,3σ=3×≈3×0.894=2.682,
所以不存在xi≥3σ.
因为满足2σ当X~N(μ,σ2)时,P(μ-3σ设从服从正态分布N(μ,σ2)的总体中任意取5个个体,其中值在区间(μ-3σ,μ-2σ)∪(μ+2σ,μ+3σ)内的个体数为Y,则Y~B(5,0.043),
所以P(Y≥3)=1-0.9575-×0.043×0.9574-×0.0432×0.9573≈1-0.803-5×0.001×36-10×10-6×1 621=0.000 79<0.003.
综上,第②种情况出现,所以该课题研究小组不会接受该模型.
2 / 7
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有一项是符合题目要求的)
1.已知经验回归方程=x+,其中=3,且样本点的中心为(1,2),则经验回归方程为 ( )
A.=x+3 B.=-2x+3
C.=-x+3 D.=x-3
2.根据一组样本数据(x1,y1),(x2,y2),…,(xn,yn)的散点图分析x与y之间是否存在线性相关关系,若求得其经验回归方程为=0.85x-85.7,则在样本点(165,57)处的残差为 ( )
A.54.55 B.2.45
C.3.45 D.111.55
3.如图所示的5个数据,去掉点D(3,10)后,下列说法错误的是 ( )
A.样本相关系数r变大
B.残差平方和变大
C.R2变大
D.解释变量x与响应变量y的相关性变强
4.为考察某种药物预防某疾病的效果,进行动物试验,得到如下列联表:
单位:只
患病 未患病 合计
服药 10 45 55
未服药 20 30 50
合计 30 75 105
则下列说法正确的是 ( )
附: χ2=,n=a+b+c+d.
α 0.05 0.01 0.001
xα 3.841 6.635 10.828
A.有95%的把握认为药物有效
B.有95%的把握认为药物无效
C.在犯错误的概率不超过0.05的前提下认为药物无效
D.在犯错误的概率不超过0.01的前提下认为药物有效
5.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽试验,由试验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是 ( )
A.y=a+bx B.y=a+bx2
C.y=a+bex D.y=a+bln x
6.某学校开展研究性学习活动,某同学获得一组试验数据如下:(1.99,1.5),(3,4.04),(4,7.5),(5.1,12),(6.12,18.01).对于这组数据,现在给出以下拟合曲线,其中拟合程度最好的是 ( )
A.y=2x-2 B.y=
C.y=log2x D.y=(x2-1)
7.为了研究某班学生的脚长x(单位:厘米)和身高y(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,设其经验回归方程为=x+.已知xi=225,yi=1 600,=4.该班某学生的脚长为24,据此估计其身高为 ( )
A.160 B.163
C.166 D.170
8.已知由成对样本数据(xi,yi),i=1,2,…,n求得的经验回归方程为=1.5x+0.5,且=3,现发现两个样本点(1.2,2.2)和(4.8,7.8)的残差较大,去除后重新求得的经验回归直线l的斜率为1.2,则去除后 ( )
A.新的经验回归方程为=1.2x+1.5
B.y的估计值的增加速度比原来变快
C.变量x与y具有正相关关系
D.样本点(2,3.75)的残差为0.05
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.下列说法正确的是 ( )
A.若变量x和y之间的样本相关系数为r=-0.992,则变量x和y之间的负相关性很强
B.用决定系数R2来比较两个模型拟合效果时,R2越大,残差平方和越小,模型的拟合效果越好
C.在经验回归方程=2-3.5x中,当解释变量每增加1个单位时,响应变量平均减少3.5个单位
D.经验回归直线=x+至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个
10.千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了地区A的100天日落和夜晚天气,得到如下2×2列联表(单位:天),并计算得到χ2≈19.05,下列小波对地区A天气的判断正确的是 ( )
日落云里走 夜晚天气
下雨 未下雨
出现 25 5
未出现 25 45
参考公式:χ2=
临界值参照表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
A.夜晚下雨的概率约为
B.未出现“日落云里走”,夜晚下雨的概率约为
C.根据小概率值α=0.01的独立性检验,认为“日落云里走”是否出现与夜晚天气有关
D.出现“日落云里走”, 根据小概率值α=0.01的独立性检验,可以认为夜晚会下雨
11.某班级学生开展课外数学探究活动,将一杯冷水从冰箱中取出后静置,在25 ℃的室温下测量水温y(单位:℃)随时间x(单位:min)的变化关系,在测量了15个数据后,根据这些数据(xi,yi)(i=1,2,…,15)得到如下散点图:
现需要选择合适的回归模型进行回归分析,则根据散点图,合适的回归模型有(注:c1,c2均为常数) ( )
A.y=25-c1 B.y=25+
C.y=25- D.y=c1(x-25)+c2
三、填空题(本大题共3小题,每小题5分,共15分.把答案填在题中的横线上)
12.某艺术馆为了研究学生性别和喜欢国画之间的联系,随机抽取80名学生进行调查(其中有男生50名,女生30名),并绘制等高堆积条形图(如图所示),则这80名学生中喜欢国画的人数为 .
13.若一组观测值(x1,y1),(x2,y2),…,(xn,yn)之间满足yi=bxi+a+ei(i=1,2,…,n),若ei恒为0,则R2为 .
14.用模型y=aebx拟合一组数据(xi,yi)(i=1,2,…,7),其中x1+x2+…+x7=6,设z=ln y,变换后的经验回归方程为=x+5,则y1y2…y7= .
四、解答题(本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)某学校高二年级为调查本年度参加学业水平考试的学生是否需要年级提供帮助,从高二年级随机调查了50名学生,其中有20名男同学,下图是根据样本的调查结果绘制的等高堆积条形图.
(1)根据已知条件与等高堆积条形图完成下面的2×2列联表:
单位:名
男同学 女同学 合计
需要帮助
不需要帮助
合计
(2)根据(1)中的2×2列联表及α=0.010的独立性检验,分析该校高二年级学生本年度参加学业水平考试需要年级提供帮助是否与性别有关.
附: χ2=,其中n=a+b+c+d.
α 0.050 0.010 0.001
xα 3.841 6.635 10.828
16.(15分)2024年某市开展了“寻找身边的好老师”活动,某中学积极行动,认真落实,通过微信关注评选“身边的好老师”,并对选出的五位“好老师”的班主任的工作年限和被关注数量进行了统计,得到如下数据:
班主任工作年限 x(单位:年) 4 6 8 10 12
被关注数量 y(单位:百人) 10 20 40 60 50
(1)若“好老师”的被关注数量y与其班主任的工作年限x满足经验回归方程,试求=x+,并就此分析:“好老师”的班主任工作年限为15年时被关注的数量;
(2)若用(i=1,2,3,4,5)表示统计数据时被关注数量的“即时均值”(四舍五入到整数),从“即时均值”中任选2组,求这2组数据之和小于8的概率.
17.(15分)某商场经营一批进价是30元/台的小商品,在市场调查中发现,此商品的销售单价x(x取整数)(元)与日销售量y(台)之间有如下关系:
x(元) 35 40 45 50
y(台) 56 41 28 11
(1)画出散点图,并判断y与x是否具有线性相关关系;
(2)求日销售量y对销售单价x的经验回归方程;
(3)设经营此商品的日销售利润为P元,根据(2)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.
18.(17分)某大型企业对其产品进行研发与创新,根据市场调研与模拟,得到研发投入x(亿元)与研发创新的直接收益y(亿元)的数据统计如下:
x 2 3 4 6 8 10 13 21 22 23 24 25
y 13 22 31 42 50 56 58 68.5 68 67.5 66 66
当0
(1)根据下列表格中的数据,比较当0
回归方程 =4.1x+11.8 =21.3-14.4
(yi-i)2 182.4 79.2
(2)为鼓励科技创新,当研发的投入不少于20亿元时,国家给予公司补贴收益10亿元,以回归方程为预测依据,比较研发投入17亿元与20亿元时公司实际收益的大小;
(3)研发改造后,该公司F产品的效率X大幅提高,X服从正态分布N(0.52,0.012),公司对研发团队的奖励方案如下:若F产品的效率不超过50%,不予奖励;若F产品的效率超过50%但不超过53%,每件F产品奖励2万元;若F产品的效率超过53%,每件F产品奖励5万元.求每件F产品获得奖励的数学期望(保留两位小数).
附:①决定系数R2=1-;②==,=-;③若随机变量X服从正态分布N(μ,σ2),则P(μ-σ
组别号 1 2 3 4 5 6 7 8 9 10 11 12 13
男同学 得分 5 4 5 5 4 5 5 4 4 4 5 5 4
女同学 得分 4 3 4 5 5 5 4 5 5 5 5 3 5
分差 1 1 1 0 -1 0 1 -1 -1 -1 0 2 -1
组别号 14 15 16 17 18 19 20 21 22 23 24 25
男同学 得分 4 3 4 4 4 4 5 5 5 4 3 3
女同学 得分 5 3 4 5 4 3 5 5 3 4 5 5
分差 -1 0 0 -1 0 1 0 0 2 0 -2 -2
(1)完成2×2列联表,并依据α=0.1的独立性检验,分析该次对抗赛是否得满分与性别是否有关;
(2)某课题研究小组假设各组男、女同学分差服从正态分布N(μ,σ2),首先根据前20组男、女同学的分差确定μ和σ,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男、女同学分差与μ的差的绝对值分别为xi(i=1,2,3,4,5),若出现下列两种情况之一,则不接受该模型,否则接受该模型.
①存在xi≥3σ;
②记满足2σ
参考公式和数据:χ2=,≈0.894,≈0.949,0.9575≈0.803,43×0.9574≈36,432×0.9573≈1 621;若X~N(μ,σ2),则P(μ-2σ
xα 2.706 3.841 6.635
阶段质量评价(三)
1.选C 因为经验回归直线一定经过样本点的中心,所以2=+3,解得=-1,所以经验回归方程为=-x+3.
2.选B 把x=165代入=0.85x-85.7,得=0.85×165-85.7=54.55,所以在样本点(165,57)处的残差为57-54.55=2.45.故选B.
3.选B 由题中散点图知去掉点D后,x与y的相关性变强,且为正相关,所以r变大,R2变大,残差平方和变小.
4.选A 根据题中列联表,计算得χ2==≈6.109,由6.109>3.841=x0.05且6.109<6.635=x0.01可知,有95%的把握认为药物有效.故选A.
5.选D 观察散点图可知,散点用光滑曲线连接起来后比较接近对数型函数的图象,故选D.
6.选D 直线y=2x-2是均匀变化的,不符合要求;指数函数y=是单调递减的,不符合要求;对数函数y=log2x的增长缓慢,不符合要求;将各组数据代入选项D中,基本符合要求.
7.选C 由题意可知=22.5,=160,∴160=4×22.5+,解得=70,∴=4x+70,∴当x=24时,=4×24+70=166.故选C.
8.选C ∵=3,去除前的经验回归方程为=1.5x+0.5,∴=5.设重新求得的经验回归直线l的方程为=+x,则=1.2,∴变量x与y具有正相关关系,故C正确.设新的成对样本数据为(x'i,y'i),i=1,2,…,n-2,x'i的平均值为',y'i的平均值为',则(n-2)'=n-(1.2+4.8)=3n-6=3(n-2),(n-2)'=n-(2.2+7.8)=5n-10=5(n-2),故'=3,'=5,∴='-'=5-1.2×3=1.4.故新的经验回归方程为=1.2x+1.4,故A错误.∵1.2<1.5,∴去除后y的估计值的增加速度比原来变慢,故B错误.把x=2代入新的经验回归方程中,得=3.8,∴样本点(2,3.75)的残差为3.75-3.8=-0.05,故D错误.故选C.
9.ABC
10.选ABC 由列联表知,100天中有50天下雨,50天未下雨,因此夜晚下雨的概率约为=,A正确;未出现“日落云里走”,夜晚下雨的概率约为=,B正确;χ2=≈19.05>6.635,因此根据小概率值α=0.01的独立性检验,认为“日落云里走”是否出现与夜晚天气有关,C正确,D错误.故选ABC.
11.选AC 题中散点图的特点是y随x的增加而增加,增加的速度越来越慢,且y<25.对于A,当c1>0,c2>0时符合题意;对于B,y=25+≥25,不符合题意;对于C,当c1>0,c2>0时符合题意;对于D,y=c1(x-25)+c2的增长速度保持不变,不符合题意.故选AC.
12.解析:由等高堆积条形图可知,男生中喜欢国画的占80%,女生中喜欢国画的占60%,则这80名学生中喜欢国画的人数为50×80%+30×60%=58.
答案:58
13.解析:ei恒为0,说明随机误差对yi贡献为0,这时候变量x,y之间是函数关系,故R2=1.
答案:1
14.解析:因为x1+x2+…+x7=6,所以==,所以=+5=+5=,即===,所以ln(y1y2…y7)=41,即y1y2…y7=e41.
答案:e41
15.解:(1)由题意知调查的50名学生中有20名男同学,30名女同学.
由题中等高堆积条形图可知,男同学中需要帮助的有4人,不需要帮助的有16人,女同学中需要帮助的有3人,不需要帮助的有27人.
则2×2列联表为
单位:名
男同学 女同学 合计
需要帮助 4 3 7
不需要帮助 16 27 43
合计 20 30 50
(2)零假设H0:该校高二年级学生本年度参加学业水平考试需要年级提供帮助与性别无关.经计算得χ2=≈0.997<6.635=x0.010,
依据α=0.010的独立性检验,没有充分证据推断H0不成立,因此认为H0成立,即认为该校高二年级学生本年度参加学业水平考试需要年级提供帮助与性别无关.
16.解:(1)由题意得=8,=36,
==6,
=36-48=-12,所以=6x-12,
当x=15时,=6×15-12=78(百人)=7 800(人).
(2)这5组统计数据,被关注数量的“即时均值”分别为3,3,5,6,4.
从5组“即时均值”任选2组,共有=10种情况,其中2组数据之和小于8为(3,3),(3,4),(3,4)共3种情况,所以这2组数据之和小于8的概率为.
17.解:(1)散点图如图所示,从图中可以看出这些点大致分布在一条直线附近,因此两个变量线性相关.
(2) 因为=×(35+40+45+50)=42.5,
=×(56+41+28+11)=34,
xiyi=35×56+40×41+45×28+50×11=5 410,
x=352+402+452+502=7 350,
所以===≈-3.
=-=34-(-3)×42.5=161.5.
所以经验回归方程为=161.5-3x.
(3)依题意,有P=(161.5-3x)(x-30)=-3x2+251.5x-4 845=-3+-4 845.
所以当x=≈42时,P有最大值,约为426元.即预测当销售单价为42元时,能获得最大日销售利润.
18.解: (1)由题表得182.4>79.2,即>,所以模型①的决定系数小于模型②的决定系数,说明回归模型②的拟合精度更高、更可靠.
当x=17时,=21.3×-14.4≈21.3×4.1-14.4=72.93.
所以预测该企业对产品研发的投入为17亿元时的直接收益为72.93亿元.
(2)当x>17时,由已知可得
-20==3,
-60==7.2,
所以=23,=67.2,
所以=+0.7=67.2+0.7×23=83.3,
所以当x>17时,y与x满足的经验回归方程为=-0.7x+83.3.
当x=20时,=-0.7×20+83.3=69.3.
所以当x=20时,实际收益的预测值为69.3+10=79.3(亿元),因为79.3>72.93,
所以研发投入20亿元时公司的实际收益更大.
(3)因为P(0.52-0.02
因为P(0.52-0.01
所以P(0.50
Y 0 2 5
P 0.022 8 0.818 5 0.158 7
所以E(Y)=0×0.022 8+2×0.818 5+5×0.158 7≈2.43(万元).
19.解:(1)2×2列联表如下:
单位:名
男同学 女同学 合计
对抗赛得满分 10 14 24
对抗赛未得满分 15 11 26
合计 25 25 50
零假设H0:该次对抗赛是否得满分与性别无关,经计算得χ2=≈1.282<2.706=x0.1,依据α=0.1的独立性检验,没有充分证据推断H0不成立,因此认为H0成立,即认为该次对抗赛是否得满分与性别无关.
(2)由题意知μ=0,σ2=0.8.
所以x1=0,x2=2,x3=0,x4=2,x5=2.
因为2σ=2×≈2×0.894=1.788,3σ=3×≈3×0.894=2.682,
所以不存在xi≥3σ.
因为满足2σ
所以P(Y≥3)=1-0.9575-×0.043×0.9574-×0.0432×0.9573≈1-0.803-5×0.001×36-10×10-6×1 621=0.000 79<0.003.
综上,第②种情况出现,所以该课题研究小组不会接受该模型.
2 / 7
