人教B版高中数学选择性必修第一册1.1.2空间向量基本定理教学 课件(共24张PPT)
文档属性
| 名称 | 人教B版高中数学选择性必修第一册1.1.2空间向量基本定理教学 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
1.1.2 空间向量基本定理
主讲:
人教B版选择性必修第一册
第1章 空间向量
1.共线向量基本定理的内容是什么?
复习回顾
如果a≠0且b//a,则存在唯一的实数λ,使得b=λa.
2.平面向量基本定理的内容是什么?
如果平面内两个向量a与b不共线,则对该平面内任意一个向量c,存在唯一的实数对(x,y),使得c=xa+yb
上述结论在空间中仍成立吗?如何判断空间中的三个向量是否共面?
尝试与发现
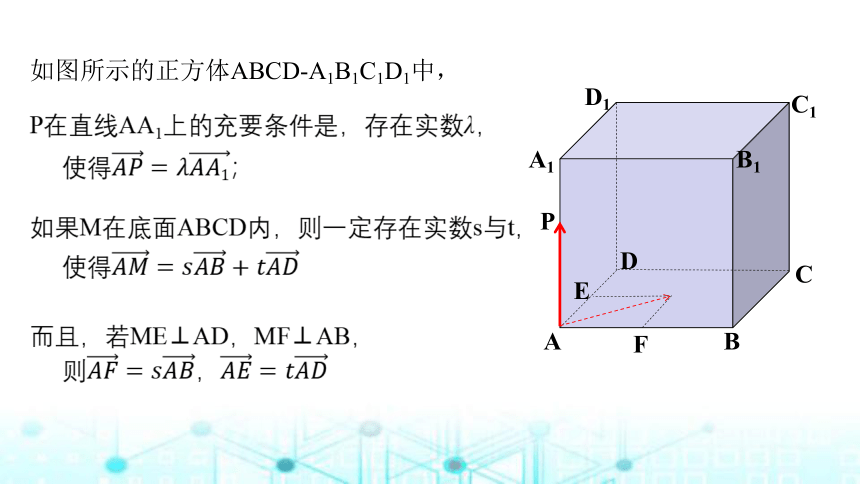
如图所示的正方体ABCD-A1B1C1D1中,
A
B
C
D
A1
B1
C1
D1
E
F
P
一、共面向量定理
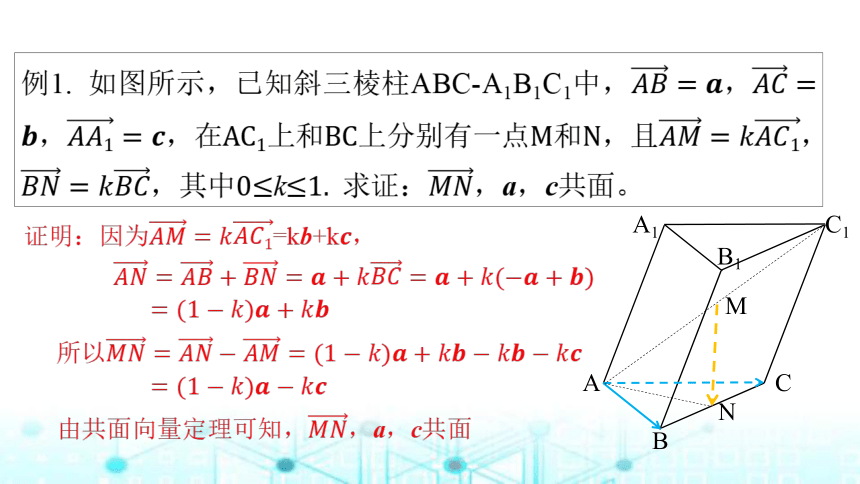
【典型例题一】共面向量定理的应用
A
B
C
N
M
A1
B1
C1
【典型例题一】共面向量定理的应用
若A,B,C三点不共线,则点P在平面ABC内需要满足什么条件?
尝试与发现
回忆平面向量基本定理的内容,两个不共线的向量可以表示平面中任何一个向量。那么任意一个空间向量可以用什么样的向量来表示呢?
尝试与发现
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
a
b
c
p
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
a
b
c
O
P
α
p
a
c
b
B
C
A
Q
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
a
b
c
O
P
α
p
a
c
b
B
C
A
Q
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
O
Q
P
p
a
c
b
B
C
A
α
a
b
c
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
xa
O
Q
P
p
a
c
b
yb
zc
B
C
A
α
a
b
c
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
xa
O
Q
P
p
a
c
b
yb
zc
B
C
A
α
a
b
c
二、空间向量基本定理
如果空间中的三个向量 a,b,c 不共面,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),使得
p=xa+yb+zc.
表达式xa+yb+zc一般称为向量a,b,c的线性组合或线性表达式。
把空间中不共面的三个向量a,b,c组成空间向量的一组基底,a,b,c 都叫做基向量.
【典型例题二】空间向量基本定理的应用
A
B
C
D
A1
B1
C1
D1
【典型例题二】空间向量基本定理的应用
A
B
C
A1
B1
C1
D
【典型例题二】空间向量基本定理的应用
【典型例题二】空间向量基本定理的应用
C
当堂练习
C
当堂练习
C
当堂练习
课堂小结
1.1.2 空间向量基本定理
主讲:
人教B版选择性必修第一册
第1章 空间向量
1.共线向量基本定理的内容是什么?
复习回顾
如果a≠0且b//a,则存在唯一的实数λ,使得b=λa.
2.平面向量基本定理的内容是什么?
如果平面内两个向量a与b不共线,则对该平面内任意一个向量c,存在唯一的实数对(x,y),使得c=xa+yb
上述结论在空间中仍成立吗?如何判断空间中的三个向量是否共面?
尝试与发现
如图所示的正方体ABCD-A1B1C1D1中,
A
B
C
D
A1
B1
C1
D1
E
F
P
一、共面向量定理
【典型例题一】共面向量定理的应用
A
B
C
N
M
A1
B1
C1
【典型例题一】共面向量定理的应用
若A,B,C三点不共线,则点P在平面ABC内需要满足什么条件?
尝试与发现
回忆平面向量基本定理的内容,两个不共线的向量可以表示平面中任何一个向量。那么任意一个空间向量可以用什么样的向量来表示呢?
尝试与发现
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
a
b
c
p
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
a
b
c
O
P
α
p
a
c
b
B
C
A
Q
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
a
b
c
O
P
α
p
a
c
b
B
C
A
Q
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
O
Q
P
p
a
c
b
B
C
A
α
a
b
c
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
xa
O
Q
P
p
a
c
b
yb
zc
B
C
A
α
a
b
c
在空间中,如果用任意三个不共面的向量a,b,c表示空间任意向量p,你能得出什么结论?
xa
O
Q
P
p
a
c
b
yb
zc
B
C
A
α
a
b
c
二、空间向量基本定理
如果空间中的三个向量 a,b,c 不共面,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),使得
p=xa+yb+zc.
表达式xa+yb+zc一般称为向量a,b,c的线性组合或线性表达式。
把空间中不共面的三个向量a,b,c组成空间向量的一组基底,a,b,c 都叫做基向量.
【典型例题二】空间向量基本定理的应用
A
B
C
D
A1
B1
C1
D1
【典型例题二】空间向量基本定理的应用
A
B
C
A1
B1
C1
D
【典型例题二】空间向量基本定理的应用
【典型例题二】空间向量基本定理的应用
C
当堂练习
C
当堂练习
C
当堂练习
课堂小结
