人教B版高中数学选择性必修第一册1.2.5空间中的距离 课件(共16张PPT)
文档属性
| 名称 | 人教B版高中数学选择性必修第一册1.2.5空间中的距离 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
1.2.4 二面角
主讲:张明明
人教B版选择性必修第一册
第1章 空间向量
“距离”在生活中随处可见,例如,我们常说某两地之间的距离是多少,汽车的刹车距离是多少,等等。数学中的“距离”概念是从生活中的具体问题中抽象出来的,要求具有准确的定义,以避免歧义,到目前为止,你学过哪些平面内的“距离”?这些“距离”的定义有什么共同点?由此你能得到空间中任意两个图形之间的距离具有的性质吗?
空间中两点之间的距离指的仍是这两个点连线的线段长。
一、空间中两点之间的距离
A
B
因为向量的长度表示的是向量的始点与终点之间的距离,所以可以通过向量来求空间中两点之间的距离。
|=
设A(x1,y1,z1),B(x2,y2,z2)为空间中任意两点,则
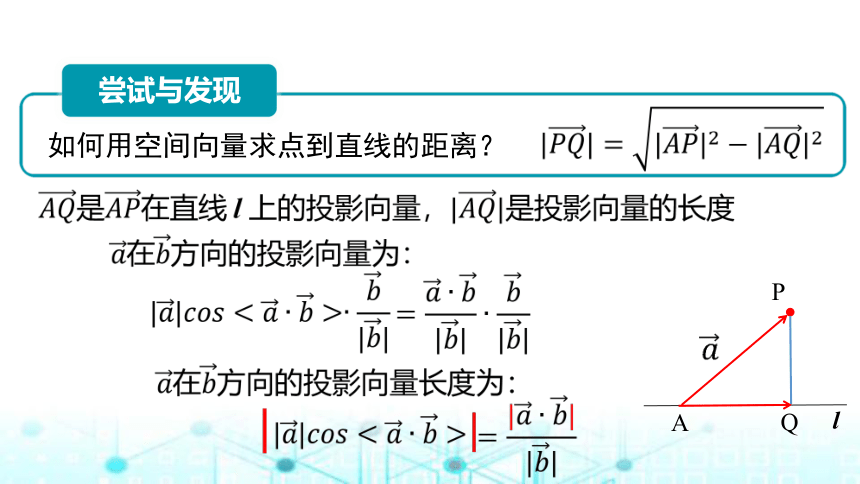
如何用空间向量求点到直线的距离?
A
Q
P
l
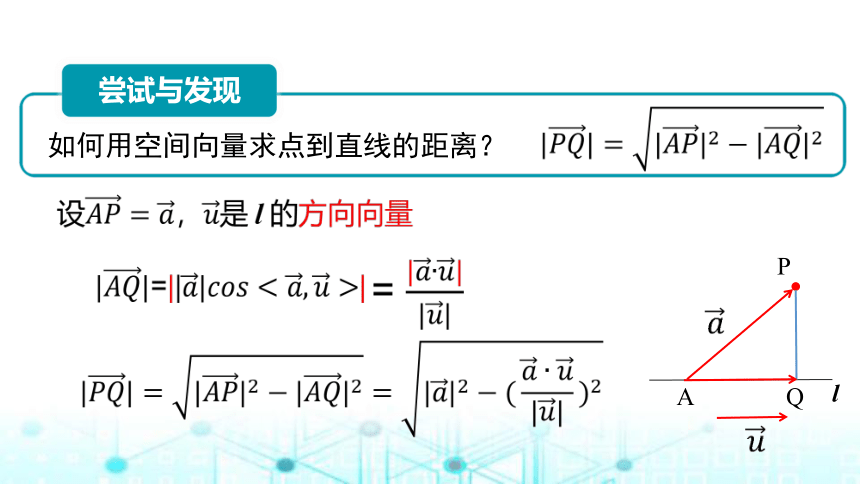
如何用空间向量求点到直线的距离?
A
Q
P
l
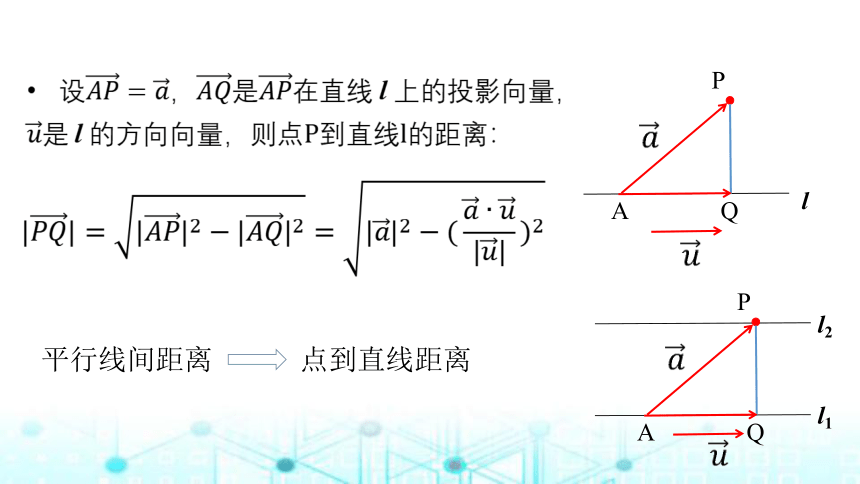
二、点到之间的距离
A
Q
P
l
思考:两条平行线间的距离应该如何表示?
l1
l2
A
Q
P
二、点到之间的距离
A
Q
P
l
l1
l2
A
Q
P
平行线间距离
点到直线距离
【典型例题一】
例1 已知直线 l 经过点A(2,3,1),若向量u=(1,0,-1)是直线 l 的方向向量,则点P(4,3,2)到 l 的距离为_____
A
P
l
Q
【典型例题一】
变式 已知直线 l 经过点A(2,3,1),若向量n=(1,0,-1)所在直线与 l 垂直,则点P(4,3,2)到 l 的距离为_____
A
P
l
Q
n
如何用空间向量求点到平面的距离?
A
Q
P
l
α
三、点到平面的距离
A
Q
P
α
P
l
α
β
思考:直线和平面平行,则线面距离如何求解?
两个平行平面的距离呢?
三、点到平面的距离
A
Q
P
α
P
l
α
β
平行的线面距离
点到平面距离
平行的平面距离
【典型例题二】
例2 已知平面α的一个法向量n=(-2,-2,1),点A(-1,3,0)在α内,则P(-2,1,4)到α的距离为( )
答案: D
【典型例题二】
练习 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离。
A1
B1
C1
D1
A
D
C
B
E
F
x
z
y
【典型例题二】
练习 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离。
A1
B1
C1
D1
A
D
C
B
E
F
x
z
y
课堂小结
1.2.4 二面角
主讲:张明明
人教B版选择性必修第一册
第1章 空间向量
“距离”在生活中随处可见,例如,我们常说某两地之间的距离是多少,汽车的刹车距离是多少,等等。数学中的“距离”概念是从生活中的具体问题中抽象出来的,要求具有准确的定义,以避免歧义,到目前为止,你学过哪些平面内的“距离”?这些“距离”的定义有什么共同点?由此你能得到空间中任意两个图形之间的距离具有的性质吗?
空间中两点之间的距离指的仍是这两个点连线的线段长。
一、空间中两点之间的距离
A
B
因为向量的长度表示的是向量的始点与终点之间的距离,所以可以通过向量来求空间中两点之间的距离。
|=
设A(x1,y1,z1),B(x2,y2,z2)为空间中任意两点,则
如何用空间向量求点到直线的距离?
A
Q
P
l
如何用空间向量求点到直线的距离?
A
Q
P
l
二、点到之间的距离
A
Q
P
l
思考:两条平行线间的距离应该如何表示?
l1
l2
A
Q
P
二、点到之间的距离
A
Q
P
l
l1
l2
A
Q
P
平行线间距离
点到直线距离
【典型例题一】
例1 已知直线 l 经过点A(2,3,1),若向量u=(1,0,-1)是直线 l 的方向向量,则点P(4,3,2)到 l 的距离为_____
A
P
l
Q
【典型例题一】
变式 已知直线 l 经过点A(2,3,1),若向量n=(1,0,-1)所在直线与 l 垂直,则点P(4,3,2)到 l 的距离为_____
A
P
l
Q
n
如何用空间向量求点到平面的距离?
A
Q
P
l
α
三、点到平面的距离
A
Q
P
α
P
l
α
β
思考:直线和平面平行,则线面距离如何求解?
两个平行平面的距离呢?
三、点到平面的距离
A
Q
P
α
P
l
α
β
平行的线面距离
点到平面距离
平行的平面距离
【典型例题二】
例2 已知平面α的一个法向量n=(-2,-2,1),点A(-1,3,0)在α内,则P(-2,1,4)到α的距离为( )
答案: D
【典型例题二】
练习 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离。
A1
B1
C1
D1
A
D
C
B
E
F
x
z
y
【典型例题二】
练习 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离。
A1
B1
C1
D1
A
D
C
B
E
F
x
z
y
课堂小结
