人教B版高中数学选择性必修第一册1.2.3直线与平面的夹角 课件(共19张PPT)
文档属性
| 名称 | 人教B版高中数学选择性必修第一册1.2.3直线与平面的夹角 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 12:03:15 | ||
图片预览



文档简介
(共19张PPT)
1.2.3 直线与平面的夹角
主讲:
人教B版选择性必修第一册
第1章 空间向量
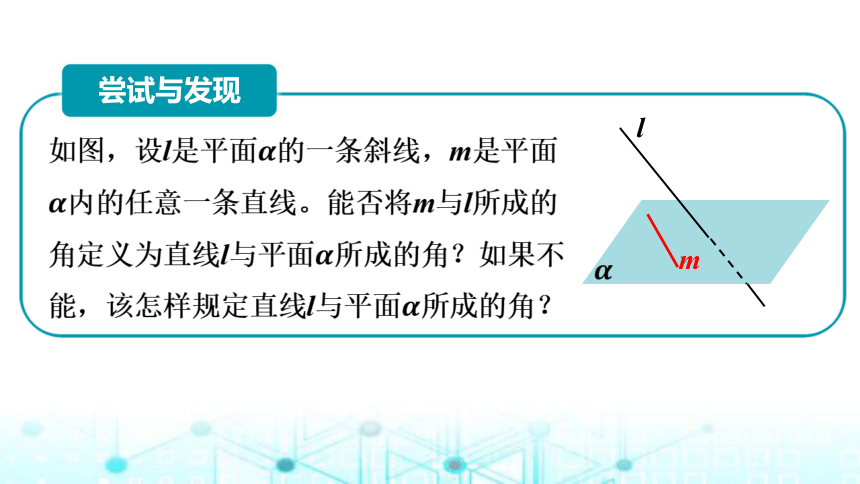
日常生活中,很多场景中都有直线与平面成一定角度的形象。
例如,在握笔写字时,如果把笔抽象成直线,把纸抽象成平面,则直线与平面成一定角度。
那么,怎样来刻画直线与平面所成的角呢?
l
m
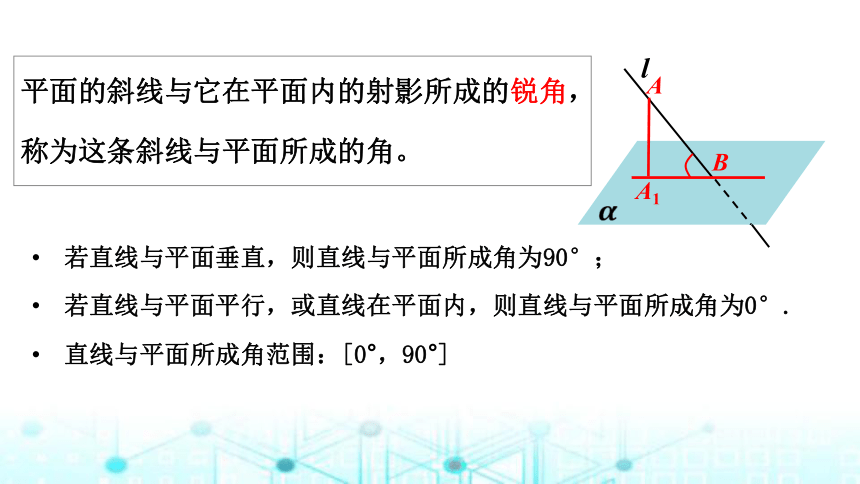
平面的斜线与它在平面内的射影所成的锐角,
称为这条斜线与平面所成的角。
一、直线与平面的夹角
l
A1
A
B
若直线与平面垂直,则直线与平面所成角为90°;
若直线与平面平行,或直线在平面内,则直线与平面所成角为0°.
直线与平面所成角范围:[0°,90°]
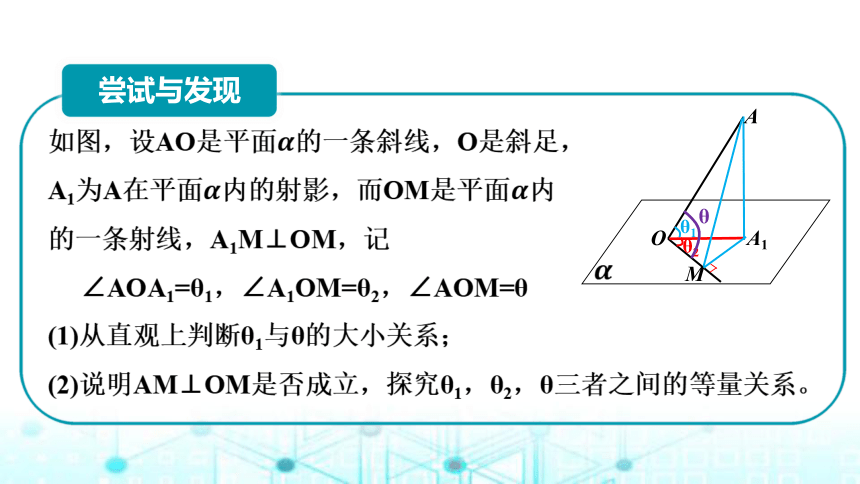
M
O
A
A1
θ1
θ2
θ
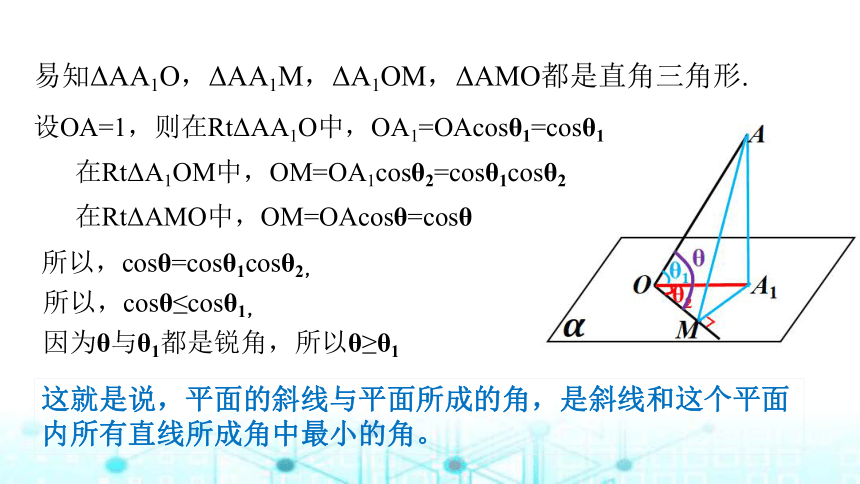
易知ΔAA1O,ΔAA1M,ΔA1OM,ΔAMO都是直角三角形.
设OA=1,则在RtΔAA1O中,OA1=OAcosθ1=cosθ1
在RtΔA1OM中,OM=OA1cosθ2=cosθ1cosθ2
在RtΔAMO中,OM=OAcosθ=cosθ
所以,cosθ=cosθ1cosθ2,
所以,cosθ≤cosθ1,
因为θ与θ1都是锐角,所以θ≥θ1
这就是说,平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角。
【典型例题一】
C
A
P
M
B
如何用空间向量求两条直线的夹角?
两条直线l1,l2夹角的范围:
如何用空间向量求直线与平面的夹角?
l
l
l
l
如何用空间向量求直线与平面的夹角?
l
l
二、用空间向量求直线与平面的夹角
l
l
A
B
A
B
【典型例题二】
例2. 已知ABCD-A1B1C1D1是正方体,求B1D1与平面A1BCD1所成角的大小.
化为向量问题
进行向量运算
回到图形问题
【典型例题二】
练习. 如图,在长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1=2,
M是AB的中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,求直线CD与平面MCA1所成角的正弦值。
【典型例题二】
解:因为AB=4, BC=3, CC1=2, M是AB的中点,
所以M(3,2,0), C(0,4,0), A1(3,0,2),D(0,0,0).
设n=(x,y,z)是平面MCA1的法向量,
取z =3, 则x=2, y=3,则n=(2,3,3)
当堂练习
×
×
当堂练习
A
当堂练习
课堂小结
1.2.3 直线与平面的夹角
主讲:
人教B版选择性必修第一册
第1章 空间向量
日常生活中,很多场景中都有直线与平面成一定角度的形象。
例如,在握笔写字时,如果把笔抽象成直线,把纸抽象成平面,则直线与平面成一定角度。
那么,怎样来刻画直线与平面所成的角呢?
l
m
平面的斜线与它在平面内的射影所成的锐角,
称为这条斜线与平面所成的角。
一、直线与平面的夹角
l
A1
A
B
若直线与平面垂直,则直线与平面所成角为90°;
若直线与平面平行,或直线在平面内,则直线与平面所成角为0°.
直线与平面所成角范围:[0°,90°]
M
O
A
A1
θ1
θ2
θ
易知ΔAA1O,ΔAA1M,ΔA1OM,ΔAMO都是直角三角形.
设OA=1,则在RtΔAA1O中,OA1=OAcosθ1=cosθ1
在RtΔA1OM中,OM=OA1cosθ2=cosθ1cosθ2
在RtΔAMO中,OM=OAcosθ=cosθ
所以,cosθ=cosθ1cosθ2,
所以,cosθ≤cosθ1,
因为θ与θ1都是锐角,所以θ≥θ1
这就是说,平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角。
【典型例题一】
C
A
P
M
B
如何用空间向量求两条直线的夹角?
两条直线l1,l2夹角的范围:
如何用空间向量求直线与平面的夹角?
l
l
l
l
如何用空间向量求直线与平面的夹角?
l
l
二、用空间向量求直线与平面的夹角
l
l
A
B
A
B
【典型例题二】
例2. 已知ABCD-A1B1C1D1是正方体,求B1D1与平面A1BCD1所成角的大小.
化为向量问题
进行向量运算
回到图形问题
【典型例题二】
练习. 如图,在长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1=2,
M是AB的中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,求直线CD与平面MCA1所成角的正弦值。
【典型例题二】
解:因为AB=4, BC=3, CC1=2, M是AB的中点,
所以M(3,2,0), C(0,4,0), A1(3,0,2),D(0,0,0).
设n=(x,y,z)是平面MCA1的法向量,
取z =3, 则x=2, y=3,则n=(2,3,3)
当堂练习
×
×
当堂练习
A
当堂练习
课堂小结
