人教B版高中数学选择性必修第一册2.2.1直线的倾斜角与斜率 课件(共15张PPT)
文档属性
| 名称 | 人教B版高中数学选择性必修第一册2.2.1直线的倾斜角与斜率 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
2.2.1 直线的倾斜角与斜率
主讲:张明明
人教B版选择性必修第一册
第2章 平面解析几何
我们知道,经过平面直角坐标系中的一点,可以有无数条不同的直线.
O
x
y
过同一点的直线l1,l2,l3,l4,它们彼此之间的不同点是什么?你能找到一个量来描述它们的不同点吗?你找到的量,能够使得图中任意两条不同的直线都有不同的取值吗?
倾斜角:一般地,给定平面直角坐标系中的一条直线,如果这条直线与x轴相交,将x轴绕着它们的交点按逆时针方向旋转到与直线重合时所转的最小正角记为θ,则称θ为这条直线的倾斜角。
一、倾斜角
l
x
y
O
θ
当直线 l 与x轴平行或重合时,规定倾斜角为0°
0°≤ θ <180°
倾斜角θ 的范围:
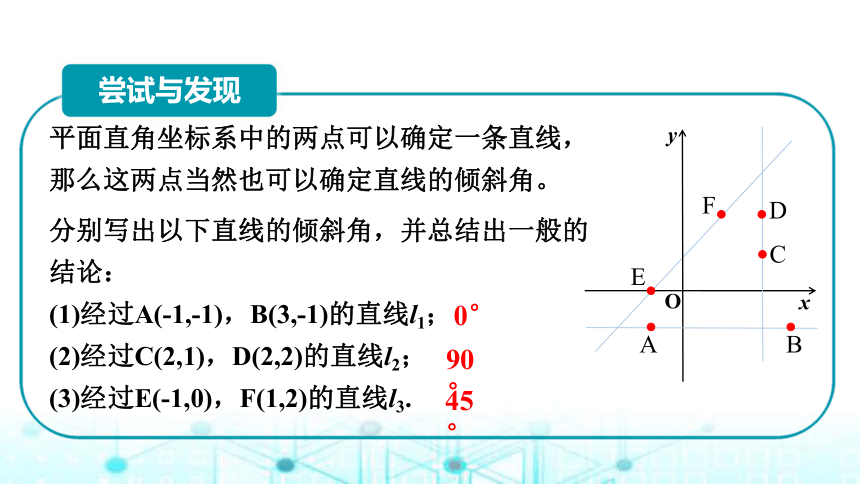
平面直角坐标系中的两点可以确定一条直线,那么这两点当然也可以确定直线的倾斜角。
O
x
y
分别写出以下直线的倾斜角,并总结出一般的结论:
(1)经过A(-1,-1),B(3,-1)的直线l1;
(2)经过C(2,1),D(2,2)的直线l2;
(3)经过E(-1,0),F(1,2)的直线l3.
A
B
C
D
E
F
0°
90°
45°
二、斜率
二、斜率
一般地,如果直线l的倾斜角为θ,
则当θ≠90°时,称 k = tan θ 为直线l的斜率;
当θ=90°时,称直线l的斜率不存在.
【典型例题一】
例1 已知直线l经过点A(-1,3)与B(2,0),求直线l的斜率k与倾斜角θ.
【典型例题二】
例2 已知平面直角坐标系中的四条直线l1,l2,l3,l4,如图所示,设它们的倾斜角分别为θ1,θ2,θ3,θ4,而且斜率分别为k1,k2,k3,k4. 分别将倾斜角和斜率按照从小到大的顺序排列.
O
x
y
l1
l2
l3
l4
【典型例题三】
例3 已知A(-2,-1),B(0,-3),C(1,-4),D(2,-6),则A,B,C共线吗?A,B,D呢?
三、直线的方向向量
一般地,如果表示非零向量a的有向线段所在的直线与直线l平行或重合,则称向量a为直线l的一个方向向量,记作a//l.
(1)如图所示,如果a=(-1,1)为直线 l 的一个方向向量,你能写出 l 的斜率k和倾斜角θ吗?
(2)一般地,如果已知向量a=(u,v)为直线l的一个方向向量,你能由此写出l的斜率k和倾斜角θ吗?
l
x
y
O
θ
a
三、直线的方向向量
一般地,如果表示非零向量a的有向线段所在的直线与直线l平行或重合,则称向量a为直线l的一个方向向量,记作a//l.
a
【典型例题四】
四、直线的法向量
一般地,如果表示非零向量v的有向线段所在的直线与直线l平行或重合,则称向量v为直线l的一个法向量,记作v⊥l.
v
显然,直线的方向向量与法向量相互垂直。
特别地,当x0与y0不全为0时,
若向量(x0,y0)是直线l的方向向量,则向量(y0,-x0)是直线l的法向量.
【典型例题五】
例5 已知a=(1,2)是直线l的一个方向向量,则直线l的一个法向量是v=_________
(2,-1)
2.2.1 直线的倾斜角与斜率
主讲:张明明
人教B版选择性必修第一册
第2章 平面解析几何
我们知道,经过平面直角坐标系中的一点,可以有无数条不同的直线.
O
x
y
过同一点的直线l1,l2,l3,l4,它们彼此之间的不同点是什么?你能找到一个量来描述它们的不同点吗?你找到的量,能够使得图中任意两条不同的直线都有不同的取值吗?
倾斜角:一般地,给定平面直角坐标系中的一条直线,如果这条直线与x轴相交,将x轴绕着它们的交点按逆时针方向旋转到与直线重合时所转的最小正角记为θ,则称θ为这条直线的倾斜角。
一、倾斜角
l
x
y
O
θ
当直线 l 与x轴平行或重合时,规定倾斜角为0°
0°≤ θ <180°
倾斜角θ 的范围:
平面直角坐标系中的两点可以确定一条直线,那么这两点当然也可以确定直线的倾斜角。
O
x
y
分别写出以下直线的倾斜角,并总结出一般的结论:
(1)经过A(-1,-1),B(3,-1)的直线l1;
(2)经过C(2,1),D(2,2)的直线l2;
(3)经过E(-1,0),F(1,2)的直线l3.
A
B
C
D
E
F
0°
90°
45°
二、斜率
二、斜率
一般地,如果直线l的倾斜角为θ,
则当θ≠90°时,称 k = tan θ 为直线l的斜率;
当θ=90°时,称直线l的斜率不存在.
【典型例题一】
例1 已知直线l经过点A(-1,3)与B(2,0),求直线l的斜率k与倾斜角θ.
【典型例题二】
例2 已知平面直角坐标系中的四条直线l1,l2,l3,l4,如图所示,设它们的倾斜角分别为θ1,θ2,θ3,θ4,而且斜率分别为k1,k2,k3,k4. 分别将倾斜角和斜率按照从小到大的顺序排列.
O
x
y
l1
l2
l3
l4
【典型例题三】
例3 已知A(-2,-1),B(0,-3),C(1,-4),D(2,-6),则A,B,C共线吗?A,B,D呢?
三、直线的方向向量
一般地,如果表示非零向量a的有向线段所在的直线与直线l平行或重合,则称向量a为直线l的一个方向向量,记作a//l.
(1)如图所示,如果a=(-1,1)为直线 l 的一个方向向量,你能写出 l 的斜率k和倾斜角θ吗?
(2)一般地,如果已知向量a=(u,v)为直线l的一个方向向量,你能由此写出l的斜率k和倾斜角θ吗?
l
x
y
O
θ
a
三、直线的方向向量
一般地,如果表示非零向量a的有向线段所在的直线与直线l平行或重合,则称向量a为直线l的一个方向向量,记作a//l.
a
【典型例题四】
四、直线的法向量
一般地,如果表示非零向量v的有向线段所在的直线与直线l平行或重合,则称向量v为直线l的一个法向量,记作v⊥l.
v
显然,直线的方向向量与法向量相互垂直。
特别地,当x0与y0不全为0时,
若向量(x0,y0)是直线l的方向向量,则向量(y0,-x0)是直线l的法向量.
【典型例题五】
例5 已知a=(1,2)是直线l的一个方向向量,则直线l的一个法向量是v=_________
(2,-1)
