河南省郑州市第57中学2024-2025学年新七年级入学摸底分班数学试卷(无答案)
文档属性
| 名称 | 河南省郑州市第57中学2024-2025学年新七年级入学摸底分班数学试卷(无答案) | 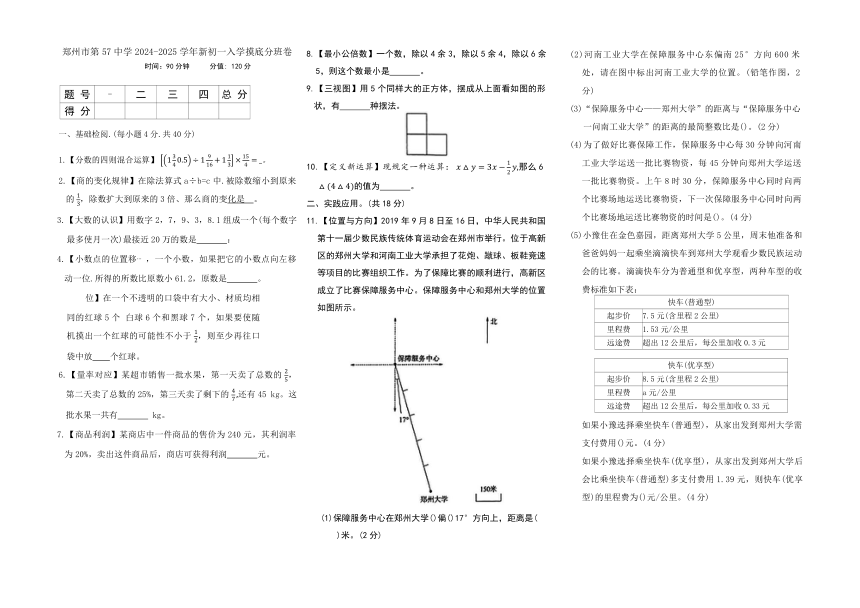 | |
| 格式 | docx | ||
| 文件大小 | 58.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 17:57:14 | ||
图片预览

文档简介
郑州市第57中学2024-2025学年新初一入学摸底分班卷
时间:90分钟 分值: 120分
题 号 一 二 三 四 总 分
得 分
一、基础检阅.(每小题4分.共40分)
1.【分数的四则混合运算】
2.【商的变化规律】在除法算式a÷b=c中.被除数缩小到原来的 ,除数扩大到原来的3倍、那么商的变化是 。
3.【大数的认识】用数字2,7,9、3,8.1组成一个(每个数字最多使月一次)最接近20万的数是 :
4.【小数点的位置移 ,一个小数,如果把它的小数点向左移动一位.所得的所数比原数小61.2,原数是 。
位】在一个不透明的口袋中有大小、材质均相同的红球5个 白球6个和黑球7个,如果要使随机摸出一个红球的可能性不小于 ,则至少再往口袋中放 个红球。
6.【量率对应】某超市销售一批水果,第一天卖了总数的 ,第二天卖了总数的25%,第三天卖了剩下的 还有45 kg。这批水果一共有 kg。
7.【商品利润】某商店中一件商品的售价为240元,其利润率为20%,卖出这件商品后,商店可获得利润 元。
8.【最小公倍数】一个数,除以4余3,除以5余4,除以6余5,则这个数最小是 。
9.【三视图】用5个同样大的正方体,摆成从上面看如图的形状,有 种摆法。
10.【定义新运算】现规定一种运算: 那么6 的值为 。
二、实践应用。(共18分)
11.【位置与方向】2019年9月8日至16日,中华人民共和国第十一届少数民族传统体育运动会在郑州市举行。位于高新区的郑州大学和河南工业大学承担了花炮、蹴球、板鞋竞速等项目的比赛组织工作。为了保障比赛的顺利进行,高新区成立了比赛保障服务中心。保障服务中心和郑州大学的位置如图所示。
(1)保障服务中心在郑州大学()偏()17°方向上,距离是( )米。(2分)
(2)河南工业大学在保障服务中心东偏南25°方向600米处,请在图中标出河南工业大学的位置。(铅笔作图,2分)
(3)“保障服务中心——郑州大学”的距离与“保障服务中心一问南工业大学”的距离的最简整数比是()。(2分)
(4)为了做好比赛保障工作,保障服务中心每30分钟向河南工业大学运送一批比赛物资,每45分钟向郑州大学运送一批比赛物资。上午8时30分,保障服务中心同时向两个比赛场地运送比赛物资,下一次保障服务中心同时向两个比赛场地运送比赛物资的时间是()。(4分)
(5)小豫住在金色嘉园,距离郑州大学5公里,周末他准备和爸爸妈妈一起乘坐滴滴快车到郑州大学观看少数民族运动会的比赛。滴滴快车分为普通型和优享型,两种车型的收费标准如下表:
快车(普通型)
起步价 7.5元(含里程2公里)
里程费 1.53元/公里
远途费 超出12公里后,每公里加收0.3元
快车(优享型)
起步价 8.5元(含里程2公里)
里程费 a元/公里
远途费 超出12公里后,每公里加收0.33元
如果小豫选择乘坐快车(普通型),从家出发到郑州大学需支付费用()元。(4分)
如果小豫选择乘坐快车(优享型),从家出发到郑州大学后会比乘坐快车(普通型)多支付费用1.39元,则快车(优享型)的里程费为()元/公里。(4分)
三、能力提升、(每小题5分,共30分)
12.【乘法分配律】 。
13.【底高模型】如图,三角形ABC 的面积是 三角形 BDE 的面积是 ( c m^{2}。
14.【三角形的基本性质】在一个平面内把12根同样长的火柴棒首尾相接.围成一个等腰三角形(火柴棒都要用上)、最多能围成 种不同的等腰三角形(含等边三角形)。
15.【三角形的面积】如图. 厘米, 厘米, 厘米,阴影部分的面积是144平方厘米,那么DE 等于 厘米。
16.【工程问题】一项工程,由甲队和乙队共同施工,12天可以完成;如果由甲队和丙队共同施工,15天可以完成;如果单独由甲队施工,20天可以完成;如果由甲队、乙队和丙队共同施工,那么 天可以完成。
17.【三角形的面积】如图,三角形ABC的周长为40cm,P点为其内部一点,且点 P 到三边的距离均为3cm,则三角形ABC 的面积为 ( c m^{2}。
四、思维挑战。(每空4分,共32分)
18.【数形规律】在底面积为 100平方厘米的长方体水槽内放入一个长方体量杯(如图1),以恒定不变的速度先向量杯中注水,注满量杯后,继续注水,直至注满水槽为止。此过程中,量杯本身的质量和体积忽略不计,量杯在大水槽中的位置始终不变,水槽中水面上升的高度h(厘米)与注水时间t(秒)之间的关系如图2所示。
(1)将量杯注满水所用的时间是 秒。
(2)量杯的底面积是 平方厘米。
(3)如果注满水槽所用的时间为180 秒,则水槽的高为 厘米。
19.【数列创新问题】阅读下列材料,回答问题。
2019年10月29日,第二届世界顶尖科学家论坛开幕,全球顶尖科学家汇聚上海,共同探讨科学发展前沿问题。本届大会还邀请了青少年科学家参加,最年轻的一位“小小科学家”,是来自华东师大二附中高一年级年仅15岁的谈方琳同学,她的研究成果是斐波那契数列与贝祖数的估计。
斐波那契数列是一个很有意思的数列,我们一起来研究一下吧!
(1)斐波那契数列(Fibonacci sequence)指的是这样一个数列:
1,1,2,3,5,8,13,21,34, A , B , C . D ,…,这个数列在D处的值应该是 。
有趣的是,当我们根据发现的规律不断往后写出各项时,随着数列项数的增加,其前一项与后一项的比值越来越逼近黄金分割(近似为0.618)。
(2)如果斐波那契数列的第m项的值为75025,则第(m-1)项与第(m+1)项的和最接近 。
A.130000 B.150000 C.170000 D.190000
如果我们把斐波那契数列各项的个位上的数按顺序记录下来,会发现它是一个60步的循环:
11235,83145,94370,77415,61785,38190,
99875,27965,16730,33695,49325,72910,
11235,83145,94370,77415,61785,38190,
99875,27965,16730,33695,49325,72910,
(3)根据上述规律,斐波那契数列第2019 项的个位上的数是 。
(4)斐波那契数列第1000项到第2019项(含第 1000 项和第2019项)中,个位上是0的项的个数总共有 个。
三角形的三边关系定理和斐波那契数列也有着某种联系,通过解决下面的问题,相信你能够发现。
(5)现有长为143厘米的铁丝,要截成n小段(n>2),每段的长度都是整厘米数且都不小于1厘米,如果其中任意三小段都不能拼成三角形,那么n的最大值为 。
时间:90分钟 分值: 120分
题 号 一 二 三 四 总 分
得 分
一、基础检阅.(每小题4分.共40分)
1.【分数的四则混合运算】
2.【商的变化规律】在除法算式a÷b=c中.被除数缩小到原来的 ,除数扩大到原来的3倍、那么商的变化是 。
3.【大数的认识】用数字2,7,9、3,8.1组成一个(每个数字最多使月一次)最接近20万的数是 :
4.【小数点的位置移 ,一个小数,如果把它的小数点向左移动一位.所得的所数比原数小61.2,原数是 。
位】在一个不透明的口袋中有大小、材质均相同的红球5个 白球6个和黑球7个,如果要使随机摸出一个红球的可能性不小于 ,则至少再往口袋中放 个红球。
6.【量率对应】某超市销售一批水果,第一天卖了总数的 ,第二天卖了总数的25%,第三天卖了剩下的 还有45 kg。这批水果一共有 kg。
7.【商品利润】某商店中一件商品的售价为240元,其利润率为20%,卖出这件商品后,商店可获得利润 元。
8.【最小公倍数】一个数,除以4余3,除以5余4,除以6余5,则这个数最小是 。
9.【三视图】用5个同样大的正方体,摆成从上面看如图的形状,有 种摆法。
10.【定义新运算】现规定一种运算: 那么6 的值为 。
二、实践应用。(共18分)
11.【位置与方向】2019年9月8日至16日,中华人民共和国第十一届少数民族传统体育运动会在郑州市举行。位于高新区的郑州大学和河南工业大学承担了花炮、蹴球、板鞋竞速等项目的比赛组织工作。为了保障比赛的顺利进行,高新区成立了比赛保障服务中心。保障服务中心和郑州大学的位置如图所示。
(1)保障服务中心在郑州大学()偏()17°方向上,距离是( )米。(2分)
(2)河南工业大学在保障服务中心东偏南25°方向600米处,请在图中标出河南工业大学的位置。(铅笔作图,2分)
(3)“保障服务中心——郑州大学”的距离与“保障服务中心一问南工业大学”的距离的最简整数比是()。(2分)
(4)为了做好比赛保障工作,保障服务中心每30分钟向河南工业大学运送一批比赛物资,每45分钟向郑州大学运送一批比赛物资。上午8时30分,保障服务中心同时向两个比赛场地运送比赛物资,下一次保障服务中心同时向两个比赛场地运送比赛物资的时间是()。(4分)
(5)小豫住在金色嘉园,距离郑州大学5公里,周末他准备和爸爸妈妈一起乘坐滴滴快车到郑州大学观看少数民族运动会的比赛。滴滴快车分为普通型和优享型,两种车型的收费标准如下表:
快车(普通型)
起步价 7.5元(含里程2公里)
里程费 1.53元/公里
远途费 超出12公里后,每公里加收0.3元
快车(优享型)
起步价 8.5元(含里程2公里)
里程费 a元/公里
远途费 超出12公里后,每公里加收0.33元
如果小豫选择乘坐快车(普通型),从家出发到郑州大学需支付费用()元。(4分)
如果小豫选择乘坐快车(优享型),从家出发到郑州大学后会比乘坐快车(普通型)多支付费用1.39元,则快车(优享型)的里程费为()元/公里。(4分)
三、能力提升、(每小题5分,共30分)
12.【乘法分配律】 。
13.【底高模型】如图,三角形ABC 的面积是 三角形 BDE 的面积是 ( c m^{2}。
14.【三角形的基本性质】在一个平面内把12根同样长的火柴棒首尾相接.围成一个等腰三角形(火柴棒都要用上)、最多能围成 种不同的等腰三角形(含等边三角形)。
15.【三角形的面积】如图. 厘米, 厘米, 厘米,阴影部分的面积是144平方厘米,那么DE 等于 厘米。
16.【工程问题】一项工程,由甲队和乙队共同施工,12天可以完成;如果由甲队和丙队共同施工,15天可以完成;如果单独由甲队施工,20天可以完成;如果由甲队、乙队和丙队共同施工,那么 天可以完成。
17.【三角形的面积】如图,三角形ABC的周长为40cm,P点为其内部一点,且点 P 到三边的距离均为3cm,则三角形ABC 的面积为 ( c m^{2}。
四、思维挑战。(每空4分,共32分)
18.【数形规律】在底面积为 100平方厘米的长方体水槽内放入一个长方体量杯(如图1),以恒定不变的速度先向量杯中注水,注满量杯后,继续注水,直至注满水槽为止。此过程中,量杯本身的质量和体积忽略不计,量杯在大水槽中的位置始终不变,水槽中水面上升的高度h(厘米)与注水时间t(秒)之间的关系如图2所示。
(1)将量杯注满水所用的时间是 秒。
(2)量杯的底面积是 平方厘米。
(3)如果注满水槽所用的时间为180 秒,则水槽的高为 厘米。
19.【数列创新问题】阅读下列材料,回答问题。
2019年10月29日,第二届世界顶尖科学家论坛开幕,全球顶尖科学家汇聚上海,共同探讨科学发展前沿问题。本届大会还邀请了青少年科学家参加,最年轻的一位“小小科学家”,是来自华东师大二附中高一年级年仅15岁的谈方琳同学,她的研究成果是斐波那契数列与贝祖数的估计。
斐波那契数列是一个很有意思的数列,我们一起来研究一下吧!
(1)斐波那契数列(Fibonacci sequence)指的是这样一个数列:
1,1,2,3,5,8,13,21,34, A , B , C . D ,…,这个数列在D处的值应该是 。
有趣的是,当我们根据发现的规律不断往后写出各项时,随着数列项数的增加,其前一项与后一项的比值越来越逼近黄金分割(近似为0.618)。
(2)如果斐波那契数列的第m项的值为75025,则第(m-1)项与第(m+1)项的和最接近 。
A.130000 B.150000 C.170000 D.190000
如果我们把斐波那契数列各项的个位上的数按顺序记录下来,会发现它是一个60步的循环:
11235,83145,94370,77415,61785,38190,
99875,27965,16730,33695,49325,72910,
11235,83145,94370,77415,61785,38190,
99875,27965,16730,33695,49325,72910,
(3)根据上述规律,斐波那契数列第2019 项的个位上的数是 。
(4)斐波那契数列第1000项到第2019项(含第 1000 项和第2019项)中,个位上是0的项的个数总共有 个。
三角形的三边关系定理和斐波那契数列也有着某种联系,通过解决下面的问题,相信你能够发现。
(5)现有长为143厘米的铁丝,要截成n小段(n>2),每段的长度都是整厘米数且都不小于1厘米,如果其中任意三小段都不能拼成三角形,那么n的最大值为 。
同课章节目录
