2025年新九年级数学人教版暑假大讲堂第七讲 21.3 实际问题与一元二次方程(二)(学生版+解析版)
文档属性
| 名称 | 2025年新九年级数学人教版暑假大讲堂第七讲 21.3 实际问题与一元二次方程(二)(学生版+解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-27 16:21:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年新九年级数学人教版暑假大讲堂
第七讲 实际问题与一元二次方程(二)
知识点梳理
知识点1 与图形有关的问题
与图形有关的问题通常涉及面积、周长、边长等几何量的计算。这类问题可能需要利用一元二次方程来求解。例如,已知矩形的面积和一边长,求另一边长;或者知道三角形的两边长和第三边的方程,求三角形的周长等。
要点诠释:
面积问题应注意三点:
(1)图形的面积公式是基本的等量关系
(2)利用平移的性质把零散的图形拼接在一起
(3)取舍根时注意图形中边长的限制。
知识点2 动态几何问题
动态几何问题涉及图形在运动或变化过程中的性质。这类问题可能需要通过一元二次方程来描述图形的运动轨迹或变化规律。例如,一个点在一个圆上运动,其到圆心的距离与运动时间的关系可能符合一元二次方程。
要点诠释:
(1)明确动点的运动方向、速度及终止条件(如到达终点停止),将运动过程分段处理。分阶段计算。
(2)注意时间变量的取值范围
知识点3 图形图表信息问题
一元二次方程实际问题中图表信息问题的解题要点主要包括以下几个步骤 :
分析题意,找到题中未知数和题给条件的相等关系 :首先,需要仔细阅读题目,理解题目中的条件和要求,明确需要求解的未知数。然后,找出题目中给出的条件与未知数之间的关系,通常这种关系可以通过等式来表示。
设未知数,并用所设的未知数的代数式表示其余的未知数 :根据找到的相等关系,设定一个或多个未知数。然后,用这些未知数表示题目中给出的其他数值或条件。
找出相等关系,并用它列出方程 :根据设定的未知数和找到的相等关系,列出包含这些未知数的等式。这个等式就是一元二次方程。
解方程求出题中未知数的值 :使用代数方法解这个一元二次方程,求出未知数的值。这一步可能需要使用配方法、公式法等方法。
检验所求的答案是否符合题意 :最后,将求得的答案代入原问题中进行检验,确保答案符合题目的所有条件。
题型1 图形面积问题
【例1】.如图,某校课外生物小组的试验园地是长32米 宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为578平方米,则小道的宽为多少米
针对训练1
1.某园林公司举行盆景展览,如图所示是用这两种盆景摆成的图案,黑色圆点为六月雪盆景,黑色正方形为九里香盆景.图1中六月雪盆景数量为4,九里香盆景数量为2;图2中六月雪盆景数量为6,九里香盆景数量为6;图3中六月雪盆景数量为8,九里香盆景数量为12;…
按照以上规律,解决下列问题:
(1)图5中,六月雪盆景数量为_______,九里香盆景数量为_______;
(2)若园林公司用这两种盆景共132盆按如上规律摆成一个图案,请求出该图案中六月雪和九里香这两种盆景分别多少盆?
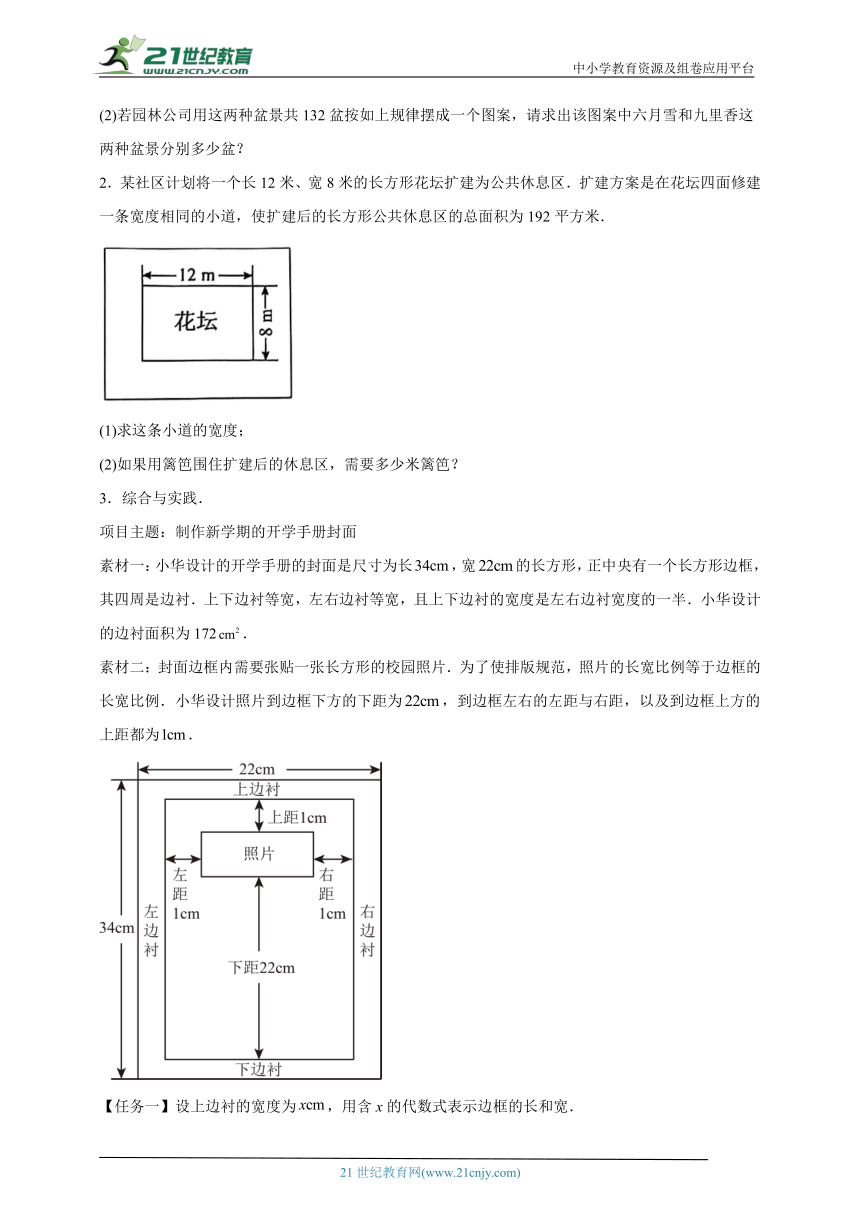
2.某社区计划将一个长12米、宽8米的长方形花坛扩建为公共休息区.扩建方案是在花坛四面修建一条宽度相同的小道,使扩建后的长方形公共休息区的总面积为192平方米.
(1)求这条小道的宽度;
(2)如果用篱笆围住扩建后的休息区,需要多少米篱笆?
3.综合与实践.
项目主题:制作新学期的开学手册封面
素材一:小华设计的开学手册的封面是尺寸为长,宽的长方形,正中央有一个长方形边框,其四周是边衬.上下边衬等宽,左右边衬等宽,且上下边衬的宽度是左右边衬宽度的一半.小华设计的边衬面积为172.
素材二:封面边框内需要张贴一张长方形的校园照片.为了使排版规范,照片的长宽比例等于边框的长宽比例.小华设计照片到边框下方的下距为,到边框左右的左距与右距,以及到边框上方的上距都为.
【任务一】设上边衬的宽度为,用含x的代数式表示边框的长和宽.
【任务二】求边框的长和宽.
【任务三】通过计算说明,小华的设计是否规范.
4.根据以下素材,探索完成任务.
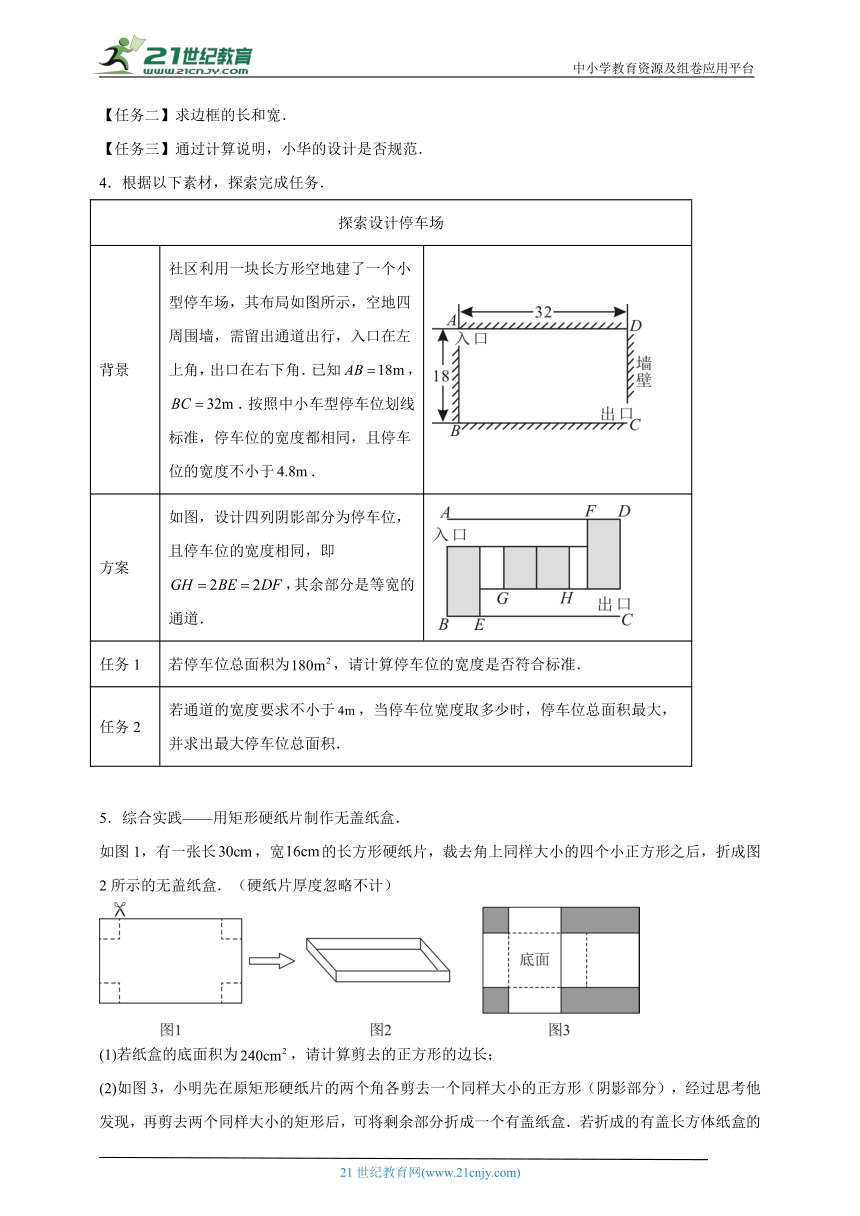
探索设计停车场
背景 社区利用一块长方形空地建了一个小型停车场,其布局如图所示,空地四周围墙,需留出通道出行,入口在左上角,出口在右下角.已知,.按照中小车型停车位划线标准,停车位的宽度都相同,且停车位的宽度不小于.
方案 如图,设计四列阴影部分为停车位,且停车位的宽度相同,即,其余部分是等宽的通道.
任务1 若停车位总面积为,请计算停车位的宽度是否符合标准.
任务2 若通道的宽度要求不小于,当停车位宽度取多少时,停车位总面积最大,并求出最大停车位总面积.
5.综合实践——用矩形硬纸片制作无盖纸盒.
如图1,有一张长,宽的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图2所示的无盖纸盒.(硬纸片厚度忽略不计)
(1)若纸盒的底面积为,请计算剪去的正方形的边长;
(2)如图3,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒.若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
题型2 动态几何问题
【例2】.如图,在中,,,,动点 P从点 A 出发沿边向点B以的速度移动,同时动点Q从点 B 出发沿边向点 C 以的速度移动,当 P 运动到 B 点时 P、Q 两点同时停止运动,设运动时间为.
(1) ; ;(用t的代数式表示)
(2)D是的中点,连接、,t为何值时的面积为?
针对训练2
1.如图所示,在四边形中,,,,动点从点出发沿AD方向向点以的速度运动,动点从点开始沿着方向向点以的速度运动.点分别从点和点同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)当运动秒时,线段__________(用含有t的代数式表示)
(2)经过多长时间,四边形是矩形?
(3)经过多长时间,PQ的长为?
2.如图,在矩形中,,,点从点开始以的速度沿边向移动,点从点开始以的速度沿边向点移动.如果、分别从、同时出发,设移动的时间为t. 求:
(1)当t为多少时,的面积等于?
(2)当t为多少时,是以为斜边的直角三角形?
3.如图,在中,,动点从点出发,沿向点以的速度匀速运动,另一动点从点出发,沿向点以的速度匀速运动,点同时出发,当有一点到达终点时,另一点也同时停止运动,设运动时间为,那么经过多长时间,的面积为?
4.综合与实践
如图1,在矩形中,,动点P,Q分别以的速度从点A,B同时出发,点P沿着运动到点B时停止,点Q沿着运动到点A时停止.设运动时间为.
(1)当点P在上运动时, ________, ________;(用含t的代数式表示)
(2)在(1)的条件下,当时,求t的值;
(3)如图2、图3,点P沿着运动到点B的过程中、当的面积为时,求t的值.
5.如图,菱形中, 交于点 O, ,动点 M 从 A 点出发沿方向以匀速直线运动到 C 点,动点 N 从 B 点出发沿方向以匀速直线运动到 D 点.若 M,N 同时出发,设运动时间为 t 秒:
(1)当时, , .(用 t 表示)
(2)当秒时, 的面积为多少?
(3)点 M 到达点 C 后立即原路返回,速度保持不变,直到点 N 到达 D 后同时停止运动,那么在整个移 动过程中,是否存在某一时刻,使得的面积为?若存在,求出运动时间;若不存在,请说 明理由.
题型3 图表信息问题
【例3】.某商店购进800个旅游纪念品,进价为每个50元,第一周以每个80元的价格售出200个,第二周若按每个80元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出10个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品以及清仓处理,以每个40元的价格全部售出,如果这批旅游纪念品共获利9000元.
(1)填表(结果需化简)
时间 第一周 第二周 清仓时
单价(元) 80 40
销售量(件) 200
(2)求第二周每个旅游纪念品的销售价格为多少元?
针对训练3
1.乌克兰危机发生之后,外交战线按照党中央的部署紧急行动,在战火粉飞中已将5200多名同胞安全从乌克兰撤离,电影《万里归途》正是“外交为民”的真实写照,如表是该影片票房的部分数据,(注:票房是指截止发布日期的所有售票累计收入)
影片《万里归途》的部分统计数据
发布日期 10月8日 10月11日 10月12日
发布次数 第1次 第2次 第3次
票房 10亿元 12.1亿元
(1)平均每次累计票房增长的百分率是多少?
(2)在(1)的条件下,若票价每张40元,求10月11日卖出多少张电影票
2.请阅读下列材料,并按要求完成相应的任务:
人类对一元二次方程的研究经历了漫长的岁月.一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中.到了中世纪,阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法,并用几何法进行了证明.我国古代三国时期的数学家赵爽也给出了类似的几何解法.赵爽在其所著的《勾股圆方图注》中记载了解方程即得方法.首先构造了如图1所示得图形,图中的大正方形面积是,其中四个全等的小矩形面积分别为,中间的小正方形面积为,所以大正方形的面积又可表示为,据此易得.
任务:
(1)参照上述图解一元二次方程的方法,请在下面三个构图中选择能够说明方程的正确构图是 (从序号①②③中选择).
(2)请你通过上述问题的学习,在图2的网格中设计正确的构图,用几何法求解方程(写出必要的思考过程).
3.小王某月手机话费中的各项费用统计情况见下列图所示,其中月功能费为5元,请你根据统计图的信息完成下列各题:
(1)该月小王手机话费共有________元.
(2)扇形统计图中,表示短信费的扇形的圆心角______度.
(3)请将条形统计图补充完整.
(4)电信公司为让利给用户,从下月起每月将对长途话费进行打折优惠,如果小王每月长途电话的通话时间不变,那么两个月后,月长途花费将降至28.8元,那么长途话费的月平均折扣为多少?
4.已知:p为实数.
p k q
… … …
3 16×3+26 2×2×6
4 16×4+26 2×3×7
5 16×5+26 2×4×8
6 16×6+26 2×5×9
7 16×7+26 2×6×10
… … …
根据上表中的规律,回答下列问题:
(1)当p为何值时,k=38
(2)当p为何值时,k与q的值相等?
5.某旅行社一则旅游消息如下:
旅游人数 收费标准
不超过人 人均收费元
超过人 每增加一人,人均收费减少元,但人均收费不低于元
(1)甲公司员工分两批参加该项旅游,分别支付给旅行社元和元,甲公司员工有__________人.
(2)乙公司员工一起参加该项旅游,支付给旅行社元,乙公司员工多少人?
能力提升 创新拓展
1.在数学综合与实践课上,李老师让同学们以“正方形折叠”为主题开展数学活动.
【具体操作】如图1,在正方形中,将沿过点的直线翻折,点落在正方形内部的点处,得到,折痕为;再将沿过点的直线翻折,使与重合,得到,折痕为.由以上操作,不难发现,,三点在同一条直线上.
【问题解决】
(1)请直接写出 ;
(2)若,,求正方形的边长;
【深入探究】
(3)如图2,再将沿所在直线折叠,点恰好落在线段的点处,得到,线段与相交于点,请写出,,三条线段的数量关系,并说明理由.
2.在日历上,我们可以发现其中某些数满足一定的规律,如图是2019年1月份的日历.我们任意选择其中所示的菱形框部分,将每个菱形框部分中去掉中间位置的数之后,相对的两对数分别相乘,再相减,例如:,.不难发现,结果都是48.
(1)请证明发现的规律;
(2)若用一个如图所示菱形框,再框出5个数字,其中最小数与最大数的积为435,求出这5个数中的最大数;
(3)嘉琪说:她用一个如图所示菱形框,框出5个数字,其中最小数与最大数的积是95,直接判断他的说法是否正确(不必叙述理由).
3.如图,在矩形中,,,点从点出发沿以的速度向点移动;同时,点从点出发沿以的速度向点移动,当其中一点到达终点运动即停止.设运动时间为秒.
(1)在运动过程中,的长度能否为?若能,求出的值,若不能,请说明理由;
(2)在运动过程中,的面积能否为?若能,求出的值,若不能,请说明理由;
(3)取的中点,运动过程中,当时,求的值.
2025年新九年级数学人教版暑假大讲堂
第七讲 实际问题与一元二次方程(二)(解析版)
知识点梳理
知识点1 与图形有关的问题
与图形有关的问题通常涉及面积、周长、边长等几何量的计算。这类问题可能需要利用一元二次方程来求解。例如,已知矩形的面积和一边长,求另一边长;或者知道三角形的两边长和第三边的方程,求三角形的周长等。
要点诠释:
面积问题应注意三点:
(1)图形的面积公式是基本的等量关系
(2)利用平移的性质把零散的图形拼接在一起
(3)取舍根时注意图形中边长的限制。
知识点2 动态几何问题
动态几何问题涉及图形在运动或变化过程中的性质。这类问题可能需要通过一元二次方程来描述图形的运动轨迹或变化规律。例如,一个点在一个圆上运动,其到圆心的距离与运动时间的关系可能符合一元二次方程。
要点诠释:
(1)明确动点的运动方向、速度及终止条件(如到达终点停止),将运动过程分段处理。分阶段计算。
(2)注意时间变量的取值范围
知识点3 图形图表信息问题
一元二次方程实际问题中图表信息问题的解题要点主要包括以下几个步骤 :
分析题意,找到题中未知数和题给条件的相等关系 :首先,需要仔细阅读题目,理解题目中的条件和要求,明确需要求解的未知数。然后,找出题目中给出的条件与未知数之间的关系,通常这种关系可以通过等式来表示。
设未知数,并用所设的未知数的代数式表示其余的未知数 :根据找到的相等关系,设定一个或多个未知数。然后,用这些未知数表示题目中给出的其他数值或条件。
找出相等关系,并用它列出方程 :根据设定的未知数和找到的相等关系,列出包含这些未知数的等式。这个等式就是一元二次方程。
解方程求出题中未知数的值 :使用代数方法解这个一元二次方程,求出未知数的值。这一步可能需要使用配方法、公式法等方法。
检验所求的答案是否符合题意 :最后,将求得的答案代入原问题中进行检验,确保答案符合题目的所有条件。
题型1 图形面积问题
【例1】.如图,某校课外生物小组的试验园地是长32米 宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为578平方米,则小道的宽为多少米
【答案】米.
【分析】本题考查了一元二次方程的应用面积问题,解题的关键是巧妙的运用等积代换.
设小道的宽为米,则长、宽分别为米、米,根据矩形的面积公式就可以列出方程,解方程即可.
【详解】解:设该小道的宽为米,依题意得
,
解得,.
因为,不合题意,舍去.
所以.
答:小道宽米.
针对训练1
1.某园林公司举行盆景展览,如图所示是用这两种盆景摆成的图案,黑色圆点为六月雪盆景,黑色正方形为九里香盆景.图1中六月雪盆景数量为4,九里香盆景数量为2;图2中六月雪盆景数量为6,九里香盆景数量为6;图3中六月雪盆景数量为8,九里香盆景数量为12;…
按照以上规律,解决下列问题:
(1)图5中,六月雪盆景数量为_______,九里香盆景数量为_______;
(2)若园林公司用这两种盆景共132盆按如上规律摆成一个图案,请求出该图案中六月雪和九里香这两种盆景分别多少盆?
【答案】(1)12;30
(2)六月雪盆景有22盆,九里香盆景有110盆
【分析】本题考查了图形规律探索、一元二次方程的应用,观察图形的变化找到隐含的规律是解题的关键.
(1)观察图形,得出第个图中六月雪盆景数量为,九里香盆景数量为,再代入即可求解;
(2)设该图案为如上规律的第个图,根据题意列出方程,解出的值,即可解答.
【详解】(1)解:图1中六月雪盆景数量为,九里香盆景数量为,
图2中六月雪盆景数量为,九里香盆景数量为,
图3中六月雪盆景数量为,九里香盆景数量为,
图4中六月雪盆景数量为,九里香盆景数量为,
…
第个图中六月雪盆景数量为,九里香盆景数量为,
当时,,,
图5中,六月雪盆景数量为12,九里香盆景数量为30.
故答案为:12;30.
(2)解:设该图案为如上规律的第个图,
由题意得,,
解得:,(不符合题意,舍去),
此时六月雪盆景数量为盆,九里香盆景数量为盆,
答:六月雪盆景有22盆,九里香盆景有110盆.
2.某社区计划将一个长12米、宽8米的长方形花坛扩建为公共休息区.扩建方案是在花坛四面修建一条宽度相同的小道,使扩建后的长方形公共休息区的总面积为192平方米.
(1)求这条小道的宽度;
(2)如果用篱笆围住扩建后的休息区,需要多少米篱笆?
【答案】(1)这条小道的宽度为2米
(2)需要56米篱笆
【分析】本题考查了一元二次方程的应用,找准等量关系,正确建立方程是解题关键.
(1)设这条小道的宽度为米,根据扩建后的长方形公共休息区的总面积为192平方米建立方程,解方程即可得;
(2)根据(1)的结果求出扩建后的长方形公共休息区的长与宽,再利用长方形的周长公式计算即可得.
【详解】(1)解:设这条小道的宽度为米,
由题意得:,
解得或(不符合题意,舍去),
答:这条小道的宽度为2米.
(2)解:由(1)可知,扩建后的长方形公共休息区的长为(米),宽为(米),
则(米),
答:如果用篱笆围住扩建后的休息区,需要56米篱笆.
3.综合与实践.
项目主题:制作新学期的开学手册封面
素材一:小华设计的开学手册的封面是尺寸为长,宽的长方形,正中央有一个长方形边框,其四周是边衬.上下边衬等宽,左右边衬等宽,且上下边衬的宽度是左右边衬宽度的一半.小华设计的边衬面积为172.
素材二:封面边框内需要张贴一张长方形的校园照片.为了使排版规范,照片的长宽比例等于边框的长宽比例.小华设计照片到边框下方的下距为,到边框左右的左距与右距,以及到边框上方的上距都为.
【任务一】设上边衬的宽度为,用含x的代数式表示边框的长和宽.
【任务二】求边框的长和宽.
【任务三】通过计算说明,小华的设计是否规范.
【答案】任务一:边框的长和宽为,;任务二:长和宽为与;任务三:设计符合规范,见解析
【分析】本题考查了一元二次方程的应用、列代数式以及有理数的混合运算,解题的关键是:根据各边之间的关系,用含的代数式表示出边框的长和宽;找准等量关系,正确列出一元二次方程;验证照片的长宽比例是否等于边框的长宽比例.
[任务一]设上边衬的宽度为,则下边衬的宽度为,左、右边衬的宽度为,利用边框的长上边衬的宽度下边衬的宽度及边框的宽左边衬的宽度又边衬的宽度,即可用含的代数式表示出边框的长和宽;
[任务二]根据小华设计的边衬面积为,可列出关于的一元二次方程,解之可得出的值,再将其符合题意的值代入及中,即可求出结论;
[任务三]求出照片的长、宽,结合照片的长宽比例等于边框的长宽比例,即可得出结论.
【详解】解:[任务一]设上边衬的宽度为,则下边衬的宽度为,左、右边衬的宽度为,
边框的长为,宽为;
[任务二]根据题意得:,
整理得:,
解得:,(不符合题意,舍去),
,
.
答:边框的长为,宽为;
[任务三]小华的设计规范,理由如下:
照片的长为,
照片的宽为,
边框的长为,宽为,且,
小华的设计规范.
4.根据以下素材,探索完成任务.
探索设计停车场
背景 社区利用一块长方形空地建了一个小型停车场,其布局如图所示,空地四周围墙,需留出通道出行,入口在左上角,出口在右下角.已知,.按照中小车型停车位划线标准,停车位的宽度都相同,且停车位的宽度不小于.
方案 如图,设计四列阴影部分为停车位,且停车位的宽度相同,即,其余部分是等宽的通道.
任务1 若停车位总面积为,请计算停车位的宽度是否符合标准.
任务2 若通道的宽度要求不小于,当停车位宽度取多少时,停车位总面积最大,并求出最大停车位总面积.
【答案】任务1:停车位的宽度符合标准;任务2:当停车位的宽度为时,停车位的总面积最大为
【分析】本题考查一元二次方程的实际应用,配方法的应用,读懂题意,正确的列出方程,是解题的关键:
任务1:设停车位的宽度为,通道的宽度为,根据图形可知:,进而得到,根据停车位总面积为,列出方程进行求解后,结合停车位的宽度不小于进行判断即可;
任务2:设停车位的总面积为,面积公式表示出,配方法求最值即可.
【详解】解:任务1:设停车位的宽度为,通道的宽度为,由图和题意可知:,
∴,
∵停车位总面积为,
∴,
把代入,得:,
解得:或(舍去);
∵,
∴停车位的宽度符合标准.
任务2:设停车位的总面积为,由任务1可知:,
∴
,
,
∵且,
∴,
∴当时,最大,
答:当停车位的宽度为时,停车位的总面积最大为.
5.综合实践——用矩形硬纸片制作无盖纸盒.
如图1,有一张长,宽的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图2所示的无盖纸盒.(硬纸片厚度忽略不计)
(1)若纸盒的底面积为,请计算剪去的正方形的边长;
(2)如图3,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒.若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
【答案】(1)
(2)
【分析】本题考查了一元二次方程的应用,理解题意,正确列出一元二次方程是解此题的关键.
(1)设减去的正方形的边长为,则纸盒底面长方形的长为,宽为,根据题意列出一元二次方程,解方程即可得出答案;
(2)设剪去的正方形的边长为,根据题意列出一元二次方程,解方程即可得出答案.
【详解】(1)解:设减去的正方形的边长为,则纸盒底面长方形的长为,宽为,
由题意得:,
解得:或(舍去),
∴剪去正方形的边长为;
(2)解:设剪去的正方形的边长为,
由题意得:,
解得:或(不符合题意,舍去),
∴剪去的正方形的边长为.
题型2 动态几何问题
【例2】.如图,在中,,,,动点 P从点 A 出发沿边向点B以的速度移动,同时动点Q从点 B 出发沿边向点 C 以的速度移动,当 P 运动到 B 点时 P、Q 两点同时停止运动,设运动时间为.
(1) ; ;(用t的代数式表示)
(2)D是的中点,连接、,t为何值时的面积为?
【答案】(1),
(2)或4
【分析】本题主要考查了一元二次方程的应用,解题的关键是读懂题意,找到关键描述语,列出等量关系.
(1)根据速度时间路程,列出代数式即可;
(2)过点D作于H,利用三角形中位线定理求得的长度;然后根据题意和三角形的面积列出方程,求出方程的解即可.
【详解】(1)根据题意得: ,,
,
故答案为:,.
(2)如图,过点D作于H,
∵,即,
∴,
又∵D是的中点,
∴,是的中位线,
∴,
根据题意,得,
整理,得,
解得:,,
当或4时,的面积是.
针对训练2
1.如图所示,在四边形中,,,,动点从点出发沿AD方向向点以的速度运动,动点从点开始沿着方向向点以的速度运动.点分别从点和点同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)当运动秒时,线段__________(用含有t的代数式表示)
(2)经过多长时间,四边形是矩形?
(3)经过多长时间,PQ的长为?
【答案】(1)t,
(2)
(3)经过5秒或9秒,的长为
【分析】此题主要考查一元二次方程的应用,矩形的性质,勾股定理,解题的关键是熟知矩形的判定和性质是解题的关键
(1)根据路程=速度乘以时间列式即可;
(2)四边形为矩形,根据,列方程求解即可;
(3)根据勾股定理,根据,列方程求解即可.
【详解】(1)由题意,得线段,
故答案为:t,;
(2)解:∵四边形为矩形,
则,即,
解得:;
(3)解:过点作于点
在中,根据勾股定理,
已知,
,
则可得方程,
即,
移项可得,
两边同时开平方得;
当时,
移项可得,
解得;
当时,
移项可得,
解得;
所以,经过秒或秒,的长为.
2.如图,在矩形中,,,点从点开始以的速度沿边向移动,点从点开始以的速度沿边向点移动.如果、分别从、同时出发,设移动的时间为t. 求:
(1)当t为多少时,的面积等于?
(2)当t为多少时,是以为斜边的直角三角形?
【答案】(1)不存在某一时刻使得的面积等于
(2)当为秒或6秒时,是以为斜边的直角三角形
【分析】本题考查了三角形的面积公式,勾股定理,一元二次方程的应用,熟练掌握一元二次方程的解法是解题的关键.
(1)根据三角形的面积公式列出方程可得出答案.
(2)用含的代数式分别表示图中各线段,在中,利用勾股定理可求出,同理,在中利用勾股定理也可以求出,联合起来,得到关于的一元二次方程,解即可,然后根据实际意义确定的值.
【详解】(1)解:不存在.
设出发秒时的面积等于.
,
,
,
,
原方程无实数根,
即不存在某一时刻使得的面积等于.
(2)解:,
,,,
是以为斜边的直角三角形,
,即,
整理得,
解之得,,
即当为秒或6秒时,是以为斜边的直角三角形.
3.如图,在中,,动点从点出发,沿向点以的速度匀速运动,另一动点从点出发,沿向点以的速度匀速运动,点同时出发,当有一点到达终点时,另一点也同时停止运动,设运动时间为,那么经过多长时间,的面积为?
【答案】
【分析】本题考查了一元二次方程的应用,根据的面积为列方程求解即可.
【详解】解:由题意,得,
,
,
整理,得
解得,
,则,
,
经过,的面积为.
4.综合与实践
如图1,在矩形中,,动点P,Q分别以的速度从点A,B同时出发,点P沿着运动到点B时停止,点Q沿着运动到点A时停止.设运动时间为.
(1)当点P在上运动时, ________, ________;(用含t的代数式表示)
(2)在(1)的条件下,当时,求t的值;
(3)如图2、图3,点P沿着运动到点B的过程中、当的面积为时,求t的值.
【答案】(1);
(2)1
(3)7
【分析】本题主要考查了列代数式,矩形的性质,一元二次方程的应用,解答本题的关键是熟练运用矩形的性质解决问题.
(1)根据路程等于速度乘以时间得到则;
(2)根据矩形的性质得到,再根据直角三角形面积计算公式建立方程求解即可;
(3)分点P在和点P在上两种情况,根据三角形面积计算公式列出方程求解即可.
【详解】(1)解:由题意得,
∴
故答案为:;
(2)解:∵四边形是矩形,
∴,
∴,
∴,
解得或(舍去);
(3)解:当点P在上运动时,,
∵的面积为,
∴,
解得,
由矩形的性质可得
∴点P运动到点C的时间为秒,
∴此种情况不存在;
当点P在上运动时,,
∵的面积为,
∴,
解得或(舍去);
综上所述,.
5.如图,菱形中, 交于点 O, ,动点 M 从 A 点出发沿方向以匀速直线运动到 C 点,动点 N 从 B 点出发沿方向以匀速直线运动到 D 点.若 M,N 同时出发,设运动时间为 t 秒:
(1)当时, , .(用 t 表示)
(2)当秒时, 的面积为多少?
(3)点 M 到达点 C 后立即原路返回,速度保持不变,直到点 N 到达 D 后同时停止运动,那么在整个移 动过程中,是否存在某一时刻,使得的面积为?若存在,求出运动时间;若不存在,请说 明理由.
【答案】(1)
(2)8
(3)或或
【分析】本题主要考查了菱形的性质,动点问题,一元二次方程的应用,
对于(1),先根据菱形的性质求出,可确定时,两个点的位置,即可得出答案;
对于(2),先分别求出,再根据面积公式求出答案;
对于(3),分,,,四种情况,分别表示,再根据面积等于列出方程,求出解即可.
【详解】(1)∵四边形时菱形,
∴.
根据题意可知,
当时,
点M在上,点N在上,
∴,.
故答案为:,;
(2)当时,,
∴,
∴;
(3)存在,理由如下:
当时,
根据题意得,
∴,
∴,
解得或(舍);
当时,
根据题意得,
∴,
∴,
无解;
当时,
根据题意得,
∴,
∴,
解得或(舍);
当时,
根据题意得,
∴,
∴,
解得或(舍).
所以或或.
题型3 图表信息问题
【例3】.某商店购进800个旅游纪念品,进价为每个50元,第一周以每个80元的价格售出200个,第二周若按每个80元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出10个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品以及清仓处理,以每个40元的价格全部售出,如果这批旅游纪念品共获利9000元.
(1)填表(结果需化简)
时间 第一周 第二周 清仓时
单价(元) 80 40
销售量(件) 200
(2)求第二周每个旅游纪念品的销售价格为多少元?
【答案】(1)填表见解析;(2)第二周每个旅游纪念品的销售价格为70元.
【分析】(1)第二周的单价=第一周的单价-降低的价格,销售量=200+10×降低的单价;清仓时的销售量为:800-第一周的销售量-第二周的销售量;
(2)等量关系为:总售价-总进价=9000.把相关数值代入计算即可.
【详解】解:(1)填表(结果需化简)
时间 第一周 第二周 清仓时
单价(元) 80 80-x 40
销售量(件) 200 200+10x 400-10x
故答案为:80-x,200+10x,400-10x;
(2)80×200+(80-x)(200+10x)+40×(400-10x)-800×50=9000,
x2-20x+100=0,
解得:x1=x2=10,
当x=10时,80-x=70.
答:第二周每个旅游纪念品的销售价格为70元.
【点睛】本题主要考查了列代数式以及一元二次方程的应用,找出相等关系列一元二次方程求解是解题的关键.
针对训练3
1.乌克兰危机发生之后,外交战线按照党中央的部署紧急行动,在战火粉飞中已将5200多名同胞安全从乌克兰撤离,电影《万里归途》正是“外交为民”的真实写照,如表是该影片票房的部分数据,(注:票房是指截止发布日期的所有售票累计收入)
影片《万里归途》的部分统计数据
发布日期 10月8日 10月11日 10月12日
发布次数 第1次 第2次 第3次
票房 10亿元 12.1亿元
(1)平均每次累计票房增长的百分率是多少?
(2)在(1)的条件下,若票价每张40元,求10月11日卖出多少张电影票
【答案】(1)10%
(2)2500000张
【分析】(1)设平均每次累计票房增长的百分率是,利用第3次累计票房=第1次累计票房(1+平均每次累计票房增长的百分率),即可得出关于的一元二次方程,解之取其正值即可得出结论;
(2)利用数量=总结单价,即可求出结论;
【详解】(1)解:设平均每次累计票房增长的百分率是,
依题意得:,
解得:,(不符合题意,舍去).
答:平均每次累计票房增长的百分率是10%.
(2)解:
(张).
答:10月11日卖出2500000张电影票.
(或(张).)
【点睛】本题考查了一元二次方程的应用以及统计表,找准等量关系,正确列出一元二次方程是解题的关键.
2.请阅读下列材料,并按要求完成相应的任务:
人类对一元二次方程的研究经历了漫长的岁月.一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中.到了中世纪,阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法,并用几何法进行了证明.我国古代三国时期的数学家赵爽也给出了类似的几何解法.赵爽在其所著的《勾股圆方图注》中记载了解方程即得方法.首先构造了如图1所示得图形,图中的大正方形面积是,其中四个全等的小矩形面积分别为,中间的小正方形面积为,所以大正方形的面积又可表示为,据此易得.
任务:
(1)参照上述图解一元二次方程的方法,请在下面三个构图中选择能够说明方程的正确构图是 (从序号①②③中选择).
(2)请你通过上述问题的学习,在图2的网格中设计正确的构图,用几何法求解方程(写出必要的思考过程).
【答案】(1)②;(2).
【分析】(1)仿照案例构造图形,即可判断正确构图;
(2)仿照案例构造图形即可求得x的值.
【详解】解:(1)应构造面积是的大正方形,其中四个全等的小矩形面积分别为,中间的小正方形的面积为,所以大正方形的面积又可表示为,进一步可知大正方形的边长为8,所以,得.故正确构图的是②.
故答案为:②;
(2)首先构造了如图2所示的图形.
图中的大正方形面积是,其中四个全等的小矩形面积分别为,中间的小正方形面积为,所以大正方形的面积又可表示为,进一步可知大正方形的边长为8,所以,得.
【点睛】本题是材料阅读题,考查了构造图形解一元二次方程,关键是读懂材料中提供的构图方法,并能正确构图解一元二次方程.体现了数形结合的思想.
3.小王某月手机话费中的各项费用统计情况见下列图所示,其中月功能费为5元,请你根据统计图的信息完成下列各题:
(1)该月小王手机话费共有________元.
(2)扇形统计图中,表示短信费的扇形的圆心角______度.
(3)请将条形统计图补充完整.
(4)电信公司为让利给用户,从下月起每月将对长途话费进行打折优惠,如果小王每月长途电话的通话时间不变,那么两个月后,月长途花费将降至28.8元,那么长途话费的月平均折扣为多少?
【答案】(1)125元;(2)72°;(3)见解析;(4)长途话费的月平均折扣为八折
【分析】(1)根据月功能费在扇形统计图中所占比例计算即可.
(2)用短信费所占比例乘以即可.
(3)用第(1)问中求出的总话费,分别乘以基本话费和长途话费所占比例,求出两者具体金额后填图.
(4)可设长途话费的月平均减少率为,根据题意“两个月后,月长途花费将降至28.8元”可得,解一元二次方程即可.
【详解】(1)元
(2).
(3)如图,
(4)解:设平均减少率为,据题意得
解得
答:长途话费的月平均折扣为八折.
【点睛】本题综合考查了条形统计图与扇形统计图中的数据关系,和一元二次方程解决问题中的增长率问题,熟练掌握相关知识点,找到其中的数量关系并列式计算是解答关键.
4.已知:p为实数.
p k q
… … …
3 16×3+26 2×2×6
4 16×4+26 2×3×7
5 16×5+26 2×4×8
6 16×6+26 2×5×9
7 16×7+26 2×6×10
… … …
根据上表中的规律,回答下列问题:
(1)当p为何值时,k=38
(2)当p为何值时,k与q的值相等?
【答案】(1) p=;(2)当p=8或p=-2时,k=q.
【分析】(1)首先根据表格总结出k、p之间的关系,然后将38代入求得p值即可;
(2)根据表格中有关数字的规律找到q与p之间的关系,与上题中的关系式联立组成有关p的一元二次方程求解即可.
【详解】(1)由题意得:k=16p+26.
当k=38时,38=16p+26,
则p=.
答:当p=时,k=38.
(2)根据题意,得 :q=2(p﹣1)(p+3).
当k=q时,则有16p+26=2(p﹣1)(p+3).
整理,得:p2﹣6p﹣16=0.
解方程,得:p1=8,p2=﹣2.
答:当p=8或p=﹣2时,k=q.
【点睛】本题考查了一元二次方程的应用及数字的变化类问题,解题的关键是通过观察题目中的表格总结出各个未知数之间的关系.
5.某旅行社一则旅游消息如下:
旅游人数 收费标准
不超过人 人均收费元
超过人 每增加一人,人均收费减少元,但人均收费不低于元
(1)甲公司员工分两批参加该项旅游,分别支付给旅行社元和元,甲公司员工有__________人.
(2)乙公司员工一起参加该项旅游,支付给旅行社元,乙公司员工多少人?
【答案】(1)15;
(2)乙公司人.
【分析】(1)设甲公司员工有x人,根据第一次、第二次支付的费用和人均收费标准,判断出两次都不超过10人,直接用总费用除以人均收费,即可得出答案;
(2)设乙公司员工人,根据支付的费用先判断出公司去的人数超过了10人,再根据每增加一人,人均收费减少60元,列出方程,求出的值,再根据人均收费不低于1500元,即可得出乙公司去的人数.
【详解】(1)解:设甲公司有人,
,
,
(人).
故答案为:
(2)设乙公司人,
,
,,
若,每人费用:,不符舍去,
若,每人费用:,符合,
答:乙公司人.
【点睛】此题考查了一元二次方程的应用,读懂题意正确列式和列方程是解题的关键.
能力提升 创新拓展
1.在数学综合与实践课上,李老师让同学们以“正方形折叠”为主题开展数学活动.
【具体操作】如图1,在正方形中,将沿过点的直线翻折,点落在正方形内部的点处,得到,折痕为;再将沿过点的直线翻折,使与重合,得到,折痕为.由以上操作,不难发现,,三点在同一条直线上.
【问题解决】
(1)请直接写出 ;
(2)若,,求正方形的边长;
【深入探究】
(3)如图2,再将沿所在直线折叠,点恰好落在线段的点处,得到,线段与相交于点,请写出,,三条线段的数量关系,并说明理由.
【答案】(1);(2)正方形的边长为6;(3),见解析
【分析】(1)由正方形的性质可得,由折叠的性质可得,,再由计算即可得解;
(2)由折叠可知,,,设正方形边长为,则,,再由勾股定理计算即可得解;
(3)由正方形的性质可得,由折叠的性质可知,,,,证明,得出,从而得出,再求出,由直角三角形的性质可得,即可得解.
【详解】(1)∵四边形为正方形,
∴,
由折叠的性质可得:,,
∴;
(2)由折叠可知,,
所以,
设正方形边长为,则,,
因为在中,,
所以,
整理得,,
解得,或(舍去),
所以正方形的边长为6;
(3),
∵四边形是正方形,
∴,
由折叠的性质可知,,,,
∴,
又∵,
∴,
由(1)得,
∴是等腰直角三角形,
∴,
∴,
∴,
∵,
∴,
由折叠的性质可知,
∵点,,共线,
∴,
∴,
∴在中,,
∴.
【点睛】本题考查了正方形的性质、折叠的性质、勾股定理、全等三角形的判定与性质、直角三角形的性质,熟练掌握以上知识点并灵活运用是解此题的关键.
2.在日历上,我们可以发现其中某些数满足一定的规律,如图是2019年1月份的日历.我们任意选择其中所示的菱形框部分,将每个菱形框部分中去掉中间位置的数之后,相对的两对数分别相乘,再相减,例如:,.不难发现,结果都是48.
(1)请证明发现的规律;
(2)若用一个如图所示菱形框,再框出5个数字,其中最小数与最大数的积为435,求出这5个数中的最大数;
(3)嘉琪说:她用一个如图所示菱形框,框出5个数字,其中最小数与最大数的积是95,直接判断他的说法是否正确(不必叙述理由).
【答案】(1)证明见解析;(2)这5个数中最大数为29.(3)嘉琪的说法不正确.
【分析】(1)、根据题目数据,设中间的数为a,则另外4个数可以用a的式子表示出来,即可列出算式进行证明;
(2)、设最大数为x,列出方程组解答即可;
(3)参考(2)问题思路,解出最大数,然后根据最大数所在位置即可判定.
【详解】(1)证明:设中间的数为a,则另外4个数分别为(a﹣7),(a﹣1),(a+1),(a+7),
∴(a﹣1)(a+1)﹣(a﹣7)(a+7),
=a2﹣1﹣(a2﹣49),
=48.
(2)解:设这5个数中最大数为x,则最小数为(x﹣14),
依题意,得:x(x﹣14)=435,
解得:x1=29,x2=﹣15(不合题意,舍去).
答:设这5个数中最大数为29.
(3)嘉琪的说法不正确.
设这5个数中最大数为y,则最小数为(y﹣14),依题意,得:y(y﹣14)=95,解得:y1=19,y2=﹣5(不合题意,舍去).∵19在日历的最后一列,∴不符合题意,∴嘉琪的说法不正确.
【点睛】本题考查方程的应用问题,解题关键是准确的设未知数,然后列出方程解答.
3.如图,在矩形中,,,点从点出发沿以的速度向点移动;同时,点从点出发沿以的速度向点移动,当其中一点到达终点运动即停止.设运动时间为秒.
(1)在运动过程中,的长度能否为?若能,求出的值,若不能,请说明理由;
(2)在运动过程中,的面积能否为?若能,求出的值,若不能,请说明理由;
(3)取的中点,运动过程中,当时,求的值.
【答案】(1)当时的长度能为,理由见解析
(2)的面积能为,理由见解析
(3),
【分析】(1)由题意可知:,,,根据勾股定理及一元二次方程根的判别式,即可判定;
(2)设运动秒后的面积为,则,,,,利用分割图形求面积法结合的面积为,即可得出关于的一元二次方程,解之即可得出结论;
(3)以为坐标原点,所在直线为轴,建立平面直角坐标系,设,,则,取的中点,连接,则,根据直角三角形的性质可得,再根据两点间的距离公式,可得,解方程即可求得.
【详解】(1)解:的长度能为,理由如下:
根据题意可知:,,,
四边形是矩形,
,
在中,,
,
解得:(舍去)或,
当时的长度能为;
(2)解:不能,理由如下:
设运动秒后的面积为,则,,,,
,
,
,
,
,
即,
,
,
方程无实数根,
的面积不能为;
(3)解:如图,以为坐标原点,所在直线为轴,建立平面直角坐标系,
设,,
的中点为
,
又,,
取的中点,连接,则,
,
,
,
解得:,.
【点睛】本题考查了一元二次方程的应用,勾股定理,矩形的性质,坐标与图形,一元二次方程根的判别式,两点间的距离公式,解答本题的关键是熟练掌握所涉及到的知识点并灵活运用.
典例精讲 1
典例精讲2
典例精讲3
典例精讲 1
典例精讲2
典例精讲3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2025年新九年级数学人教版暑假大讲堂
第七讲 实际问题与一元二次方程(二)
知识点梳理
知识点1 与图形有关的问题
与图形有关的问题通常涉及面积、周长、边长等几何量的计算。这类问题可能需要利用一元二次方程来求解。例如,已知矩形的面积和一边长,求另一边长;或者知道三角形的两边长和第三边的方程,求三角形的周长等。
要点诠释:
面积问题应注意三点:
(1)图形的面积公式是基本的等量关系
(2)利用平移的性质把零散的图形拼接在一起
(3)取舍根时注意图形中边长的限制。
知识点2 动态几何问题
动态几何问题涉及图形在运动或变化过程中的性质。这类问题可能需要通过一元二次方程来描述图形的运动轨迹或变化规律。例如,一个点在一个圆上运动,其到圆心的距离与运动时间的关系可能符合一元二次方程。
要点诠释:
(1)明确动点的运动方向、速度及终止条件(如到达终点停止),将运动过程分段处理。分阶段计算。
(2)注意时间变量的取值范围
知识点3 图形图表信息问题
一元二次方程实际问题中图表信息问题的解题要点主要包括以下几个步骤 :
分析题意,找到题中未知数和题给条件的相等关系 :首先,需要仔细阅读题目,理解题目中的条件和要求,明确需要求解的未知数。然后,找出题目中给出的条件与未知数之间的关系,通常这种关系可以通过等式来表示。
设未知数,并用所设的未知数的代数式表示其余的未知数 :根据找到的相等关系,设定一个或多个未知数。然后,用这些未知数表示题目中给出的其他数值或条件。
找出相等关系,并用它列出方程 :根据设定的未知数和找到的相等关系,列出包含这些未知数的等式。这个等式就是一元二次方程。
解方程求出题中未知数的值 :使用代数方法解这个一元二次方程,求出未知数的值。这一步可能需要使用配方法、公式法等方法。
检验所求的答案是否符合题意 :最后,将求得的答案代入原问题中进行检验,确保答案符合题目的所有条件。
题型1 图形面积问题
【例1】.如图,某校课外生物小组的试验园地是长32米 宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为578平方米,则小道的宽为多少米
针对训练1
1.某园林公司举行盆景展览,如图所示是用这两种盆景摆成的图案,黑色圆点为六月雪盆景,黑色正方形为九里香盆景.图1中六月雪盆景数量为4,九里香盆景数量为2;图2中六月雪盆景数量为6,九里香盆景数量为6;图3中六月雪盆景数量为8,九里香盆景数量为12;…
按照以上规律,解决下列问题:
(1)图5中,六月雪盆景数量为_______,九里香盆景数量为_______;
(2)若园林公司用这两种盆景共132盆按如上规律摆成一个图案,请求出该图案中六月雪和九里香这两种盆景分别多少盆?
2.某社区计划将一个长12米、宽8米的长方形花坛扩建为公共休息区.扩建方案是在花坛四面修建一条宽度相同的小道,使扩建后的长方形公共休息区的总面积为192平方米.
(1)求这条小道的宽度;
(2)如果用篱笆围住扩建后的休息区,需要多少米篱笆?
3.综合与实践.
项目主题:制作新学期的开学手册封面
素材一:小华设计的开学手册的封面是尺寸为长,宽的长方形,正中央有一个长方形边框,其四周是边衬.上下边衬等宽,左右边衬等宽,且上下边衬的宽度是左右边衬宽度的一半.小华设计的边衬面积为172.
素材二:封面边框内需要张贴一张长方形的校园照片.为了使排版规范,照片的长宽比例等于边框的长宽比例.小华设计照片到边框下方的下距为,到边框左右的左距与右距,以及到边框上方的上距都为.
【任务一】设上边衬的宽度为,用含x的代数式表示边框的长和宽.
【任务二】求边框的长和宽.
【任务三】通过计算说明,小华的设计是否规范.
4.根据以下素材,探索完成任务.
探索设计停车场
背景 社区利用一块长方形空地建了一个小型停车场,其布局如图所示,空地四周围墙,需留出通道出行,入口在左上角,出口在右下角.已知,.按照中小车型停车位划线标准,停车位的宽度都相同,且停车位的宽度不小于.
方案 如图,设计四列阴影部分为停车位,且停车位的宽度相同,即,其余部分是等宽的通道.
任务1 若停车位总面积为,请计算停车位的宽度是否符合标准.
任务2 若通道的宽度要求不小于,当停车位宽度取多少时,停车位总面积最大,并求出最大停车位总面积.
5.综合实践——用矩形硬纸片制作无盖纸盒.
如图1,有一张长,宽的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图2所示的无盖纸盒.(硬纸片厚度忽略不计)
(1)若纸盒的底面积为,请计算剪去的正方形的边长;
(2)如图3,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒.若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
题型2 动态几何问题
【例2】.如图,在中,,,,动点 P从点 A 出发沿边向点B以的速度移动,同时动点Q从点 B 出发沿边向点 C 以的速度移动,当 P 运动到 B 点时 P、Q 两点同时停止运动,设运动时间为.
(1) ; ;(用t的代数式表示)
(2)D是的中点,连接、,t为何值时的面积为?
针对训练2
1.如图所示,在四边形中,,,,动点从点出发沿AD方向向点以的速度运动,动点从点开始沿着方向向点以的速度运动.点分别从点和点同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)当运动秒时,线段__________(用含有t的代数式表示)
(2)经过多长时间,四边形是矩形?
(3)经过多长时间,PQ的长为?
2.如图,在矩形中,,,点从点开始以的速度沿边向移动,点从点开始以的速度沿边向点移动.如果、分别从、同时出发,设移动的时间为t. 求:
(1)当t为多少时,的面积等于?
(2)当t为多少时,是以为斜边的直角三角形?
3.如图,在中,,动点从点出发,沿向点以的速度匀速运动,另一动点从点出发,沿向点以的速度匀速运动,点同时出发,当有一点到达终点时,另一点也同时停止运动,设运动时间为,那么经过多长时间,的面积为?
4.综合与实践
如图1,在矩形中,,动点P,Q分别以的速度从点A,B同时出发,点P沿着运动到点B时停止,点Q沿着运动到点A时停止.设运动时间为.
(1)当点P在上运动时, ________, ________;(用含t的代数式表示)
(2)在(1)的条件下,当时,求t的值;
(3)如图2、图3,点P沿着运动到点B的过程中、当的面积为时,求t的值.
5.如图,菱形中, 交于点 O, ,动点 M 从 A 点出发沿方向以匀速直线运动到 C 点,动点 N 从 B 点出发沿方向以匀速直线运动到 D 点.若 M,N 同时出发,设运动时间为 t 秒:
(1)当时, , .(用 t 表示)
(2)当秒时, 的面积为多少?
(3)点 M 到达点 C 后立即原路返回,速度保持不变,直到点 N 到达 D 后同时停止运动,那么在整个移 动过程中,是否存在某一时刻,使得的面积为?若存在,求出运动时间;若不存在,请说 明理由.
题型3 图表信息问题
【例3】.某商店购进800个旅游纪念品,进价为每个50元,第一周以每个80元的价格售出200个,第二周若按每个80元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出10个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品以及清仓处理,以每个40元的价格全部售出,如果这批旅游纪念品共获利9000元.
(1)填表(结果需化简)
时间 第一周 第二周 清仓时
单价(元) 80 40
销售量(件) 200
(2)求第二周每个旅游纪念品的销售价格为多少元?
针对训练3
1.乌克兰危机发生之后,外交战线按照党中央的部署紧急行动,在战火粉飞中已将5200多名同胞安全从乌克兰撤离,电影《万里归途》正是“外交为民”的真实写照,如表是该影片票房的部分数据,(注:票房是指截止发布日期的所有售票累计收入)
影片《万里归途》的部分统计数据
发布日期 10月8日 10月11日 10月12日
发布次数 第1次 第2次 第3次
票房 10亿元 12.1亿元
(1)平均每次累计票房增长的百分率是多少?
(2)在(1)的条件下,若票价每张40元,求10月11日卖出多少张电影票
2.请阅读下列材料,并按要求完成相应的任务:
人类对一元二次方程的研究经历了漫长的岁月.一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中.到了中世纪,阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法,并用几何法进行了证明.我国古代三国时期的数学家赵爽也给出了类似的几何解法.赵爽在其所著的《勾股圆方图注》中记载了解方程即得方法.首先构造了如图1所示得图形,图中的大正方形面积是,其中四个全等的小矩形面积分别为,中间的小正方形面积为,所以大正方形的面积又可表示为,据此易得.
任务:
(1)参照上述图解一元二次方程的方法,请在下面三个构图中选择能够说明方程的正确构图是 (从序号①②③中选择).
(2)请你通过上述问题的学习,在图2的网格中设计正确的构图,用几何法求解方程(写出必要的思考过程).
3.小王某月手机话费中的各项费用统计情况见下列图所示,其中月功能费为5元,请你根据统计图的信息完成下列各题:
(1)该月小王手机话费共有________元.
(2)扇形统计图中,表示短信费的扇形的圆心角______度.
(3)请将条形统计图补充完整.
(4)电信公司为让利给用户,从下月起每月将对长途话费进行打折优惠,如果小王每月长途电话的通话时间不变,那么两个月后,月长途花费将降至28.8元,那么长途话费的月平均折扣为多少?
4.已知:p为实数.
p k q
… … …
3 16×3+26 2×2×6
4 16×4+26 2×3×7
5 16×5+26 2×4×8
6 16×6+26 2×5×9
7 16×7+26 2×6×10
… … …
根据上表中的规律,回答下列问题:
(1)当p为何值时,k=38
(2)当p为何值时,k与q的值相等?
5.某旅行社一则旅游消息如下:
旅游人数 收费标准
不超过人 人均收费元
超过人 每增加一人,人均收费减少元,但人均收费不低于元
(1)甲公司员工分两批参加该项旅游,分别支付给旅行社元和元,甲公司员工有__________人.
(2)乙公司员工一起参加该项旅游,支付给旅行社元,乙公司员工多少人?
能力提升 创新拓展
1.在数学综合与实践课上,李老师让同学们以“正方形折叠”为主题开展数学活动.
【具体操作】如图1,在正方形中,将沿过点的直线翻折,点落在正方形内部的点处,得到,折痕为;再将沿过点的直线翻折,使与重合,得到,折痕为.由以上操作,不难发现,,三点在同一条直线上.
【问题解决】
(1)请直接写出 ;
(2)若,,求正方形的边长;
【深入探究】
(3)如图2,再将沿所在直线折叠,点恰好落在线段的点处,得到,线段与相交于点,请写出,,三条线段的数量关系,并说明理由.
2.在日历上,我们可以发现其中某些数满足一定的规律,如图是2019年1月份的日历.我们任意选择其中所示的菱形框部分,将每个菱形框部分中去掉中间位置的数之后,相对的两对数分别相乘,再相减,例如:,.不难发现,结果都是48.
(1)请证明发现的规律;
(2)若用一个如图所示菱形框,再框出5个数字,其中最小数与最大数的积为435,求出这5个数中的最大数;
(3)嘉琪说:她用一个如图所示菱形框,框出5个数字,其中最小数与最大数的积是95,直接判断他的说法是否正确(不必叙述理由).
3.如图,在矩形中,,,点从点出发沿以的速度向点移动;同时,点从点出发沿以的速度向点移动,当其中一点到达终点运动即停止.设运动时间为秒.
(1)在运动过程中,的长度能否为?若能,求出的值,若不能,请说明理由;
(2)在运动过程中,的面积能否为?若能,求出的值,若不能,请说明理由;
(3)取的中点,运动过程中,当时,求的值.
2025年新九年级数学人教版暑假大讲堂
第七讲 实际问题与一元二次方程(二)(解析版)
知识点梳理
知识点1 与图形有关的问题
与图形有关的问题通常涉及面积、周长、边长等几何量的计算。这类问题可能需要利用一元二次方程来求解。例如,已知矩形的面积和一边长,求另一边长;或者知道三角形的两边长和第三边的方程,求三角形的周长等。
要点诠释:
面积问题应注意三点:
(1)图形的面积公式是基本的等量关系
(2)利用平移的性质把零散的图形拼接在一起
(3)取舍根时注意图形中边长的限制。
知识点2 动态几何问题
动态几何问题涉及图形在运动或变化过程中的性质。这类问题可能需要通过一元二次方程来描述图形的运动轨迹或变化规律。例如,一个点在一个圆上运动,其到圆心的距离与运动时间的关系可能符合一元二次方程。
要点诠释:
(1)明确动点的运动方向、速度及终止条件(如到达终点停止),将运动过程分段处理。分阶段计算。
(2)注意时间变量的取值范围
知识点3 图形图表信息问题
一元二次方程实际问题中图表信息问题的解题要点主要包括以下几个步骤 :
分析题意,找到题中未知数和题给条件的相等关系 :首先,需要仔细阅读题目,理解题目中的条件和要求,明确需要求解的未知数。然后,找出题目中给出的条件与未知数之间的关系,通常这种关系可以通过等式来表示。
设未知数,并用所设的未知数的代数式表示其余的未知数 :根据找到的相等关系,设定一个或多个未知数。然后,用这些未知数表示题目中给出的其他数值或条件。
找出相等关系,并用它列出方程 :根据设定的未知数和找到的相等关系,列出包含这些未知数的等式。这个等式就是一元二次方程。
解方程求出题中未知数的值 :使用代数方法解这个一元二次方程,求出未知数的值。这一步可能需要使用配方法、公式法等方法。
检验所求的答案是否符合题意 :最后,将求得的答案代入原问题中进行检验,确保答案符合题目的所有条件。
题型1 图形面积问题
【例1】.如图,某校课外生物小组的试验园地是长32米 宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为578平方米,则小道的宽为多少米
【答案】米.
【分析】本题考查了一元二次方程的应用面积问题,解题的关键是巧妙的运用等积代换.
设小道的宽为米,则长、宽分别为米、米,根据矩形的面积公式就可以列出方程,解方程即可.
【详解】解:设该小道的宽为米,依题意得
,
解得,.
因为,不合题意,舍去.
所以.
答:小道宽米.
针对训练1
1.某园林公司举行盆景展览,如图所示是用这两种盆景摆成的图案,黑色圆点为六月雪盆景,黑色正方形为九里香盆景.图1中六月雪盆景数量为4,九里香盆景数量为2;图2中六月雪盆景数量为6,九里香盆景数量为6;图3中六月雪盆景数量为8,九里香盆景数量为12;…
按照以上规律,解决下列问题:
(1)图5中,六月雪盆景数量为_______,九里香盆景数量为_______;
(2)若园林公司用这两种盆景共132盆按如上规律摆成一个图案,请求出该图案中六月雪和九里香这两种盆景分别多少盆?
【答案】(1)12;30
(2)六月雪盆景有22盆,九里香盆景有110盆
【分析】本题考查了图形规律探索、一元二次方程的应用,观察图形的变化找到隐含的规律是解题的关键.
(1)观察图形,得出第个图中六月雪盆景数量为,九里香盆景数量为,再代入即可求解;
(2)设该图案为如上规律的第个图,根据题意列出方程,解出的值,即可解答.
【详解】(1)解:图1中六月雪盆景数量为,九里香盆景数量为,
图2中六月雪盆景数量为,九里香盆景数量为,
图3中六月雪盆景数量为,九里香盆景数量为,
图4中六月雪盆景数量为,九里香盆景数量为,
…
第个图中六月雪盆景数量为,九里香盆景数量为,
当时,,,
图5中,六月雪盆景数量为12,九里香盆景数量为30.
故答案为:12;30.
(2)解:设该图案为如上规律的第个图,
由题意得,,
解得:,(不符合题意,舍去),
此时六月雪盆景数量为盆,九里香盆景数量为盆,
答:六月雪盆景有22盆,九里香盆景有110盆.
2.某社区计划将一个长12米、宽8米的长方形花坛扩建为公共休息区.扩建方案是在花坛四面修建一条宽度相同的小道,使扩建后的长方形公共休息区的总面积为192平方米.
(1)求这条小道的宽度;
(2)如果用篱笆围住扩建后的休息区,需要多少米篱笆?
【答案】(1)这条小道的宽度为2米
(2)需要56米篱笆
【分析】本题考查了一元二次方程的应用,找准等量关系,正确建立方程是解题关键.
(1)设这条小道的宽度为米,根据扩建后的长方形公共休息区的总面积为192平方米建立方程,解方程即可得;
(2)根据(1)的结果求出扩建后的长方形公共休息区的长与宽,再利用长方形的周长公式计算即可得.
【详解】(1)解:设这条小道的宽度为米,
由题意得:,
解得或(不符合题意,舍去),
答:这条小道的宽度为2米.
(2)解:由(1)可知,扩建后的长方形公共休息区的长为(米),宽为(米),
则(米),
答:如果用篱笆围住扩建后的休息区,需要56米篱笆.
3.综合与实践.
项目主题:制作新学期的开学手册封面
素材一:小华设计的开学手册的封面是尺寸为长,宽的长方形,正中央有一个长方形边框,其四周是边衬.上下边衬等宽,左右边衬等宽,且上下边衬的宽度是左右边衬宽度的一半.小华设计的边衬面积为172.
素材二:封面边框内需要张贴一张长方形的校园照片.为了使排版规范,照片的长宽比例等于边框的长宽比例.小华设计照片到边框下方的下距为,到边框左右的左距与右距,以及到边框上方的上距都为.
【任务一】设上边衬的宽度为,用含x的代数式表示边框的长和宽.
【任务二】求边框的长和宽.
【任务三】通过计算说明,小华的设计是否规范.
【答案】任务一:边框的长和宽为,;任务二:长和宽为与;任务三:设计符合规范,见解析
【分析】本题考查了一元二次方程的应用、列代数式以及有理数的混合运算,解题的关键是:根据各边之间的关系,用含的代数式表示出边框的长和宽;找准等量关系,正确列出一元二次方程;验证照片的长宽比例是否等于边框的长宽比例.
[任务一]设上边衬的宽度为,则下边衬的宽度为,左、右边衬的宽度为,利用边框的长上边衬的宽度下边衬的宽度及边框的宽左边衬的宽度又边衬的宽度,即可用含的代数式表示出边框的长和宽;
[任务二]根据小华设计的边衬面积为,可列出关于的一元二次方程,解之可得出的值,再将其符合题意的值代入及中,即可求出结论;
[任务三]求出照片的长、宽,结合照片的长宽比例等于边框的长宽比例,即可得出结论.
【详解】解:[任务一]设上边衬的宽度为,则下边衬的宽度为,左、右边衬的宽度为,
边框的长为,宽为;
[任务二]根据题意得:,
整理得:,
解得:,(不符合题意,舍去),
,
.
答:边框的长为,宽为;
[任务三]小华的设计规范,理由如下:
照片的长为,
照片的宽为,
边框的长为,宽为,且,
小华的设计规范.
4.根据以下素材,探索完成任务.
探索设计停车场
背景 社区利用一块长方形空地建了一个小型停车场,其布局如图所示,空地四周围墙,需留出通道出行,入口在左上角,出口在右下角.已知,.按照中小车型停车位划线标准,停车位的宽度都相同,且停车位的宽度不小于.
方案 如图,设计四列阴影部分为停车位,且停车位的宽度相同,即,其余部分是等宽的通道.
任务1 若停车位总面积为,请计算停车位的宽度是否符合标准.
任务2 若通道的宽度要求不小于,当停车位宽度取多少时,停车位总面积最大,并求出最大停车位总面积.
【答案】任务1:停车位的宽度符合标准;任务2:当停车位的宽度为时,停车位的总面积最大为
【分析】本题考查一元二次方程的实际应用,配方法的应用,读懂题意,正确的列出方程,是解题的关键:
任务1:设停车位的宽度为,通道的宽度为,根据图形可知:,进而得到,根据停车位总面积为,列出方程进行求解后,结合停车位的宽度不小于进行判断即可;
任务2:设停车位的总面积为,面积公式表示出,配方法求最值即可.
【详解】解:任务1:设停车位的宽度为,通道的宽度为,由图和题意可知:,
∴,
∵停车位总面积为,
∴,
把代入,得:,
解得:或(舍去);
∵,
∴停车位的宽度符合标准.
任务2:设停车位的总面积为,由任务1可知:,
∴
,
,
∵且,
∴,
∴当时,最大,
答:当停车位的宽度为时,停车位的总面积最大为.
5.综合实践——用矩形硬纸片制作无盖纸盒.
如图1,有一张长,宽的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图2所示的无盖纸盒.(硬纸片厚度忽略不计)
(1)若纸盒的底面积为,请计算剪去的正方形的边长;
(2)如图3,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒.若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
【答案】(1)
(2)
【分析】本题考查了一元二次方程的应用,理解题意,正确列出一元二次方程是解此题的关键.
(1)设减去的正方形的边长为,则纸盒底面长方形的长为,宽为,根据题意列出一元二次方程,解方程即可得出答案;
(2)设剪去的正方形的边长为,根据题意列出一元二次方程,解方程即可得出答案.
【详解】(1)解:设减去的正方形的边长为,则纸盒底面长方形的长为,宽为,
由题意得:,
解得:或(舍去),
∴剪去正方形的边长为;
(2)解:设剪去的正方形的边长为,
由题意得:,
解得:或(不符合题意,舍去),
∴剪去的正方形的边长为.
题型2 动态几何问题
【例2】.如图,在中,,,,动点 P从点 A 出发沿边向点B以的速度移动,同时动点Q从点 B 出发沿边向点 C 以的速度移动,当 P 运动到 B 点时 P、Q 两点同时停止运动,设运动时间为.
(1) ; ;(用t的代数式表示)
(2)D是的中点,连接、,t为何值时的面积为?
【答案】(1),
(2)或4
【分析】本题主要考查了一元二次方程的应用,解题的关键是读懂题意,找到关键描述语,列出等量关系.
(1)根据速度时间路程,列出代数式即可;
(2)过点D作于H,利用三角形中位线定理求得的长度;然后根据题意和三角形的面积列出方程,求出方程的解即可.
【详解】(1)根据题意得: ,,
,
故答案为:,.
(2)如图,过点D作于H,
∵,即,
∴,
又∵D是的中点,
∴,是的中位线,
∴,
根据题意,得,
整理,得,
解得:,,
当或4时,的面积是.
针对训练2
1.如图所示,在四边形中,,,,动点从点出发沿AD方向向点以的速度运动,动点从点开始沿着方向向点以的速度运动.点分别从点和点同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)当运动秒时,线段__________(用含有t的代数式表示)
(2)经过多长时间,四边形是矩形?
(3)经过多长时间,PQ的长为?
【答案】(1)t,
(2)
(3)经过5秒或9秒,的长为
【分析】此题主要考查一元二次方程的应用,矩形的性质,勾股定理,解题的关键是熟知矩形的判定和性质是解题的关键
(1)根据路程=速度乘以时间列式即可;
(2)四边形为矩形,根据,列方程求解即可;
(3)根据勾股定理,根据,列方程求解即可.
【详解】(1)由题意,得线段,
故答案为:t,;
(2)解:∵四边形为矩形,
则,即,
解得:;
(3)解:过点作于点
在中,根据勾股定理,
已知,
,
则可得方程,
即,
移项可得,
两边同时开平方得;
当时,
移项可得,
解得;
当时,
移项可得,
解得;
所以,经过秒或秒,的长为.
2.如图,在矩形中,,,点从点开始以的速度沿边向移动,点从点开始以的速度沿边向点移动.如果、分别从、同时出发,设移动的时间为t. 求:
(1)当t为多少时,的面积等于?
(2)当t为多少时,是以为斜边的直角三角形?
【答案】(1)不存在某一时刻使得的面积等于
(2)当为秒或6秒时,是以为斜边的直角三角形
【分析】本题考查了三角形的面积公式,勾股定理,一元二次方程的应用,熟练掌握一元二次方程的解法是解题的关键.
(1)根据三角形的面积公式列出方程可得出答案.
(2)用含的代数式分别表示图中各线段,在中,利用勾股定理可求出,同理,在中利用勾股定理也可以求出,联合起来,得到关于的一元二次方程,解即可,然后根据实际意义确定的值.
【详解】(1)解:不存在.
设出发秒时的面积等于.
,
,
,
,
原方程无实数根,
即不存在某一时刻使得的面积等于.
(2)解:,
,,,
是以为斜边的直角三角形,
,即,
整理得,
解之得,,
即当为秒或6秒时,是以为斜边的直角三角形.
3.如图,在中,,动点从点出发,沿向点以的速度匀速运动,另一动点从点出发,沿向点以的速度匀速运动,点同时出发,当有一点到达终点时,另一点也同时停止运动,设运动时间为,那么经过多长时间,的面积为?
【答案】
【分析】本题考查了一元二次方程的应用,根据的面积为列方程求解即可.
【详解】解:由题意,得,
,
,
整理,得
解得,
,则,
,
经过,的面积为.
4.综合与实践
如图1,在矩形中,,动点P,Q分别以的速度从点A,B同时出发,点P沿着运动到点B时停止,点Q沿着运动到点A时停止.设运动时间为.
(1)当点P在上运动时, ________, ________;(用含t的代数式表示)
(2)在(1)的条件下,当时,求t的值;
(3)如图2、图3,点P沿着运动到点B的过程中、当的面积为时,求t的值.
【答案】(1);
(2)1
(3)7
【分析】本题主要考查了列代数式,矩形的性质,一元二次方程的应用,解答本题的关键是熟练运用矩形的性质解决问题.
(1)根据路程等于速度乘以时间得到则;
(2)根据矩形的性质得到,再根据直角三角形面积计算公式建立方程求解即可;
(3)分点P在和点P在上两种情况,根据三角形面积计算公式列出方程求解即可.
【详解】(1)解:由题意得,
∴
故答案为:;
(2)解:∵四边形是矩形,
∴,
∴,
∴,
解得或(舍去);
(3)解:当点P在上运动时,,
∵的面积为,
∴,
解得,
由矩形的性质可得
∴点P运动到点C的时间为秒,
∴此种情况不存在;
当点P在上运动时,,
∵的面积为,
∴,
解得或(舍去);
综上所述,.
5.如图,菱形中, 交于点 O, ,动点 M 从 A 点出发沿方向以匀速直线运动到 C 点,动点 N 从 B 点出发沿方向以匀速直线运动到 D 点.若 M,N 同时出发,设运动时间为 t 秒:
(1)当时, , .(用 t 表示)
(2)当秒时, 的面积为多少?
(3)点 M 到达点 C 后立即原路返回,速度保持不变,直到点 N 到达 D 后同时停止运动,那么在整个移 动过程中,是否存在某一时刻,使得的面积为?若存在,求出运动时间;若不存在,请说 明理由.
【答案】(1)
(2)8
(3)或或
【分析】本题主要考查了菱形的性质,动点问题,一元二次方程的应用,
对于(1),先根据菱形的性质求出,可确定时,两个点的位置,即可得出答案;
对于(2),先分别求出,再根据面积公式求出答案;
对于(3),分,,,四种情况,分别表示,再根据面积等于列出方程,求出解即可.
【详解】(1)∵四边形时菱形,
∴.
根据题意可知,
当时,
点M在上,点N在上,
∴,.
故答案为:,;
(2)当时,,
∴,
∴;
(3)存在,理由如下:
当时,
根据题意得,
∴,
∴,
解得或(舍);
当时,
根据题意得,
∴,
∴,
无解;
当时,
根据题意得,
∴,
∴,
解得或(舍);
当时,
根据题意得,
∴,
∴,
解得或(舍).
所以或或.
题型3 图表信息问题
【例3】.某商店购进800个旅游纪念品,进价为每个50元,第一周以每个80元的价格售出200个,第二周若按每个80元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出10个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品以及清仓处理,以每个40元的价格全部售出,如果这批旅游纪念品共获利9000元.
(1)填表(结果需化简)
时间 第一周 第二周 清仓时
单价(元) 80 40
销售量(件) 200
(2)求第二周每个旅游纪念品的销售价格为多少元?
【答案】(1)填表见解析;(2)第二周每个旅游纪念品的销售价格为70元.
【分析】(1)第二周的单价=第一周的单价-降低的价格,销售量=200+10×降低的单价;清仓时的销售量为:800-第一周的销售量-第二周的销售量;
(2)等量关系为:总售价-总进价=9000.把相关数值代入计算即可.
【详解】解:(1)填表(结果需化简)
时间 第一周 第二周 清仓时
单价(元) 80 80-x 40
销售量(件) 200 200+10x 400-10x
故答案为:80-x,200+10x,400-10x;
(2)80×200+(80-x)(200+10x)+40×(400-10x)-800×50=9000,
x2-20x+100=0,
解得:x1=x2=10,
当x=10时,80-x=70.
答:第二周每个旅游纪念品的销售价格为70元.
【点睛】本题主要考查了列代数式以及一元二次方程的应用,找出相等关系列一元二次方程求解是解题的关键.
针对训练3
1.乌克兰危机发生之后,外交战线按照党中央的部署紧急行动,在战火粉飞中已将5200多名同胞安全从乌克兰撤离,电影《万里归途》正是“外交为民”的真实写照,如表是该影片票房的部分数据,(注:票房是指截止发布日期的所有售票累计收入)
影片《万里归途》的部分统计数据
发布日期 10月8日 10月11日 10月12日
发布次数 第1次 第2次 第3次
票房 10亿元 12.1亿元
(1)平均每次累计票房增长的百分率是多少?
(2)在(1)的条件下,若票价每张40元,求10月11日卖出多少张电影票
【答案】(1)10%
(2)2500000张
【分析】(1)设平均每次累计票房增长的百分率是,利用第3次累计票房=第1次累计票房(1+平均每次累计票房增长的百分率),即可得出关于的一元二次方程,解之取其正值即可得出结论;
(2)利用数量=总结单价,即可求出结论;
【详解】(1)解:设平均每次累计票房增长的百分率是,
依题意得:,
解得:,(不符合题意,舍去).
答:平均每次累计票房增长的百分率是10%.
(2)解:
(张).
答:10月11日卖出2500000张电影票.
(或(张).)
【点睛】本题考查了一元二次方程的应用以及统计表,找准等量关系,正确列出一元二次方程是解题的关键.
2.请阅读下列材料,并按要求完成相应的任务:
人类对一元二次方程的研究经历了漫长的岁月.一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中.到了中世纪,阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法,并用几何法进行了证明.我国古代三国时期的数学家赵爽也给出了类似的几何解法.赵爽在其所著的《勾股圆方图注》中记载了解方程即得方法.首先构造了如图1所示得图形,图中的大正方形面积是,其中四个全等的小矩形面积分别为,中间的小正方形面积为,所以大正方形的面积又可表示为,据此易得.
任务:
(1)参照上述图解一元二次方程的方法,请在下面三个构图中选择能够说明方程的正确构图是 (从序号①②③中选择).
(2)请你通过上述问题的学习,在图2的网格中设计正确的构图,用几何法求解方程(写出必要的思考过程).
【答案】(1)②;(2).
【分析】(1)仿照案例构造图形,即可判断正确构图;
(2)仿照案例构造图形即可求得x的值.
【详解】解:(1)应构造面积是的大正方形,其中四个全等的小矩形面积分别为,中间的小正方形的面积为,所以大正方形的面积又可表示为,进一步可知大正方形的边长为8,所以,得.故正确构图的是②.
故答案为:②;
(2)首先构造了如图2所示的图形.
图中的大正方形面积是,其中四个全等的小矩形面积分别为,中间的小正方形面积为,所以大正方形的面积又可表示为,进一步可知大正方形的边长为8,所以,得.
【点睛】本题是材料阅读题,考查了构造图形解一元二次方程,关键是读懂材料中提供的构图方法,并能正确构图解一元二次方程.体现了数形结合的思想.
3.小王某月手机话费中的各项费用统计情况见下列图所示,其中月功能费为5元,请你根据统计图的信息完成下列各题:
(1)该月小王手机话费共有________元.
(2)扇形统计图中,表示短信费的扇形的圆心角______度.
(3)请将条形统计图补充完整.
(4)电信公司为让利给用户,从下月起每月将对长途话费进行打折优惠,如果小王每月长途电话的通话时间不变,那么两个月后,月长途花费将降至28.8元,那么长途话费的月平均折扣为多少?
【答案】(1)125元;(2)72°;(3)见解析;(4)长途话费的月平均折扣为八折
【分析】(1)根据月功能费在扇形统计图中所占比例计算即可.
(2)用短信费所占比例乘以即可.
(3)用第(1)问中求出的总话费,分别乘以基本话费和长途话费所占比例,求出两者具体金额后填图.
(4)可设长途话费的月平均减少率为,根据题意“两个月后,月长途花费将降至28.8元”可得,解一元二次方程即可.
【详解】(1)元
(2).
(3)如图,
(4)解:设平均减少率为,据题意得
解得
答:长途话费的月平均折扣为八折.
【点睛】本题综合考查了条形统计图与扇形统计图中的数据关系,和一元二次方程解决问题中的增长率问题,熟练掌握相关知识点,找到其中的数量关系并列式计算是解答关键.
4.已知:p为实数.
p k q
… … …
3 16×3+26 2×2×6
4 16×4+26 2×3×7
5 16×5+26 2×4×8
6 16×6+26 2×5×9
7 16×7+26 2×6×10
… … …
根据上表中的规律,回答下列问题:
(1)当p为何值时,k=38
(2)当p为何值时,k与q的值相等?
【答案】(1) p=;(2)当p=8或p=-2时,k=q.
【分析】(1)首先根据表格总结出k、p之间的关系,然后将38代入求得p值即可;
(2)根据表格中有关数字的规律找到q与p之间的关系,与上题中的关系式联立组成有关p的一元二次方程求解即可.
【详解】(1)由题意得:k=16p+26.
当k=38时,38=16p+26,
则p=.
答:当p=时,k=38.
(2)根据题意,得 :q=2(p﹣1)(p+3).
当k=q时,则有16p+26=2(p﹣1)(p+3).
整理,得:p2﹣6p﹣16=0.
解方程,得:p1=8,p2=﹣2.
答:当p=8或p=﹣2时,k=q.
【点睛】本题考查了一元二次方程的应用及数字的变化类问题,解题的关键是通过观察题目中的表格总结出各个未知数之间的关系.
5.某旅行社一则旅游消息如下:
旅游人数 收费标准
不超过人 人均收费元
超过人 每增加一人,人均收费减少元,但人均收费不低于元
(1)甲公司员工分两批参加该项旅游,分别支付给旅行社元和元,甲公司员工有__________人.
(2)乙公司员工一起参加该项旅游,支付给旅行社元,乙公司员工多少人?
【答案】(1)15;
(2)乙公司人.
【分析】(1)设甲公司员工有x人,根据第一次、第二次支付的费用和人均收费标准,判断出两次都不超过10人,直接用总费用除以人均收费,即可得出答案;
(2)设乙公司员工人,根据支付的费用先判断出公司去的人数超过了10人,再根据每增加一人,人均收费减少60元,列出方程,求出的值,再根据人均收费不低于1500元,即可得出乙公司去的人数.
【详解】(1)解:设甲公司有人,
,
,
(人).
故答案为:
(2)设乙公司人,
,
,,
若,每人费用:,不符舍去,
若,每人费用:,符合,
答:乙公司人.
【点睛】此题考查了一元二次方程的应用,读懂题意正确列式和列方程是解题的关键.
能力提升 创新拓展
1.在数学综合与实践课上,李老师让同学们以“正方形折叠”为主题开展数学活动.
【具体操作】如图1,在正方形中,将沿过点的直线翻折,点落在正方形内部的点处,得到,折痕为;再将沿过点的直线翻折,使与重合,得到,折痕为.由以上操作,不难发现,,三点在同一条直线上.
【问题解决】
(1)请直接写出 ;
(2)若,,求正方形的边长;
【深入探究】
(3)如图2,再将沿所在直线折叠,点恰好落在线段的点处,得到,线段与相交于点,请写出,,三条线段的数量关系,并说明理由.
【答案】(1);(2)正方形的边长为6;(3),见解析
【分析】(1)由正方形的性质可得,由折叠的性质可得,,再由计算即可得解;
(2)由折叠可知,,,设正方形边长为,则,,再由勾股定理计算即可得解;
(3)由正方形的性质可得,由折叠的性质可知,,,,证明,得出,从而得出,再求出,由直角三角形的性质可得,即可得解.
【详解】(1)∵四边形为正方形,
∴,
由折叠的性质可得:,,
∴;
(2)由折叠可知,,
所以,
设正方形边长为,则,,
因为在中,,
所以,
整理得,,
解得,或(舍去),
所以正方形的边长为6;
(3),
∵四边形是正方形,
∴,
由折叠的性质可知,,,,
∴,
又∵,
∴,
由(1)得,
∴是等腰直角三角形,
∴,
∴,
∴,
∵,
∴,
由折叠的性质可知,
∵点,,共线,
∴,
∴,
∴在中,,
∴.
【点睛】本题考查了正方形的性质、折叠的性质、勾股定理、全等三角形的判定与性质、直角三角形的性质,熟练掌握以上知识点并灵活运用是解此题的关键.
2.在日历上,我们可以发现其中某些数满足一定的规律,如图是2019年1月份的日历.我们任意选择其中所示的菱形框部分,将每个菱形框部分中去掉中间位置的数之后,相对的两对数分别相乘,再相减,例如:,.不难发现,结果都是48.
(1)请证明发现的规律;
(2)若用一个如图所示菱形框,再框出5个数字,其中最小数与最大数的积为435,求出这5个数中的最大数;
(3)嘉琪说:她用一个如图所示菱形框,框出5个数字,其中最小数与最大数的积是95,直接判断他的说法是否正确(不必叙述理由).
【答案】(1)证明见解析;(2)这5个数中最大数为29.(3)嘉琪的说法不正确.
【分析】(1)、根据题目数据,设中间的数为a,则另外4个数可以用a的式子表示出来,即可列出算式进行证明;
(2)、设最大数为x,列出方程组解答即可;
(3)参考(2)问题思路,解出最大数,然后根据最大数所在位置即可判定.
【详解】(1)证明:设中间的数为a,则另外4个数分别为(a﹣7),(a﹣1),(a+1),(a+7),
∴(a﹣1)(a+1)﹣(a﹣7)(a+7),
=a2﹣1﹣(a2﹣49),
=48.
(2)解:设这5个数中最大数为x,则最小数为(x﹣14),
依题意,得:x(x﹣14)=435,
解得:x1=29,x2=﹣15(不合题意,舍去).
答:设这5个数中最大数为29.
(3)嘉琪的说法不正确.
设这5个数中最大数为y,则最小数为(y﹣14),依题意,得:y(y﹣14)=95,解得:y1=19,y2=﹣5(不合题意,舍去).∵19在日历的最后一列,∴不符合题意,∴嘉琪的说法不正确.
【点睛】本题考查方程的应用问题,解题关键是准确的设未知数,然后列出方程解答.
3.如图,在矩形中,,,点从点出发沿以的速度向点移动;同时,点从点出发沿以的速度向点移动,当其中一点到达终点运动即停止.设运动时间为秒.
(1)在运动过程中,的长度能否为?若能,求出的值,若不能,请说明理由;
(2)在运动过程中,的面积能否为?若能,求出的值,若不能,请说明理由;
(3)取的中点,运动过程中,当时,求的值.
【答案】(1)当时的长度能为,理由见解析
(2)的面积能为,理由见解析
(3),
【分析】(1)由题意可知:,,,根据勾股定理及一元二次方程根的判别式,即可判定;
(2)设运动秒后的面积为,则,,,,利用分割图形求面积法结合的面积为,即可得出关于的一元二次方程,解之即可得出结论;
(3)以为坐标原点,所在直线为轴,建立平面直角坐标系,设,,则,取的中点,连接,则,根据直角三角形的性质可得,再根据两点间的距离公式,可得,解方程即可求得.
【详解】(1)解:的长度能为,理由如下:
根据题意可知:,,,
四边形是矩形,
,
在中,,
,
解得:(舍去)或,
当时的长度能为;
(2)解:不能,理由如下:
设运动秒后的面积为,则,,,,
,
,
,
,
,
即,
,
,
方程无实数根,
的面积不能为;
(3)解:如图,以为坐标原点,所在直线为轴,建立平面直角坐标系,
设,,
的中点为
,
又,,
取的中点,连接,则,
,
,
,
解得:,.
【点睛】本题考查了一元二次方程的应用,勾股定理,矩形的性质,坐标与图形,一元二次方程根的判别式,两点间的距离公式,解答本题的关键是熟练掌握所涉及到的知识点并灵活运用.
典例精讲 1
典例精讲2
典例精讲3
典例精讲 1
典例精讲2
典例精讲3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
