线段的垂直平分线
图片预览


文档简介
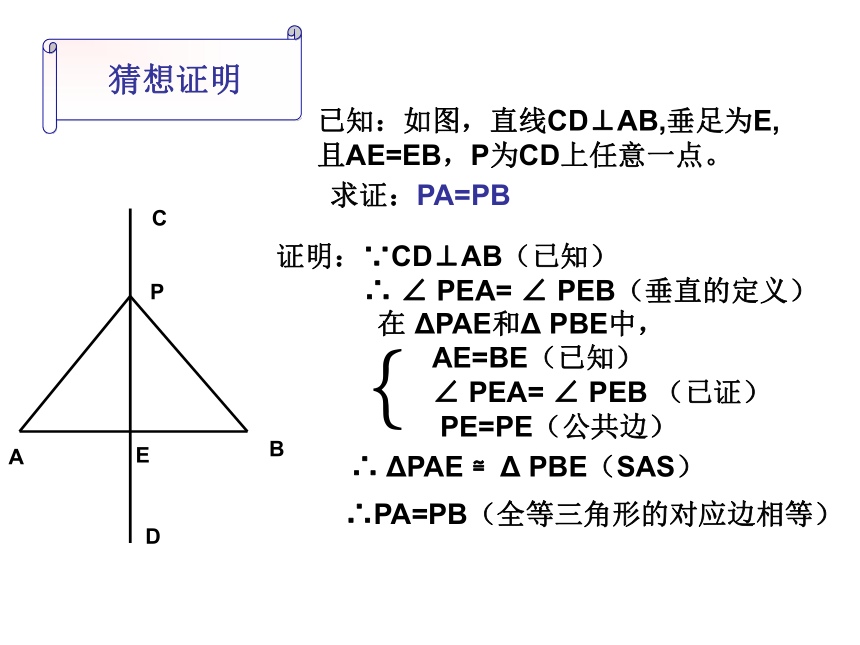
课件16张PPT。提出问题问题:有两个村庄A、B,为了便于两个村庄的人看病,乡政府计划修建一所医院,使得它到两村庄的距离相等,试问医院的院址应选在何处?AB线段的垂直平分线图形展示 已知CD是AB的垂直平分线,P是CD上任意一点,连接PA和PB,问PA=PB吗?从图形上来看,随着P点上下移动,PA=PB你能用所学过的知识来证明吗?猜想证明已知:如图,直线CD⊥AB,垂足为E,且AE=EB,P为CD上任意一点。求证:PA=PB
证明:∵CD⊥AB(已知)
∴ ∠ PEA= ∠ PEB(垂直的定义)
在 ΔPAE和Δ PBE中,
{AE=BE(已知)
∠ PEA= ∠ PEB (已证)
PE=PE(公共边)
∴ ΔPAE ≌Δ PBE(SAS)
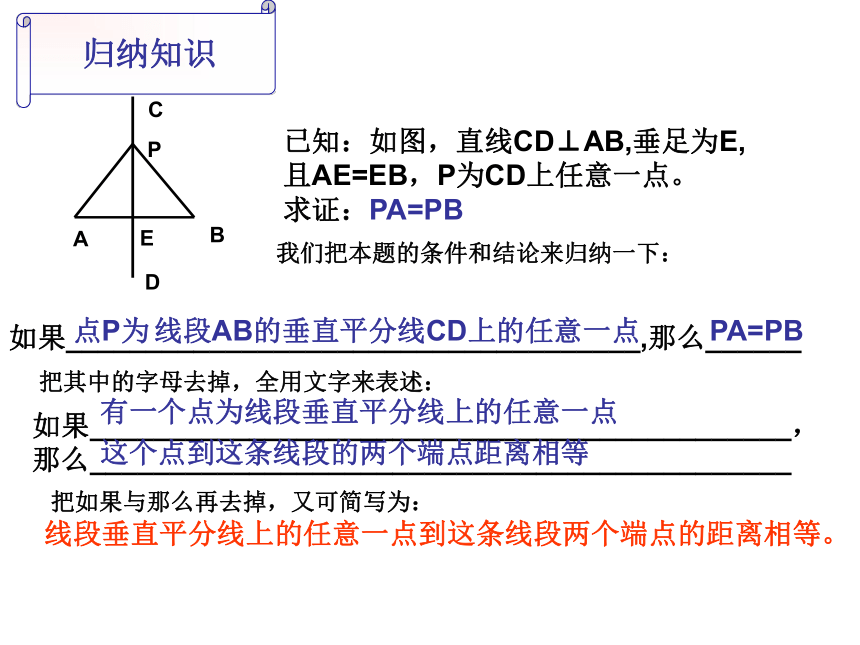
∴PA=PB(全等三角形的对应边相等)归纳知识已知:如图,直线CD⊥AB,垂足为E,且AE=EB,P为CD上任意一点。
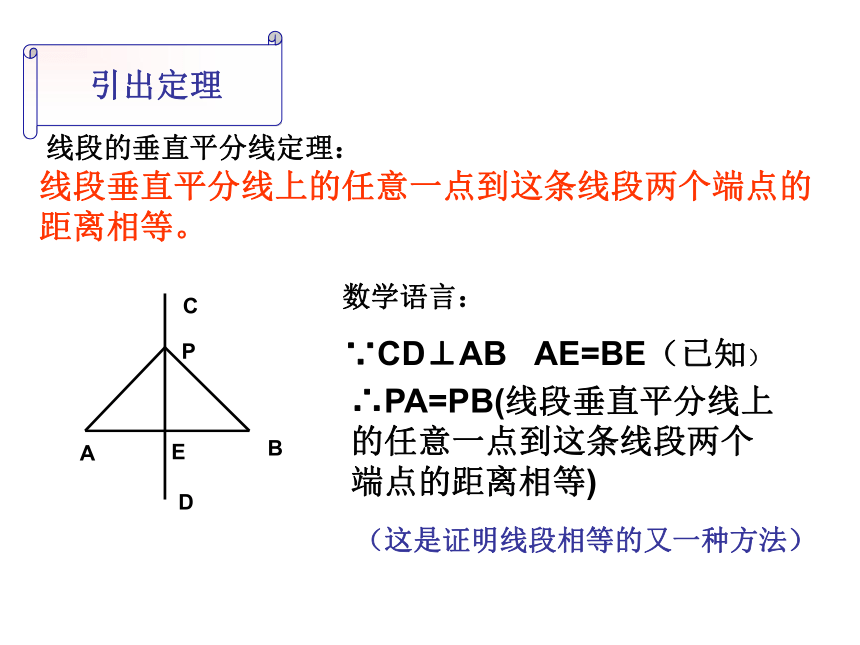
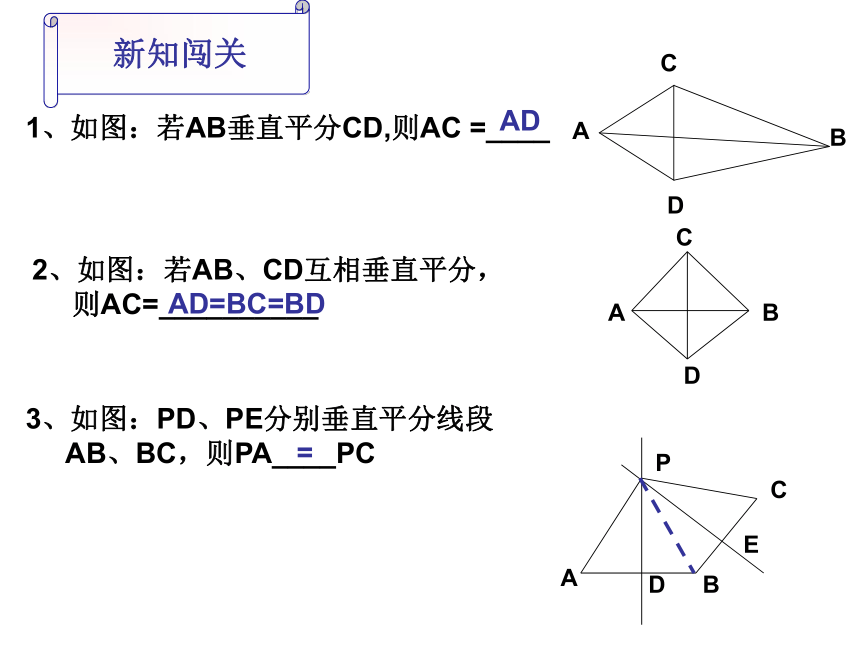
求证:PA=PB我们把本题的条件和结论来归纳一下:如果____________________________________,那么______点P为线段AB的垂直平分线CD上的任意一点PA=PB把其中的字母去掉,全用文字来表述:如果____________________________________________,那么____________________________________________有一个点为线段垂直平分线上的任意一点这个点到这条线段的两个端点距离相等把如果与那么再去掉,又可简写为:线段垂直平分线上的任意一点到这条线段两个端点的距离相等。引出定理线段的垂直平分线定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等。数学语言:∵CD⊥AB AE=BE(已知)∴PA=PB(线段垂直平分线上的任意一点到这条线段两个端点的距离相等)(这是证明线段相等的又一种方法)新知闯关1、如图:若AB垂直平分CD,则AC =____
3、如图:PD、PE分别垂直平分线段
AB、BC,则PA____PC=AD2、如图:若AB、CD互相垂直平分,
则AC=__________
AD=BC=BD4、如图:在△ABC中,已知AC=16,AB的垂直平分线交AB于点D,交AC于点E,BC=14,则△BCE的周长等于多少呢?AEBE线段垂直平分线上的任意一点到这条线段两个端点的距离相等BE+CE=1630知识延伸你能写出“定理 线段垂直平分线上的任意一点到 这条线段两个端点的距离相等”的逆命题吗?
简写为 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上它是真命题吗?
如果有一个点为线段垂直平分线上的任意一点,那么这个点到线段的两个端点距离相等。其中,题设是_________________________________结论是_________________________________ 有一个点为线段垂直平分线上的任意一点这个点到线段的两个端点距离相等逆命题是 如果_________________________________
那么_________________________________有一个点到线段的两个端点距离相等这个点为这条线段垂直平分线上的一点已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.C证明:作PC⊥AB
∵ PA=PB (已知)PC ⊥AB(已作)
∴AC=BC(等腰三角形底边上的高平分底边)
∴PC是AB的垂直平分线
即点P在AB的垂直平分线上
当P就在AB的中点上时,结论正确吗?所以,综上所述,这条逆命题是正确的,也就是说,线段的垂直平分线有它的逆定理。线段垂直平分线的逆定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
∵ PA=PB (已知)
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
数学语言:我们以后在学新的定理时,要养成这样的意识:想想它的逆命题是什么?逆命题正确吗?它有逆定理吗?要有正向的想法,也要有反向的思维。问题1:在某一乡村公路L的同侧,有两个村庄A、B,为了便于两个村庄的人看病,乡政府计划在公路边上修建一所医院,使得它到两村庄的距离相等,试问医院的院址P应选在何处?ABP联系生活问题2:有三个村庄A、B、C,为了便于三个村庄的人看病,乡政府计划修建一所医院,使得它到三个村庄的距离相等,试问医院的院址P应选在何处?P想一想,P点与BC有怎样的关系?三角形三条边的中垂线是交于一点的,这个点到三个顶点距离相等拓展研究问题3:有四个村庄A、B、C、D,乡政府计划修建一所医院,使得它到四个村庄的距离相等,试问医院的院址P选得到吗?收获小结1、学习了线段的垂直平分线的定理及逆定理
2、要培养互逆的思想
3、运用所学定理解决生活中有关的实际问题
4、要学会运用所学定理添相应的辅助线
5、初步掌握运用这两条互逆定理,解决简单 的几何论证和几何计算再见
证明:∵CD⊥AB(已知)
∴ ∠ PEA= ∠ PEB(垂直的定义)
在 ΔPAE和Δ PBE中,
{AE=BE(已知)
∠ PEA= ∠ PEB (已证)
PE=PE(公共边)
∴ ΔPAE ≌Δ PBE(SAS)
∴PA=PB(全等三角形的对应边相等)归纳知识已知:如图,直线CD⊥AB,垂足为E,且AE=EB,P为CD上任意一点。
求证:PA=PB我们把本题的条件和结论来归纳一下:如果____________________________________,那么______点P为线段AB的垂直平分线CD上的任意一点PA=PB把其中的字母去掉,全用文字来表述:如果____________________________________________,那么____________________________________________有一个点为线段垂直平分线上的任意一点这个点到这条线段的两个端点距离相等把如果与那么再去掉,又可简写为:线段垂直平分线上的任意一点到这条线段两个端点的距离相等。引出定理线段的垂直平分线定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等。数学语言:∵CD⊥AB AE=BE(已知)∴PA=PB(线段垂直平分线上的任意一点到这条线段两个端点的距离相等)(这是证明线段相等的又一种方法)新知闯关1、如图:若AB垂直平分CD,则AC =____
3、如图:PD、PE分别垂直平分线段
AB、BC,则PA____PC=AD2、如图:若AB、CD互相垂直平分,
则AC=__________
AD=BC=BD4、如图:在△ABC中,已知AC=16,AB的垂直平分线交AB于点D,交AC于点E,BC=14,则△BCE的周长等于多少呢?AEBE线段垂直平分线上的任意一点到这条线段两个端点的距离相等BE+CE=1630知识延伸你能写出“定理 线段垂直平分线上的任意一点到 这条线段两个端点的距离相等”的逆命题吗?
简写为 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上它是真命题吗?
如果有一个点为线段垂直平分线上的任意一点,那么这个点到线段的两个端点距离相等。其中,题设是_________________________________结论是_________________________________ 有一个点为线段垂直平分线上的任意一点这个点到线段的两个端点距离相等逆命题是 如果_________________________________
那么_________________________________有一个点到线段的两个端点距离相等这个点为这条线段垂直平分线上的一点已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.C证明:作PC⊥AB
∵ PA=PB (已知)PC ⊥AB(已作)
∴AC=BC(等腰三角形底边上的高平分底边)
∴PC是AB的垂直平分线
即点P在AB的垂直平分线上
当P就在AB的中点上时,结论正确吗?所以,综上所述,这条逆命题是正确的,也就是说,线段的垂直平分线有它的逆定理。线段垂直平分线的逆定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
∵ PA=PB (已知)
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
数学语言:我们以后在学新的定理时,要养成这样的意识:想想它的逆命题是什么?逆命题正确吗?它有逆定理吗?要有正向的想法,也要有反向的思维。问题1:在某一乡村公路L的同侧,有两个村庄A、B,为了便于两个村庄的人看病,乡政府计划在公路边上修建一所医院,使得它到两村庄的距离相等,试问医院的院址P应选在何处?ABP联系生活问题2:有三个村庄A、B、C,为了便于三个村庄的人看病,乡政府计划修建一所医院,使得它到三个村庄的距离相等,试问医院的院址P应选在何处?P想一想,P点与BC有怎样的关系?三角形三条边的中垂线是交于一点的,这个点到三个顶点距离相等拓展研究问题3:有四个村庄A、B、C、D,乡政府计划修建一所医院,使得它到四个村庄的距离相等,试问医院的院址P选得到吗?收获小结1、学习了线段的垂直平分线的定理及逆定理
2、要培养互逆的思想
3、运用所学定理解决生活中有关的实际问题
4、要学会运用所学定理添相应的辅助线
5、初步掌握运用这两条互逆定理,解决简单 的几何论证和几何计算再见
