5.1.2等式的性质 同步练习(含答案)
文档属性
| 名称 | 5.1.2等式的性质 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 314.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-27 21:07:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 一元一次方程
5.1 方程
5.1.2 等式的性质
基础提优题
1.下列变形正确的是( )
2.小红学习了等式的性质后,在甲、乙两台天平的左右两边分别放入“■”“●”“▲”三种物体,如图所示,天平都保持平衡.若设“■”与“●”的质量分别为x,y,则下列关系式正确的是( )
3.(1)已知等式,两边同时______________,得,依据是 ;
(2)已知等式,两边同时______________,得,依据是____________________________;
(3)已知等式两边同时_______________,得,依据是____________________________.
4.写出一个一元一次方程,要求:所写的方程必须直接利用等式两边都乘同一个数(或除以同一个不为0的数),所得的结果仍是等式求解.这样的方程可以为____________________.
5.利用等式的性质解方程:
6.阅读理解题:
下面是小明将等式进行变形的过程.
(1)①的依据是____________________;
(2)小明出错的步骤是____________(填序号),错误的原因是_____________________________________________;
(3)给出正确的解法.
综合应用题
7.下列等式变形:①如果,那么;②如果,那么③如果,那么;④如果,那么其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.一元一次方程中的部分数字被墨渍污染,翻看答案知此方程的解为,则被墨渍污染的数字“●”为( )
A.1 B.2 C.3 D.4
9.设a,b,c为互不相等的数,则下列结论正确的是( )
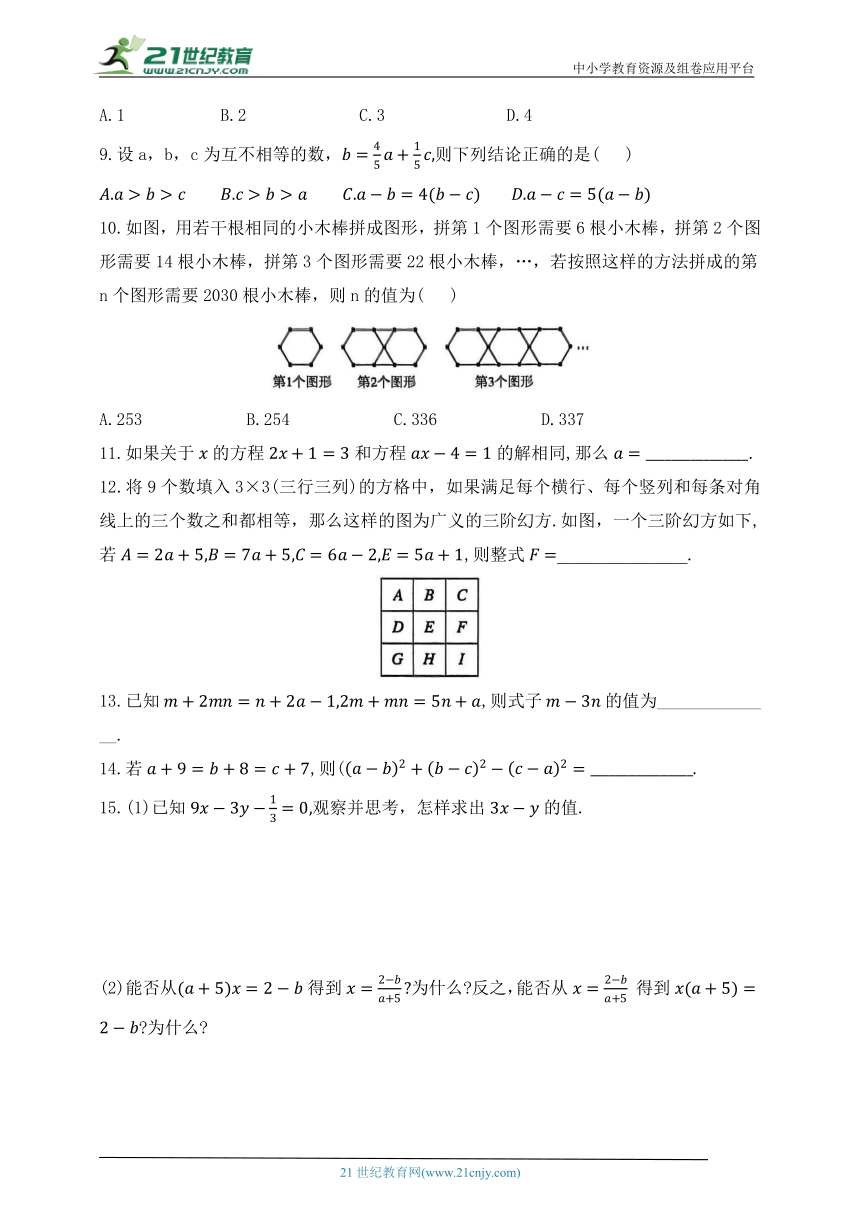
10.如图,用若干根相同的小木棒拼成图形,拼第1个图形需要6根小木棒,拼第2个图形需要14根小木棒,拼第3个图形需要22根小木棒,…,若按照这样的方法拼成的第n个图形需要2030根小木棒,则n的值为( )
A.253 B.254 C.336 D.337
11.如果关于的方程和方程的解相同,那么.
12.将9个数填入3×3(三行三列)的方格中,如果满足每个横行、每个竖列和每条对角线上的三个数之和都相等,那么这样的图为广义的三阶幻方.如图,一个三阶幻方如下,若,则整式_______________.
13.已知,则式子的值为______________.
14.若,则(
15.(1)已知观察并思考,怎样求出的值.
(2)能否从得到为什么 反之,能否从 得到 为什么
创新拓展题
16.观察下列两个等式:给出如下定义:我们称使等式a-b=2ab-1成立的一对有理数a,b为“同心有理数对”,记为(a,b).如:数对(1,),(2,)都是“同心有理数对”.根据上述材料,解答下列问题:
(1)数对(-2,1),(3,中,是“同心有理数对”的是______________.
(2)若(a,3)是“同心有理数对”,求a的值.
(3)若是“同心有理数对”,则是否为“同心有理数对” 请说明理由.
参考答案
1.C 2.C
3.(1)加3;7;等式的性质1(2)减2x;-2;等式的性质1(3)乘-5;-2;等式的性质2
4.(答案不唯一)
5.【解】(1)方程两边减5,得5+x-5=-2-5,所以x=-7.
(2)方程两边乘-2,得所以x=-8.
(3)方程两边加2x,减6,得3x+6+2x-6=31-2x+2x-6,化简,得5x=25.方程两边除以5,得x=5.
(4)方程两边加2,得0.1x-2+2=-4+2.
化简,得0.1x=-2.
方程两边乘10,得0.1x×10=-2×10.
所以x=-20.
6.【解】(1)等式的性质1
(2)③;没有确定x是否为0,就在等式的两边除以x
(3)
7.A
点易错 ,只有当a≠0时,可得x=y;a=b,只有当c≠0时,可得此题易忽略限制条件,从而错以为①②正确.
8.A
9.D【点拨】a,b,c的大小关系不能确定,所以A,B选项的结论不一定正确;的两边同时乘5,得5b=4a+c.两边同时减去4b+c,得b-c=4a-4b.两边同时乘得所以C选项的结论不正确;在5b=4a+c的两边同时减去5a,得5(b-a)=c-a.两边同时乘-1,得5(a-b)=a-c,所以D选项的结论正确.故选D.
10.B【点拨】由题意知,拼第1个图形需要6根小木棒,拼第2个图形需要6×2+2=14(根)小木棒,拼第3个图形需要6×3+2×2=22(根)小木棒,…,按此规律,拼第n个图形需要6n+2(n-1)=(8n-2)根小木棒.
令8n-2=2030,解得n=254.
11.5
12.【点拨】依题意,得
13.【点拨】因为
14.-2【点拨】因为,所以原式=
15.【解】(1)两边都加,得两边都除以3,得
(2)不能从(a+5)x=2-b得到因为当a+5=0时,两边都除以a+5,无意义,所以不能从(a+5)x=2-b得到能从得到.
因为a+5≠0,所以能从得到x(a+5)=2-b.
点易错 利用等式的两边同时乘以(或除以)同一个不为0的数,等式仍成立这一性质时,易忽略“除数不为0”这一条件导致错误.
16.【解】(1)(3,
(2)因为(a,3)是“同心有理数对”,所以a-3=6a-1.
等式两边同时减去a,得a-3-a=6a-a-1.
整理得-3=5a-1.
等式两边同时加上1,得-3+1=5a-1+1.
整理得-2=5a.
等式两边同时除以5,得
(3)(-n,-m)是“同心有理数对”.理由如下:
因为(m,n)是“同心有理数对”,所以m-n=2mn-1,而-n-(-m)=-n+m=m-n=2mn-1,所以(-n,-m)是“同心有理数对”.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 一元一次方程
5.1 方程
5.1.2 等式的性质
基础提优题
1.下列变形正确的是( )
2.小红学习了等式的性质后,在甲、乙两台天平的左右两边分别放入“■”“●”“▲”三种物体,如图所示,天平都保持平衡.若设“■”与“●”的质量分别为x,y,则下列关系式正确的是( )
3.(1)已知等式,两边同时______________,得,依据是 ;
(2)已知等式,两边同时______________,得,依据是____________________________;
(3)已知等式两边同时_______________,得,依据是____________________________.
4.写出一个一元一次方程,要求:所写的方程必须直接利用等式两边都乘同一个数(或除以同一个不为0的数),所得的结果仍是等式求解.这样的方程可以为____________________.
5.利用等式的性质解方程:
6.阅读理解题:
下面是小明将等式进行变形的过程.
(1)①的依据是____________________;
(2)小明出错的步骤是____________(填序号),错误的原因是_____________________________________________;
(3)给出正确的解法.
综合应用题
7.下列等式变形:①如果,那么;②如果,那么③如果,那么;④如果,那么其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.一元一次方程中的部分数字被墨渍污染,翻看答案知此方程的解为,则被墨渍污染的数字“●”为( )
A.1 B.2 C.3 D.4
9.设a,b,c为互不相等的数,则下列结论正确的是( )
10.如图,用若干根相同的小木棒拼成图形,拼第1个图形需要6根小木棒,拼第2个图形需要14根小木棒,拼第3个图形需要22根小木棒,…,若按照这样的方法拼成的第n个图形需要2030根小木棒,则n的值为( )
A.253 B.254 C.336 D.337
11.如果关于的方程和方程的解相同,那么.
12.将9个数填入3×3(三行三列)的方格中,如果满足每个横行、每个竖列和每条对角线上的三个数之和都相等,那么这样的图为广义的三阶幻方.如图,一个三阶幻方如下,若,则整式_______________.
13.已知,则式子的值为______________.
14.若,则(
15.(1)已知观察并思考,怎样求出的值.
(2)能否从得到为什么 反之,能否从 得到 为什么
创新拓展题
16.观察下列两个等式:给出如下定义:我们称使等式a-b=2ab-1成立的一对有理数a,b为“同心有理数对”,记为(a,b).如:数对(1,),(2,)都是“同心有理数对”.根据上述材料,解答下列问题:
(1)数对(-2,1),(3,中,是“同心有理数对”的是______________.
(2)若(a,3)是“同心有理数对”,求a的值.
(3)若是“同心有理数对”,则是否为“同心有理数对” 请说明理由.
参考答案
1.C 2.C
3.(1)加3;7;等式的性质1(2)减2x;-2;等式的性质1(3)乘-5;-2;等式的性质2
4.(答案不唯一)
5.【解】(1)方程两边减5,得5+x-5=-2-5,所以x=-7.
(2)方程两边乘-2,得所以x=-8.
(3)方程两边加2x,减6,得3x+6+2x-6=31-2x+2x-6,化简,得5x=25.方程两边除以5,得x=5.
(4)方程两边加2,得0.1x-2+2=-4+2.
化简,得0.1x=-2.
方程两边乘10,得0.1x×10=-2×10.
所以x=-20.
6.【解】(1)等式的性质1
(2)③;没有确定x是否为0,就在等式的两边除以x
(3)
7.A
点易错 ,只有当a≠0时,可得x=y;a=b,只有当c≠0时,可得此题易忽略限制条件,从而错以为①②正确.
8.A
9.D【点拨】a,b,c的大小关系不能确定,所以A,B选项的结论不一定正确;的两边同时乘5,得5b=4a+c.两边同时减去4b+c,得b-c=4a-4b.两边同时乘得所以C选项的结论不正确;在5b=4a+c的两边同时减去5a,得5(b-a)=c-a.两边同时乘-1,得5(a-b)=a-c,所以D选项的结论正确.故选D.
10.B【点拨】由题意知,拼第1个图形需要6根小木棒,拼第2个图形需要6×2+2=14(根)小木棒,拼第3个图形需要6×3+2×2=22(根)小木棒,…,按此规律,拼第n个图形需要6n+2(n-1)=(8n-2)根小木棒.
令8n-2=2030,解得n=254.
11.5
12.【点拨】依题意,得
13.【点拨】因为
14.-2【点拨】因为,所以原式=
15.【解】(1)两边都加,得两边都除以3,得
(2)不能从(a+5)x=2-b得到因为当a+5=0时,两边都除以a+5,无意义,所以不能从(a+5)x=2-b得到能从得到.
因为a+5≠0,所以能从得到x(a+5)=2-b.
点易错 利用等式的两边同时乘以(或除以)同一个不为0的数,等式仍成立这一性质时,易忽略“除数不为0”这一条件导致错误.
16.【解】(1)(3,
(2)因为(a,3)是“同心有理数对”,所以a-3=6a-1.
等式两边同时减去a,得a-3-a=6a-a-1.
整理得-3=5a-1.
等式两边同时加上1,得-3+1=5a-1+1.
整理得-2=5a.
等式两边同时除以5,得
(3)(-n,-m)是“同心有理数对”.理由如下:
因为(m,n)是“同心有理数对”,所以m-n=2mn-1,而-n-(-m)=-n+m=m-n=2mn-1,所以(-n,-m)是“同心有理数对”.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
