六年级暑假新课预习提升练第七单元检测卷《扇形统计图》(含解析)-2024-2025学年下学期小学数学 人教版
文档属性
| 名称 | 六年级暑假新课预习提升练第七单元检测卷《扇形统计图》(含解析)-2024-2025学年下学期小学数学 人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 727.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-27 21:50:26 | ||
图片预览


文档简介
六年级暑假新课预习提升练第七单元检测卷《扇形统计图》(含解析)-2024-2025学年下学期小学数学人教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.妈妈想清楚地表示家里每月收入与各项消费的支出、储蓄理财等之间的关系,应该选用( )统计图比较好。
A.扇形 B.折线 C.条形 D.以上三种统计图任选一个
2.扇形统计图能清楚地表示( )。
A.数量的多少 B.数量的多少和增减变化的情况
C.部分数量与总数量之间的关系 D.各部分的具体量
3.光明小学少先队投票选举大队长。4名候选人的得票结果是:小明100票,小亮50票,小红30票,小丽20票。下面四幅图中,能准确表示这一结果的是( )。
A. B. C. D.
4.某市六月份的天气情况如图所示,则本月的晴天有( )天。
A.3 B.9 C.18
5.红红家上月的教育支出是全月总支出的15%,绘制她家上月支出情况的扇形统计图时画出教育支出的扇形圆心角应该是( )°。
A.15 B.30 C.54 D.105
6.下面说法正确的是( )。
A.大圆的圆周率比小圆的圆周率大。
B.用4个圆心角是90°的扇形,一定能拼成一个圆。
C.扇形的大小与其半径的长短、圆心角的大小有关。
D.要表示一个地区降水量的增减变化情况,用扇形统计图表示最合适。
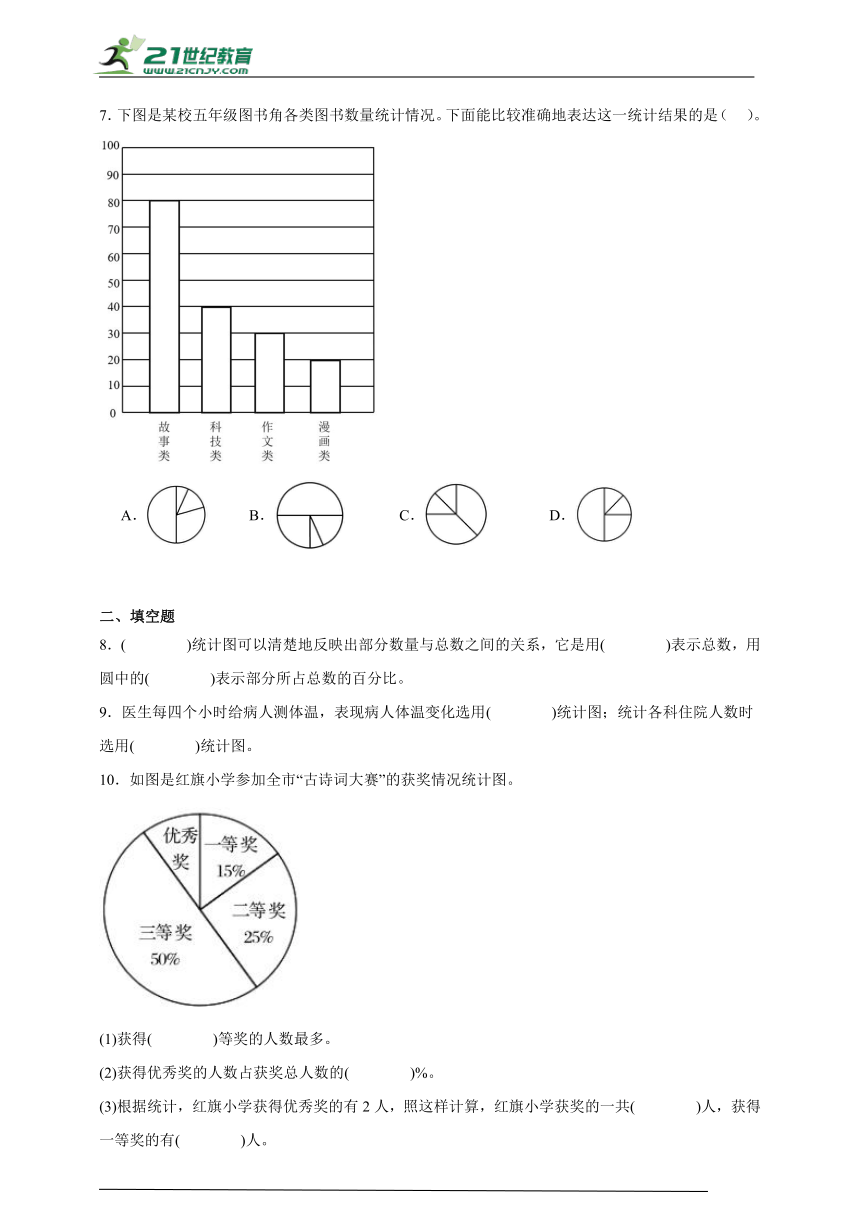
7.下图是某校五年级图书角各类图书数量统计情况。下面能比较准确地表达这一统计结果的是( )。
A. B. C. D.
二、填空题
8.( )统计图可以清楚地反映出部分数量与总数之间的关系,它是用( )表示总数,用圆中的( )表示部分所占总数的百分比。
9.医生每四个小时给病人测体温,表现病人体温变化选用( )统计图;统计各科住院人数时选用( )统计图。
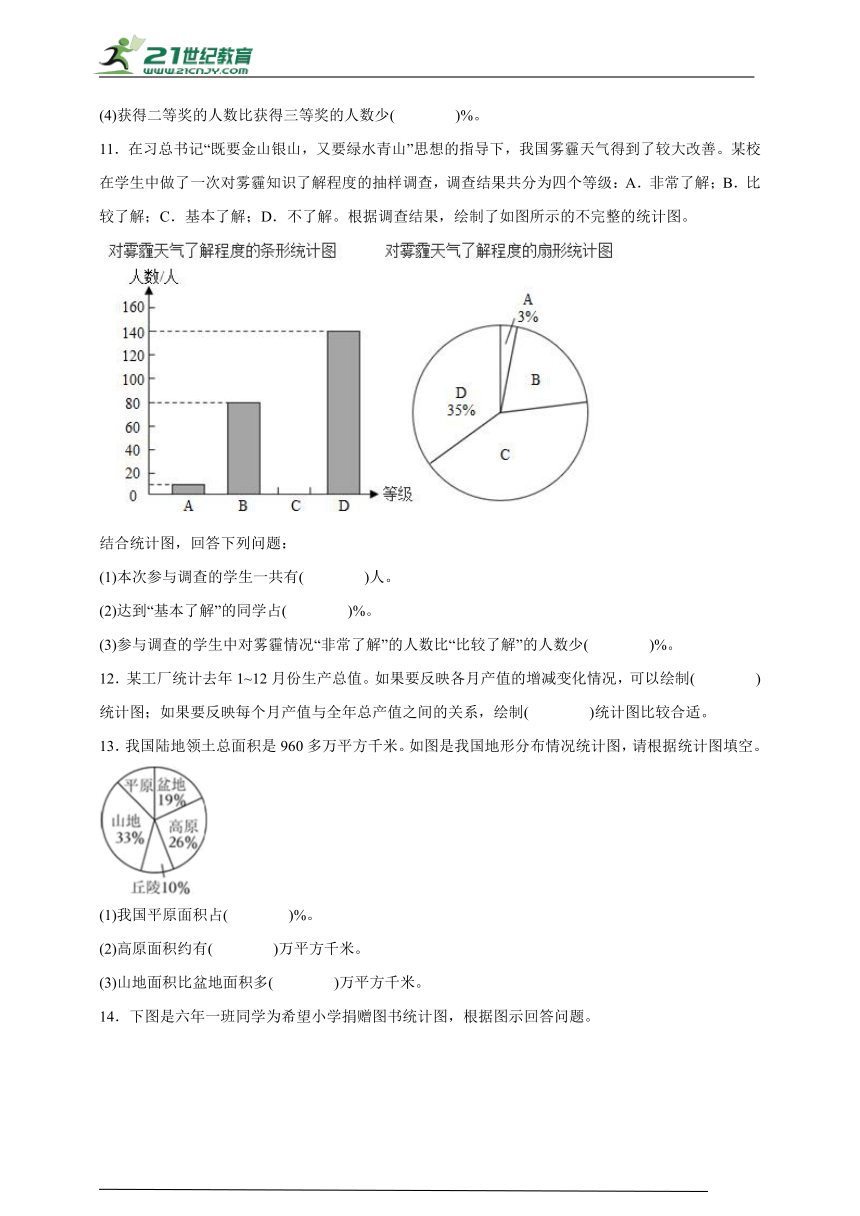
10.如图是红旗小学参加全市“古诗词大赛”的获奖情况统计图。
(1)获得( )等奖的人数最多。
(2)获得优秀奖的人数占获奖总人数的( )%。
(3)根据统计,红旗小学获得优秀奖的有2人,照这样计算,红旗小学获奖的一共( )人,获得一等奖的有( )人。
(4)获得二等奖的人数比获得三等奖的人数少( )%。
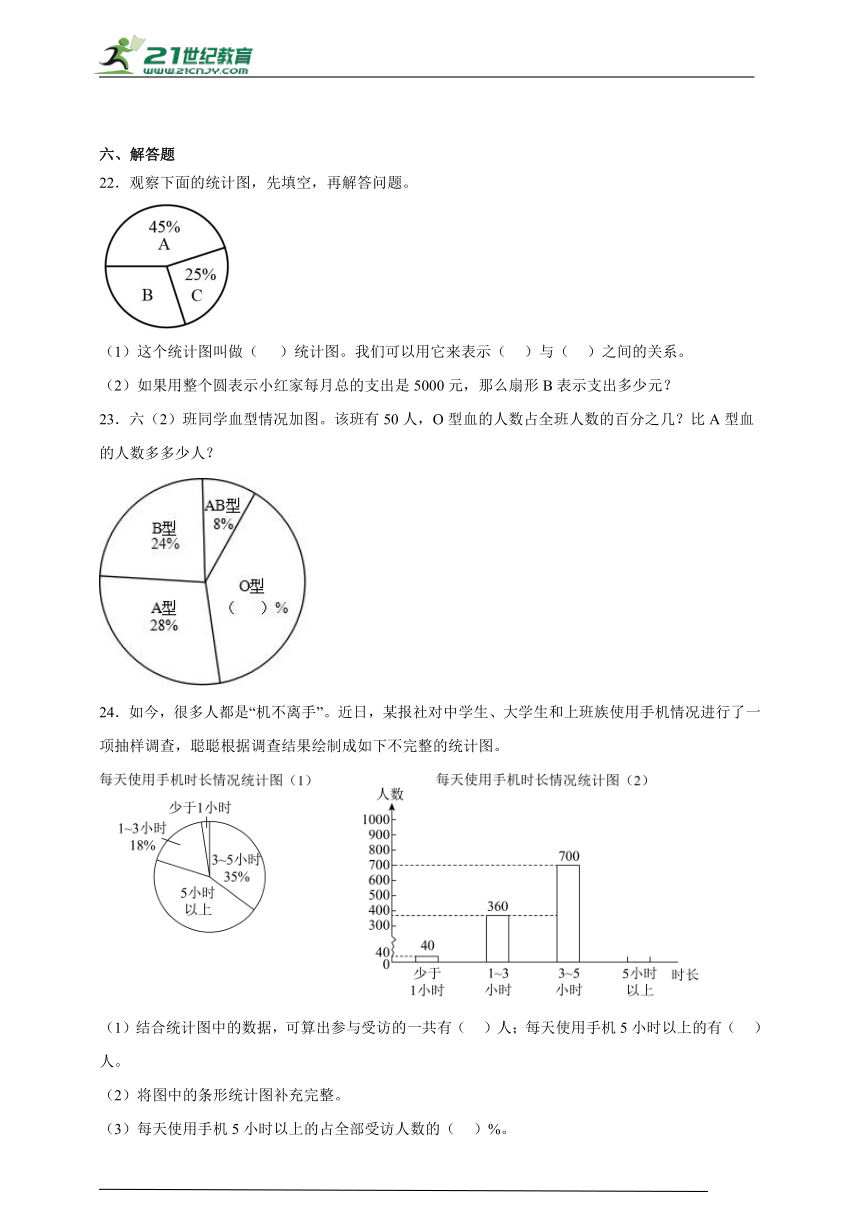
11.在习总书记“既要金山银山,又要绿水青山”思想的指导下,我国雾霾天气得到了较大改善。某校在学生中做了一次对雾霾知识了解程度的抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解。根据调查结果,绘制了如图所示的不完整的统计图。
结合统计图,回答下列问题:
(1)本次参与调查的学生一共有( )人。
(2)达到“基本了解”的同学占( )%。
(3)参与调查的学生中对雾霾情况“非常了解”的人数比“比较了解”的人数少( )%。
12.某工厂统计去年1~12月份生产总值。如果要反映各月产值的增减变化情况,可以绘制( )统计图;如果要反映每个月产值与全年总产值之间的关系,绘制( )统计图比较合适。
13.我国陆地领土总面积是960多万平方千米。如图是我国地形分布情况统计图,请根据统计图填空。
(1)我国平原面积占( )%。
(2)高原面积约有( )万平方千米。
(3)山地面积比盆地面积多( )万平方千米。
14.下图是六年一班同学为希望小学捐赠图书统计图,根据图示回答问题。
(1)捐赠的科技类图书占捐赠图书总数的( )%;
(2)如果捐赠的文学类图书有20本,则捐赠的科幻类图书有( )本。
三、判断题
15.从扇形统计图中可以看出各部分数量的多少。( )
16.扇形统计图中各部分百分比的和一定是100%。( )
17.要反映某小学本学期六年级数学月考成绩变化情况,应选择扇形统计图。( )
18.面粉中含有蛋白质、脂肪、糖类等营养物质,要表示各种成分的含量占总量的百分比的情况,应选择扇形统计图更合适。( )
19.要表示出六年级各班学生人数的情况,绘制折线统计图更直观。( )
四、计算题
20.一个数减少它的15%后是5.1,这个数是多少?(用方程解)
五、作图题
21.学校抽查了若干名小学生的坐姿、站姿、走姿的好坏情况(每个学生只记录最突出的一种),并将统计结果绘成如下两幅不完整的统计图。
(1)请将两幅统计图补充完整。
(2)一共抽查了_________人,其中站姿不良的学生人数比坐姿不良的学生人数少_________%。
(3)如该市共有学生14000人,则该市小学生中“三姿”良好的学生有_________人。
六、解答题
22.观察下面的统计图,先填空,再解答问题。
(1)这个统计图叫做( )统计图。我们可以用它来表示( )与( )之间的关系。
(2)如果用整个圆表示小红家每月总的支出是5000元,那么扇形B表示支出多少元?
23.六(2)班同学血型情况加图。该班有50人,O型血的人数占全班人数的百分之几?比A型血的人数多多少人?
24.如今,很多人都是“机不离手”。近日,某报社对中学生、大学生和上班族使用手机情况进行了一项抽样调查,聪聪根据调查结果绘制成如下不完整的统计图。
(1)结合统计图中的数据,可算出参与受访的一共有( )人;每天使用手机5小时以上的有( )人。
(2)将图中的条形统计图补充完整。
(3)每天使用手机5小时以上的占全部受访人数的( )%。
(4)88.5%的受访者坦言最近使用手机时长增加了,主要是刷短视频、网上购物和沟通工作。由于长时间观看手机屏幕会使眼睛疲劳、干涩,引发视力下降,所以养成良好的手机使用习惯很重要。对此,你有什么好的建议?(至少写出两条)
25.下图是实验一小六年级参加课后托管情况,他们分别参加体育、科技、音乐和其他四个类别的活动(每位同学只参加一项)。经过调查后,统计了他们参加四项活动的情况,并制成条形统计图和扇形统计图。
(1)请你根据图中数据,计算科技组的人数(填在方框中)。
(2)请在图中用条形表示音乐组的人数。
26.垃圾分类有利于改善城乡环境,保障人体健康,维护生态安全。垃圾的种类有可回收物,厨余垃圾,有害垃圾和其他垃圾。同学们对某小区一周产生的垃圾构成情况进行了调查,请你根据统计图完成下面的问题。
(1)这个小区这周一共产生垃圾多少吨?
(2)可回收垃圾有多少吨?请把条形统计图补充完整。
《六年级暑假新课预习提升练第七单元检测卷《扇形统计图》(含解析)-2024-2025学年下学期小学数学人教版》参考答案
题号 1 2 3 4 5 6 7
答案 A C C C C C B
1.A
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;
扇形统计图表示各部分数量与总数之间的关系。
【详解】妈妈想清楚地表示家里每月收入与各项消费的支出、储蓄理财等之间的关系,应该选用扇形统计图比较好。
故答案为:A
【点睛】理解掌握条形统计图、折线统计图、扇形统计图的特点是选择统计图的关键。
2.C
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此解答。
【详解】扇形统计图能清楚地表示部分数量与总数量之间的关系。
故答案为:C
3.C
【分析】先用加法求出总票数,再用小明、小亮、小红、小丽的得票数分别除以总票数再乘100%得出这四个人所占的百分比,从而判断出哪个扇形图是正确的,据此解答即可。
【详解】100+50+30+20
=150+30+20
=180+20
=200(票)
小明:100÷200×100%
=0.5×100%
=50%
小亮:50÷200×100%
=0.25×100%
=25%
小红:30÷200×100%
=0.15×100%
=15%
小丽:20÷200×100%
=0.1×100%
=10%
因此,选项C的图能准确表示这一结果。
故答案为:C
4.C
【分析】六月份有30天,晴天的天数占六月份天数的60%,根据求一个数的百分之几是多少,用乘法计算,即用30乘60%即可求解。
【详解】30×60%=18(天)
则本月的晴天有18天。
故答案为:C
5.C
【分析】根据扇形统计图的特点,用圆的面积表示全月总支出,圆周角是360°,教育支出占全月总支出的15%,也就是说教育支出的扇形圆心角占360°的15%,根据求一个数的百分之几是多少,用乘法计算,即可求出教育支出的扇形圆心角。
【详解】360°×15%
=360°×0.15
=54°
绘制她家上月支出情况的扇形统计图时画出教育支出的扇形圆心角应该是54°。
故答案为:C
【点睛】本题考查扇形统计图的特点及百分数乘法的应用,已知部分占总量的百分之几,也就是扇形的圆心角占360°的百分之几。
6.C
【分析】A.圆周率不会因为圆的大小而变化。
B.用4个半径相同,圆心角都是90°的扇形,能拼成一个圆。
C.根据圆形的面积=πr2,扇形的面积=πr2,扇形的大小与其半径的长短、圆心角的大小有关。
D.折线统计图特点是用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。要表示一个地区降水量的增减变化情况,用折线统计图表示最合适。
【详解】A.圆周率不因圆的大小而变化,所以原选项说法错误;
B.用4个半径相同,圆心角都是90°的扇形,才能拼成一个圆,所以原选项说法错误;
C.扇形的大小与其半径的长短、圆心角的大小有关,选项说法正确;
D.要表示一个地区降水量的增减变化情况,用折线统计图表示最合适,所以原选项说法错误。
故答案为:C
7.B
【分析】从条形统计图中可知,故事类图书有80本,科技类图书有40本,作文类图书有30本,漫画类图书有10本,一共有(80+40+30+10)本,用各类图书的本数除以总本数,求出各类图书占总本数的百分比,也就是各类图书的扇形面积占整个圆面积的百分比,结合各选项中的扇形统计图得出结论。
【详解】图书总数:80+40+30+10=160(本)
故事类图书占总本数的:80÷160×100%=50%
科技类图书占总本数的:40÷160×100%=25%
作文类图书占总本数的:30÷160×100%=18.75%
漫画类图书占总本数的:10÷160×100%=6.25%
50%>25%>18.75%>6.25%
A.图中第二大扇形的面积占整个圆的百分比>25%,不符合题意;
B.图中最大扇形的面积占整个圆的50%,第二大扇形的面积占整个圆的25%,剩下的两个小扇形也有大小区分,所以这个扇形统计图能准确表达这一统计结果;
C.图中最大扇形的面积占整个圆的百分比<50%,第二大扇形的面积占整个圆的百分比>25%,不符合题意;
D.图中两个小的扇形面积一样大,不符合题意。
故答案为:B
【点睛】理解掌握条形统计图、扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
8. 扇形 圆 扇形
【详解】扇形统计图可以清楚地反映出部分数量与总数之间的关系,它是用圆表示总数,用圆中的扇形表示部分所占总数的百分比。
如:我国陆地各种地形所占百分比:
9. 折线 条形
【分析】条形统计图可以直观地显示数量的多少。
折线统计图除了显示数量的多少,还可以清楚地反应数量的增减变化情况。
扇形统计图可以清楚地看出各部分数量和总数量之间的关系。
根据各种统计图的特点,选择合适的统计图,据此解答。
【详解】由分析得:
表现病人体温变化选用折线统计图;统计各科住院人数时选用条形统计图。
10.(1)三
(2)10
(3) 20 3
(4)50
【分析】(1)观察扇形统计图,哪个奖项所占的区域最大,那么获得这个奖项的人数就最多。
(2)把获奖总人数看作单位“1”,用“1”减去获得一等奖、二等奖、三等奖的人数分别占获奖总人数的百分比,即是获得优秀奖的人数占获奖总人数的百分之几。
(3)把获奖总人数看作单位“1”,已知获得优秀奖的有2人占获奖总人数的10%,单位“1”未知,用获得优秀奖的人数除以10%,即可求出获奖总人数;
从图中可知,获得一等奖的人数占获奖总人数的15%,根据求一个数的百分之几是多少,用获奖总人数乘15%,即是获得一等奖的人数。
(4)从图中可知,获得二等奖、三等奖的人数分别占获奖总人数的25%、50%,先用减法求出少的量,再除以获得三等奖占获奖总人数的百分比即可。
【详解】(1)获得三等奖的人数最多。
(2)1-15%-25%-50%=10%
获得优秀奖的人数占获奖总人数的10%。
(3)2÷10%
=2÷0.1
=20(人)
20×15%
=20×0.15
=3(人)
红旗小学获奖的一共20人,获得一等奖的有3人。
(4)(50%-25%)÷50%×100%
=(0.5-0.25)÷0.5×100%
=0.25÷0.5×100%
=0.5×100%
=50%
获得二等奖的人数比获得三等奖的人数少50%。
11.(1)400
(2)42
(3)87.5
【分析】(1)把调查的总人数看作单位“1”,不了解的有140人,占调查总人数的35%,根据已知一个数的百分之几是多少,求这个数,用除法解答;
(2)用比较了解的人数除以总人数,得出比较了解的人数占的百分率,再用减法计算即可得C部分基本了解占的百分率;
(3)用“比较了解”的人数减“非常了解”的人数,再除以“比较了解”的人数即可。
【详解】(1)140÷35%=400(人)
(2)80÷400×100%
=0.2×100%
=20%
1-3%-20%-35%
=97%-20%-35%
=77%-35%
=42%
(3)(80-10)÷80×100%
=70÷80×100%
=0.875×100%
=87.5%
【点睛】此题主要考查学生如何从扇形统计图、条形统计图中获取信息,然后再根据所获取的信息解决实际问题。
12. 折线 扇形
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】某工厂统计去年1~12月份生产总值。如果要反映各月产值的增减变化情况,可以绘制折线统计图;如果要反映每个月产值与全年总产值之间的关系,绘制扇形统计图比较合适。
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
13.(1)12
(2)249.6
(3)134.4
【分析】(1)把我国陆地总面积看作单位“1”,根据减法的意义,用1减去山地、盆地、丘陵、高原占总面积的百分率,即可解答。
(2)根据求一个数的百分之几是多少,用陆地领土总面积乘高原占总面积的百分率即可解答。
(3)先求出山地面积比盆地面积多占总面积的百分之几,然后根据求一个数的百分之几是多少,用乘法解答。
【详解】(1)1-33%-10%-26%-19%
=67%-10%-26%-19%
=57%-26%-19%
=31%-19%
=12%
我国平原面积占12%。
(2)960×26%=249.6(万平方千米)
高原面积约有249.6万平方千米。
(3)960×(33%-19%)
=960×14%
=134.4(万平方千米)
山地面积比盆地面积多134.4万平方千米。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
14.(1)25
(2)8
【分析】(1)从扇形统计图中可知,科技类图书的扇形的圆心角是90°,占整个圆的,化成小数是0.25,再化成百分数是25%,即可求解。
(2)把图书的总数看作单位“1”,从扇形统计图中可知,文学类图书的扇形占整个图的一半,即20本文学类图书占图书总数的50%,单位“1”未知,用文学类图书的本数除以50%,即可求出图书的总数;
图书的总数是单位“1”,用“1”减去科技类、文学类、童话类占总数的百分比之和,即是科幻类图书占总数的百分比;单位“1”已知,用图书总数乘科幻类图书的百分比,求出科幻类图书的本数。
【详解】(1)=0.25=25%
捐赠的科技类图书占捐赠图书总数的25%。
(2)图书的总数:
20÷50%
=20÷0.5
=40(本)
科幻类图书占图书总数的:
1-(25%+50%+5%)
=1-80%
=20%
科幻类图书有:
40×20%
=40×0.2
=8(本)
【点睛】本题考查百分数的应用,根据扇形统计图提供的信息,解决有关的百分数问题。明确已知一个数的百分之几是多少,求这个数,用除法计算;求一个数的百分之几是多少,用乘法计算。
15.×
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;
扇形统计图表示各部分数量与总数之间的关系或各部分与各部分之间的关系。
【详解】从扇形统计图中可以看出各部分数量与总数之间的关系。
原题说法错误。
故答案为:×
【点睛】本题考查扇形统计图的特点。
16.√
【分析】在扇形统计图中,整个圆代表总体,把总体看作单位“1”,每个扇形代表总体中的各部分,各部分之和等于单位“1”,即各部分数量占总数的百分比的总和都是100%。
【详解】分析可知,任何扇形统计图中,各部分数量占总数的百分比的总和都是100%。
故答案为:√
【点睛】扇形统计图是用圆的面积表示总数,用圆内扇形的面积表示各部分占总数的百分比。
17.×
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况解答即可。
【详解】要反映某小学本学期六年级数学月考成绩变化情况,应选择折线统计图。
故答案为:×
【点睛】此题根据扇形统计图、折线统计图、条形统计图各自的特点来判断。
18.√
【分析】扇形统计图是以一个圆的面积(看作单位“1”)表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数的统计图。
【详解】面粉中含有蛋白质、脂肪、糖类等营养物质,要表示各种成分的含量占总量的百分比的情况,应选择扇形统计图更合适,说法正确。
故答案为:√
【点睛】扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系。
19.×
【分析】条形统计图的特点是能清楚地表示出各种数量的多少;折线统计图的特点是既能表示出各种数量的多少,又能表示出数量的增减变化情况;扇形统计图的特点是能从图中清楚地看出各部分数量占总数的百分比,以及部分与部分之间的关系。根据要反映的信息,结合三种统计图的特点选择统计图。
【详解】根据三种统计图的特点,要表示出六年级各班学生人数的情况,绘制条形统计图更直观。
故答案为:×
【点睛】区别不同统计图的应用范围是解决此题的关键。
20.6
【分析】求一个数的百分之几是多少用乘法,设这个数是x,根据这个数-这个数×15%=5.1,列出方程求出x的值即可。
【详解】解:设这个数是x。
x-15%x=5.1
0.85x=5.1
0.85x÷0.85=5.1÷0.85
x=6
这个数是6。
21.(1)见详解
(2)500;40
(3)4200
【分析】(1)把学校抽查的若干名小学生的人数看作单位“1”,用1减去坐姿、站姿、走姿不良的人数占被抽查的百分率,就是三姿良好的人数占的百分率,据此补充扇形统计图;已知一个数的百分之几是多少,求这个数用除法,由条形统计图可知,坐姿不良的人数是100,由扇形统计图可知,坐姿不良的人数占单位“1”的20%,用100÷20%列式求出学校抽查的若干名小学生的人数,根据求一个数的百分之几是多少,用乘法,用学校抽查的若干名小学生的人数乘三姿良好的人数占的百分率,求出三姿良好的人数,据此补充条形统计图;
(2)由(1)可知一共抽查的人数;求一个数比另一个数少百分之几,用两个数的差除以另一个数,据此用坐姿不良的学生人数占抽查人数的百分率减去坐姿不良的学生人数占抽查人数的百分率,再除以坐姿不良的学生人数占抽查人数的百分率即可解答;
(3)把该市共有学生的总人数看作单位“1”,求一个数的百分之几是多少,用乘法解答,用14000乘三姿”良好的学生占的百分率即可解答。
【详解】(1)1-20%-12%-38%
=80%-12%-38%
=68%-38%
=30%
100÷20%=500(人)
500×30%=150(人)
如图:
(2)由(1)可知:一共抽查了500人;
(20%-12%)÷20%
=0.08÷0.2
=40%
所以一共抽查了500人,其中站姿不良的学生人数比坐姿不良的学生人数少40%。
(3)14000×30%=4200(人)
所以该市小学生中“三姿”良好的学生有4200人。
22.(1)扇形;部分;整体;(2)1500元
【分析】(1)扇形统计图是以一个圆的面积(看作单位“1”)表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数的统计图。
(2)把小红家每月总支出看作单位“1”,用1减去A项、C项的支出占总支出的百分比,即可求出扇形B占总支出的百分比,求一个数的百分之几是多少,用乘法,用小红家每月总支出5000元乘扇形B占总支出的百分比,即可求出扇形B支出多少元。
【详解】(1)这个统计图叫做扇形统计图。我们可以用它来表示部分与整体之间的关系。
(2)5000×(1-45%-25%)
=5000×(1-0.45-0.25)
=5000×0.3
=1500(元)
答:扇形B表示支出1500元。
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
23.40%;6人
【分析】把该班总人数看作单位“1”,用减法计算即可得O型血的人数占全班人数的百分之几;用该班的总人数分别乘O型血的人数和A型血的人数占总人数的百分率,再相减即可。
【详解】1-24%-28%-8%
=76%-28%-8%
=40%
50×40%-50×28%
=20-14
=6(人)
答:O型血的人数占全班人数的40%,O型血的人数比A型血的人数多6人。
【点睛】此题主要考查的是如何从扇形统计图中获取信息,然后再根据信息进行计算的能力。
24.(1)2000;900
(2)见详解
(3)45
(4)见详解
【分析】(1)观察可知,把参与受访总人数看作单位“1”,已知1-3小时有360人占总人数的18%,根据已知一个数的百分之几是多少,求这个数用除法计算,可得参与受访总人数;用总人数减去其它三个时间段的人数可得5小时以上的人数。
(2)观察可知条形统计图的横轴表示时长,纵轴表示人数,纵轴每格表示100人,据此画出表示5小时以上的人数的直条即可。
(3)根据求一个数占另一个数的百分之几,用除法计算,用每天使用手机5小时以上的除以全部受访人数。
(4)由题可知:过渡使用手机是造成视力问题的主要原因,所以建议从合理控制使用手机时长,多做户外运动等方面提出即可。
【详解】(1)(人)
(人)
结合统计图中的数据,可算出参与受访的一共有2000人;每天使用手机5小时以上的有900人。
(2)如下图:
(3)
每天使用手机5小时以上的占全部受访人数的45%。
(4)答:1.减少手机的使用时间,用眼一段时间后做眼保健操放松眼睛,避免用眼过渡;2.多参加户外运动。(答案唯一)
25.(1)30人
(2)见详解
【分析】(1)将总人数看作“1”,体育组人数÷对应百分率=总人数,总人数×科技组对应百分率=科技组人数。
(2)1-体育组对应百分率-科技组对应百分率-其他组对应百分率=音乐组对应百分率,总人数×音乐组对应百分率=音乐组人数,据此补充条形统计图。
【详解】(1)48÷40%×25%
=48÷0.4×0.25
=30(人)
(2)48÷40%×(1-40%-25%-15%)
=48÷0.4×0.2
=24(人)
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
26.(1)40吨;(2)10吨;见详解。
【分析】(1)厨余垃圾是22吨,厨余垃圾占这周垃圾总吨数的55%,已知一个数的百分之几是多少,求这个数,用除法,列式:22÷55%,即可求出这个小区这周一共产生的垃圾总吨数。
(2)把这周垃圾总吨数看作单位“1”,用1连续减去厨余垃圾、有害垃圾和其他垃圾占垃圾总吨数的百分比,即可求得可回收物占这周垃圾总吨数的百分比,再用这周垃圾总吨数乘可回收物占这周垃圾总吨数的百分比,即可求出可回收垃圾的吨数。并把数据补充到条形统计图中。
【详解】(1)22÷55%=40(吨)
答:这个小区这周一共产生垃圾40吨。
(2)1-16%-4%-55%=25%
40×25%=10(吨)
答:可回收垃圾有10吨。
补充如下:
【点睛】此题考查的目的是理解掌握条形统计图和扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.妈妈想清楚地表示家里每月收入与各项消费的支出、储蓄理财等之间的关系,应该选用( )统计图比较好。
A.扇形 B.折线 C.条形 D.以上三种统计图任选一个
2.扇形统计图能清楚地表示( )。
A.数量的多少 B.数量的多少和增减变化的情况
C.部分数量与总数量之间的关系 D.各部分的具体量
3.光明小学少先队投票选举大队长。4名候选人的得票结果是:小明100票,小亮50票,小红30票,小丽20票。下面四幅图中,能准确表示这一结果的是( )。
A. B. C. D.
4.某市六月份的天气情况如图所示,则本月的晴天有( )天。
A.3 B.9 C.18
5.红红家上月的教育支出是全月总支出的15%,绘制她家上月支出情况的扇形统计图时画出教育支出的扇形圆心角应该是( )°。
A.15 B.30 C.54 D.105
6.下面说法正确的是( )。
A.大圆的圆周率比小圆的圆周率大。
B.用4个圆心角是90°的扇形,一定能拼成一个圆。
C.扇形的大小与其半径的长短、圆心角的大小有关。
D.要表示一个地区降水量的增减变化情况,用扇形统计图表示最合适。
7.下图是某校五年级图书角各类图书数量统计情况。下面能比较准确地表达这一统计结果的是( )。
A. B. C. D.
二、填空题
8.( )统计图可以清楚地反映出部分数量与总数之间的关系,它是用( )表示总数,用圆中的( )表示部分所占总数的百分比。
9.医生每四个小时给病人测体温,表现病人体温变化选用( )统计图;统计各科住院人数时选用( )统计图。
10.如图是红旗小学参加全市“古诗词大赛”的获奖情况统计图。
(1)获得( )等奖的人数最多。
(2)获得优秀奖的人数占获奖总人数的( )%。
(3)根据统计,红旗小学获得优秀奖的有2人,照这样计算,红旗小学获奖的一共( )人,获得一等奖的有( )人。
(4)获得二等奖的人数比获得三等奖的人数少( )%。
11.在习总书记“既要金山银山,又要绿水青山”思想的指导下,我国雾霾天气得到了较大改善。某校在学生中做了一次对雾霾知识了解程度的抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解。根据调查结果,绘制了如图所示的不完整的统计图。
结合统计图,回答下列问题:
(1)本次参与调查的学生一共有( )人。
(2)达到“基本了解”的同学占( )%。
(3)参与调查的学生中对雾霾情况“非常了解”的人数比“比较了解”的人数少( )%。
12.某工厂统计去年1~12月份生产总值。如果要反映各月产值的增减变化情况,可以绘制( )统计图;如果要反映每个月产值与全年总产值之间的关系,绘制( )统计图比较合适。
13.我国陆地领土总面积是960多万平方千米。如图是我国地形分布情况统计图,请根据统计图填空。
(1)我国平原面积占( )%。
(2)高原面积约有( )万平方千米。
(3)山地面积比盆地面积多( )万平方千米。
14.下图是六年一班同学为希望小学捐赠图书统计图,根据图示回答问题。
(1)捐赠的科技类图书占捐赠图书总数的( )%;
(2)如果捐赠的文学类图书有20本,则捐赠的科幻类图书有( )本。
三、判断题
15.从扇形统计图中可以看出各部分数量的多少。( )
16.扇形统计图中各部分百分比的和一定是100%。( )
17.要反映某小学本学期六年级数学月考成绩变化情况,应选择扇形统计图。( )
18.面粉中含有蛋白质、脂肪、糖类等营养物质,要表示各种成分的含量占总量的百分比的情况,应选择扇形统计图更合适。( )
19.要表示出六年级各班学生人数的情况,绘制折线统计图更直观。( )
四、计算题
20.一个数减少它的15%后是5.1,这个数是多少?(用方程解)
五、作图题
21.学校抽查了若干名小学生的坐姿、站姿、走姿的好坏情况(每个学生只记录最突出的一种),并将统计结果绘成如下两幅不完整的统计图。
(1)请将两幅统计图补充完整。
(2)一共抽查了_________人,其中站姿不良的学生人数比坐姿不良的学生人数少_________%。
(3)如该市共有学生14000人,则该市小学生中“三姿”良好的学生有_________人。
六、解答题
22.观察下面的统计图,先填空,再解答问题。
(1)这个统计图叫做( )统计图。我们可以用它来表示( )与( )之间的关系。
(2)如果用整个圆表示小红家每月总的支出是5000元,那么扇形B表示支出多少元?
23.六(2)班同学血型情况加图。该班有50人,O型血的人数占全班人数的百分之几?比A型血的人数多多少人?
24.如今,很多人都是“机不离手”。近日,某报社对中学生、大学生和上班族使用手机情况进行了一项抽样调查,聪聪根据调查结果绘制成如下不完整的统计图。
(1)结合统计图中的数据,可算出参与受访的一共有( )人;每天使用手机5小时以上的有( )人。
(2)将图中的条形统计图补充完整。
(3)每天使用手机5小时以上的占全部受访人数的( )%。
(4)88.5%的受访者坦言最近使用手机时长增加了,主要是刷短视频、网上购物和沟通工作。由于长时间观看手机屏幕会使眼睛疲劳、干涩,引发视力下降,所以养成良好的手机使用习惯很重要。对此,你有什么好的建议?(至少写出两条)
25.下图是实验一小六年级参加课后托管情况,他们分别参加体育、科技、音乐和其他四个类别的活动(每位同学只参加一项)。经过调查后,统计了他们参加四项活动的情况,并制成条形统计图和扇形统计图。
(1)请你根据图中数据,计算科技组的人数(填在方框中)。
(2)请在图中用条形表示音乐组的人数。
26.垃圾分类有利于改善城乡环境,保障人体健康,维护生态安全。垃圾的种类有可回收物,厨余垃圾,有害垃圾和其他垃圾。同学们对某小区一周产生的垃圾构成情况进行了调查,请你根据统计图完成下面的问题。
(1)这个小区这周一共产生垃圾多少吨?
(2)可回收垃圾有多少吨?请把条形统计图补充完整。
《六年级暑假新课预习提升练第七单元检测卷《扇形统计图》(含解析)-2024-2025学年下学期小学数学人教版》参考答案
题号 1 2 3 4 5 6 7
答案 A C C C C C B
1.A
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;
扇形统计图表示各部分数量与总数之间的关系。
【详解】妈妈想清楚地表示家里每月收入与各项消费的支出、储蓄理财等之间的关系,应该选用扇形统计图比较好。
故答案为:A
【点睛】理解掌握条形统计图、折线统计图、扇形统计图的特点是选择统计图的关键。
2.C
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此解答。
【详解】扇形统计图能清楚地表示部分数量与总数量之间的关系。
故答案为:C
3.C
【分析】先用加法求出总票数,再用小明、小亮、小红、小丽的得票数分别除以总票数再乘100%得出这四个人所占的百分比,从而判断出哪个扇形图是正确的,据此解答即可。
【详解】100+50+30+20
=150+30+20
=180+20
=200(票)
小明:100÷200×100%
=0.5×100%
=50%
小亮:50÷200×100%
=0.25×100%
=25%
小红:30÷200×100%
=0.15×100%
=15%
小丽:20÷200×100%
=0.1×100%
=10%
因此,选项C的图能准确表示这一结果。
故答案为:C
4.C
【分析】六月份有30天,晴天的天数占六月份天数的60%,根据求一个数的百分之几是多少,用乘法计算,即用30乘60%即可求解。
【详解】30×60%=18(天)
则本月的晴天有18天。
故答案为:C
5.C
【分析】根据扇形统计图的特点,用圆的面积表示全月总支出,圆周角是360°,教育支出占全月总支出的15%,也就是说教育支出的扇形圆心角占360°的15%,根据求一个数的百分之几是多少,用乘法计算,即可求出教育支出的扇形圆心角。
【详解】360°×15%
=360°×0.15
=54°
绘制她家上月支出情况的扇形统计图时画出教育支出的扇形圆心角应该是54°。
故答案为:C
【点睛】本题考查扇形统计图的特点及百分数乘法的应用,已知部分占总量的百分之几,也就是扇形的圆心角占360°的百分之几。
6.C
【分析】A.圆周率不会因为圆的大小而变化。
B.用4个半径相同,圆心角都是90°的扇形,能拼成一个圆。
C.根据圆形的面积=πr2,扇形的面积=πr2,扇形的大小与其半径的长短、圆心角的大小有关。
D.折线统计图特点是用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。要表示一个地区降水量的增减变化情况,用折线统计图表示最合适。
【详解】A.圆周率不因圆的大小而变化,所以原选项说法错误;
B.用4个半径相同,圆心角都是90°的扇形,才能拼成一个圆,所以原选项说法错误;
C.扇形的大小与其半径的长短、圆心角的大小有关,选项说法正确;
D.要表示一个地区降水量的增减变化情况,用折线统计图表示最合适,所以原选项说法错误。
故答案为:C
7.B
【分析】从条形统计图中可知,故事类图书有80本,科技类图书有40本,作文类图书有30本,漫画类图书有10本,一共有(80+40+30+10)本,用各类图书的本数除以总本数,求出各类图书占总本数的百分比,也就是各类图书的扇形面积占整个圆面积的百分比,结合各选项中的扇形统计图得出结论。
【详解】图书总数:80+40+30+10=160(本)
故事类图书占总本数的:80÷160×100%=50%
科技类图书占总本数的:40÷160×100%=25%
作文类图书占总本数的:30÷160×100%=18.75%
漫画类图书占总本数的:10÷160×100%=6.25%
50%>25%>18.75%>6.25%
A.图中第二大扇形的面积占整个圆的百分比>25%,不符合题意;
B.图中最大扇形的面积占整个圆的50%,第二大扇形的面积占整个圆的25%,剩下的两个小扇形也有大小区分,所以这个扇形统计图能准确表达这一统计结果;
C.图中最大扇形的面积占整个圆的百分比<50%,第二大扇形的面积占整个圆的百分比>25%,不符合题意;
D.图中两个小的扇形面积一样大,不符合题意。
故答案为:B
【点睛】理解掌握条形统计图、扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
8. 扇形 圆 扇形
【详解】扇形统计图可以清楚地反映出部分数量与总数之间的关系,它是用圆表示总数,用圆中的扇形表示部分所占总数的百分比。
如:我国陆地各种地形所占百分比:
9. 折线 条形
【分析】条形统计图可以直观地显示数量的多少。
折线统计图除了显示数量的多少,还可以清楚地反应数量的增减变化情况。
扇形统计图可以清楚地看出各部分数量和总数量之间的关系。
根据各种统计图的特点,选择合适的统计图,据此解答。
【详解】由分析得:
表现病人体温变化选用折线统计图;统计各科住院人数时选用条形统计图。
10.(1)三
(2)10
(3) 20 3
(4)50
【分析】(1)观察扇形统计图,哪个奖项所占的区域最大,那么获得这个奖项的人数就最多。
(2)把获奖总人数看作单位“1”,用“1”减去获得一等奖、二等奖、三等奖的人数分别占获奖总人数的百分比,即是获得优秀奖的人数占获奖总人数的百分之几。
(3)把获奖总人数看作单位“1”,已知获得优秀奖的有2人占获奖总人数的10%,单位“1”未知,用获得优秀奖的人数除以10%,即可求出获奖总人数;
从图中可知,获得一等奖的人数占获奖总人数的15%,根据求一个数的百分之几是多少,用获奖总人数乘15%,即是获得一等奖的人数。
(4)从图中可知,获得二等奖、三等奖的人数分别占获奖总人数的25%、50%,先用减法求出少的量,再除以获得三等奖占获奖总人数的百分比即可。
【详解】(1)获得三等奖的人数最多。
(2)1-15%-25%-50%=10%
获得优秀奖的人数占获奖总人数的10%。
(3)2÷10%
=2÷0.1
=20(人)
20×15%
=20×0.15
=3(人)
红旗小学获奖的一共20人,获得一等奖的有3人。
(4)(50%-25%)÷50%×100%
=(0.5-0.25)÷0.5×100%
=0.25÷0.5×100%
=0.5×100%
=50%
获得二等奖的人数比获得三等奖的人数少50%。
11.(1)400
(2)42
(3)87.5
【分析】(1)把调查的总人数看作单位“1”,不了解的有140人,占调查总人数的35%,根据已知一个数的百分之几是多少,求这个数,用除法解答;
(2)用比较了解的人数除以总人数,得出比较了解的人数占的百分率,再用减法计算即可得C部分基本了解占的百分率;
(3)用“比较了解”的人数减“非常了解”的人数,再除以“比较了解”的人数即可。
【详解】(1)140÷35%=400(人)
(2)80÷400×100%
=0.2×100%
=20%
1-3%-20%-35%
=97%-20%-35%
=77%-35%
=42%
(3)(80-10)÷80×100%
=70÷80×100%
=0.875×100%
=87.5%
【点睛】此题主要考查学生如何从扇形统计图、条形统计图中获取信息,然后再根据所获取的信息解决实际问题。
12. 折线 扇形
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】某工厂统计去年1~12月份生产总值。如果要反映各月产值的增减变化情况,可以绘制折线统计图;如果要反映每个月产值与全年总产值之间的关系,绘制扇形统计图比较合适。
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
13.(1)12
(2)249.6
(3)134.4
【分析】(1)把我国陆地总面积看作单位“1”,根据减法的意义,用1减去山地、盆地、丘陵、高原占总面积的百分率,即可解答。
(2)根据求一个数的百分之几是多少,用陆地领土总面积乘高原占总面积的百分率即可解答。
(3)先求出山地面积比盆地面积多占总面积的百分之几,然后根据求一个数的百分之几是多少,用乘法解答。
【详解】(1)1-33%-10%-26%-19%
=67%-10%-26%-19%
=57%-26%-19%
=31%-19%
=12%
我国平原面积占12%。
(2)960×26%=249.6(万平方千米)
高原面积约有249.6万平方千米。
(3)960×(33%-19%)
=960×14%
=134.4(万平方千米)
山地面积比盆地面积多134.4万平方千米。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
14.(1)25
(2)8
【分析】(1)从扇形统计图中可知,科技类图书的扇形的圆心角是90°,占整个圆的,化成小数是0.25,再化成百分数是25%,即可求解。
(2)把图书的总数看作单位“1”,从扇形统计图中可知,文学类图书的扇形占整个图的一半,即20本文学类图书占图书总数的50%,单位“1”未知,用文学类图书的本数除以50%,即可求出图书的总数;
图书的总数是单位“1”,用“1”减去科技类、文学类、童话类占总数的百分比之和,即是科幻类图书占总数的百分比;单位“1”已知,用图书总数乘科幻类图书的百分比,求出科幻类图书的本数。
【详解】(1)=0.25=25%
捐赠的科技类图书占捐赠图书总数的25%。
(2)图书的总数:
20÷50%
=20÷0.5
=40(本)
科幻类图书占图书总数的:
1-(25%+50%+5%)
=1-80%
=20%
科幻类图书有:
40×20%
=40×0.2
=8(本)
【点睛】本题考查百分数的应用,根据扇形统计图提供的信息,解决有关的百分数问题。明确已知一个数的百分之几是多少,求这个数,用除法计算;求一个数的百分之几是多少,用乘法计算。
15.×
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;
扇形统计图表示各部分数量与总数之间的关系或各部分与各部分之间的关系。
【详解】从扇形统计图中可以看出各部分数量与总数之间的关系。
原题说法错误。
故答案为:×
【点睛】本题考查扇形统计图的特点。
16.√
【分析】在扇形统计图中,整个圆代表总体,把总体看作单位“1”,每个扇形代表总体中的各部分,各部分之和等于单位“1”,即各部分数量占总数的百分比的总和都是100%。
【详解】分析可知,任何扇形统计图中,各部分数量占总数的百分比的总和都是100%。
故答案为:√
【点睛】扇形统计图是用圆的面积表示总数,用圆内扇形的面积表示各部分占总数的百分比。
17.×
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况解答即可。
【详解】要反映某小学本学期六年级数学月考成绩变化情况,应选择折线统计图。
故答案为:×
【点睛】此题根据扇形统计图、折线统计图、条形统计图各自的特点来判断。
18.√
【分析】扇形统计图是以一个圆的面积(看作单位“1”)表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数的统计图。
【详解】面粉中含有蛋白质、脂肪、糖类等营养物质,要表示各种成分的含量占总量的百分比的情况,应选择扇形统计图更合适,说法正确。
故答案为:√
【点睛】扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系。
19.×
【分析】条形统计图的特点是能清楚地表示出各种数量的多少;折线统计图的特点是既能表示出各种数量的多少,又能表示出数量的增减变化情况;扇形统计图的特点是能从图中清楚地看出各部分数量占总数的百分比,以及部分与部分之间的关系。根据要反映的信息,结合三种统计图的特点选择统计图。
【详解】根据三种统计图的特点,要表示出六年级各班学生人数的情况,绘制条形统计图更直观。
故答案为:×
【点睛】区别不同统计图的应用范围是解决此题的关键。
20.6
【分析】求一个数的百分之几是多少用乘法,设这个数是x,根据这个数-这个数×15%=5.1,列出方程求出x的值即可。
【详解】解:设这个数是x。
x-15%x=5.1
0.85x=5.1
0.85x÷0.85=5.1÷0.85
x=6
这个数是6。
21.(1)见详解
(2)500;40
(3)4200
【分析】(1)把学校抽查的若干名小学生的人数看作单位“1”,用1减去坐姿、站姿、走姿不良的人数占被抽查的百分率,就是三姿良好的人数占的百分率,据此补充扇形统计图;已知一个数的百分之几是多少,求这个数用除法,由条形统计图可知,坐姿不良的人数是100,由扇形统计图可知,坐姿不良的人数占单位“1”的20%,用100÷20%列式求出学校抽查的若干名小学生的人数,根据求一个数的百分之几是多少,用乘法,用学校抽查的若干名小学生的人数乘三姿良好的人数占的百分率,求出三姿良好的人数,据此补充条形统计图;
(2)由(1)可知一共抽查的人数;求一个数比另一个数少百分之几,用两个数的差除以另一个数,据此用坐姿不良的学生人数占抽查人数的百分率减去坐姿不良的学生人数占抽查人数的百分率,再除以坐姿不良的学生人数占抽查人数的百分率即可解答;
(3)把该市共有学生的总人数看作单位“1”,求一个数的百分之几是多少,用乘法解答,用14000乘三姿”良好的学生占的百分率即可解答。
【详解】(1)1-20%-12%-38%
=80%-12%-38%
=68%-38%
=30%
100÷20%=500(人)
500×30%=150(人)
如图:
(2)由(1)可知:一共抽查了500人;
(20%-12%)÷20%
=0.08÷0.2
=40%
所以一共抽查了500人,其中站姿不良的学生人数比坐姿不良的学生人数少40%。
(3)14000×30%=4200(人)
所以该市小学生中“三姿”良好的学生有4200人。
22.(1)扇形;部分;整体;(2)1500元
【分析】(1)扇形统计图是以一个圆的面积(看作单位“1”)表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数的统计图。
(2)把小红家每月总支出看作单位“1”,用1减去A项、C项的支出占总支出的百分比,即可求出扇形B占总支出的百分比,求一个数的百分之几是多少,用乘法,用小红家每月总支出5000元乘扇形B占总支出的百分比,即可求出扇形B支出多少元。
【详解】(1)这个统计图叫做扇形统计图。我们可以用它来表示部分与整体之间的关系。
(2)5000×(1-45%-25%)
=5000×(1-0.45-0.25)
=5000×0.3
=1500(元)
答:扇形B表示支出1500元。
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
23.40%;6人
【分析】把该班总人数看作单位“1”,用减法计算即可得O型血的人数占全班人数的百分之几;用该班的总人数分别乘O型血的人数和A型血的人数占总人数的百分率,再相减即可。
【详解】1-24%-28%-8%
=76%-28%-8%
=40%
50×40%-50×28%
=20-14
=6(人)
答:O型血的人数占全班人数的40%,O型血的人数比A型血的人数多6人。
【点睛】此题主要考查的是如何从扇形统计图中获取信息,然后再根据信息进行计算的能力。
24.(1)2000;900
(2)见详解
(3)45
(4)见详解
【分析】(1)观察可知,把参与受访总人数看作单位“1”,已知1-3小时有360人占总人数的18%,根据已知一个数的百分之几是多少,求这个数用除法计算,可得参与受访总人数;用总人数减去其它三个时间段的人数可得5小时以上的人数。
(2)观察可知条形统计图的横轴表示时长,纵轴表示人数,纵轴每格表示100人,据此画出表示5小时以上的人数的直条即可。
(3)根据求一个数占另一个数的百分之几,用除法计算,用每天使用手机5小时以上的除以全部受访人数。
(4)由题可知:过渡使用手机是造成视力问题的主要原因,所以建议从合理控制使用手机时长,多做户外运动等方面提出即可。
【详解】(1)(人)
(人)
结合统计图中的数据,可算出参与受访的一共有2000人;每天使用手机5小时以上的有900人。
(2)如下图:
(3)
每天使用手机5小时以上的占全部受访人数的45%。
(4)答:1.减少手机的使用时间,用眼一段时间后做眼保健操放松眼睛,避免用眼过渡;2.多参加户外运动。(答案唯一)
25.(1)30人
(2)见详解
【分析】(1)将总人数看作“1”,体育组人数÷对应百分率=总人数,总人数×科技组对应百分率=科技组人数。
(2)1-体育组对应百分率-科技组对应百分率-其他组对应百分率=音乐组对应百分率,总人数×音乐组对应百分率=音乐组人数,据此补充条形统计图。
【详解】(1)48÷40%×25%
=48÷0.4×0.25
=30(人)
(2)48÷40%×(1-40%-25%-15%)
=48÷0.4×0.2
=24(人)
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
26.(1)40吨;(2)10吨;见详解。
【分析】(1)厨余垃圾是22吨,厨余垃圾占这周垃圾总吨数的55%,已知一个数的百分之几是多少,求这个数,用除法,列式:22÷55%,即可求出这个小区这周一共产生的垃圾总吨数。
(2)把这周垃圾总吨数看作单位“1”,用1连续减去厨余垃圾、有害垃圾和其他垃圾占垃圾总吨数的百分比,即可求得可回收物占这周垃圾总吨数的百分比,再用这周垃圾总吨数乘可回收物占这周垃圾总吨数的百分比,即可求出可回收垃圾的吨数。并把数据补充到条形统计图中。
【详解】(1)22÷55%=40(吨)
答:这个小区这周一共产生垃圾40吨。
(2)1-16%-4%-55%=25%
40×25%=10(吨)
答:可回收垃圾有10吨。
补充如下:
【点睛】此题考查的目的是理解掌握条形统计图和扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
