5.2.3 解方程(1)(分层作业)(含答案)2025-2026学年人教版数学五年级上册
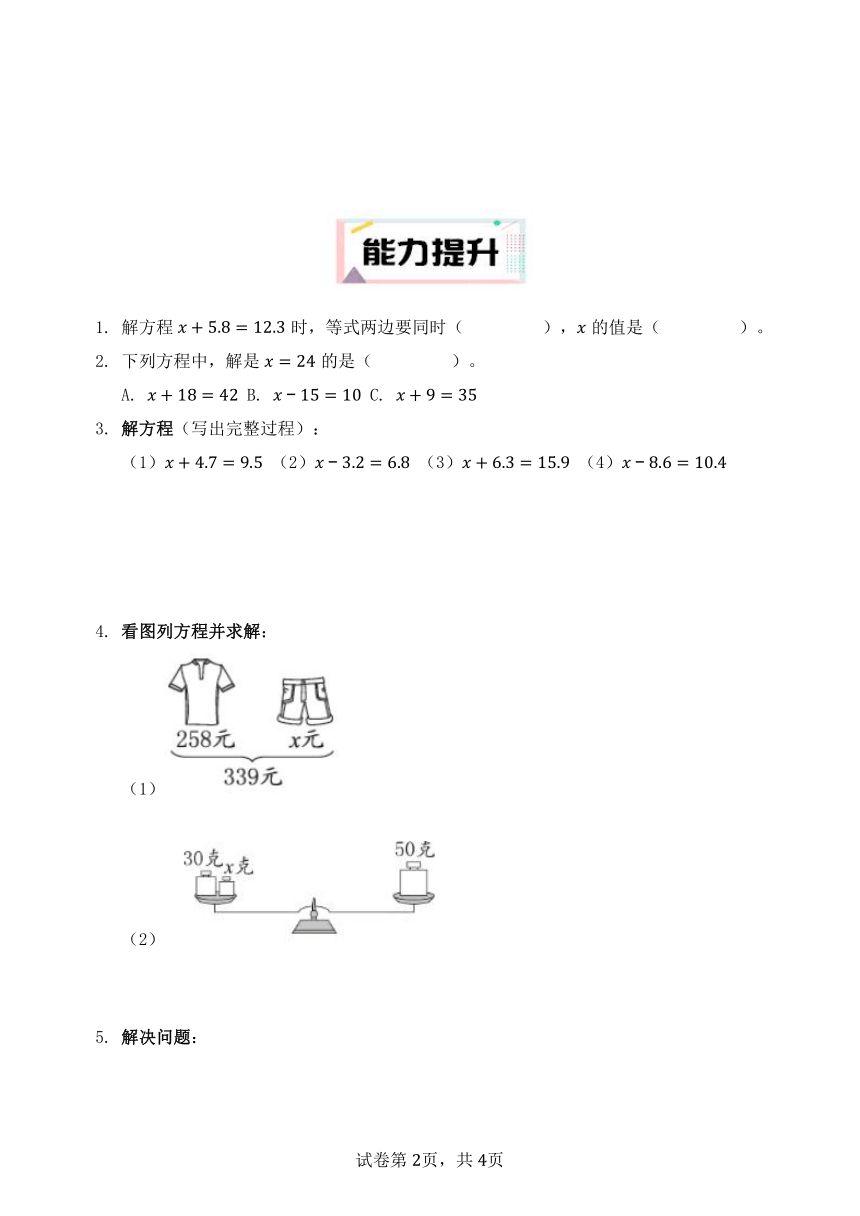
文档属性
| 名称 | 5.2.3 解方程(1)(分层作业)(含答案)2025-2026学年人教版数学五年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 79.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-28 08:45:52 | ||
图片预览


文档简介
5.2.3 解方程(1)(分层作业)
2025-2026学年人教版数学五年级上册
( )叫做方程的解;( )叫做解方程。
方程的解是( )。
A. B. C.
解方程(写出完整过程):
(1) (2) (3) (4)
连线题:把方程和对应的解连起来。
根据文字列方程:
(1)一个数加上15等于42,设这个数为,列方程为( )。
(2)一个数减去9等于23,设这个数为,列方程为( )。
(3)比多7的数是30,列方程为( )。
解决问题:
(1)商店运来一批水果,卖出28千克后,还剩52千克。设这批水果原来有千克,列方程并求解。
(2)一根铁丝,用去15米后,还剩35米。设这根铁丝原来长米,列方程并求解。
解方程时,等式两边要同时( ),的值是( )。
下列方程中,解是的是( )。
A. B. C.
解方程(写出完整过程):
(1) (2) (3) (4)
看图列方程并求解:
(1)
(2)
解决问题:
(1)一个篮球的价格比一个皮球贵35元,已知皮球价格是25元,设篮球价格是元,列方程并求解。
(2)一张桌子的价格比一把椅子贵60元,已知桌子价格是150元,设椅子价格是元,列方程并求解。
(3)一只鸭的重量比一只鸡重1.2千克,已知鸡重2.5千克,设鸭重千克,列方程并求解。
根据解写方程:写出两个解是的方程:( )、( )。
求未知数:在x+□中,当时,□里的数是多少?当□=12时,的值是多少?
编题:编一道可以用方程解决的实际问题。
和差关系问题:甲、乙两数的和是94,甲数比乙数大8。设乙数为,列方程求出甲、乙两数分别是多少。
倍数与移多补少问题:一个两层书架,上层书的本数是下层的2倍。如果从上层拿15本到下层,两层书的本数就同样多。设下层原来有本书,列方程求出上、下层原来各有多少本书。
试卷第1页,共3页
试卷第2页,共2页
答案与解析
基础巩固
使方程左右两边相等的未知数的值;求方程的解的过程
解析:考查方程的解与解方程的定义,直接依据概念填空。
B
解析:解方程时,根据等式性质1,两边同时加13,得,故选B。
(1)解:,
(2)解:,
(3)解:,
(4)解:,
解析:均根据等式性质1,等式两边同时加或减同一个数求解,注意书写格式。
连;连;连;连
解析:分别解方程得解后连线,如的解为。
(1) (2) (3)
解析:根据文字描述的数量关系直接列方程,(3)中“比多7”即。
(1)解:列方程,根据等式性质1,两边加28得
(2)解:列方程,两边加15得
解析:均依据“原有数量 - 用去数量 = 剩余数量”列方程,再用等式性质求解。
能力提升
减5.8;6.5
解析:解方程时,根据等式性质1,两边同时减5.8,得。
A
解析:将代入选项验证,A选项成立,故选A。
(1)解:,
(2)解:,
(3)解:,
(4)解:,
解析:针对含小数的方程,用等式性质1求解,注意小数加减法的计算准确性。
(1)解:【答案】
258+x=339
解:258+x-258=339-258
x=81
(2)【答案】30+z=50
解:x=50-30
x=20
(1)解:列方程,两边加25得
(2)解:列方程(或),解得
(3)解:列方程,两边加2.5得
解析:均围绕“较大数 - 较小数 = 相差数”列方程,体现两数的差量关系。
示例:;(答案不唯一)
解析:根据解,构造含的加法或减法方程,确保等式成立。
当时,□;当□时,
解析:根据加法各部分关系“一个加数 = 和 - 另一个加数”计算。
示例:妈妈买了一些苹果,又买了32个后,现在共有67个,妈妈原来买了多少个苹果?(答案不唯一)
解析:围绕“原有数量 + 增加数量 = 现有数量”的关系编题,符合方程的含义。
思维拓展
解:甲数为,列方程,化简得,两边减8得,解得,甲数为
解析:通过设乙数为,用含的式子表示甲数,再根据两数和为94列方程,体现和差问题的建模思路。
解:上层原有本,列方程,两边减得,两边加15得,上层有本
解析:根据“移动后两层本数相等”的等量关系列方程,体现移多补少中数量的平衡关系,需理解倍数与差量的转化。
2025-2026学年人教版数学五年级上册
( )叫做方程的解;( )叫做解方程。
方程的解是( )。
A. B. C.
解方程(写出完整过程):
(1) (2) (3) (4)
连线题:把方程和对应的解连起来。
根据文字列方程:
(1)一个数加上15等于42,设这个数为,列方程为( )。
(2)一个数减去9等于23,设这个数为,列方程为( )。
(3)比多7的数是30,列方程为( )。
解决问题:
(1)商店运来一批水果,卖出28千克后,还剩52千克。设这批水果原来有千克,列方程并求解。
(2)一根铁丝,用去15米后,还剩35米。设这根铁丝原来长米,列方程并求解。
解方程时,等式两边要同时( ),的值是( )。
下列方程中,解是的是( )。
A. B. C.
解方程(写出完整过程):
(1) (2) (3) (4)
看图列方程并求解:
(1)
(2)
解决问题:
(1)一个篮球的价格比一个皮球贵35元,已知皮球价格是25元,设篮球价格是元,列方程并求解。
(2)一张桌子的价格比一把椅子贵60元,已知桌子价格是150元,设椅子价格是元,列方程并求解。
(3)一只鸭的重量比一只鸡重1.2千克,已知鸡重2.5千克,设鸭重千克,列方程并求解。
根据解写方程:写出两个解是的方程:( )、( )。
求未知数:在x+□中,当时,□里的数是多少?当□=12时,的值是多少?
编题:编一道可以用方程解决的实际问题。
和差关系问题:甲、乙两数的和是94,甲数比乙数大8。设乙数为,列方程求出甲、乙两数分别是多少。
倍数与移多补少问题:一个两层书架,上层书的本数是下层的2倍。如果从上层拿15本到下层,两层书的本数就同样多。设下层原来有本书,列方程求出上、下层原来各有多少本书。
试卷第1页,共3页
试卷第2页,共2页
答案与解析
基础巩固
使方程左右两边相等的未知数的值;求方程的解的过程
解析:考查方程的解与解方程的定义,直接依据概念填空。
B
解析:解方程时,根据等式性质1,两边同时加13,得,故选B。
(1)解:,
(2)解:,
(3)解:,
(4)解:,
解析:均根据等式性质1,等式两边同时加或减同一个数求解,注意书写格式。
连;连;连;连
解析:分别解方程得解后连线,如的解为。
(1) (2) (3)
解析:根据文字描述的数量关系直接列方程,(3)中“比多7”即。
(1)解:列方程,根据等式性质1,两边加28得
(2)解:列方程,两边加15得
解析:均依据“原有数量 - 用去数量 = 剩余数量”列方程,再用等式性质求解。
能力提升
减5.8;6.5
解析:解方程时,根据等式性质1,两边同时减5.8,得。
A
解析:将代入选项验证,A选项成立,故选A。
(1)解:,
(2)解:,
(3)解:,
(4)解:,
解析:针对含小数的方程,用等式性质1求解,注意小数加减法的计算准确性。
(1)解:【答案】
258+x=339
解:258+x-258=339-258
x=81
(2)【答案】30+z=50
解:x=50-30
x=20
(1)解:列方程,两边加25得
(2)解:列方程(或),解得
(3)解:列方程,两边加2.5得
解析:均围绕“较大数 - 较小数 = 相差数”列方程,体现两数的差量关系。
示例:;(答案不唯一)
解析:根据解,构造含的加法或减法方程,确保等式成立。
当时,□;当□时,
解析:根据加法各部分关系“一个加数 = 和 - 另一个加数”计算。
示例:妈妈买了一些苹果,又买了32个后,现在共有67个,妈妈原来买了多少个苹果?(答案不唯一)
解析:围绕“原有数量 + 增加数量 = 现有数量”的关系编题,符合方程的含义。
思维拓展
解:甲数为,列方程,化简得,两边减8得,解得,甲数为
解析:通过设乙数为,用含的式子表示甲数,再根据两数和为94列方程,体现和差问题的建模思路。
解:上层原有本,列方程,两边减得,两边加15得,上层有本
解析:根据“移动后两层本数相等”的等量关系列方程,体现移多补少中数量的平衡关系,需理解倍数与差量的转化。
