3.7 二元一次方程组的应用 同步练习(含答案)
文档属性
| 名称 | 3.7 二元一次方程组的应用 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 497.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-28 17:13:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.7 二元一次方程组的应用
一、单选题
1.“悟空顺风探妖踪,千里只用五分钟;归时五分行六百,试问风速是多少?”大致意思是:孙悟空追寻妖精的行踪,去时顺风,1000里只用了5分钟:回来时逆风,5分钟只走了600里,试求风的速度是每分钟多少里?( )
A.30 B.40 C.50 D.60
2.《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问:甲、乙持钱各几何?”大意是:甲、乙二人带着钱,不知是多少,若甲得到乙的钱数的,则甲的钱数为50,若乙得到甲的钱数的,则乙的钱数也能为50.问甲、乙各有多少钱?设甲有钱为x,乙有钱为y,可列方程组为( )
A. B.
C. D.
3.(2019七下·商南期末)用四个完全一样的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是121,小正方形的面积是9,若用 表示长方形的长和宽,则下列关系式中不正确的是( )
A. B. C. D.
4.(2019七下·卫辉期中)七年级学生在会议室开会,每排座位坐12人,则有11人没有座位;每排座位坐14人,则余1人独坐一排,则这间会议室的座位排数是( )
A.14 B.13 C.12 D.15
5.在《九章算术》中,二元一次方程组是通过“算筹”摆放的,如图1、图2所示.图中各行从左到右列出的算筹数分别表示未知数,的系数与相应的常数项.如图1所示的算筹图表示的方程组是,类似的,图2所示的算筹图表示的方程组是( )
A. B.
C. D.
6.一个两位数的十位数字与个位数字之和是7,如果把这个两位数加上45,那么恰好成为把个位数字和十位数字对调后组成的数,那么这个两位数是( )
A.16 B.25 C.52 D.61
7.(2019七下·黄陂期末)《九章算术》中有个方程问题:“五只雀、六只燕,共重1斤(等于16两),雀重燕轻.互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?”设每只雀重 两,每只燕重 两,依题意列方程组( )
A. B.
C. D.
8.(2019七下·大庆期中)我国古代数学著作《增删算法统宗》记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则正确方程组是( )
A. B.
C. D.
9.(2022九下·渝北期中)我国古代数学著作《增删算法统宗》中有这么一首诗:“今有布绢三十疋,共卖价钞五百七.四疋绢价九十贯,三疋布价该五十.欲问绢布各几何?价钞各该分端的.若人算得无差讹,堪把芳名题郡邑.”其大意是:今有绵与布30疋,卖得570贯钱,4疋绢价90贯,3疋布价50贯,欲问绢布有多少,分开把价算,若人算得无差错,你的名字城镇到处扬.设有绢 疋,布 疋,依据题意可列方程组为( )
A. B.
C. D.
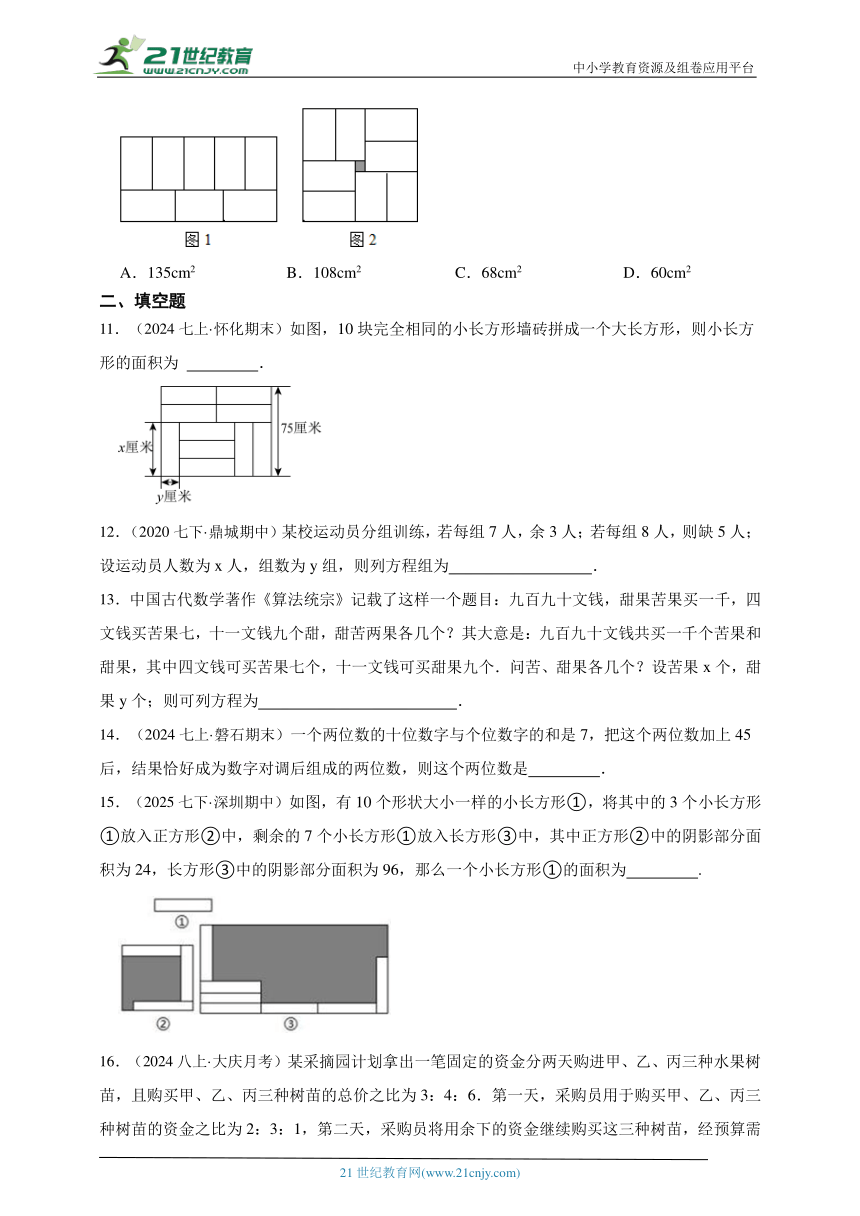
10.(2020七下·沂水期末)小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图1;小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图2那样的正方形,中间还留下了一个洞,恰好是面积为 的小正方形,则每个小长方形的面积为( )
A.135cm2 B.108cm2 C.68cm2 D.60cm2
二、填空题
11.(2024七上·怀化期末)如图,10块完全相同的小长方形墙砖拼成一个大长方形,则小长方形的面积为 .
12.(2020七下·鼎城期中)某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为 .
13.中国古代数学著作《算法统宗》记载了这样一个题目:九百九十文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:九百九十文钱共买一千个苦果和甜果,其中四文钱可买苦果七个,十一文钱可买甜果九个.问苦、甜果各几个?设苦果x个,甜果y个;则可列方程为 .
14.(2024七上·磐石期末)一个两位数的十位数字与个位数字的和是7,把这个两位数加上45后,结果恰好成为数字对调后组成的两位数,则这个两位数是 .
15.(2025七下·深圳期中)如图,有10个形状大小一样的小长方形①,将其中的3个小长方形①放入正方形②中,剩余的7个小长方形①放入长方形③中,其中正方形②中的阴影部分面积为24,长方形③中的阴影部分面积为96,那么一个小长方形①的面积为 .
16.(2024八上·大庆月考)某采摘园计划拿出一笔固定的资金分两天购进甲、乙、丙三种水果树苗,且购买甲、乙、丙三种树苗的总价之比为3:4:6.第一天,采购员用于购买甲、乙、丙三种树苗的资金之比为2:3:1,第二天,采购员将用余下的资金继续购买这三种树苗,经预算需将余下资金的购买甲树苗,则采购员还需购买的乙、丙树苗的资金之比为 .
三、计算题
17.某班班主任打算购买一些学习用品以对本学期学习有进步的同学进行奖励.班主任委托班长购买奖品,下面是班长买回奖品时与班主任的对话情境.
(1)试计算两种笔记本各买了多少本?
(2)班长购买奖品为什么不可能找回68元?
18.小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60米,下坡路每分钟走80米,上坡路每分钟走40米,则他从家里到学校需10分钟,从学校到家里需15分钟.
(1)小华家离学校多远?
(2)小华从家里到学校到达中点的时间与小华从学校到家里到达中点的时间会一样吗?如果不一样,哪种情况所花的时间更多?请通过计算说明理由.
19.“利海”通讯器材商场,计划用60000元从厂家购进若干部新型手机,出厂价分别为甲种型号手机每部1800元,乙种型号手机每部600元,丙种型号手机每部1200元.若商场同时购进其中两种不同型号的手机共40部,并将60000元恰好用完,请你帮助商场计算一下如何购买.
四、解答题
20.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应如何分配工人才能使螺栓和螺帽刚好配套?
21.(我国古代算题)马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两,问马、牛各价几何
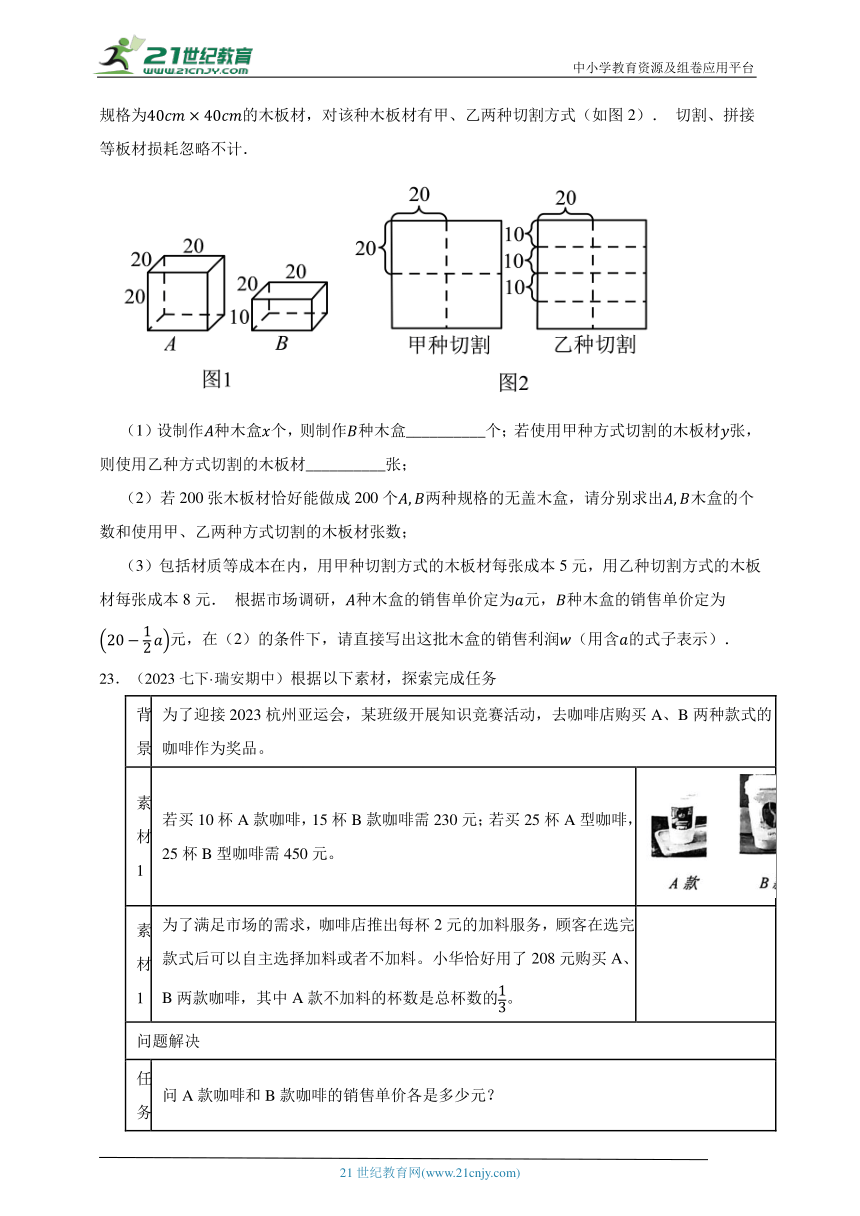
22.要制作200个两种规格的顶部无盖木盒,种规格是长、宽、高都为的正方体无盖木盒,种规格是长、宽、高各为的长方体无盖木盒(如图1);现有200张规格为的木板材,对该种木板材有甲、乙两种切割方式(如图2). 切割、拼接等板材损耗忽略不计.
(1)设制作种木盒个,则制作种木盒__________个;若使用甲种方式切割的木板材张,则使用乙种方式切割的木板材__________张;
(2)若200张木板材恰好能做成200个两种规格的无盖木盒,请分别求出木盒的个数和使用甲、乙两种方式切割的木板材张数;
(3)包括材质等成本在内,用甲种切割方式的木板材每张成本5元,用乙种切割方式的木板材每张成本8元. 根据市场调研,种木盒的销售单价定为元,种木盒的销售单价定为元,在(2)的条件下,请直接写出这批木盒的销售利润(用含的式子表示).
23.(2023七下·瑞安期中)根据以下素材,探索完成任务
背景 为了迎接2023杭州亚运会,某班级开展知识竞赛活动,去咖啡店购买A、B两种款式的咖啡作为奖品。
素材1 若买10杯A款咖啡,15杯B款咖啡需230元;若买25杯A型咖啡,25杯B型咖啡需450元。
素材1 为了满足市场的需求,咖啡店推出每杯2元的加料服务,顾客在选完款式后可以自主选择加料或者不加料。小华恰好用了208元购买A、B两款咖啡,其中A款不加料的杯数是总杯数的。
问题解决
任务1 问A款咖啡和B款咖啡的销售单价各是多少元?
任务2 在不加料的情况下,购买A、B两种款式的咖啡( 两种都要),刚好花200元,问有几种购买方案?
任务3 求小华购买的这两款咖啡,其中B型加料的咖啡买了多少杯(直接写出答案)?
答案解析部分
1.【答案】B
【知识点】二元一次方程组的实际应用-行程问题
2.【答案】B
【知识点】二元一次方程组的应用-古代数学问题
3.【答案】B
【知识点】二元一次方程组的应用-几何问题
4.【答案】C
【知识点】二元一次方程组的其他应用
5.【答案】B
【知识点】二元一次方程组的应用-古代数学问题
6.【答案】A
【知识点】二元一次方程组的应用-数字问题
7.【答案】A
【知识点】二元一次方程组的应用-古代数学问题
8.【答案】A
【知识点】二元一次方程组的应用-古代数学问题
9.【答案】B
【知识点】二元一次方程组的应用-古代数学问题
10.【答案】A
【知识点】二元一次方程组的应用-几何问题
11.【答案】675
【知识点】二元一次方程组的应用-几何问题
12.【答案】
【知识点】二元一次方程组的其他应用
13.【答案】
【知识点】二元一次方程组的应用-古代数学问题
14.【答案】16
【知识点】二元一次方程组的应用-数字问题
15.【答案】5
【知识点】二元一次方程组的应用-几何问题
16.【答案】5:11
【知识点】二元一次方程组的实际应用-配套问题
17.【答案】(1)元、元的笔记本分别买了本和本
(2)不可能
【知识点】一元一次方程的其他应用;二元一次方程组的实际应用-销售问题
18.【答案】(1)小华家离学校700米
(2)小华从学校到家里到达中点的时间比小华从家里到学校到达中点的时间要多一些
【知识点】有理数混合运算的实际应用;二元一次方程组的实际应用-行程问题
19.【答案】两种购买方法:甲种型号手机购买30部,乙种型号手机购买10部;或甲种型号手机购买20部,丙种型号手机购买20部
【知识点】二元一次方程组的实际应用-方案选择题问题
20.【答案】分配40名工人生产螺栓,50名工人生产螺帽.
【知识点】二元一次方程组的实际应用-配套问题
21.【答案】解:设一匹马价x两,一头牛价y两,
由题意得:
解得:
答:一匹马价6两,一头牛价4两
【知识点】二元一次方程组的应用-古代数学问题
22.【答案】(1),
(2)故制作种木盒100个,制作种木盒100个,使用甲种方式切割的木板150张,使用乙种方式切割的木板材50张.
(3)
【知识点】二元一次方程组的其他应用
23.【答案】解:任务1:设A型咖啡的每杯价格为x元,B型咖啡每杯价格为y元
由题可知:
解得;
答:A型咖啡的每杯价格为8元,B型咖啡每杯价格为10元;
任务2:设A型咖啡为m:杯 ,B型咖啡为n杯
则8m+10n=200
解得:,,, ,
∴共有四种方案;
任务3:买了6杯,理由如下:
设A型不加料为a杯 ,总的杯数为3a杯,设A型的加料和B型的不加料为b杯,则B型的加料为(2a-b)杯,
∴8a+10b+12(2a-b)=208
∴
因为a是整数
所以b=8,a=7
b=24 ,a=89不合题意
所以2a-b=2×7-8=6 ,即B型加料的咖啡买了6杯.
【知识点】二元一次方程的应用;二元一次方程组的实际应用-销售问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.7 二元一次方程组的应用
一、单选题
1.“悟空顺风探妖踪,千里只用五分钟;归时五分行六百,试问风速是多少?”大致意思是:孙悟空追寻妖精的行踪,去时顺风,1000里只用了5分钟:回来时逆风,5分钟只走了600里,试求风的速度是每分钟多少里?( )
A.30 B.40 C.50 D.60
2.《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问:甲、乙持钱各几何?”大意是:甲、乙二人带着钱,不知是多少,若甲得到乙的钱数的,则甲的钱数为50,若乙得到甲的钱数的,则乙的钱数也能为50.问甲、乙各有多少钱?设甲有钱为x,乙有钱为y,可列方程组为( )
A. B.
C. D.
3.(2019七下·商南期末)用四个完全一样的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是121,小正方形的面积是9,若用 表示长方形的长和宽,则下列关系式中不正确的是( )
A. B. C. D.
4.(2019七下·卫辉期中)七年级学生在会议室开会,每排座位坐12人,则有11人没有座位;每排座位坐14人,则余1人独坐一排,则这间会议室的座位排数是( )
A.14 B.13 C.12 D.15
5.在《九章算术》中,二元一次方程组是通过“算筹”摆放的,如图1、图2所示.图中各行从左到右列出的算筹数分别表示未知数,的系数与相应的常数项.如图1所示的算筹图表示的方程组是,类似的,图2所示的算筹图表示的方程组是( )
A. B.
C. D.
6.一个两位数的十位数字与个位数字之和是7,如果把这个两位数加上45,那么恰好成为把个位数字和十位数字对调后组成的数,那么这个两位数是( )
A.16 B.25 C.52 D.61
7.(2019七下·黄陂期末)《九章算术》中有个方程问题:“五只雀、六只燕,共重1斤(等于16两),雀重燕轻.互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?”设每只雀重 两,每只燕重 两,依题意列方程组( )
A. B.
C. D.
8.(2019七下·大庆期中)我国古代数学著作《增删算法统宗》记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则正确方程组是( )
A. B.
C. D.
9.(2022九下·渝北期中)我国古代数学著作《增删算法统宗》中有这么一首诗:“今有布绢三十疋,共卖价钞五百七.四疋绢价九十贯,三疋布价该五十.欲问绢布各几何?价钞各该分端的.若人算得无差讹,堪把芳名题郡邑.”其大意是:今有绵与布30疋,卖得570贯钱,4疋绢价90贯,3疋布价50贯,欲问绢布有多少,分开把价算,若人算得无差错,你的名字城镇到处扬.设有绢 疋,布 疋,依据题意可列方程组为( )
A. B.
C. D.
10.(2020七下·沂水期末)小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图1;小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图2那样的正方形,中间还留下了一个洞,恰好是面积为 的小正方形,则每个小长方形的面积为( )
A.135cm2 B.108cm2 C.68cm2 D.60cm2
二、填空题
11.(2024七上·怀化期末)如图,10块完全相同的小长方形墙砖拼成一个大长方形,则小长方形的面积为 .
12.(2020七下·鼎城期中)某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为 .
13.中国古代数学著作《算法统宗》记载了这样一个题目:九百九十文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:九百九十文钱共买一千个苦果和甜果,其中四文钱可买苦果七个,十一文钱可买甜果九个.问苦、甜果各几个?设苦果x个,甜果y个;则可列方程为 .
14.(2024七上·磐石期末)一个两位数的十位数字与个位数字的和是7,把这个两位数加上45后,结果恰好成为数字对调后组成的两位数,则这个两位数是 .
15.(2025七下·深圳期中)如图,有10个形状大小一样的小长方形①,将其中的3个小长方形①放入正方形②中,剩余的7个小长方形①放入长方形③中,其中正方形②中的阴影部分面积为24,长方形③中的阴影部分面积为96,那么一个小长方形①的面积为 .
16.(2024八上·大庆月考)某采摘园计划拿出一笔固定的资金分两天购进甲、乙、丙三种水果树苗,且购买甲、乙、丙三种树苗的总价之比为3:4:6.第一天,采购员用于购买甲、乙、丙三种树苗的资金之比为2:3:1,第二天,采购员将用余下的资金继续购买这三种树苗,经预算需将余下资金的购买甲树苗,则采购员还需购买的乙、丙树苗的资金之比为 .
三、计算题
17.某班班主任打算购买一些学习用品以对本学期学习有进步的同学进行奖励.班主任委托班长购买奖品,下面是班长买回奖品时与班主任的对话情境.
(1)试计算两种笔记本各买了多少本?
(2)班长购买奖品为什么不可能找回68元?
18.小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60米,下坡路每分钟走80米,上坡路每分钟走40米,则他从家里到学校需10分钟,从学校到家里需15分钟.
(1)小华家离学校多远?
(2)小华从家里到学校到达中点的时间与小华从学校到家里到达中点的时间会一样吗?如果不一样,哪种情况所花的时间更多?请通过计算说明理由.
19.“利海”通讯器材商场,计划用60000元从厂家购进若干部新型手机,出厂价分别为甲种型号手机每部1800元,乙种型号手机每部600元,丙种型号手机每部1200元.若商场同时购进其中两种不同型号的手机共40部,并将60000元恰好用完,请你帮助商场计算一下如何购买.
四、解答题
20.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应如何分配工人才能使螺栓和螺帽刚好配套?
21.(我国古代算题)马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两,问马、牛各价几何
22.要制作200个两种规格的顶部无盖木盒,种规格是长、宽、高都为的正方体无盖木盒,种规格是长、宽、高各为的长方体无盖木盒(如图1);现有200张规格为的木板材,对该种木板材有甲、乙两种切割方式(如图2). 切割、拼接等板材损耗忽略不计.
(1)设制作种木盒个,则制作种木盒__________个;若使用甲种方式切割的木板材张,则使用乙种方式切割的木板材__________张;
(2)若200张木板材恰好能做成200个两种规格的无盖木盒,请分别求出木盒的个数和使用甲、乙两种方式切割的木板材张数;
(3)包括材质等成本在内,用甲种切割方式的木板材每张成本5元,用乙种切割方式的木板材每张成本8元. 根据市场调研,种木盒的销售单价定为元,种木盒的销售单价定为元,在(2)的条件下,请直接写出这批木盒的销售利润(用含的式子表示).
23.(2023七下·瑞安期中)根据以下素材,探索完成任务
背景 为了迎接2023杭州亚运会,某班级开展知识竞赛活动,去咖啡店购买A、B两种款式的咖啡作为奖品。
素材1 若买10杯A款咖啡,15杯B款咖啡需230元;若买25杯A型咖啡,25杯B型咖啡需450元。
素材1 为了满足市场的需求,咖啡店推出每杯2元的加料服务,顾客在选完款式后可以自主选择加料或者不加料。小华恰好用了208元购买A、B两款咖啡,其中A款不加料的杯数是总杯数的。
问题解决
任务1 问A款咖啡和B款咖啡的销售单价各是多少元?
任务2 在不加料的情况下,购买A、B两种款式的咖啡( 两种都要),刚好花200元,问有几种购买方案?
任务3 求小华购买的这两款咖啡,其中B型加料的咖啡买了多少杯(直接写出答案)?
答案解析部分
1.【答案】B
【知识点】二元一次方程组的实际应用-行程问题
2.【答案】B
【知识点】二元一次方程组的应用-古代数学问题
3.【答案】B
【知识点】二元一次方程组的应用-几何问题
4.【答案】C
【知识点】二元一次方程组的其他应用
5.【答案】B
【知识点】二元一次方程组的应用-古代数学问题
6.【答案】A
【知识点】二元一次方程组的应用-数字问题
7.【答案】A
【知识点】二元一次方程组的应用-古代数学问题
8.【答案】A
【知识点】二元一次方程组的应用-古代数学问题
9.【答案】B
【知识点】二元一次方程组的应用-古代数学问题
10.【答案】A
【知识点】二元一次方程组的应用-几何问题
11.【答案】675
【知识点】二元一次方程组的应用-几何问题
12.【答案】
【知识点】二元一次方程组的其他应用
13.【答案】
【知识点】二元一次方程组的应用-古代数学问题
14.【答案】16
【知识点】二元一次方程组的应用-数字问题
15.【答案】5
【知识点】二元一次方程组的应用-几何问题
16.【答案】5:11
【知识点】二元一次方程组的实际应用-配套问题
17.【答案】(1)元、元的笔记本分别买了本和本
(2)不可能
【知识点】一元一次方程的其他应用;二元一次方程组的实际应用-销售问题
18.【答案】(1)小华家离学校700米
(2)小华从学校到家里到达中点的时间比小华从家里到学校到达中点的时间要多一些
【知识点】有理数混合运算的实际应用;二元一次方程组的实际应用-行程问题
19.【答案】两种购买方法:甲种型号手机购买30部,乙种型号手机购买10部;或甲种型号手机购买20部,丙种型号手机购买20部
【知识点】二元一次方程组的实际应用-方案选择题问题
20.【答案】分配40名工人生产螺栓,50名工人生产螺帽.
【知识点】二元一次方程组的实际应用-配套问题
21.【答案】解:设一匹马价x两,一头牛价y两,
由题意得:
解得:
答:一匹马价6两,一头牛价4两
【知识点】二元一次方程组的应用-古代数学问题
22.【答案】(1),
(2)故制作种木盒100个,制作种木盒100个,使用甲种方式切割的木板150张,使用乙种方式切割的木板材50张.
(3)
【知识点】二元一次方程组的其他应用
23.【答案】解:任务1:设A型咖啡的每杯价格为x元,B型咖啡每杯价格为y元
由题可知:
解得;
答:A型咖啡的每杯价格为8元,B型咖啡每杯价格为10元;
任务2:设A型咖啡为m:杯 ,B型咖啡为n杯
则8m+10n=200
解得:,,, ,
∴共有四种方案;
任务3:买了6杯,理由如下:
设A型不加料为a杯 ,总的杯数为3a杯,设A型的加料和B型的不加料为b杯,则B型的加料为(2a-b)杯,
∴8a+10b+12(2a-b)=208
∴
因为a是整数
所以b=8,a=7
b=24 ,a=89不合题意
所以2a-b=2×7-8=6 ,即B型加料的咖啡买了6杯.
【知识点】二元一次方程的应用;二元一次方程组的实际应用-销售问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
