4.1 立体图形与平面图形 同步练习(含答案)
文档属性
| 名称 | 4.1 立体图形与平面图形 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 528.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-28 15:38:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
4.1 立体图形与平面图形
一、单选题
1.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“中”字所在面相对的面上的汉字是( )
A.梦 B.聚 C.力 D.凝
2.(2021七上·洪山期末)如图是一个正方体的展开图,把展开图折叠成正方体后,有“国”字一面的对面上的字是( )
A.诚 B.信 C.友 D.善
3.下面四个立体图形中,和其他三个立体图形不同类型的是( )
A. B.
C. D.
4.(2024七上·莲池期末)某几何体的表面展开图如图所示,那么这个几何体是( )
A.圆锥 B.圆柱 C.三棱柱 D.三棱锥
5.(2020七上·睢宁月考)不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱,该模型的形状对应的立体图形可能是( )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
6.如图,把展开图沿虚线折叠成一个正方体后,相对面上的两数之和都相等,则的值为( )
A.8 B.6 C.5 D.4
7.(2021七上·榆次期中)2021年是第七届全国文明城市创建周期的开局之年我市全体市民积极行动,全力以赴投入到全国文明城市的创建攻坚战中小明同学制作了如图所示的标有创建全国文明城市宣传标语的正方体平面展开图,由图可知,与原正方体“中”字所在面相对的面上标的汉字是( )
A.做 B.文 C.明 D.人
8.(2021·苏家屯模拟)如图是一个正方体的表面展开图,则图中“加”字所在面的对面所标的字是( )
A.北 B.运 C.奥 D.京
9.长方体的顶点数、棱数、面数分别是( )
A.8,10,6 B.6,12,8 C.6,8,10 D.8,12,6
10.(2015九上·新泰竞赛)由若干个同样大小的正方体堆积成一个实物,从不同侧面观察到如图所示的投影图,则构成该实物的小正方体个数为( ).
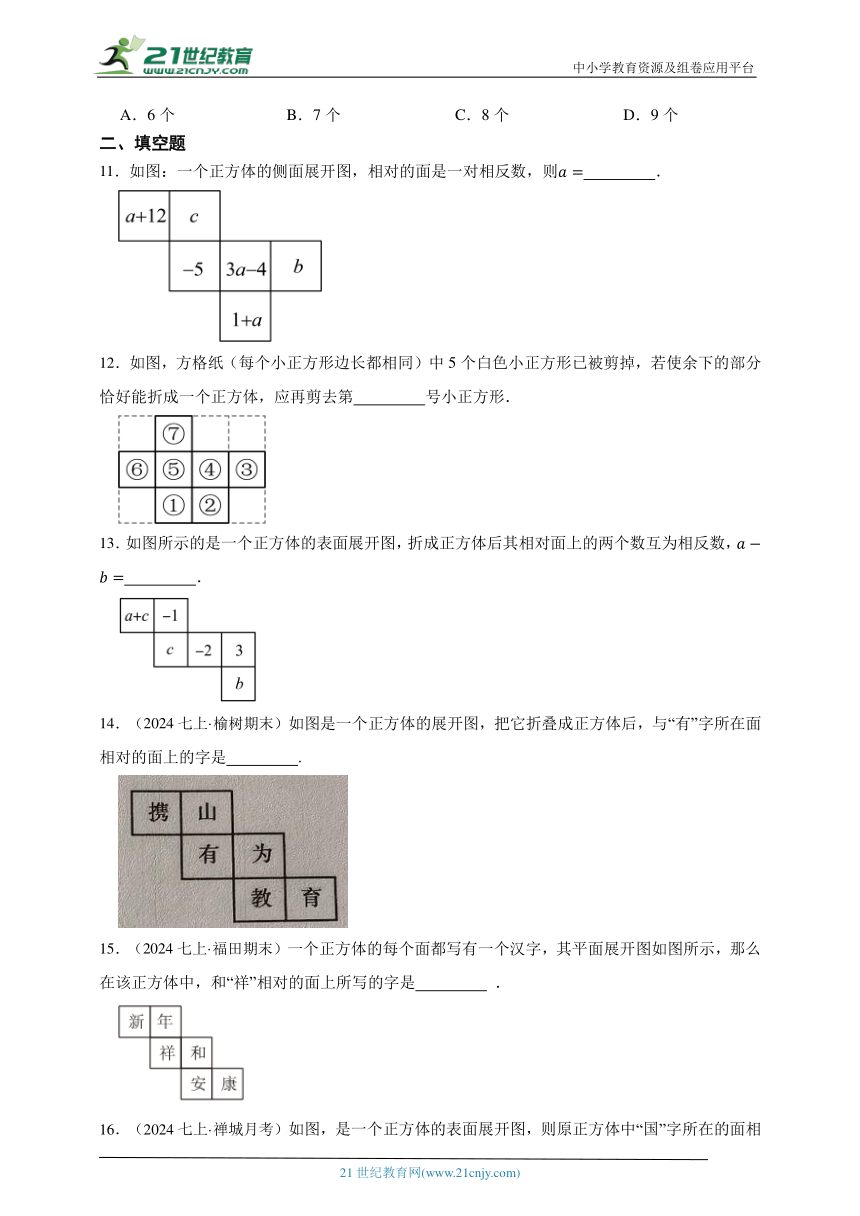
A.6个 B.7个 C.8个 D.9个
二、填空题
11.如图:一个正方体的侧面展开图,相对的面是一对相反数,则 .
12.如图,方格纸(每个小正方形边长都相同)中5个白色小正方形已被剪掉,若使余下的部分恰好能折成一个正方体,应再剪去第 号小正方形.
13.如图所示的是一个正方体的表面展开图,折成正方体后其相对面上的两个数互为相反数, .
14.(2024七上·榆树期末)如图是一个正方体的展开图,把它折叠成正方体后,与“有”字所在面相对的面上的字是 .
15.(2024七上·福田期末)一个正方体的每个面都写有一个汉字,其平面展开图如图所示,那么在该正方体中,和“祥”相对的面上所写的字是 .
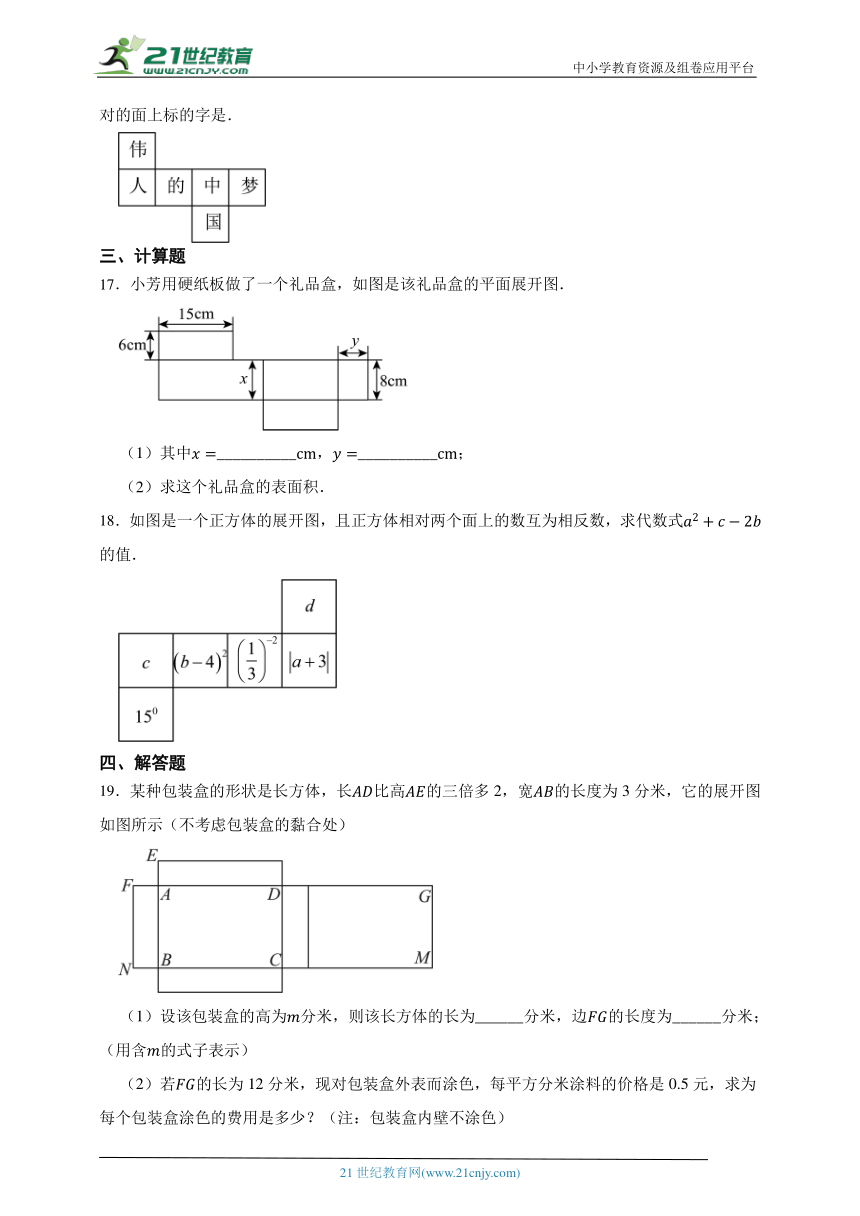
16.(2024七上·禅城月考)如图,是一个正方体的表面展开图,则原正方体中“国”字所在的面相对的面上标的字是.
三、计算题
17.小芳用硬纸板做了一个礼品盒,如图是该礼品盒的平面展开图.
(1)其中__________,__________;
(2)求这个礼品盒的表面积.
18.如图是一个正方体的展开图,且正方体相对两个面上的数互为相反数,求代数式的值.
四、解答题
19.某种包装盒的形状是长方体,长比高的三倍多2,宽的长度为3分米,它的展开图如图所示(不考虑包装盒的黏合处)
(1)设该包装盒的高为分米,则该长方体的长为______分米,边的长度为______分米;(用含的式子表示)
(2)若的长为12分米,现对包装盒外表而涂色,每平方分米涂料的价格是0.5元,求为每个包装盒涂色的费用是多少?(注:包装盒内壁不涂色)
20.(2023七上·五华期中)妈妈给圆柱形的玻璃杯(底面直径16cm,高20cm)做了一个布套(包住侧面)
(1)求出至少用布料多少平方厘米?
(2)求这个杯子最多可以盛水多少立方厘米?
21.(2023七上·清苑期中)如图1,该三棱柱的高为,底面是一个每条边长都为的三角形.
(1)这个三棱柱有 个面,有 条棱.
(2)如图2,这是该三棱柱的表面展开图的一部分,请将它补充完整.
(3)这个三棱柱的侧面积是 ,要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最大值为 .
22.对于如图①、②、③、④所示的四个平面图
我们规定:如图③,它的顶点为A、B、C、D、E共5个,区域为AED、ABE、BEC、CED共4个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条.
(1)按此规定将图①、②、④的顶点①数、边数、区域数填入下列表格:
图 顶点数 边数 区域数
①
②
③ 5 8 4
④
(2)观察上表,请你归纳上述平面图的顶点数、边数、区域数之间的数量关系.
(3)若有一个平面图满足(2)中归纳所得的数量关系,它共有9个区域,且每一个顶点出发都有3条边,则这个平面图共有多少条边?
答案解析部分
1.【答案】D
【知识点】含图案的正方体的展开图
2.【答案】B
【知识点】几何体的展开图
3.【答案】B
【知识点】立体图形的概念与分类
4.【答案】C
【知识点】几何体的展开图
5.【答案】D
【知识点】立体图形的概念与分类
6.【答案】B
【知识点】有理数的减法法则;求代数式的值-整体代入求值;含图案的正方体的展开图
7.【答案】B
【知识点】几何体的展开图
8.【答案】D
【知识点】几何体的展开图
9.【答案】D
【知识点】立体图形的概念与分类
10.【答案】B
【知识点】立体图形的概念与分类
11.【答案】
【知识点】含图案的正方体的展开图
12.【答案】①或②
【知识点】正方体的几种展开图的识别
13.【答案】1
【知识点】几何体的展开图;含图案的正方体的展开图
14.【答案】育
【知识点】几何体的展开图
15.【答案】康
【知识点】几何体的展开图
16.【答案】伟
【知识点】含图案的正方体的展开图
17.【答案】(1),
(2)
【知识点】几何体的展开图;已知展开图进行几何体的相关的计算
18.【答案】
【知识点】绝对值的非负性;相反数的意义与性质;求代数式的值-直接代入求值;含图案的正方体的展开图
19.【答案】(1),
(2)为每个包装盒涂色的费用是23元
【知识点】几何体的展开图;已知展开图进行几何体的相关的计算
20.【答案】(1)至少用布料448π平方厘米
(2)这个杯子最多可以盛水1280π立方厘米
【知识点】已知展开图进行几何体的相关的计算
21.【答案】(1)5;9
(2)解:如图所示(画法不唯一).
(3)135;37
【知识点】几何体的展开图
22.【答案】解:(1)按此规定将图①、②、④的顶点数、边数、区域数填入下列表格:
图 顶点数 边数 区域数
① 4 6 3
② 6 9 4
③ 5 8 4
④ 10 15 6
(2)由表格得:顶点数+区域数=边数+1,
(3)设顶点数为x,根据题意可知,x+9= +1,
得出x=16
每个顶点发出三个3边,有9个区域数,
则有16个顶点,24条边.
【知识点】平面图形的初步认识
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.1 立体图形与平面图形
一、单选题
1.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“中”字所在面相对的面上的汉字是( )
A.梦 B.聚 C.力 D.凝
2.(2021七上·洪山期末)如图是一个正方体的展开图,把展开图折叠成正方体后,有“国”字一面的对面上的字是( )
A.诚 B.信 C.友 D.善
3.下面四个立体图形中,和其他三个立体图形不同类型的是( )
A. B.
C. D.
4.(2024七上·莲池期末)某几何体的表面展开图如图所示,那么这个几何体是( )
A.圆锥 B.圆柱 C.三棱柱 D.三棱锥
5.(2020七上·睢宁月考)不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱,该模型的形状对应的立体图形可能是( )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
6.如图,把展开图沿虚线折叠成一个正方体后,相对面上的两数之和都相等,则的值为( )
A.8 B.6 C.5 D.4
7.(2021七上·榆次期中)2021年是第七届全国文明城市创建周期的开局之年我市全体市民积极行动,全力以赴投入到全国文明城市的创建攻坚战中小明同学制作了如图所示的标有创建全国文明城市宣传标语的正方体平面展开图,由图可知,与原正方体“中”字所在面相对的面上标的汉字是( )
A.做 B.文 C.明 D.人
8.(2021·苏家屯模拟)如图是一个正方体的表面展开图,则图中“加”字所在面的对面所标的字是( )
A.北 B.运 C.奥 D.京
9.长方体的顶点数、棱数、面数分别是( )
A.8,10,6 B.6,12,8 C.6,8,10 D.8,12,6
10.(2015九上·新泰竞赛)由若干个同样大小的正方体堆积成一个实物,从不同侧面观察到如图所示的投影图,则构成该实物的小正方体个数为( ).
A.6个 B.7个 C.8个 D.9个
二、填空题
11.如图:一个正方体的侧面展开图,相对的面是一对相反数,则 .
12.如图,方格纸(每个小正方形边长都相同)中5个白色小正方形已被剪掉,若使余下的部分恰好能折成一个正方体,应再剪去第 号小正方形.
13.如图所示的是一个正方体的表面展开图,折成正方体后其相对面上的两个数互为相反数, .
14.(2024七上·榆树期末)如图是一个正方体的展开图,把它折叠成正方体后,与“有”字所在面相对的面上的字是 .
15.(2024七上·福田期末)一个正方体的每个面都写有一个汉字,其平面展开图如图所示,那么在该正方体中,和“祥”相对的面上所写的字是 .
16.(2024七上·禅城月考)如图,是一个正方体的表面展开图,则原正方体中“国”字所在的面相对的面上标的字是.
三、计算题
17.小芳用硬纸板做了一个礼品盒,如图是该礼品盒的平面展开图.
(1)其中__________,__________;
(2)求这个礼品盒的表面积.
18.如图是一个正方体的展开图,且正方体相对两个面上的数互为相反数,求代数式的值.
四、解答题
19.某种包装盒的形状是长方体,长比高的三倍多2,宽的长度为3分米,它的展开图如图所示(不考虑包装盒的黏合处)
(1)设该包装盒的高为分米,则该长方体的长为______分米,边的长度为______分米;(用含的式子表示)
(2)若的长为12分米,现对包装盒外表而涂色,每平方分米涂料的价格是0.5元,求为每个包装盒涂色的费用是多少?(注:包装盒内壁不涂色)
20.(2023七上·五华期中)妈妈给圆柱形的玻璃杯(底面直径16cm,高20cm)做了一个布套(包住侧面)
(1)求出至少用布料多少平方厘米?
(2)求这个杯子最多可以盛水多少立方厘米?
21.(2023七上·清苑期中)如图1,该三棱柱的高为,底面是一个每条边长都为的三角形.
(1)这个三棱柱有 个面,有 条棱.
(2)如图2,这是该三棱柱的表面展开图的一部分,请将它补充完整.
(3)这个三棱柱的侧面积是 ,要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最大值为 .
22.对于如图①、②、③、④所示的四个平面图
我们规定:如图③,它的顶点为A、B、C、D、E共5个,区域为AED、ABE、BEC、CED共4个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条.
(1)按此规定将图①、②、④的顶点①数、边数、区域数填入下列表格:
图 顶点数 边数 区域数
①
②
③ 5 8 4
④
(2)观察上表,请你归纳上述平面图的顶点数、边数、区域数之间的数量关系.
(3)若有一个平面图满足(2)中归纳所得的数量关系,它共有9个区域,且每一个顶点出发都有3条边,则这个平面图共有多少条边?
答案解析部分
1.【答案】D
【知识点】含图案的正方体的展开图
2.【答案】B
【知识点】几何体的展开图
3.【答案】B
【知识点】立体图形的概念与分类
4.【答案】C
【知识点】几何体的展开图
5.【答案】D
【知识点】立体图形的概念与分类
6.【答案】B
【知识点】有理数的减法法则;求代数式的值-整体代入求值;含图案的正方体的展开图
7.【答案】B
【知识点】几何体的展开图
8.【答案】D
【知识点】几何体的展开图
9.【答案】D
【知识点】立体图形的概念与分类
10.【答案】B
【知识点】立体图形的概念与分类
11.【答案】
【知识点】含图案的正方体的展开图
12.【答案】①或②
【知识点】正方体的几种展开图的识别
13.【答案】1
【知识点】几何体的展开图;含图案的正方体的展开图
14.【答案】育
【知识点】几何体的展开图
15.【答案】康
【知识点】几何体的展开图
16.【答案】伟
【知识点】含图案的正方体的展开图
17.【答案】(1),
(2)
【知识点】几何体的展开图;已知展开图进行几何体的相关的计算
18.【答案】
【知识点】绝对值的非负性;相反数的意义与性质;求代数式的值-直接代入求值;含图案的正方体的展开图
19.【答案】(1),
(2)为每个包装盒涂色的费用是23元
【知识点】几何体的展开图;已知展开图进行几何体的相关的计算
20.【答案】(1)至少用布料448π平方厘米
(2)这个杯子最多可以盛水1280π立方厘米
【知识点】已知展开图进行几何体的相关的计算
21.【答案】(1)5;9
(2)解:如图所示(画法不唯一).
(3)135;37
【知识点】几何体的展开图
22.【答案】解:(1)按此规定将图①、②、④的顶点数、边数、区域数填入下列表格:
图 顶点数 边数 区域数
① 4 6 3
② 6 9 4
③ 5 8 4
④ 10 15 6
(2)由表格得:顶点数+区域数=边数+1,
(3)设顶点数为x,根据题意可知,x+9= +1,
得出x=16
每个顶点发出三个3边,有9个区域数,
则有16个顶点,24条边.
【知识点】平面图形的初步认识
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
