第4章 图形的认识 单元测试(含答案)
文档属性
| 名称 | 第4章 图形的认识 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 403.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-28 18:59:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第4章 图形的认识
一、单选题
1.(2020七上·三明月考)下列三种现象中,可用“两点之间线段最短”来解释的现象是( )
(1)用一个钉子把一根细木条钉在木板上,用手拨木条,木条能转动;(2)过马路时,行人选择横穿马路而不走人行天桥;(3)工人砌砖前需要固定两点,牵上线,才开始砌砖.
A.(1) B.(2) C.(2)(3) D.都不可以
2.下列说法正确的是( )
A.画直线厘米
B.画射线厘米
C.在10厘米的射线上截取厘米
D.延长线段到点C,使
3.下列说法:
①把弯曲的河道改直,能够缩短航程,这是由于两点之间,线段最短;
②射线与射线是同一条射线;
③连接两点的线段叫做这两点的距离;
④将一根细木条固定在墙上,至少需要两根钉子,是因为两点确定一条直线.
其中说法正确的有( )
A.① ③ B.① ④ C.① ③ ④ D.② ③
4.如图,把弯曲的河道改直,能够缩短航程.这样做根据的道理是( )
A.两点之间,线段最短 B.两点确定一条直线
C.两点之间,直线最短 D.两点确定一条线段
5.已知点在线段上,,点,在线段上,点在点的左侧.若,线段在线段上移动,且满足关系式,则的值为( )
A. B. C.或 D.
6.几何体的展开图图形经过折叠不能围成棱柱的是( )
A. B.
C. D.
7.(2024九下·深圳月考)如图是一个正方体的展开图,则与”学”字相对的是( )
A.核 B.心 C.数 D.养
8.(2024八下·麒麟期中) 如图,将长方形和直角三角形的直角顶点重合,若,则的度数为( )
A. B. C. D.
9.如图所示,C、D是线段AB上两点,若AC=3cm,C为AD中点且AB=10cm,则DB=( )
A.4cm B.5cm C.6cm D.7cm
10.(2025七下·南宁开学考)如图,为直线上一点,为直角,平分,平分,平分.下列结论:①与互为余角;②;③与互为补角;④.其中结论正确的序号是( )
A.①②④ B.③④ C.②③ D.②③④
二、填空题
11.(2018七上·抚州期末)25 26 36"+114 15 42"= .
12.(2023七上·孝南期末) °.
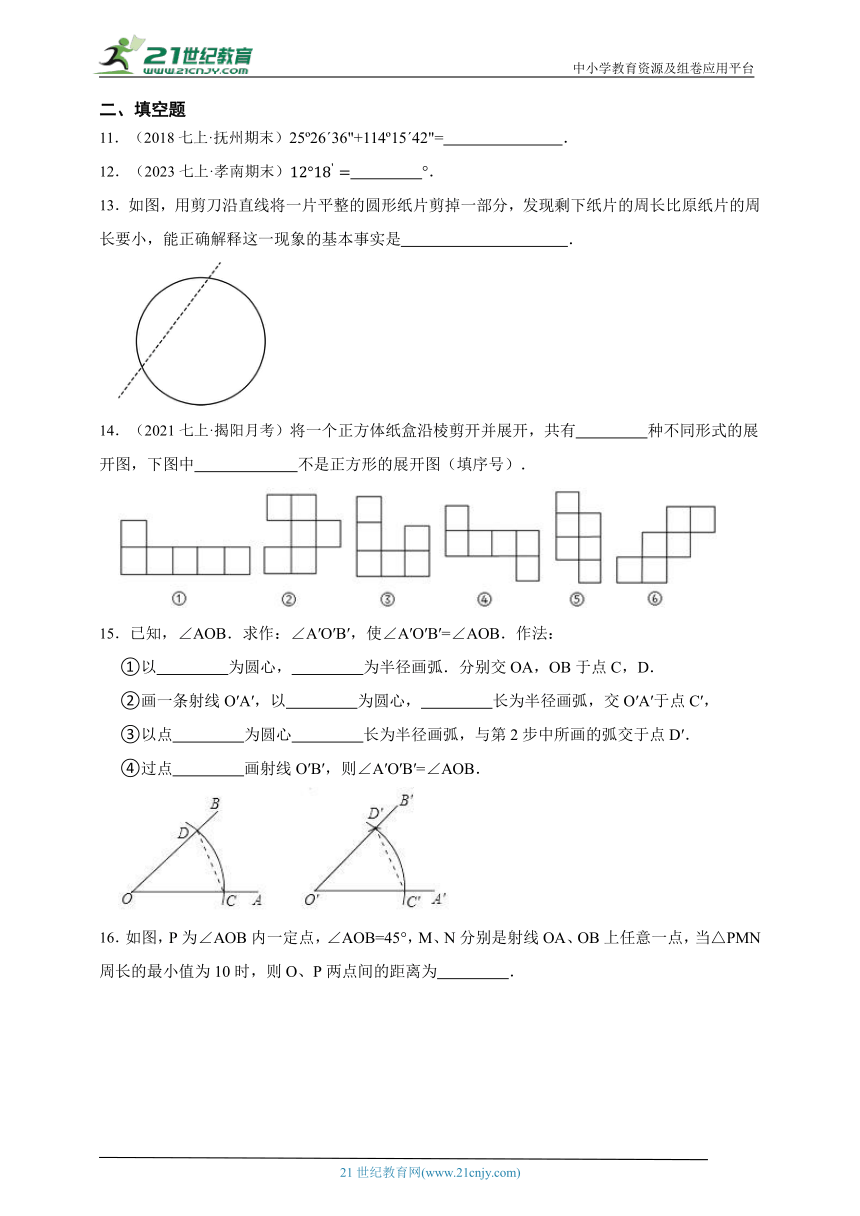
13.如图,用剪刀沿直线将一片平整的圆形纸片剪掉一部分,发现剩下纸片的周长比原纸片的周长要小,能正确解释这一现象的基本事实是 .
14.(2021七上·揭阳月考)将一个正方体纸盒沿棱剪开并展开,共有 种不同形式的展开图,下图中 不是正方形的展开图(填序号).
15.已知,∠AOB.求作:∠A′O′B′,使∠A′O′B′=∠AOB.作法:
①以 为圆心, 为半径画弧.分别交OA,OB于点C,D.
②画一条射线O′A′,以 为圆心, 长为半径画弧,交O′A′于点C′,
③以点 为圆心 长为半径画弧,与第2步中所画的弧交于点D′.
④过点 画射线O′B′,则∠A′O′B′=∠AOB.
16.如图,P为∠AOB内一定点,∠AOB=45°,M、N分别是射线OA、OB上任意一点,当△PMN周长的最小值为10时,则O、P两点间的距离为 .
三、计算题
17.如图,点C在线段上,点M,N分别是线段的中点.
(1)若,求线段的长;
(2)若,求线段的长度.
18.(2019七上·陇西期中)如图是一个正方体的平面展开图,若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和均为5,求x+y+z的值.
19.如图,在数轴上的A点表示数,B点表示数,满足
(1)点A表示的数为____________,点B表示的数为______________.
(2)若在原点处放一挡板,一小球甲从点A 处以2个单位/秒的速度向左运动;同时另一小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒).
①当时,乙小球到原点的距离=__________________;
当时,乙小球到原点的距离=__________________.
②试探究:甲、乙两小球到原点的距离可能相等吗?若不能,请说明理由;若能,请计算说明.
(3)现将小球乙看成动点P,当点P运动到线段上时,分别取和的中点,试判断的值是否为定值,若不是,请说明理由;若是,请求出该定值.
四、解答题
20.(2023七上·镇海区期中)如图,数轴上有A,B两点,A,B之间距离为15,原点O在A,B之间,O到A的距离是O到B的距离的两倍.
(1)点A表示的数为 ,点B表示的数为 ;
(2)点A、点B和点P(点P初始位置在原点O)同时向左运动,它们的速度分别为1,2,2个单位长度每秒,则经过多少秒,点P到点A与点B的距离相等?
(3)点B沿着数轴移动,每次只允许移动1个单位长度,经过6次移动后,点B与原点O相距1个单位长度.满足条件的点B的移动方法共有多少种?
(4)点A和点B同时沿着数轴移动,两点每次均只允许移动1个单位长度.请判断点A和点B经过相同次数的移动后,能否同时到达原点O?如果能,请给出点A和点B各自的移动方法;如果不能,请说明理由.
21.如图,为线段上一点,为的中点,,.
(1)求的长;
(2)若点E在线段上,且,求的长.
22.(2020七上·含山期末)如图,已知点M是线段AB的中点,点E将AB分成 的两段,若 ,求线段AB的长度.
23.(2024七上·苏州月考)如图①,在数轴上有一条线段AB,点A,B表示的数分别是﹣2和﹣11.
(1)若M是线段AB的中点,则点M在数轴上对应的数为 .
(2)若C为线段AB上一点,如图②,以点C为折点,将此数轴向右对折;如图③,点B落在点A的右边点B'处,若AB'=B'C,求点C在数轴上对应的数是多少?
答案解析部分
1.【答案】B
【知识点】两点确定一条直线;两点之间线段最短
2.【答案】D
【知识点】直线、射线、线段;尺规作图-直线、射线、线段
3.【答案】B
【知识点】直线、射线、线段;两点确定一条直线;两点之间线段最短
4.【答案】A
【知识点】两点之间线段最短
5.【答案】B
【知识点】线段的和、差、倍、分的简单计算
6.【答案】D
【知识点】立体图形的概念与分类;平面图形的初步认识;几何体的展开图
7.【答案】B
【知识点】几何体的展开图
8.【答案】C
【知识点】角的运算
9.【答案】A
【知识点】线段的中点
10.【答案】D
【知识点】角的运算;角平分线的概念
11.【答案】139 42 18"
【知识点】常用角的度量单位及换算
12.【答案】
【知识点】常用角的度量单位及换算
13.【答案】两点之间线段最短
【知识点】两点之间线段最短
14.【答案】11;①②③⑤
【知识点】几何体的展开图
15.【答案】O;任意长;O′;OC;C;CD;D′
【知识点】尺规作图-作一个角等于已知角
16.【答案】5
【知识点】两点之间线段最短
17.【答案】(1)
(2)
【知识点】线段的中点;线段的和、差、倍、分的简单计算
18.【答案】解:由于正方体的平面展开图共有六个面,
其中面“z”与面“3”相对,面“y”与面“-2”相对,面“x”与面“10”相对,
则z+3=5,y+(-2)=5,x+10=5
解得z=2,y=7,x=-5
故x+y+z=4
【知识点】几何体的展开图
19.【答案】(1),5
(2)①2,4;②能,当或时,甲、乙两小球到原点的距离相等
(3)的值是定值,这个定值为2
【知识点】整式的加减运算;线段的中点;一元一次方程的实际应用-几何问题
20.【答案】(1)-10;5
(2)解:设经过t秒,点P到点A与点B的距离相等,
则:|-2t-(-10-t)|=|-2t-(5-2t)|,
解得:t=15或t=5,
答:经过5或15秒,点P到点A与点B的距离相等;
(3)解:①点B沿着数轴向左移动,经过6次移动后,点B对应的数为-1,此时点B与原点O相距1个单位长度;
②点B沿着数轴先向右移动1次,再向左移动5次,经过6次移动后,点B对应的数为1,此时点B与原点O相距1个单位长度;
③点B沿着数轴先向左移动5次,再向右移动1次,经过6次移动后,点B对应的数为1,此时点B与原点O相距1个单位长度;
∴满足条件的点B的移动方法共有3种;
(4)解:点A和点B经过10次数的移动后,能同时到达原点O.
移动方法:点A向右移动10次到达原点O,点B先向左移动2次再向右移动1次,接着向左移动2次再向右移动1次,再接着向左移动2次再向右移动1次,再向左移动1次,共10次到达原点O.
【知识点】数轴及有理数在数轴上的表示;一元一次方程的其他应用;线段上的两点间的距离
21.【答案】(1);
(2)或.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
22.【答案】解:∵点E将AB分成 的两段,设AE=3k,BE=4k,
∴AB=AE+BE=3k+4k=7k,
∵点M是线段AB的中点,
∴AM= ,
∴EM=AM-AE= =2cm,
∴k=4cm,
∴AB=7k=7×4=28cm.
∴线段AB的长为28cm.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
23.【答案】(1)-6.5;(2)-6
【知识点】一元一次方程的实际应用-几何问题;线段的和、差、倍、分的简单计算
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第4章 图形的认识
一、单选题
1.(2020七上·三明月考)下列三种现象中,可用“两点之间线段最短”来解释的现象是( )
(1)用一个钉子把一根细木条钉在木板上,用手拨木条,木条能转动;(2)过马路时,行人选择横穿马路而不走人行天桥;(3)工人砌砖前需要固定两点,牵上线,才开始砌砖.
A.(1) B.(2) C.(2)(3) D.都不可以
2.下列说法正确的是( )
A.画直线厘米
B.画射线厘米
C.在10厘米的射线上截取厘米
D.延长线段到点C,使
3.下列说法:
①把弯曲的河道改直,能够缩短航程,这是由于两点之间,线段最短;
②射线与射线是同一条射线;
③连接两点的线段叫做这两点的距离;
④将一根细木条固定在墙上,至少需要两根钉子,是因为两点确定一条直线.
其中说法正确的有( )
A.① ③ B.① ④ C.① ③ ④ D.② ③
4.如图,把弯曲的河道改直,能够缩短航程.这样做根据的道理是( )
A.两点之间,线段最短 B.两点确定一条直线
C.两点之间,直线最短 D.两点确定一条线段
5.已知点在线段上,,点,在线段上,点在点的左侧.若,线段在线段上移动,且满足关系式,则的值为( )
A. B. C.或 D.
6.几何体的展开图图形经过折叠不能围成棱柱的是( )
A. B.
C. D.
7.(2024九下·深圳月考)如图是一个正方体的展开图,则与”学”字相对的是( )
A.核 B.心 C.数 D.养
8.(2024八下·麒麟期中) 如图,将长方形和直角三角形的直角顶点重合,若,则的度数为( )
A. B. C. D.
9.如图所示,C、D是线段AB上两点,若AC=3cm,C为AD中点且AB=10cm,则DB=( )
A.4cm B.5cm C.6cm D.7cm
10.(2025七下·南宁开学考)如图,为直线上一点,为直角,平分,平分,平分.下列结论:①与互为余角;②;③与互为补角;④.其中结论正确的序号是( )
A.①②④ B.③④ C.②③ D.②③④
二、填空题
11.(2018七上·抚州期末)25 26 36"+114 15 42"= .
12.(2023七上·孝南期末) °.
13.如图,用剪刀沿直线将一片平整的圆形纸片剪掉一部分,发现剩下纸片的周长比原纸片的周长要小,能正确解释这一现象的基本事实是 .
14.(2021七上·揭阳月考)将一个正方体纸盒沿棱剪开并展开,共有 种不同形式的展开图,下图中 不是正方形的展开图(填序号).
15.已知,∠AOB.求作:∠A′O′B′,使∠A′O′B′=∠AOB.作法:
①以 为圆心, 为半径画弧.分别交OA,OB于点C,D.
②画一条射线O′A′,以 为圆心, 长为半径画弧,交O′A′于点C′,
③以点 为圆心 长为半径画弧,与第2步中所画的弧交于点D′.
④过点 画射线O′B′,则∠A′O′B′=∠AOB.
16.如图,P为∠AOB内一定点,∠AOB=45°,M、N分别是射线OA、OB上任意一点,当△PMN周长的最小值为10时,则O、P两点间的距离为 .
三、计算题
17.如图,点C在线段上,点M,N分别是线段的中点.
(1)若,求线段的长;
(2)若,求线段的长度.
18.(2019七上·陇西期中)如图是一个正方体的平面展开图,若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和均为5,求x+y+z的值.
19.如图,在数轴上的A点表示数,B点表示数,满足
(1)点A表示的数为____________,点B表示的数为______________.
(2)若在原点处放一挡板,一小球甲从点A 处以2个单位/秒的速度向左运动;同时另一小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒).
①当时,乙小球到原点的距离=__________________;
当时,乙小球到原点的距离=__________________.
②试探究:甲、乙两小球到原点的距离可能相等吗?若不能,请说明理由;若能,请计算说明.
(3)现将小球乙看成动点P,当点P运动到线段上时,分别取和的中点,试判断的值是否为定值,若不是,请说明理由;若是,请求出该定值.
四、解答题
20.(2023七上·镇海区期中)如图,数轴上有A,B两点,A,B之间距离为15,原点O在A,B之间,O到A的距离是O到B的距离的两倍.
(1)点A表示的数为 ,点B表示的数为 ;
(2)点A、点B和点P(点P初始位置在原点O)同时向左运动,它们的速度分别为1,2,2个单位长度每秒,则经过多少秒,点P到点A与点B的距离相等?
(3)点B沿着数轴移动,每次只允许移动1个单位长度,经过6次移动后,点B与原点O相距1个单位长度.满足条件的点B的移动方法共有多少种?
(4)点A和点B同时沿着数轴移动,两点每次均只允许移动1个单位长度.请判断点A和点B经过相同次数的移动后,能否同时到达原点O?如果能,请给出点A和点B各自的移动方法;如果不能,请说明理由.
21.如图,为线段上一点,为的中点,,.
(1)求的长;
(2)若点E在线段上,且,求的长.
22.(2020七上·含山期末)如图,已知点M是线段AB的中点,点E将AB分成 的两段,若 ,求线段AB的长度.
23.(2024七上·苏州月考)如图①,在数轴上有一条线段AB,点A,B表示的数分别是﹣2和﹣11.
(1)若M是线段AB的中点,则点M在数轴上对应的数为 .
(2)若C为线段AB上一点,如图②,以点C为折点,将此数轴向右对折;如图③,点B落在点A的右边点B'处,若AB'=B'C,求点C在数轴上对应的数是多少?
答案解析部分
1.【答案】B
【知识点】两点确定一条直线;两点之间线段最短
2.【答案】D
【知识点】直线、射线、线段;尺规作图-直线、射线、线段
3.【答案】B
【知识点】直线、射线、线段;两点确定一条直线;两点之间线段最短
4.【答案】A
【知识点】两点之间线段最短
5.【答案】B
【知识点】线段的和、差、倍、分的简单计算
6.【答案】D
【知识点】立体图形的概念与分类;平面图形的初步认识;几何体的展开图
7.【答案】B
【知识点】几何体的展开图
8.【答案】C
【知识点】角的运算
9.【答案】A
【知识点】线段的中点
10.【答案】D
【知识点】角的运算;角平分线的概念
11.【答案】139 42 18"
【知识点】常用角的度量单位及换算
12.【答案】
【知识点】常用角的度量单位及换算
13.【答案】两点之间线段最短
【知识点】两点之间线段最短
14.【答案】11;①②③⑤
【知识点】几何体的展开图
15.【答案】O;任意长;O′;OC;C;CD;D′
【知识点】尺规作图-作一个角等于已知角
16.【答案】5
【知识点】两点之间线段最短
17.【答案】(1)
(2)
【知识点】线段的中点;线段的和、差、倍、分的简单计算
18.【答案】解:由于正方体的平面展开图共有六个面,
其中面“z”与面“3”相对,面“y”与面“-2”相对,面“x”与面“10”相对,
则z+3=5,y+(-2)=5,x+10=5
解得z=2,y=7,x=-5
故x+y+z=4
【知识点】几何体的展开图
19.【答案】(1),5
(2)①2,4;②能,当或时,甲、乙两小球到原点的距离相等
(3)的值是定值,这个定值为2
【知识点】整式的加减运算;线段的中点;一元一次方程的实际应用-几何问题
20.【答案】(1)-10;5
(2)解:设经过t秒,点P到点A与点B的距离相等,
则:|-2t-(-10-t)|=|-2t-(5-2t)|,
解得:t=15或t=5,
答:经过5或15秒,点P到点A与点B的距离相等;
(3)解:①点B沿着数轴向左移动,经过6次移动后,点B对应的数为-1,此时点B与原点O相距1个单位长度;
②点B沿着数轴先向右移动1次,再向左移动5次,经过6次移动后,点B对应的数为1,此时点B与原点O相距1个单位长度;
③点B沿着数轴先向左移动5次,再向右移动1次,经过6次移动后,点B对应的数为1,此时点B与原点O相距1个单位长度;
∴满足条件的点B的移动方法共有3种;
(4)解:点A和点B经过10次数的移动后,能同时到达原点O.
移动方法:点A向右移动10次到达原点O,点B先向左移动2次再向右移动1次,接着向左移动2次再向右移动1次,再接着向左移动2次再向右移动1次,再向左移动1次,共10次到达原点O.
【知识点】数轴及有理数在数轴上的表示;一元一次方程的其他应用;线段上的两点间的距离
21.【答案】(1);
(2)或.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
22.【答案】解:∵点E将AB分成 的两段,设AE=3k,BE=4k,
∴AB=AE+BE=3k+4k=7k,
∵点M是线段AB的中点,
∴AM= ,
∴EM=AM-AE= =2cm,
∴k=4cm,
∴AB=7k=7×4=28cm.
∴线段AB的长为28cm.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
23.【答案】(1)-6.5;(2)-6
【知识点】一元一次方程的实际应用-几何问题;线段的和、差、倍、分的简单计算
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
