教科版高中物理必修第一册 第一章 描述运动的基本概念 2 位置位移 课件(共58张PPT)
文档属性
| 名称 | 教科版高中物理必修第一册 第一章 描述运动的基本概念 2 位置位移 课件(共58张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-28 19:53:12 | ||
图片预览











文档简介
(共58张PPT)
2.位置 位移
第一章 描述运动的基本概念
1.会选择坐标系描述位置。
2.理解位移的概念,会区分位移和路程的不同。
3.理解位移—时间图像的意义。
素养目标
知识点一 确定质点位置的方法——坐标系
自主学习
情境导入 某段平直公路沿线每隔1 km设置一块用以指示相对起点的里程碑。
(1)如果以某一里程碑为起点,司机能不能确定在某段时间内所走的距离?
提示:能
(2)如果以某一里程碑为起点,以司机行驶的方向为正方向,是否能看成数轴?
提示:能
教材梳理 (阅读教材P7—P8完成下列填空)
1.坐标系及坐标
要准确地描述质点的位置,需要建立__________,即按照规定的方法选取一组________的数来描述它的________,这组有序的数就是“坐标”。
2.坐标系的种类
(1)一维坐标系:物体沿一条直线运动,要准确描述物体的位置需建立____________坐标系。
(2)二维坐标系:确定地球表面物体的位置常用的坐标系是经纬度,它是固定在地球表面上的二维平面直角坐标系。
(3)三维坐标系:像空中飞行的物体,要准确描述其位置,除经纬度外,还需要高度的数值,这就是三维空间直角坐标系。
坐标系
有序
位置
一维直线
课堂探究
师生互动 观察下列三种运动情景,回答下列问题:
任务1.描述百米赛跑运动员在运动中的位置,应该建立怎样的坐标系?
提示:以起点为坐标原点,建立一维直线坐标系。
任务2.描述冰场上花样滑冰运动员的位置,应该建立怎样的坐标系?
提示:以冰场中心为坐标原点,向东为x轴正方向,向北为y轴正方向,建立二维平面直角坐标系。
任务3.描述翱翔在蓝天上的飞机的位置,应该建立怎样的坐标系?
提示:确定一点(如机场所在位置)为坐标原点,建立三维空间直角坐标系。
为了定量研究物体的位置变化,我们可以用坐标轴(x轴)来表达。现在以广场中心为坐标原点,沿东西方向建立坐标轴,规定向西为正方向。优优小朋友在游玩时,坐标轴上标明了她在不同时刻的坐标值,如图所示,上午九时在A位置,九时十分在B位置。下列判断正确的是
A.九时,优优在广场中心东边2 m处
B.九时,优优在广场中心西边4 m处
C.九时十分,优优在广场中心东边4 m处
D.九时十分,优优在广场中心西边2 m处
例1
√
由题图可知,九时,优优小朋友在广场中心西边4 m处,A错误,B正确;九时十分,优优在广场中心东边2 m处,C、D错误。
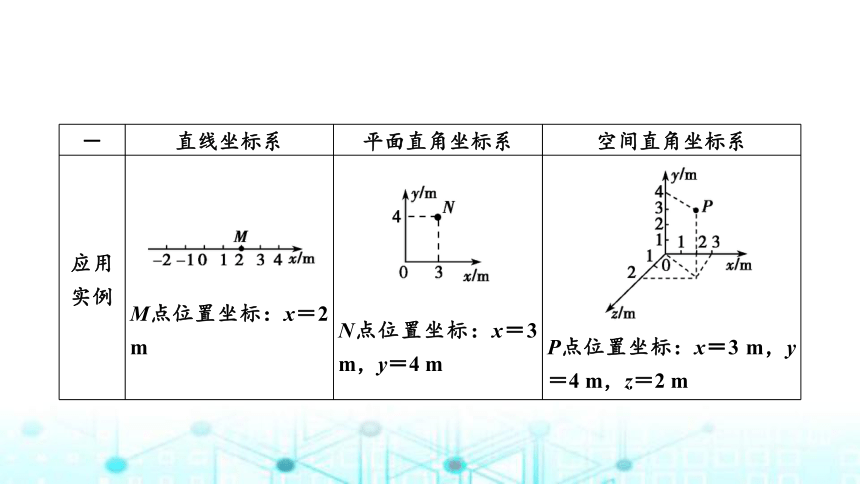
三种坐标系的比较
- 直线坐标系 平面直角坐标系 空间直角坐标系
适用
运动 物体沿直线运动时 物体在某平面内做运动时 物体在空间内做运动时
建立
方法 在直线上规定原点、正方向和标度,就建立了直线坐标系 在平面内画相互垂直的x轴与y轴,即可组成平面直角坐标系。物体的位置由一对坐标值确定 在空间画三个相互垂直的x轴、y轴和z轴,即可组成空间直角坐标系。物体的位置由三个坐标值来确定
- 直线坐标系 平面直角坐标系 空间直角坐标系
应用
实例
M点位置坐标:x=2 m
N点位置坐标:x=3 m,y=4 m
P点位置坐标:x=3 m,y=4 m,z=2 m
针对练1.以北京长安街为坐标轴x,向东为正方向,以天安门中心所对的长安街中心为坐标原点O,建立一维坐标系,一辆汽车在原点东边2 km处,如果将坐标原点向西移5 km,则移动前、后这辆汽车的位置坐标x1、x2分别是
A.x1=5 km、x2=7 km B.x1=2 km、x2=5 km
C.x1=2 km、x2=7 km D.x1=3 km、x2=5 km
√
移动坐标原点前,汽车在原点的东边,距原点2 km,坐标原点向西移5 km后,汽车还在原点东边,距原点7 km,故这辆汽车在坐标原点移动前、后的位置坐标分别是x1=2 km、x2=7 km,C正确。
针对练2.如图所示,某人从学校门口A处开始散步,先向南走50 m到达B处,再向东走100 m到达C处,最后又向北走150 m到达D处,若以校门口A点为坐标原点,则A、B、C、D各点的位置如何表示?
答案:见解析
返回
以A点为坐标原点,向东为x轴的正方向,向北为y轴的正方向建立平面直角坐标系,如图所示,则各点的位置坐标为A(0,0),B(0,-50 m),C(100 m,-50 m),D(100 m,100 m)。
知识点二 位置的改变——位移 矢量和标量
自主学习
情境导入 从北京去重庆有三种方式:乘火车,乘飞机,乘火车到武汉然后乘轮船沿长江而上。
(1)三种方式运动轨迹的长短相同吗?
提示:轨迹长短不同
(2)轨迹最短的是哪一种方案?
提示:乘飞机
(3)三种方式有什么共同之处吗?
提示:位置变化相同
教材梳理 (阅读教材P9—P12完成下列填空)
1.路程:物体运动路线的________。
2.位移
(1)定义:物理学中描述物体________变化的物理量。
(2)表示方法:常用由初位置指向末位置的____________来表示。
(3)方向:由初位置指向末位置。
(4)大小:有向线段的长短。
3.矢量和标量
(1)矢量:既有________又有________的物理量,如位移。
(2)标量:只有________没有________的物理量,如路程、温度等。
(3)运算法则:两个标量加减时遵循“____________”,矢量加减的法则与此不同。
长度
位置
有向线段
大小
方向
大小
方向
算术法则
课堂探究
师生互动 小明是一个象棋爱好者,在某次与棋友的对弈过程中,在三步棋里把自己的“車”从图中的A位置经过B位置、C位置最后移到了D位置。设象棋棋盘上相邻横线与纵线间的距离都等于a,则:
任务1.这三步棋里棋子的总路程是多少?
提示:5a+9a+2a=16a
任务2.从A到D,棋子的位移大小是多少?
提示: a
任务3.路程和位移的大小相等吗?
提示:不相等
角度1 路程和位移
(2024·云南曲靖高一上学期月考)如图所示,物体沿半径均为R的半圆弧AB和
圆弧BCDE从A运动到E,其中A、O1、B、O2、D在一条直线上,AB、BD和CE是直径,O1和O2是圆心,下列说法正确的是
例2
A.当物体运动到B点时,位移大小和路程都是2R
B.物体从A运动到C点和从A运动到E点位移相同
C.当物体运动到D点时,位移大小和路程都是4R
D.当物体运动到E点时,位移大小是 R,路程是2.5πR
√
路程是物体运动轨迹的长度,位移是由物体运动的初位置指向末位置的有向线段,当物
体运动到B点时,路程为 =πR,位移大小为2R,故A错误;物体从A运动到C点和从
A运动到E点位移大小均为 = R,方向分别为A→C与A→E,
即位移大小相等、方向不同,故B错误;当物体运动到D点时,位移大小
为4R,路程为 =2πR,故C错误;当物体运动到E点时,位移大小是 R,路程为 ×2πR=2.5πR,故D正确。
位移与路程的区别与联系
项目 位移 路程
区
别 物理意义 表示质点的位置变化 表示质点的运动轨迹
大小 从初位置到末位置的直线距离 运动轨迹的长度
方向 从初位置指向末位置 无方向
联系 (1)都是过程量,描述质点运动的空间特征
(2)一般来说,位移的大小要小于相应的路程,只有质点做单向直线运动时,位移的大小才等于路程
针对练1.如图所示,标准的排球比赛场地为长方形ABCD,其中AB=18 m,BC=9 m。某同学从A点起跑,沿着排球场的边缘,依次经过B点、C点、D点,最终回到A点。下列判断正确的是
A.该同学从A点到C点,位移大小是27 m
B.该同学从A点到D点,位移大小是9 m
C.该同学从A点到A点,路程是0
D.该同学从A点到D点和从D点到A点,位移相同
√
该同学从A点到C点,位移大小是xAC=
≈20.1 m,故A错误;该同学从A点到D点,位移大小是xAD=9 m,故B正确;该同学从A点到A点,路程是运动轨迹的长度,则s=2×(18+9) m=54 m,故C错误;该同学从A点到D点和从D点到A点,位移大小相等、方向不同,故D错误。
针对练2.(多选)某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1 m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是
A.质点在从A→B→C的过程中发生的位移为2 m,路程为4 m
B.质点在从B→D的过程中发生的位移为-4 m,路程为4 m
C.当质点到达D点时,其位置可用D点的坐标-2 m表示
D.当质点到达D点时,相对于A点的位移为-5 m
√
√
质点在从A→B→C的过程中,位移的大小为从A点指向C点的线段的长度,大小为2 m,方向为A到C,所以位移为-2 m,路程为4 m,A错误;质点在从B→D的过程中,经过的路程为4 m,位移方向由B指向D,所以位移为-4 m,B正确;当质点到达D点时,位置在原点的左侧,坐标为-2 m,在A点左侧3 m处,相对于A点的位移为-3 m,C正确,D错误。
角度2 矢量和标量
(多选)下列关于矢量(位移)和标量(温度)的说法正确的是
A.做直线运动的两物体位移x甲=3 m,x乙=-5 m,则乙的位移大于甲的位移
B.两运动物体的位移大小均为30 m,这两个位移一定相同
C.温度计读数有正有负,其正、负号表示方向
D.温度计读数t1=3 ℃,t2=-5 ℃,则t1>t2
例3
√
√
位移的符号只代表方向,不代表大小,做直线运动的两物体位移x甲=3 m,x乙=-5 m,则乙的位移大于甲的位移,A正确;两运动物体的位移大小均为30 m,但是方向不一定相同,则这两个位移不一定相同,B错误;温度计读数有正有负,其正、负号并不表示方向,而是代表温度的高低,温度计读数t1=3 ℃,t2=-5 ℃,则t1>t2,C错误,D正确。
矢量的三点理解
1.矢量是有方向的,标量是没有方向的。
2.标量的运算法则为算术运算法则,即加、减、乘、除等运算方法;矢量的运算法则为以后要学到的平行四边形定则。
3.矢量大小的比较要看其数值的绝对值大小,绝对值大的矢量大,其“+”“-”号只代表方向。
返回
知识点三 位移—时间图像
自主学习
情境导入 a、b两物体都在做匀速直线运动,它们运动的位置、时刻信息如下表所示:
位置 时刻
0 2 s 4 s 6 s
a物体的位置xa 0 1 m 2 m 3 m
b物体的位置xb 4 m 2 m 0 -2 m
(1)a、b两物体沿x轴正方向还是x轴负方向运动?
提示:由于a的位置坐标随时间在增大,说明a沿x轴正方向运动;b的位置坐标随时间在减小,说明b沿x轴负方向运动。
(2)试以时刻t为横轴,以位置坐标x为纵轴,建立直角坐标系,在坐标系中将a、b两物体的时刻、位置信息描点,并按照各点排列趋势用平滑的曲线连接起来。
提示:
位置 时刻
0 2 s 4 s 6 s
a物体的位置xa 0 1 m 2 m 3 m
b物体的位置xb 4 m 2 m 0 -2 m
教材梳理 (阅读教材P11完成下列填空)
1.x-t图像
(1)原点O表示运动的起始________和起始________。
(2)横轴表示时间,纵轴表示位移。
2.意义:能较直观地看出物体运动过程中位置的变化。x-t图像描述物体位置随时间变化的规律特征,并不是物体运动的轨迹。
位置
时刻
课堂探究
师生互动 有一天,兔子和乌龟赛跑。兔子认为赢乌龟太轻松了,决定途中先打个盹,再追上乌龟。乌龟一刻不停地努力向前爬,当兔子醒来的时候,乌龟已经远远超过了兔子。如图是“龟兔赛跑”的x-t图像。
任务1.哪一条表示乌龟的运动图线?哪一条表示兔子的运动图线?
提示:由题意可知,图线OBCE表示乌龟的运动图线,图线OABDF表示兔子的运动图线。
任务2.兔子从什么时候在什么位置开始睡觉?在什么时候乌龟爬过兔子身旁?
提示:兔子从t1时刻、距出发点x1的位置开始睡觉。在t2时刻乌龟悄悄地爬过兔子身旁。
任务3.兔子睡了多长时间?兔子醒来时乌龟在什么地方?谁先到达终点?提前多少时间到达?
提示:兔子睡觉的时间是从t1到t3,时间为t3-t1。当兔子醒来时乌龟在离出发点x2的地方。乌龟先到达终点,兔子后到达终点,提前到达的时间为t5-t4。
任务4.x-t图线是否表示兔子和乌龟的运动轨迹?
提示:不是。x-t图线表示位置随时间的变化情况。
(多选)关于如图所示的数据,下列说法中正确的是
A.物体在第1 s内的位移为4 m
B.物体在第5 s内的位移为8 m
C.物体在前5 s内的位移为8 m
D.物体在后5 s内的位移为16 m
例4
√
√
由题图可知,物体在0~2 s内位移从0均匀增加到8 m,即每秒钟发生的位移是4 m,A正确;物体在第5 s内是静止的,位移为零,B错误;物体在前5 s内的位移即为前2 s内的位移,等于8 m,C正确;物体在后5 s内的位移为6~10 s的位移,等于8 m,D错误。
1.从x-t图像能获得的信息
(1)判断质点是静止的还是运动的。
(2)判断质点运动过程中是离出发点越来越远,还是越来越近。
(3)任意时间内质点运动的位移。
(4)质点发生某段位移所用的时间。
(5)图像不过原点,说明开始计时时质点的位置不为零,或经过一段时间才开始运动。
(6)两图线相交,表示两质点在这一时刻位于同一位置(相遇)。
2.常见的几种x-t图像的比较
图像 物理意义
①、②都表示物体处于静止状态,但静止的位置不同
③表示物体从x1处沿正方向做直线运动
④表示物体从x=0处沿正方向做直线运动
⑤表示物体从x2处沿负方向做直线运动
针对练1.(多选)如图为A、B两个物体从O点开始运动的位移—时间图像的一部分。从A、B两物体的位移—时间图像可知,下列说法中正确的是
A.A、B两物体的运动方向相同
B.A物体4 s内发生的位移是10 m
C.B物体发生10 m位移的时间是4 s
D.A、B两物体同时开始运动
√
√
√
A、B两物体运动的x-t图线相对时间轴的倾斜方向相同,即A、B两物体的运动方向相同,选项A正确;由题图可知,B物体在4 s内的位移是10 m,A物体在2 s内的位移为10 m,选项B错误,C正确;A、B两物体都是从0时刻开始运动,选项D正确。
针对练2.甲、乙、丙三个物体同时同地出发,6 s末同时到达同一目的地,它们运动的位移—时间图像如图所示,则关于三者的路程s和位移大小x的关系,正确的是
A.s甲>s丙=s乙 B.s甲>s丙>s乙
C.x甲>x丙>x乙 D.x甲=x丙>x乙
√
甲、乙、丙三者均做直线运动,由于三者的初、末位置均相同,故位移相同,即x甲=x乙=x丙;由题图可知,甲物体有反向运动过程,而乙、丙均只有单向运动,即乙、丙的路程等于位移大小,而甲的路程大于位移大小,则s甲>s乙=s丙,故选A。
返回
随堂演练
1.(鲁科版教材P23T5改编)一小球沿斜面向上运动了5 m,接着沿斜面向下运动了8 m,在整个过程中,该小球的位移大小是
A.13 m B.8 m
C.5 m D.3 m
√
设沿斜面向上为正方向,则小球沿斜面向上运动的位移为5 m,向下运动的位移为-8 m,全程的位移为x=-8 m+5 m=-3 m,负号表示方向沿斜面向下,即大小为3 m。
2.(多选)(2023·河南商丘期中)如图,运动员在400 m标准田径场的跑道上进行比赛,下列说法正确的是
A.400 m比赛,外跑道上的运动员的路程大
B.400 m比赛,不同跑道上的运动员的路程相同
C.400 m比赛,不同跑道上的运动员的位移相同
D.100 m比赛在直道上进行,运动员的位移大小与路程相等
√
√
路程是物体运动轨迹的长度,400 m比赛,不同跑道上的运动员的路程相同,故A错误,B正确;400 m比赛,不同跑道上的运动员起点不同,终点相同,不同跑道上的运动员的位移不同,故C错误;100 m比赛在直道上进行,运动员的位移大小与路程相等,故D正确。故选BD。
3.(人教版教材P20T5改编)(多选)一辆汽车在教练场上沿平直道路行驶,以x表示它相对于出发点的位移。图中近似描写了汽车在0时刻到40 s这段时间的x-t图像,则下列说法正确的是
A.汽车在0~10 s时间内驶离出发点
B.汽车在10 ~20 s时间内没有行驶
C.汽车在20 ~40 s时间内驶离出发点
D.在40 s时汽车离出发点最远
√
√
由题图可知,在0~10 s时间内,汽车离出发点越来越远,A正确;在10 ~20 s时间内,汽车离出发点的距离是30 m,汽车没有行驶,B正确;在20 ~40 s时间内,汽车离出发点越来越近,C错误;在40 s时汽车回到出发点,D错误。
4.(鲁科版教材P33T4)如图所示,一摩天轮的半径为R,轮缘上的座舱随轮转动。若转动一周,求:
(1)座舱的位移和路程;
答案:0 2πR
座舱转动一周,其位移为0,路程为s=2πR。
(2)转动过程中,座舱的最大位移和最大路程。
答案:2R 2πR
座舱转动一周,最大位移为2R,最大路程为2πR。
返回
课 时 测 评
1.(2024·四川内江高一期末)对沿直线运动的物体,下列说法中正确的是
A.若物体沿直线一直向某一方向(单方向)运动,物体运动的路程就是位移
B.若物体运动的路程不为零,则位移也一定不为零
C.若物体的位移为零,则通过的路程也一定为零
D.若物体通过的路程不为零,但位移有可能为零
√
若物体沿直线一直向某一方向(单方向)运动,物体运动的路程与位移大小相等,但不能说路程就是位移,故A错误;若物体运动的路程不为零,则位移可能为零,如做往返运动的物体回到出发点时,路程不为零,但是位移为零,故B、C错误,D正确。
2.有一口井,水面距井口4 m,现用水桶从井中提水(如图所示),水桶出井后又将其提升了1 m,选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时和最后的位置坐标分别是
A.4 m,5 m
B.5 m,0
C.-4 m,1 m
D.-5 m,1 m
√
水桶在水面时与井口的距离为4 m,位于井口的下方,坐标为x=-4 m,而最后的位置与井口的距离为1 m,位于井口的上方,坐标为x=1 m,故C正确。
3.如图甲为中国“玉兔”月球车在月球上巡视勘察的情景。若以着陆点为坐标原点建立直角坐标系,如图乙所示,A、B是两个要探测的点。“玉兔”从原点出发,先沿x轴正方向行驶,运动到离A点最近的位置坐标为x1;再转弯沿y轴正方向行驶,经过A点后继续沿y轴正方向行驶,运动到离B点最近的位置坐标为y1,则x1、y1的值为
A.2,2
B.7,4
C.2,4
D.4,7
√
由题图可知,“玉兔”从(0,0)沿x轴正方向出发,到(2 km,0)转弯,向y轴正方向运动,到(2 km,4 km)时离B点最近,所以C正确。
4.(2024·衢州高级中学高一期中)如图所示,“天舟二号”货运飞船与空间站在交会对接之前,分别沿半径为r、R的圆形轨道运动。某时刻“天舟二号”货运飞船和空间站分别从B点、A点开始运动,下列说法正确的是
A.空间站运行一周的位移大小为2πR
B.“天舟二号”运行 周的路程为2r
C.“天舟二号”运行 周的位移大小为 r
D.二者各自运行一周,其路程相等
√
空间站运行一周的位移为0,A错误;“天舟二号”运行 周的路程为πr,B错误;“天舟二号”运行 周的位移大小为 r,C正确;“天舟二号”和空间站各自运行一周,其路程分别为2πr和2πR,路程不相等,D错误。
5.(2024·山东滨州期中)如图所示,一遥控玩具小车在xOy平面内运动,它从坐标原点O出发,先以4 m/s的速度沿x轴正方向运动100 s,接着以3 m/s的速度沿y轴正方向运动200 s,最后以2 m/s的速度沿x轴正方向运动200 s,则遥控玩具小车在整个运动过程中的位移和路程的大小分别为
A.1 000 m、1 000 m
B.1 400 m、1 400 m
C.1 000 m、1 400 m
D.1 400 m、1 000 m
√
由匀速直线运动规律x=vt,可得遥控玩具小车在各个时间段内的位移为x1=4×100 m=400 m,x2=3×200 m=600 m,x3=2×200 m=400 m,位移是矢量,是指从初位置指向末位置的有向线段,则位移为x=
m=1 000 m,路程是实际走过的轨迹长度,故路程为s=400 m+400 m+600 m=1 400 m,故C正确。
6.(2024·广东广州期中)天和核心舱是中国空间站发射入轨的首个舱段,主要用于空间站统一控制和管理,备具长期自主飞行能力。天和核心舱绕地球运动时可视为质点,轨迹是半径为r的圆,核心舱从起点A绕一圈回到A的过程中最大的位移是
A.0
B.2r
C.2πr
D.πr
√
当核心舱从A运动至与A关于圆心O对称的位置时位移最大,为2r,故B正确。
7.某一质点做直线运动的位移x和时间t的关系图像如图所示,那么该质点在3 s内通过的路程和位移大小分别为
A.6 m和1 m
B.5 m和1 m
C.5 m和5 m
D.1 m和1 m
√
由位移x和时间t的关系图像可知,0~1 s内,质点静止在x1=3 m处,1~2 s内质点沿反方向运动,且t=2 s时,质点运动至x2=2 m处,并且最后1 s 静止在该处,所以整个过程中质点运动的路程和位移大小相等,均为1 m,选项D正确。
8.(多选)下列关于矢量(位移)和标量(温度)的说法中,正确的是
A.两运动物体的位移大小均为30 m,这两个位移不一定相同
B.做直线运动的两物体的位移x甲=3 m,x乙=-5 m,则x甲>x乙
C.温度计读数有正有负,其正负号表示温度方向
D.温度计读数的正负号表示温度的高低
√
√
两物体的位移大小虽然均为30 m,但由于不知其方向关系,两个位移不一定相同,A正确;比较物体位移大小应比较其绝对值,B错误;温度无方向,其正负表示温度的高低,C错误,D正确。
9.(2024·陕西安康高一校联考期末)如图所示,自行车的车轮半径为R,车轮沿直线无滑动地滚动,当气门芯由轮子的正上方第一次运动到轮子正下方时,气门芯位移的大小为
A.πR B.2R
C.2πR D. R
√
当气门芯由轮子的正上方第一次运动到轮子正下方时轮子向前运动半个周长,气门芯在水平方向上移动的距离为πR,在竖直方向上移动的距离为2R,由勾股定理可知,气门芯位移的大小为
R。
10.如图为A、B两人在同一直线上运动的位移—时间图像,下列分析正确的是
A.0~2 s内,A、B两人同向而行
B.0~2 s内,A单位时间内的位移比B的大
C.前5 s内,A的路程比B的路程小
D.前5 s内,A的位移比B的位移小
√
由位移—时间图像可以看出,0~2 s内,A沿负方向运动,B沿正方向运动,两人运动方向相反,故A错误;0~2 s内,A的位移为-24 m,单位时间(每秒)内的位移为-12 m;B的位移为60 m,单位时间(每秒)内的位移为30 m,正负
号表示方向,故B错误;前5 s内,B正向运动60 m,静止2 s后又负向运动30 m,即B的路程为90 m;A的路程为60 m,故A的路程比B的路程小,故C正确;前5 s内,A的位移大小为60 m,B的位移大小为30 m,故A的位移大于B的位移,故D错误。
11.(10分)某班级的教室在3楼,每天同学们都要从1楼爬到3楼上课。如图所示,若每层楼的高度都是3 m,楼梯的倾角为45°,某同学从楼梯沿折线从大门走到3楼教室门口,他走过的位移大小是多少?路程是多少?(把某同学爬楼过程等效为物体沿坡滑行)
答案:6 m 6 m
由题图可知,折线为某同学的运动轨迹,每个斜梯长为1.5 m,
路程l=4×1.5 m=6 m。
初位置在大门口,末位置在教室门口,从初位置到末位置的有向线段为位移,所以位移大小为x=2h=6 m。
12.(10分)如图所示,实心长方体木块ABCD-A′B′C′D′的长、宽、高分别为a、b、c,且a>b>c。有一个小虫自A′点运动到C点,求:
(1)小虫的位移大小;
答案:
小虫的位移大小为由A′指向C的有向线段的长度,为x=
(2)小虫的最小路程。
答案:
小虫的最小路程应等于将ABCD-A′B′C′D′展开后A′C之间的连线长度,
返回
2.位置 位移
第一章 描述运动的基本概念
1.会选择坐标系描述位置。
2.理解位移的概念,会区分位移和路程的不同。
3.理解位移—时间图像的意义。
素养目标
知识点一 确定质点位置的方法——坐标系
自主学习
情境导入 某段平直公路沿线每隔1 km设置一块用以指示相对起点的里程碑。
(1)如果以某一里程碑为起点,司机能不能确定在某段时间内所走的距离?
提示:能
(2)如果以某一里程碑为起点,以司机行驶的方向为正方向,是否能看成数轴?
提示:能
教材梳理 (阅读教材P7—P8完成下列填空)
1.坐标系及坐标
要准确地描述质点的位置,需要建立__________,即按照规定的方法选取一组________的数来描述它的________,这组有序的数就是“坐标”。
2.坐标系的种类
(1)一维坐标系:物体沿一条直线运动,要准确描述物体的位置需建立____________坐标系。
(2)二维坐标系:确定地球表面物体的位置常用的坐标系是经纬度,它是固定在地球表面上的二维平面直角坐标系。
(3)三维坐标系:像空中飞行的物体,要准确描述其位置,除经纬度外,还需要高度的数值,这就是三维空间直角坐标系。
坐标系
有序
位置
一维直线
课堂探究
师生互动 观察下列三种运动情景,回答下列问题:
任务1.描述百米赛跑运动员在运动中的位置,应该建立怎样的坐标系?
提示:以起点为坐标原点,建立一维直线坐标系。
任务2.描述冰场上花样滑冰运动员的位置,应该建立怎样的坐标系?
提示:以冰场中心为坐标原点,向东为x轴正方向,向北为y轴正方向,建立二维平面直角坐标系。
任务3.描述翱翔在蓝天上的飞机的位置,应该建立怎样的坐标系?
提示:确定一点(如机场所在位置)为坐标原点,建立三维空间直角坐标系。
为了定量研究物体的位置变化,我们可以用坐标轴(x轴)来表达。现在以广场中心为坐标原点,沿东西方向建立坐标轴,规定向西为正方向。优优小朋友在游玩时,坐标轴上标明了她在不同时刻的坐标值,如图所示,上午九时在A位置,九时十分在B位置。下列判断正确的是
A.九时,优优在广场中心东边2 m处
B.九时,优优在广场中心西边4 m处
C.九时十分,优优在广场中心东边4 m处
D.九时十分,优优在广场中心西边2 m处
例1
√
由题图可知,九时,优优小朋友在广场中心西边4 m处,A错误,B正确;九时十分,优优在广场中心东边2 m处,C、D错误。
三种坐标系的比较
- 直线坐标系 平面直角坐标系 空间直角坐标系
适用
运动 物体沿直线运动时 物体在某平面内做运动时 物体在空间内做运动时
建立
方法 在直线上规定原点、正方向和标度,就建立了直线坐标系 在平面内画相互垂直的x轴与y轴,即可组成平面直角坐标系。物体的位置由一对坐标值确定 在空间画三个相互垂直的x轴、y轴和z轴,即可组成空间直角坐标系。物体的位置由三个坐标值来确定
- 直线坐标系 平面直角坐标系 空间直角坐标系
应用
实例
M点位置坐标:x=2 m
N点位置坐标:x=3 m,y=4 m
P点位置坐标:x=3 m,y=4 m,z=2 m
针对练1.以北京长安街为坐标轴x,向东为正方向,以天安门中心所对的长安街中心为坐标原点O,建立一维坐标系,一辆汽车在原点东边2 km处,如果将坐标原点向西移5 km,则移动前、后这辆汽车的位置坐标x1、x2分别是
A.x1=5 km、x2=7 km B.x1=2 km、x2=5 km
C.x1=2 km、x2=7 km D.x1=3 km、x2=5 km
√
移动坐标原点前,汽车在原点的东边,距原点2 km,坐标原点向西移5 km后,汽车还在原点东边,距原点7 km,故这辆汽车在坐标原点移动前、后的位置坐标分别是x1=2 km、x2=7 km,C正确。
针对练2.如图所示,某人从学校门口A处开始散步,先向南走50 m到达B处,再向东走100 m到达C处,最后又向北走150 m到达D处,若以校门口A点为坐标原点,则A、B、C、D各点的位置如何表示?
答案:见解析
返回
以A点为坐标原点,向东为x轴的正方向,向北为y轴的正方向建立平面直角坐标系,如图所示,则各点的位置坐标为A(0,0),B(0,-50 m),C(100 m,-50 m),D(100 m,100 m)。
知识点二 位置的改变——位移 矢量和标量
自主学习
情境导入 从北京去重庆有三种方式:乘火车,乘飞机,乘火车到武汉然后乘轮船沿长江而上。
(1)三种方式运动轨迹的长短相同吗?
提示:轨迹长短不同
(2)轨迹最短的是哪一种方案?
提示:乘飞机
(3)三种方式有什么共同之处吗?
提示:位置变化相同
教材梳理 (阅读教材P9—P12完成下列填空)
1.路程:物体运动路线的________。
2.位移
(1)定义:物理学中描述物体________变化的物理量。
(2)表示方法:常用由初位置指向末位置的____________来表示。
(3)方向:由初位置指向末位置。
(4)大小:有向线段的长短。
3.矢量和标量
(1)矢量:既有________又有________的物理量,如位移。
(2)标量:只有________没有________的物理量,如路程、温度等。
(3)运算法则:两个标量加减时遵循“____________”,矢量加减的法则与此不同。
长度
位置
有向线段
大小
方向
大小
方向
算术法则
课堂探究
师生互动 小明是一个象棋爱好者,在某次与棋友的对弈过程中,在三步棋里把自己的“車”从图中的A位置经过B位置、C位置最后移到了D位置。设象棋棋盘上相邻横线与纵线间的距离都等于a,则:
任务1.这三步棋里棋子的总路程是多少?
提示:5a+9a+2a=16a
任务2.从A到D,棋子的位移大小是多少?
提示: a
任务3.路程和位移的大小相等吗?
提示:不相等
角度1 路程和位移
(2024·云南曲靖高一上学期月考)如图所示,物体沿半径均为R的半圆弧AB和
圆弧BCDE从A运动到E,其中A、O1、B、O2、D在一条直线上,AB、BD和CE是直径,O1和O2是圆心,下列说法正确的是
例2
A.当物体运动到B点时,位移大小和路程都是2R
B.物体从A运动到C点和从A运动到E点位移相同
C.当物体运动到D点时,位移大小和路程都是4R
D.当物体运动到E点时,位移大小是 R,路程是2.5πR
√
路程是物体运动轨迹的长度,位移是由物体运动的初位置指向末位置的有向线段,当物
体运动到B点时,路程为 =πR,位移大小为2R,故A错误;物体从A运动到C点和从
A运动到E点位移大小均为 = R,方向分别为A→C与A→E,
即位移大小相等、方向不同,故B错误;当物体运动到D点时,位移大小
为4R,路程为 =2πR,故C错误;当物体运动到E点时,位移大小是 R,路程为 ×2πR=2.5πR,故D正确。
位移与路程的区别与联系
项目 位移 路程
区
别 物理意义 表示质点的位置变化 表示质点的运动轨迹
大小 从初位置到末位置的直线距离 运动轨迹的长度
方向 从初位置指向末位置 无方向
联系 (1)都是过程量,描述质点运动的空间特征
(2)一般来说,位移的大小要小于相应的路程,只有质点做单向直线运动时,位移的大小才等于路程
针对练1.如图所示,标准的排球比赛场地为长方形ABCD,其中AB=18 m,BC=9 m。某同学从A点起跑,沿着排球场的边缘,依次经过B点、C点、D点,最终回到A点。下列判断正确的是
A.该同学从A点到C点,位移大小是27 m
B.该同学从A点到D点,位移大小是9 m
C.该同学从A点到A点,路程是0
D.该同学从A点到D点和从D点到A点,位移相同
√
该同学从A点到C点,位移大小是xAC=
≈20.1 m,故A错误;该同学从A点到D点,位移大小是xAD=9 m,故B正确;该同学从A点到A点,路程是运动轨迹的长度,则s=2×(18+9) m=54 m,故C错误;该同学从A点到D点和从D点到A点,位移大小相等、方向不同,故D错误。
针对练2.(多选)某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1 m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是
A.质点在从A→B→C的过程中发生的位移为2 m,路程为4 m
B.质点在从B→D的过程中发生的位移为-4 m,路程为4 m
C.当质点到达D点时,其位置可用D点的坐标-2 m表示
D.当质点到达D点时,相对于A点的位移为-5 m
√
√
质点在从A→B→C的过程中,位移的大小为从A点指向C点的线段的长度,大小为2 m,方向为A到C,所以位移为-2 m,路程为4 m,A错误;质点在从B→D的过程中,经过的路程为4 m,位移方向由B指向D,所以位移为-4 m,B正确;当质点到达D点时,位置在原点的左侧,坐标为-2 m,在A点左侧3 m处,相对于A点的位移为-3 m,C正确,D错误。
角度2 矢量和标量
(多选)下列关于矢量(位移)和标量(温度)的说法正确的是
A.做直线运动的两物体位移x甲=3 m,x乙=-5 m,则乙的位移大于甲的位移
B.两运动物体的位移大小均为30 m,这两个位移一定相同
C.温度计读数有正有负,其正、负号表示方向
D.温度计读数t1=3 ℃,t2=-5 ℃,则t1>t2
例3
√
√
位移的符号只代表方向,不代表大小,做直线运动的两物体位移x甲=3 m,x乙=-5 m,则乙的位移大于甲的位移,A正确;两运动物体的位移大小均为30 m,但是方向不一定相同,则这两个位移不一定相同,B错误;温度计读数有正有负,其正、负号并不表示方向,而是代表温度的高低,温度计读数t1=3 ℃,t2=-5 ℃,则t1>t2,C错误,D正确。
矢量的三点理解
1.矢量是有方向的,标量是没有方向的。
2.标量的运算法则为算术运算法则,即加、减、乘、除等运算方法;矢量的运算法则为以后要学到的平行四边形定则。
3.矢量大小的比较要看其数值的绝对值大小,绝对值大的矢量大,其“+”“-”号只代表方向。
返回
知识点三 位移—时间图像
自主学习
情境导入 a、b两物体都在做匀速直线运动,它们运动的位置、时刻信息如下表所示:
位置 时刻
0 2 s 4 s 6 s
a物体的位置xa 0 1 m 2 m 3 m
b物体的位置xb 4 m 2 m 0 -2 m
(1)a、b两物体沿x轴正方向还是x轴负方向运动?
提示:由于a的位置坐标随时间在增大,说明a沿x轴正方向运动;b的位置坐标随时间在减小,说明b沿x轴负方向运动。
(2)试以时刻t为横轴,以位置坐标x为纵轴,建立直角坐标系,在坐标系中将a、b两物体的时刻、位置信息描点,并按照各点排列趋势用平滑的曲线连接起来。
提示:
位置 时刻
0 2 s 4 s 6 s
a物体的位置xa 0 1 m 2 m 3 m
b物体的位置xb 4 m 2 m 0 -2 m
教材梳理 (阅读教材P11完成下列填空)
1.x-t图像
(1)原点O表示运动的起始________和起始________。
(2)横轴表示时间,纵轴表示位移。
2.意义:能较直观地看出物体运动过程中位置的变化。x-t图像描述物体位置随时间变化的规律特征,并不是物体运动的轨迹。
位置
时刻
课堂探究
师生互动 有一天,兔子和乌龟赛跑。兔子认为赢乌龟太轻松了,决定途中先打个盹,再追上乌龟。乌龟一刻不停地努力向前爬,当兔子醒来的时候,乌龟已经远远超过了兔子。如图是“龟兔赛跑”的x-t图像。
任务1.哪一条表示乌龟的运动图线?哪一条表示兔子的运动图线?
提示:由题意可知,图线OBCE表示乌龟的运动图线,图线OABDF表示兔子的运动图线。
任务2.兔子从什么时候在什么位置开始睡觉?在什么时候乌龟爬过兔子身旁?
提示:兔子从t1时刻、距出发点x1的位置开始睡觉。在t2时刻乌龟悄悄地爬过兔子身旁。
任务3.兔子睡了多长时间?兔子醒来时乌龟在什么地方?谁先到达终点?提前多少时间到达?
提示:兔子睡觉的时间是从t1到t3,时间为t3-t1。当兔子醒来时乌龟在离出发点x2的地方。乌龟先到达终点,兔子后到达终点,提前到达的时间为t5-t4。
任务4.x-t图线是否表示兔子和乌龟的运动轨迹?
提示:不是。x-t图线表示位置随时间的变化情况。
(多选)关于如图所示的数据,下列说法中正确的是
A.物体在第1 s内的位移为4 m
B.物体在第5 s内的位移为8 m
C.物体在前5 s内的位移为8 m
D.物体在后5 s内的位移为16 m
例4
√
√
由题图可知,物体在0~2 s内位移从0均匀增加到8 m,即每秒钟发生的位移是4 m,A正确;物体在第5 s内是静止的,位移为零,B错误;物体在前5 s内的位移即为前2 s内的位移,等于8 m,C正确;物体在后5 s内的位移为6~10 s的位移,等于8 m,D错误。
1.从x-t图像能获得的信息
(1)判断质点是静止的还是运动的。
(2)判断质点运动过程中是离出发点越来越远,还是越来越近。
(3)任意时间内质点运动的位移。
(4)质点发生某段位移所用的时间。
(5)图像不过原点,说明开始计时时质点的位置不为零,或经过一段时间才开始运动。
(6)两图线相交,表示两质点在这一时刻位于同一位置(相遇)。
2.常见的几种x-t图像的比较
图像 物理意义
①、②都表示物体处于静止状态,但静止的位置不同
③表示物体从x1处沿正方向做直线运动
④表示物体从x=0处沿正方向做直线运动
⑤表示物体从x2处沿负方向做直线运动
针对练1.(多选)如图为A、B两个物体从O点开始运动的位移—时间图像的一部分。从A、B两物体的位移—时间图像可知,下列说法中正确的是
A.A、B两物体的运动方向相同
B.A物体4 s内发生的位移是10 m
C.B物体发生10 m位移的时间是4 s
D.A、B两物体同时开始运动
√
√
√
A、B两物体运动的x-t图线相对时间轴的倾斜方向相同,即A、B两物体的运动方向相同,选项A正确;由题图可知,B物体在4 s内的位移是10 m,A物体在2 s内的位移为10 m,选项B错误,C正确;A、B两物体都是从0时刻开始运动,选项D正确。
针对练2.甲、乙、丙三个物体同时同地出发,6 s末同时到达同一目的地,它们运动的位移—时间图像如图所示,则关于三者的路程s和位移大小x的关系,正确的是
A.s甲>s丙=s乙 B.s甲>s丙>s乙
C.x甲>x丙>x乙 D.x甲=x丙>x乙
√
甲、乙、丙三者均做直线运动,由于三者的初、末位置均相同,故位移相同,即x甲=x乙=x丙;由题图可知,甲物体有反向运动过程,而乙、丙均只有单向运动,即乙、丙的路程等于位移大小,而甲的路程大于位移大小,则s甲>s乙=s丙,故选A。
返回
随堂演练
1.(鲁科版教材P23T5改编)一小球沿斜面向上运动了5 m,接着沿斜面向下运动了8 m,在整个过程中,该小球的位移大小是
A.13 m B.8 m
C.5 m D.3 m
√
设沿斜面向上为正方向,则小球沿斜面向上运动的位移为5 m,向下运动的位移为-8 m,全程的位移为x=-8 m+5 m=-3 m,负号表示方向沿斜面向下,即大小为3 m。
2.(多选)(2023·河南商丘期中)如图,运动员在400 m标准田径场的跑道上进行比赛,下列说法正确的是
A.400 m比赛,外跑道上的运动员的路程大
B.400 m比赛,不同跑道上的运动员的路程相同
C.400 m比赛,不同跑道上的运动员的位移相同
D.100 m比赛在直道上进行,运动员的位移大小与路程相等
√
√
路程是物体运动轨迹的长度,400 m比赛,不同跑道上的运动员的路程相同,故A错误,B正确;400 m比赛,不同跑道上的运动员起点不同,终点相同,不同跑道上的运动员的位移不同,故C错误;100 m比赛在直道上进行,运动员的位移大小与路程相等,故D正确。故选BD。
3.(人教版教材P20T5改编)(多选)一辆汽车在教练场上沿平直道路行驶,以x表示它相对于出发点的位移。图中近似描写了汽车在0时刻到40 s这段时间的x-t图像,则下列说法正确的是
A.汽车在0~10 s时间内驶离出发点
B.汽车在10 ~20 s时间内没有行驶
C.汽车在20 ~40 s时间内驶离出发点
D.在40 s时汽车离出发点最远
√
√
由题图可知,在0~10 s时间内,汽车离出发点越来越远,A正确;在10 ~20 s时间内,汽车离出发点的距离是30 m,汽车没有行驶,B正确;在20 ~40 s时间内,汽车离出发点越来越近,C错误;在40 s时汽车回到出发点,D错误。
4.(鲁科版教材P33T4)如图所示,一摩天轮的半径为R,轮缘上的座舱随轮转动。若转动一周,求:
(1)座舱的位移和路程;
答案:0 2πR
座舱转动一周,其位移为0,路程为s=2πR。
(2)转动过程中,座舱的最大位移和最大路程。
答案:2R 2πR
座舱转动一周,最大位移为2R,最大路程为2πR。
返回
课 时 测 评
1.(2024·四川内江高一期末)对沿直线运动的物体,下列说法中正确的是
A.若物体沿直线一直向某一方向(单方向)运动,物体运动的路程就是位移
B.若物体运动的路程不为零,则位移也一定不为零
C.若物体的位移为零,则通过的路程也一定为零
D.若物体通过的路程不为零,但位移有可能为零
√
若物体沿直线一直向某一方向(单方向)运动,物体运动的路程与位移大小相等,但不能说路程就是位移,故A错误;若物体运动的路程不为零,则位移可能为零,如做往返运动的物体回到出发点时,路程不为零,但是位移为零,故B、C错误,D正确。
2.有一口井,水面距井口4 m,现用水桶从井中提水(如图所示),水桶出井后又将其提升了1 m,选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时和最后的位置坐标分别是
A.4 m,5 m
B.5 m,0
C.-4 m,1 m
D.-5 m,1 m
√
水桶在水面时与井口的距离为4 m,位于井口的下方,坐标为x=-4 m,而最后的位置与井口的距离为1 m,位于井口的上方,坐标为x=1 m,故C正确。
3.如图甲为中国“玉兔”月球车在月球上巡视勘察的情景。若以着陆点为坐标原点建立直角坐标系,如图乙所示,A、B是两个要探测的点。“玉兔”从原点出发,先沿x轴正方向行驶,运动到离A点最近的位置坐标为x1;再转弯沿y轴正方向行驶,经过A点后继续沿y轴正方向行驶,运动到离B点最近的位置坐标为y1,则x1、y1的值为
A.2,2
B.7,4
C.2,4
D.4,7
√
由题图可知,“玉兔”从(0,0)沿x轴正方向出发,到(2 km,0)转弯,向y轴正方向运动,到(2 km,4 km)时离B点最近,所以C正确。
4.(2024·衢州高级中学高一期中)如图所示,“天舟二号”货运飞船与空间站在交会对接之前,分别沿半径为r、R的圆形轨道运动。某时刻“天舟二号”货运飞船和空间站分别从B点、A点开始运动,下列说法正确的是
A.空间站运行一周的位移大小为2πR
B.“天舟二号”运行 周的路程为2r
C.“天舟二号”运行 周的位移大小为 r
D.二者各自运行一周,其路程相等
√
空间站运行一周的位移为0,A错误;“天舟二号”运行 周的路程为πr,B错误;“天舟二号”运行 周的位移大小为 r,C正确;“天舟二号”和空间站各自运行一周,其路程分别为2πr和2πR,路程不相等,D错误。
5.(2024·山东滨州期中)如图所示,一遥控玩具小车在xOy平面内运动,它从坐标原点O出发,先以4 m/s的速度沿x轴正方向运动100 s,接着以3 m/s的速度沿y轴正方向运动200 s,最后以2 m/s的速度沿x轴正方向运动200 s,则遥控玩具小车在整个运动过程中的位移和路程的大小分别为
A.1 000 m、1 000 m
B.1 400 m、1 400 m
C.1 000 m、1 400 m
D.1 400 m、1 000 m
√
由匀速直线运动规律x=vt,可得遥控玩具小车在各个时间段内的位移为x1=4×100 m=400 m,x2=3×200 m=600 m,x3=2×200 m=400 m,位移是矢量,是指从初位置指向末位置的有向线段,则位移为x=
m=1 000 m,路程是实际走过的轨迹长度,故路程为s=400 m+400 m+600 m=1 400 m,故C正确。
6.(2024·广东广州期中)天和核心舱是中国空间站发射入轨的首个舱段,主要用于空间站统一控制和管理,备具长期自主飞行能力。天和核心舱绕地球运动时可视为质点,轨迹是半径为r的圆,核心舱从起点A绕一圈回到A的过程中最大的位移是
A.0
B.2r
C.2πr
D.πr
√
当核心舱从A运动至与A关于圆心O对称的位置时位移最大,为2r,故B正确。
7.某一质点做直线运动的位移x和时间t的关系图像如图所示,那么该质点在3 s内通过的路程和位移大小分别为
A.6 m和1 m
B.5 m和1 m
C.5 m和5 m
D.1 m和1 m
√
由位移x和时间t的关系图像可知,0~1 s内,质点静止在x1=3 m处,1~2 s内质点沿反方向运动,且t=2 s时,质点运动至x2=2 m处,并且最后1 s 静止在该处,所以整个过程中质点运动的路程和位移大小相等,均为1 m,选项D正确。
8.(多选)下列关于矢量(位移)和标量(温度)的说法中,正确的是
A.两运动物体的位移大小均为30 m,这两个位移不一定相同
B.做直线运动的两物体的位移x甲=3 m,x乙=-5 m,则x甲>x乙
C.温度计读数有正有负,其正负号表示温度方向
D.温度计读数的正负号表示温度的高低
√
√
两物体的位移大小虽然均为30 m,但由于不知其方向关系,两个位移不一定相同,A正确;比较物体位移大小应比较其绝对值,B错误;温度无方向,其正负表示温度的高低,C错误,D正确。
9.(2024·陕西安康高一校联考期末)如图所示,自行车的车轮半径为R,车轮沿直线无滑动地滚动,当气门芯由轮子的正上方第一次运动到轮子正下方时,气门芯位移的大小为
A.πR B.2R
C.2πR D. R
√
当气门芯由轮子的正上方第一次运动到轮子正下方时轮子向前运动半个周长,气门芯在水平方向上移动的距离为πR,在竖直方向上移动的距离为2R,由勾股定理可知,气门芯位移的大小为
R。
10.如图为A、B两人在同一直线上运动的位移—时间图像,下列分析正确的是
A.0~2 s内,A、B两人同向而行
B.0~2 s内,A单位时间内的位移比B的大
C.前5 s内,A的路程比B的路程小
D.前5 s内,A的位移比B的位移小
√
由位移—时间图像可以看出,0~2 s内,A沿负方向运动,B沿正方向运动,两人运动方向相反,故A错误;0~2 s内,A的位移为-24 m,单位时间(每秒)内的位移为-12 m;B的位移为60 m,单位时间(每秒)内的位移为30 m,正负
号表示方向,故B错误;前5 s内,B正向运动60 m,静止2 s后又负向运动30 m,即B的路程为90 m;A的路程为60 m,故A的路程比B的路程小,故C正确;前5 s内,A的位移大小为60 m,B的位移大小为30 m,故A的位移大于B的位移,故D错误。
11.(10分)某班级的教室在3楼,每天同学们都要从1楼爬到3楼上课。如图所示,若每层楼的高度都是3 m,楼梯的倾角为45°,某同学从楼梯沿折线从大门走到3楼教室门口,他走过的位移大小是多少?路程是多少?(把某同学爬楼过程等效为物体沿坡滑行)
答案:6 m 6 m
由题图可知,折线为某同学的运动轨迹,每个斜梯长为1.5 m,
路程l=4×1.5 m=6 m。
初位置在大门口,末位置在教室门口,从初位置到末位置的有向线段为位移,所以位移大小为x=2h=6 m。
12.(10分)如图所示,实心长方体木块ABCD-A′B′C′D′的长、宽、高分别为a、b、c,且a>b>c。有一个小虫自A′点运动到C点,求:
(1)小虫的位移大小;
答案:
小虫的位移大小为由A′指向C的有向线段的长度,为x=
(2)小虫的最小路程。
答案:
小虫的最小路程应等于将ABCD-A′B′C′D′展开后A′C之间的连线长度,
返回
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
