教科版高中物理必修第一册 第二章 匀变速直线运动的规律 3 匀变速直线运动位移与时间的关系 课件(共60张PPT)
文档属性
| 名称 | 教科版高中物理必修第一册 第二章 匀变速直线运动的规律 3 匀变速直线运动位移与时间的关系 课件(共60张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-28 19:48:43 | ||
图片预览









文档简介
(共60张PPT)
3.匀变速直线运动位移与时间的关系
第二章 匀变速直线运动的规律
1.知道匀变速直线运动的位移与v-t图线和时间轴所围面积的对应关系。
2.体会利用极限思想解决物理问题的科学思维方法。
3.了解位移公式的推导方法,会应用位移公式解决实际问题。
4.理解匀变速直线运动中间时刻的瞬时速度公式和平均速度公式,并会用其解决实际问题。
素养目标
知识点一 匀变速直线运动的位移
自主学习
情境导入 1.如图为匀速直线运动的v-t图像,图中阴影部分的面积与物体在0~t1时间内的位移在数值上是否相等?
提示:相等
2.做匀变速运动的物体,在时间t内的位移与时间的关系是否也可以用v-t图像中图线与时间轴所围的面积表示?
提示:可以
教材梳理 (阅读教材P42—P43完成下列填空)
1.极限思想的理解
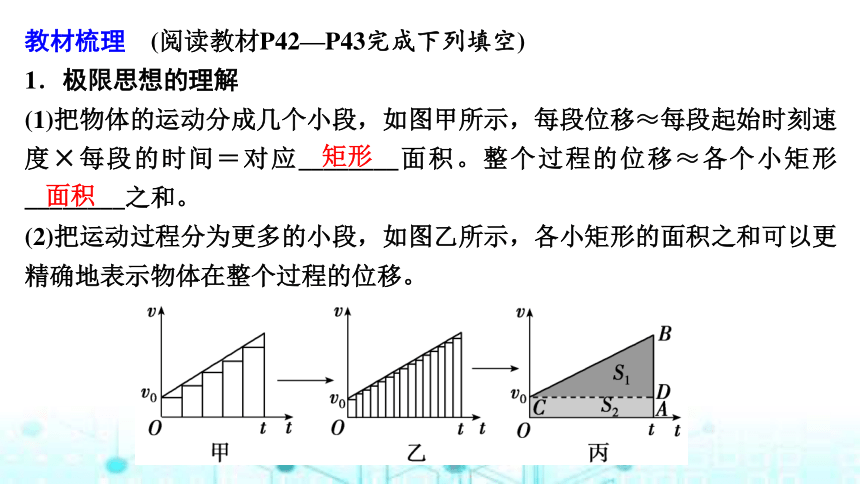
(1)把物体的运动分成几个小段,如图甲所示,每段位移≈每段起始时刻速度×每段的时间=对应________面积。整个过程的位移≈各个小矩形________之和。
(2)把运动过程分为更多的小段,如图乙所示,各小矩形的面积之和可以更精确地表示物体在整个过程的位移。
矩形
面积
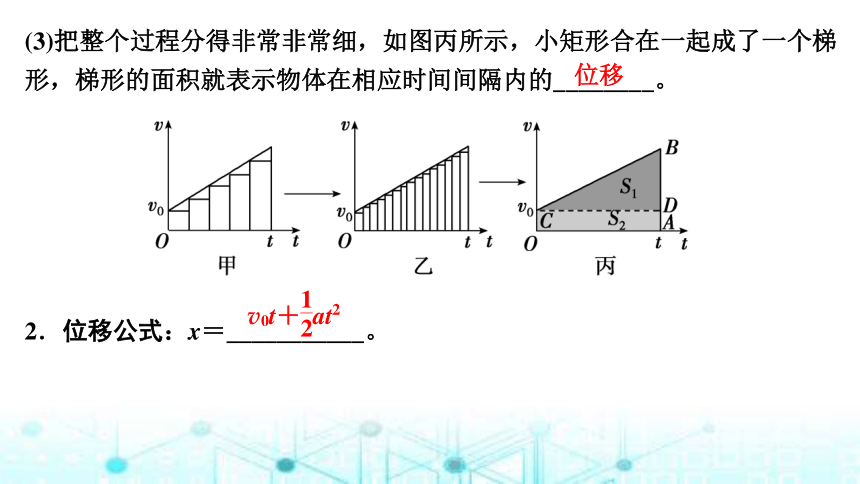
(3)把整个过程分得非常非常细,如图丙所示,小矩形合在一起成了一个梯形,梯形的面积就表示物体在相应时间间隔内的________。
2.位移公式:x=___________。
位移
课堂探究
师生互动 对于匀变速直线运动位移与时间的关系式x=v0t+ at2。
任务1.公式是否适用于匀减速直线运动?
提示:适用
任务2.公式中的矢量有哪些?解题时需注意什么?
提示:矢量有x、v0、a,需规定正方向
任务3.如果物体的初速度为零,写出公式的简化形式。
提示:x= at2
角度1 公式x=v0t+ at2的理解
一物体运动的位移与时间的关系为x=(6t+4t2) m,则
A.这个物体的初速度为8 m/s
B.这个物体的初速度为12 m/s
C.这个物体的加速度为-8 m/s2
D.这个物体的加速度为8 m/s2
例1
√
根据匀变速直线运动的位移公式x=v0t+ at2,结合位移—时间函数x=(6t+4t2)m,比较可得v0=6 m/s,a=8 m/s2,即物体沿正方向做匀加速直线运动,故D正确,A、B、C错误。
角度2 公式x=v0t+ at2的应用
一物体做匀加速直线运动,初速度为v0=5 m/s,加速度为a=2 m/s2,求:
(1)物体在前3 s内通过的位移大小;
答案:24 m
例2
前3 s内的位移大小
x=v0t+ at2=5×3 m+ ×2×32 m=24 m。
(2)物体在第3 s内通过的位移大小。
答案:10 m
前2 s内的位移大小
x′=v0t′+ at′2=5×2 m+ ×2×22 m=14 m
第3 s内的位移大小
x″=x-x′=(24-14) m=10 m。
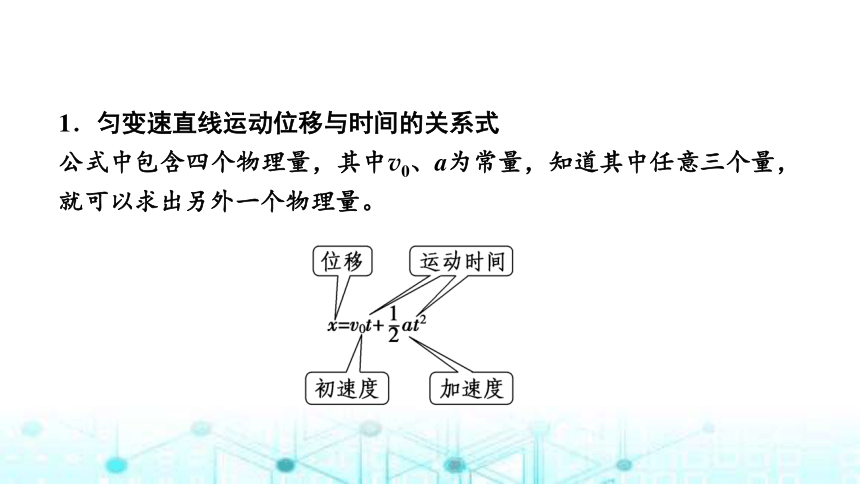
1.匀变速直线运动位移与时间的关系式
公式中包含四个物理量,其中v0、a为常量,知道其中任意三个量,就可以求出另外一个物理量。
2.矢量性:公式中x、v0、a都是矢量,应用时必须选取统一的正方向。
3.两种特殊形式
(1)当a=0时,x=v0t(匀速直线运动)。
(2)当v0=0时,x= at2(由静止开始的匀加速直线运动,x∝t2)。
通常选取初速度的方向为正方向 a、v0同向时,a取正值
a、v0反向时,a取负值
位移的计算结果 位移为正值说明位移方向与规定的正方向相同
位移为负值说明位移方向与规定的正方向相反
针对练1.(2024·湖南常德高一期中)如图所示,假设列车在某段铁轨做匀加速直线运动,速度由5 m/s 增加到10 m/s时位移为x1,则当速度由10 m/s增加到15 m/s时,它的位移是
√
解析:列车做匀加速直线运动,有5 m/s+at=10 m/s,10 m/s+at=15
m/s,x1=5 m/s·t+ at2,x2=10 m/s·t+ at2,联立解得x2= x1,故B正确。
C.2x1 D.3x1
针对练2.(多选)一个做匀变速直线运动的物体,某时刻的速度大小为4 m/s,1 s后速度的大小为10 m/s,在这1 s内该物体的
A.位移大小可能小于4 m
B.位移大小可能大于10 m
C.加速度的大小可能小于4 m/s2
D.加速度的大小可能大于10 m/s2
√
√
以初速度的方向为正方向,当二者同向时,a= m/s2=6 m/s2,x=v1t+ at2=7 m;当二者反向时,a= m/s2=-14 m/s2,x=v1t+ at2=-3 m,故选AD。
返回
知识点二 平均速度公式的应用
自主学习
1.平均速度公式:
匀变速直线运动中任意一段时间t内的平均速度等于该段时间的中间时刻的瞬时速度,还等于该段时间初、末速度矢量和的一半。
2.推导:设物体做匀变速直线运动的初速度为v0,加速度为a,t时刻的速度为vt
某汽车从车站由静止开出,做匀加速直线运动,运动了12 s时,发现还有乘客没上来,于是汽车立即做匀减速运动至停下,共历时20 s,运动了50 m,求汽车在上述运动中的最大速度。
答案:5 m/s
例3
解析:法一:基本公式法
设最大速度为vmax,
由题意得x=x1+x2= a1t12+vmaxt2- a2t22,
t=t1+t2,vmax=a1t1,0=vmax-a2t2,
解得vmax=5 m/s。
法二:平均速度法
由于汽车在前、后两阶段均做匀变速直线运动,故前、后两阶段的平均速度均为最大速度vmax的一半,
结合x= t,解得vmax= =5 m/s。
针对练1.如图为世界一级方程式锦标赛(简称F1)中某赛车直线加速的情景。假设赛车启动时从静止开始做匀加速直线运动,达到速度v所需时间为t,则此过程赛车的运动距离为
A.vt
B.
C.2vt
D.不能确定
√
赛车加速运动距离为x= ,故B正确。
针对练2.一物体做匀加速直线运动,通过一段位移Δx所用时间为t1。紧接着通过下一段位移Δx所用时间为t2,则该物体运动的加速度为
√
返回
知识点三 利用v-t图像求位移
角度1 v-t图像的定性分析
(2024·江苏宝应期中)2023年世界泳联跳水世界杯蒙特利尔站,全红婵获得女子10米跳台冠军,为国家争得了荣誉。如图甲所示为模拟她比赛时的示意图,图乙为其竖直方向的速度与时间的关系图像,以其离开跳台作为计时起点,则下列说法正确的是
A.t2时刻到达最高点
B.t1时刻开始进入水中
C.t2时刻开始进入水中
D.t3时刻开始进入水中
例4
√
自主学习
全红婵起跳时的速度方向向上,而t1时刻竖直速度为零,说明全红婵到达最高点,A、B错误;在0~t2时间内全红婵在空中运动,从t2时刻开始减速,所以t2时刻开始进入水中,t3时刻到达水中最深处,速度减为0,C正确,D错误。
针对练.(多选)(2024·福建漳州高一期中)如图是P、Q两质点,从同一地点由静止开始运动的v-t图像,由图线可以判定
A.P质点的速度越来越小
B.零时刻P质点的加速度为零
C.在0~t1时间内,P质点在Q质点前面
D.在0~t1时间内,P质点的平均速度大于Q质点的平均速度
√
√
从题图中可以看出在0~t1时间内,P质点的速度越来越大,A错误;在v-t图像中,切线斜率表示加速度,所以零时刻P质点的速度虽然为零,但是斜率(即加速度)不为零,B错误;在0~t1时间内,P质点的位移大
于Q质点的位移,因P、Q两质点从同一地点由静止开始运动,则P质点
在Q质点前面,根据 可知,在0~t1时间内,P质点的平均速度大于Q质点的平均速度,C、D正确。
角度2 v-t图像的定量计算
(多选)汽车以10 m/s的速度在平直公路上匀速行驶,驾驶员发现正前方的斑马线上有行人,于是刹车礼让,汽车恰好停在斑马线前。假设驾驶员的反应时间为0.5 s,汽车运动的v-t图像如图所示。下列说法中正确的是
例5
A.在驾驶员反应时间内,汽车行驶的距离为5 m
B.从驾驶员发现情况到汽车停止,共行驶的距离为15 m
C.汽车刹车时的加速度大小为10 m/s2
D.从驾驶员发现情况到汽车停止的平均速度为6 m/s
√
√
√
汽车在驾驶员的反应时间内做匀速直线运动,则反应时间内汽车行驶的距离x1=vt1=10×0.5 m=5 m,故A正确;根据v-t图像中图线与时间轴所包围的“面积”表示物体通过的位移可知,从驾驶员发现情况到汽车停止,共行驶的距离x=10×0.5 m
+ ×10×2 m=15 m,故B正确;匀减速运动的加速度大小a=
m/s2=5 m/s2,故C错误;从驾驶员发现情况到汽车停止的平均速度
m/s=6 m/s,故D正确。
利用v-t图像求位移
1.v-t图像与t轴所围的“面积”表示位移。
2.“面积”在t轴以上是正值,表示位移沿正方向;在t轴以下是负值,表示位移沿负方向。
3.物体的总位移等于各部分位移(正、负“面积”)的代数和。
4.物体通过的路程为t轴上、下“面积”绝对值的和。
针对练.(多选)某物体做直线运动的v-t图像如图所示,下列说法正确的是
A.物体在前2 s内的位移大小为4 m
B.物体在前3 s内通过的路程为5 m
C.物体在前3 s内的平均速度大小为 m/s
D.物体在前3 s内做非匀变速直线运动
√
√
返回
v-t图像中图线与时间轴所围成图形的面积表示位
移,则前2 s内的位移x1= ×4×2 m=4 m,A正确;物体在第3 s内位移大小x2= ×2×1 m=1
m,物体在前3 s内通过的路程为s=x1+x2=5 m,B正确;物体在前3 s内的位移x=x1-x2=3 m,则
前3 s内的平均速度为 m/s=1 m/s,C错误;v-t图像的斜率表示
物体的加速度,图像在前3 s内是一条倾斜直线,斜率不变,物体做匀变速直线运动,D错误。
随堂演练
1.(人教必修第一册P45拓展学习改编)图中甲、乙、丙是高中物理课本中推导匀变速直线运动的位移公式所用的v-t图像,下列说法正确的是
A.推导中把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法
B.图甲用矩形面积的和表示位移大小比图丙用梯形面积表示位移大小更接近真实值
C.这种用面积表示位移的方法只适用于匀变速直线运动
D.若图丙中纵坐标表示运动的加速度,则梯形面积表示加速度的变化量
√
根据v-t图像推导位移公式采用了微元法,A正确;v-t图像中图线与时间轴所围面积表示位移,可知题图丙用梯形面积表示位移比题图甲用矩形面积的和表示位移更接近真实值,B错误;用面积表示位移的方法适用于任何直线运动,C错误;若题图丙中纵坐标表示运动的加速度,则由Δv=aΔt知,梯形面积表示速度的变化量,D错误。
2.假设某型号飞机试飞时做匀加速直线运动,初速度大小为v0=30 m/s,加速度大小为a=5 m/s2,则飞机在3 s内的位移大小和第3 s内的位移大小分别为
A.112.5 m,42.5 m B.112.5 m,112.5 m
C.70 m,70 m D.70 m,112.5 m
√
飞机试飞时做匀加速直线运动,根据匀变速直线运动的位移与时间的关系式可得,飞机在3 s内的位移大小为x3=v0t3+ at32=30×3 m+ × 5×32 m=112.5 m,同理飞机在2 s内的位移大小为x2=v0t2+ at22=30×2 m+ ×5×22 m=70 m,因此第3 s内的位移大小为x=x3-x2=112.5 m-70 m=42.5 m,A正确。
3.(粤教必修第一册P56T2)按规定,卡车在市区行驶的速度不得超过40 km/h。一辆卡车在紧急情况下刹车,测得卡车滑行过程中车轮在路面上擦过的笔直的痕迹长9 m。从监控资料上知道,该车急刹后经过1.5 s停止。试判断该车是否超速。
答案:超速
将该车的运动看做匀减速运动,则根据x= ·t
可得v= m/s=12 m/s=43.2 km/h>40 km/h,则该车超速。
4.某一做直线运动的物体的v-t图像如图所示,根据图像求:
(1)物体距出发点的最远距离;
答案:6 m
v-t图像与时间轴所围的面积表示物体的位移,物体距出发点最远的距离为0~3 s内的位移,
则x1= ×4×3 m=6 m。
(2)前4 s内物体的位移;
答案:5 m
3~4 s内的位移x2=- ×2×1 m=-1 m,前4 s内物体的位移x=x1+x2=6 m-1 m=5 m。
(3)前4 s内物体通过的路程。
答案:7 m
前4 s内物体通过的路程等于前3 s内位移大小和后1 s内位移大小之和,则前4 s内物体通过的路程s=x1+|x2|=6 m+1 m=7 m。
返回
课 时 测 评
1.几个做匀变速直线运动的物体,在时间t内位移最大的是
A.加速度最大的物体 B.初速度最大的物体
C.末速度最大的物体 D.平均速度最大的物体
√
根据匀变速直线运动的位移公式x=v0t+ at2,当时间t一定时,位移x与a、v0都有关,A、B、C错误;根据平均速度定义式有x= t,当时
间t一定时, 越大,则x越大,D正确。
2.(2024·江西上饶期末)某质点从静止开始做匀加速直线运动,加速度大小为5 m/s2,则开始运动的前4 s内质点的位移大小是
A.20 m B.30 m
C.40 m D.50 m
√
根据匀变速直线运动的位移时间关系可知x= at2= ×5×42 m=40 m,选项C正确。
3.在交警处理某次交通事故时,通过监控仪器扫描,输入计算机后得到该汽车在水平面上刹车过程中的位移随时间变化的规律为x=20t-2t2(x的单位是m,t的单位是s)。则该汽车在路面上留下的刹车痕迹长度为
A.25 m B.50 m
C.100 m D.200 m
√
根据x=20t-2t2可知,该汽车初速度v0=20 m/s,加速度a=-4 m/s2,则刹车时间t= s=5 s,刹车后做匀减速运动的位移为刹车痕迹长度,根据x=v0t+ at2得x=20×5 m- ×4×52 m=50 m,B正确。
4.(人教必修第一册P46T3改编)速度、加速度的测量通常比位移的测量要复杂些,而有时我们只需比较两个物体运动的加速度大小,并不需要知道加速度的具体数值。例如比较两辆汽车的加速性能就是这样。若已知两辆汽车由静止开始做匀加速直线运动,在相同时间内两车的位移之比为2∶1,则它们的加速度之比为
A.1∶2 B.1∶4
C.2∶1 D.4∶1
√
根据x= at2可得a= ,由于时间相等,位移之比为2∶1,则加速度之比为2∶1,C正确。
5.(多选)(2024·浙江宁波期末)一个物体以v0=8 m/s的初速度沿光滑斜面向上滑,加速度的大小为2 m/s2,冲上最高点之后,又以相同的加速度往回运动。则
A.1 s末的速度大小为6 m/s
B.3 s末的速度为零
C.2 s内的位移大小是12 m
D.5 s内的位移大小是15 m
√
√
√
6.一物体从斜面上某点由静止开始做匀加速直线运动,经过3 s后到达斜面底端,并在水平地面上做匀减速直线运动,又经9 s停止,则物体在斜面上的位移与在水平地面上的位移大小之比是
A.1∶1 B.1∶2
C.1∶3 D.3∶1
√
7.一物体沿直线运动,其速度v随时间t变化关系的图像如图所示。由图像可知
A.0~2.0 s内的加速度小于2.0~3.0 s内的加速度
B.0~2.0 s内的位移小于2.0~3.0 s内的位移
C.0~2.0 s内的平均速度小于2.0~3.0 s内的平均速度
D.0~3.0 s内物体的运动方向发生了改变
√
根据v-t图像的斜率表示加速度,斜率的绝对值越大,加速度越大,则可知0~2.0 s内的加速度小于2.0~3.0 s内的加速度,A正确;根据v-t图像与时间轴围成的面积表示位移,则可知0~2.0 s内的位移大于2.0~3.0
s内的位移,B错误;根据匀变速直线运动的平均速度公式 ,可知0~2.0 s内与2.0~3.0 s内的平均速度相等,均为1.0 m/s,C错误;速
度的正负表示物体的运动方向,由题图知,0~3.0 s内物体的速度一直为正,运动方向不变,D错误。
8.(多选)(2024·广东汕头高一期中)一质点做匀加速直线运动,第3 s内的位移是2 m,第4 s内的位移是2.5 m,下列说法正确的是
A.第2 s内的位移是1.0 m
B.第2 s末的瞬时速度是1.75 m/s
C.前3 s的平均速度是2 m/s
D.质点的加速度是0.5 m/s2
√
√
因做匀变速直线运动的物体相邻相等时间内的位移之差相等,可知x4-x3=x3-x2,则第2 s内的位移是x2=1.5 m,A错误; 第2 s末的瞬时速度
等于1~3 s内的平均速度,即v2= m/s=1.75 m/s,B正确;前3 s的平均速度等于1.5 s时的瞬时速度,也等于第2 s内的平均速度,即 m/s=1.5 m/s,C错误;质点的加速度a=
m/s2=0.5 m/s2,D正确。故选BD。
9.(多选)假如一艘快艇在海面上运动的v-t图像如图所示。则下列说法中正确的是
A.快艇在0~66 s内从静止出发做加速度增大的加速直线运动
B.快艇在96 s末开始调头
C.快艇在66 s末离初始位置最远
D.快艇在96~116 s内沿负方向做匀加速直线运动
√
√
根据v-t图像某点处切线的斜率表示该点处的加速度,再结合题图可知,0~66 s内快艇做加速度逐渐减小的加速直线运动,故选项A错误;66 s末快艇开始减速,96 s末减速到零,此时离初始位置最远,然后开始调头,故选项B正确,C错误;在96~116 s内,速度为负,加速度为负且为定值,说明快艇沿负方向做匀加速直线运动,故选项D正确。
10.(多选)小明将一个质量很大、体积很小的小球从空中静止释放,小球与水平地面相碰后弹到空中某一高度,其v-t图像如图所示,下列判断正确的是
A.小球能弹起的最大高度为5 m
B.小球能弹起的最大高度为1.8 m
C.小球下落的最大速度为6 m/s
D.小球与地面碰撞过程中速度变化量-16 m/s
√
√
小球能弹起的最大高度等于v-t图像在1.0~
1.6 s时间内的“面积”大小,即有h= ×
0.6×6 m=1.8 m,A错误,B正确;由v-t
图像可知,t=1.0 s时刻小球下落的速度最大,为10 m/s,C错误;小球与地面碰撞前、
后速度分别为10 m/s、-6 m/s,所以小球与地面碰撞过程中速度变化量为Δv=-6 m/s-10 m/s=-16 m/s,D正确。
11.(10分)骑自行车的人以5 m/s的初速度匀减速地上一个斜坡(如图所示),加速度的大小为0.4 m/s2,斜坡长30 m,骑自行车的人通过斜坡需要多少时间?
答案:10 s
把x=30 m、v0=5 m/s和a=-0.4 m/s2代入位移公式x=v0t+ at2
解得t1=10 s,t2=15 s
将t1=10 s和t2=15 s分别代入速度公式vt=v0+at计算两个对应的末速度,v1=1 m/s和v2=-1 m/s(与上坡的速度方向相反,与实际情况不符,所以应该舍去)
故人通过斜坡需要10 s的时间。
12.(10分)一辆汽车以72 km/h的速度正在平直公路上匀速行驶,突然发现前方40 m处有需要紧急停车的危险信号,司机立即采取刹车措施。已知该车在刹车过程中加速度的大小为5 m/s2,则从刹车开始经过5 s时汽车前进的距离是多少?此时是否已经到达危险区域?
答案:40 m 否
设汽车由刹车开始至停止运动所用的时间为t0,选初速度方向为正方向,由于汽车做匀减速直线运动,加速度a=-5 m/s2,v0=72 km/h=20
m/s,则由vt=v0+at0,得t0= s=4 s
可见,该汽车刹车后经过4 s就已停下,其后的时间内汽车是静止的,由位移公式x=v0t+ at2知,刹车后经过 5 s汽车通过的距离为x=v0t0+ at02= m=40 m
即汽车在此时恰好未到达危险区域。
返回
3.匀变速直线运动位移与时间的关系
第二章 匀变速直线运动的规律
1.知道匀变速直线运动的位移与v-t图线和时间轴所围面积的对应关系。
2.体会利用极限思想解决物理问题的科学思维方法。
3.了解位移公式的推导方法,会应用位移公式解决实际问题。
4.理解匀变速直线运动中间时刻的瞬时速度公式和平均速度公式,并会用其解决实际问题。
素养目标
知识点一 匀变速直线运动的位移
自主学习
情境导入 1.如图为匀速直线运动的v-t图像,图中阴影部分的面积与物体在0~t1时间内的位移在数值上是否相等?
提示:相等
2.做匀变速运动的物体,在时间t内的位移与时间的关系是否也可以用v-t图像中图线与时间轴所围的面积表示?
提示:可以
教材梳理 (阅读教材P42—P43完成下列填空)
1.极限思想的理解
(1)把物体的运动分成几个小段,如图甲所示,每段位移≈每段起始时刻速度×每段的时间=对应________面积。整个过程的位移≈各个小矩形________之和。
(2)把运动过程分为更多的小段,如图乙所示,各小矩形的面积之和可以更精确地表示物体在整个过程的位移。
矩形
面积
(3)把整个过程分得非常非常细,如图丙所示,小矩形合在一起成了一个梯形,梯形的面积就表示物体在相应时间间隔内的________。
2.位移公式:x=___________。
位移
课堂探究
师生互动 对于匀变速直线运动位移与时间的关系式x=v0t+ at2。
任务1.公式是否适用于匀减速直线运动?
提示:适用
任务2.公式中的矢量有哪些?解题时需注意什么?
提示:矢量有x、v0、a,需规定正方向
任务3.如果物体的初速度为零,写出公式的简化形式。
提示:x= at2
角度1 公式x=v0t+ at2的理解
一物体运动的位移与时间的关系为x=(6t+4t2) m,则
A.这个物体的初速度为8 m/s
B.这个物体的初速度为12 m/s
C.这个物体的加速度为-8 m/s2
D.这个物体的加速度为8 m/s2
例1
√
根据匀变速直线运动的位移公式x=v0t+ at2,结合位移—时间函数x=(6t+4t2)m,比较可得v0=6 m/s,a=8 m/s2,即物体沿正方向做匀加速直线运动,故D正确,A、B、C错误。
角度2 公式x=v0t+ at2的应用
一物体做匀加速直线运动,初速度为v0=5 m/s,加速度为a=2 m/s2,求:
(1)物体在前3 s内通过的位移大小;
答案:24 m
例2
前3 s内的位移大小
x=v0t+ at2=5×3 m+ ×2×32 m=24 m。
(2)物体在第3 s内通过的位移大小。
答案:10 m
前2 s内的位移大小
x′=v0t′+ at′2=5×2 m+ ×2×22 m=14 m
第3 s内的位移大小
x″=x-x′=(24-14) m=10 m。
1.匀变速直线运动位移与时间的关系式
公式中包含四个物理量,其中v0、a为常量,知道其中任意三个量,就可以求出另外一个物理量。
2.矢量性:公式中x、v0、a都是矢量,应用时必须选取统一的正方向。
3.两种特殊形式
(1)当a=0时,x=v0t(匀速直线运动)。
(2)当v0=0时,x= at2(由静止开始的匀加速直线运动,x∝t2)。
通常选取初速度的方向为正方向 a、v0同向时,a取正值
a、v0反向时,a取负值
位移的计算结果 位移为正值说明位移方向与规定的正方向相同
位移为负值说明位移方向与规定的正方向相反
针对练1.(2024·湖南常德高一期中)如图所示,假设列车在某段铁轨做匀加速直线运动,速度由5 m/s 增加到10 m/s时位移为x1,则当速度由10 m/s增加到15 m/s时,它的位移是
√
解析:列车做匀加速直线运动,有5 m/s+at=10 m/s,10 m/s+at=15
m/s,x1=5 m/s·t+ at2,x2=10 m/s·t+ at2,联立解得x2= x1,故B正确。
C.2x1 D.3x1
针对练2.(多选)一个做匀变速直线运动的物体,某时刻的速度大小为4 m/s,1 s后速度的大小为10 m/s,在这1 s内该物体的
A.位移大小可能小于4 m
B.位移大小可能大于10 m
C.加速度的大小可能小于4 m/s2
D.加速度的大小可能大于10 m/s2
√
√
以初速度的方向为正方向,当二者同向时,a= m/s2=6 m/s2,x=v1t+ at2=7 m;当二者反向时,a= m/s2=-14 m/s2,x=v1t+ at2=-3 m,故选AD。
返回
知识点二 平均速度公式的应用
自主学习
1.平均速度公式:
匀变速直线运动中任意一段时间t内的平均速度等于该段时间的中间时刻的瞬时速度,还等于该段时间初、末速度矢量和的一半。
2.推导:设物体做匀变速直线运动的初速度为v0,加速度为a,t时刻的速度为vt
某汽车从车站由静止开出,做匀加速直线运动,运动了12 s时,发现还有乘客没上来,于是汽车立即做匀减速运动至停下,共历时20 s,运动了50 m,求汽车在上述运动中的最大速度。
答案:5 m/s
例3
解析:法一:基本公式法
设最大速度为vmax,
由题意得x=x1+x2= a1t12+vmaxt2- a2t22,
t=t1+t2,vmax=a1t1,0=vmax-a2t2,
解得vmax=5 m/s。
法二:平均速度法
由于汽车在前、后两阶段均做匀变速直线运动,故前、后两阶段的平均速度均为最大速度vmax的一半,
结合x= t,解得vmax= =5 m/s。
针对练1.如图为世界一级方程式锦标赛(简称F1)中某赛车直线加速的情景。假设赛车启动时从静止开始做匀加速直线运动,达到速度v所需时间为t,则此过程赛车的运动距离为
A.vt
B.
C.2vt
D.不能确定
√
赛车加速运动距离为x= ,故B正确。
针对练2.一物体做匀加速直线运动,通过一段位移Δx所用时间为t1。紧接着通过下一段位移Δx所用时间为t2,则该物体运动的加速度为
√
返回
知识点三 利用v-t图像求位移
角度1 v-t图像的定性分析
(2024·江苏宝应期中)2023年世界泳联跳水世界杯蒙特利尔站,全红婵获得女子10米跳台冠军,为国家争得了荣誉。如图甲所示为模拟她比赛时的示意图,图乙为其竖直方向的速度与时间的关系图像,以其离开跳台作为计时起点,则下列说法正确的是
A.t2时刻到达最高点
B.t1时刻开始进入水中
C.t2时刻开始进入水中
D.t3时刻开始进入水中
例4
√
自主学习
全红婵起跳时的速度方向向上,而t1时刻竖直速度为零,说明全红婵到达最高点,A、B错误;在0~t2时间内全红婵在空中运动,从t2时刻开始减速,所以t2时刻开始进入水中,t3时刻到达水中最深处,速度减为0,C正确,D错误。
针对练.(多选)(2024·福建漳州高一期中)如图是P、Q两质点,从同一地点由静止开始运动的v-t图像,由图线可以判定
A.P质点的速度越来越小
B.零时刻P质点的加速度为零
C.在0~t1时间内,P质点在Q质点前面
D.在0~t1时间内,P质点的平均速度大于Q质点的平均速度
√
√
从题图中可以看出在0~t1时间内,P质点的速度越来越大,A错误;在v-t图像中,切线斜率表示加速度,所以零时刻P质点的速度虽然为零,但是斜率(即加速度)不为零,B错误;在0~t1时间内,P质点的位移大
于Q质点的位移,因P、Q两质点从同一地点由静止开始运动,则P质点
在Q质点前面,根据 可知,在0~t1时间内,P质点的平均速度大于Q质点的平均速度,C、D正确。
角度2 v-t图像的定量计算
(多选)汽车以10 m/s的速度在平直公路上匀速行驶,驾驶员发现正前方的斑马线上有行人,于是刹车礼让,汽车恰好停在斑马线前。假设驾驶员的反应时间为0.5 s,汽车运动的v-t图像如图所示。下列说法中正确的是
例5
A.在驾驶员反应时间内,汽车行驶的距离为5 m
B.从驾驶员发现情况到汽车停止,共行驶的距离为15 m
C.汽车刹车时的加速度大小为10 m/s2
D.从驾驶员发现情况到汽车停止的平均速度为6 m/s
√
√
√
汽车在驾驶员的反应时间内做匀速直线运动,则反应时间内汽车行驶的距离x1=vt1=10×0.5 m=5 m,故A正确;根据v-t图像中图线与时间轴所包围的“面积”表示物体通过的位移可知,从驾驶员发现情况到汽车停止,共行驶的距离x=10×0.5 m
+ ×10×2 m=15 m,故B正确;匀减速运动的加速度大小a=
m/s2=5 m/s2,故C错误;从驾驶员发现情况到汽车停止的平均速度
m/s=6 m/s,故D正确。
利用v-t图像求位移
1.v-t图像与t轴所围的“面积”表示位移。
2.“面积”在t轴以上是正值,表示位移沿正方向;在t轴以下是负值,表示位移沿负方向。
3.物体的总位移等于各部分位移(正、负“面积”)的代数和。
4.物体通过的路程为t轴上、下“面积”绝对值的和。
针对练.(多选)某物体做直线运动的v-t图像如图所示,下列说法正确的是
A.物体在前2 s内的位移大小为4 m
B.物体在前3 s内通过的路程为5 m
C.物体在前3 s内的平均速度大小为 m/s
D.物体在前3 s内做非匀变速直线运动
√
√
返回
v-t图像中图线与时间轴所围成图形的面积表示位
移,则前2 s内的位移x1= ×4×2 m=4 m,A正确;物体在第3 s内位移大小x2= ×2×1 m=1
m,物体在前3 s内通过的路程为s=x1+x2=5 m,B正确;物体在前3 s内的位移x=x1-x2=3 m,则
前3 s内的平均速度为 m/s=1 m/s,C错误;v-t图像的斜率表示
物体的加速度,图像在前3 s内是一条倾斜直线,斜率不变,物体做匀变速直线运动,D错误。
随堂演练
1.(人教必修第一册P45拓展学习改编)图中甲、乙、丙是高中物理课本中推导匀变速直线运动的位移公式所用的v-t图像,下列说法正确的是
A.推导中把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法
B.图甲用矩形面积的和表示位移大小比图丙用梯形面积表示位移大小更接近真实值
C.这种用面积表示位移的方法只适用于匀变速直线运动
D.若图丙中纵坐标表示运动的加速度,则梯形面积表示加速度的变化量
√
根据v-t图像推导位移公式采用了微元法,A正确;v-t图像中图线与时间轴所围面积表示位移,可知题图丙用梯形面积表示位移比题图甲用矩形面积的和表示位移更接近真实值,B错误;用面积表示位移的方法适用于任何直线运动,C错误;若题图丙中纵坐标表示运动的加速度,则由Δv=aΔt知,梯形面积表示速度的变化量,D错误。
2.假设某型号飞机试飞时做匀加速直线运动,初速度大小为v0=30 m/s,加速度大小为a=5 m/s2,则飞机在3 s内的位移大小和第3 s内的位移大小分别为
A.112.5 m,42.5 m B.112.5 m,112.5 m
C.70 m,70 m D.70 m,112.5 m
√
飞机试飞时做匀加速直线运动,根据匀变速直线运动的位移与时间的关系式可得,飞机在3 s内的位移大小为x3=v0t3+ at32=30×3 m+ × 5×32 m=112.5 m,同理飞机在2 s内的位移大小为x2=v0t2+ at22=30×2 m+ ×5×22 m=70 m,因此第3 s内的位移大小为x=x3-x2=112.5 m-70 m=42.5 m,A正确。
3.(粤教必修第一册P56T2)按规定,卡车在市区行驶的速度不得超过40 km/h。一辆卡车在紧急情况下刹车,测得卡车滑行过程中车轮在路面上擦过的笔直的痕迹长9 m。从监控资料上知道,该车急刹后经过1.5 s停止。试判断该车是否超速。
答案:超速
将该车的运动看做匀减速运动,则根据x= ·t
可得v= m/s=12 m/s=43.2 km/h>40 km/h,则该车超速。
4.某一做直线运动的物体的v-t图像如图所示,根据图像求:
(1)物体距出发点的最远距离;
答案:6 m
v-t图像与时间轴所围的面积表示物体的位移,物体距出发点最远的距离为0~3 s内的位移,
则x1= ×4×3 m=6 m。
(2)前4 s内物体的位移;
答案:5 m
3~4 s内的位移x2=- ×2×1 m=-1 m,前4 s内物体的位移x=x1+x2=6 m-1 m=5 m。
(3)前4 s内物体通过的路程。
答案:7 m
前4 s内物体通过的路程等于前3 s内位移大小和后1 s内位移大小之和,则前4 s内物体通过的路程s=x1+|x2|=6 m+1 m=7 m。
返回
课 时 测 评
1.几个做匀变速直线运动的物体,在时间t内位移最大的是
A.加速度最大的物体 B.初速度最大的物体
C.末速度最大的物体 D.平均速度最大的物体
√
根据匀变速直线运动的位移公式x=v0t+ at2,当时间t一定时,位移x与a、v0都有关,A、B、C错误;根据平均速度定义式有x= t,当时
间t一定时, 越大,则x越大,D正确。
2.(2024·江西上饶期末)某质点从静止开始做匀加速直线运动,加速度大小为5 m/s2,则开始运动的前4 s内质点的位移大小是
A.20 m B.30 m
C.40 m D.50 m
√
根据匀变速直线运动的位移时间关系可知x= at2= ×5×42 m=40 m,选项C正确。
3.在交警处理某次交通事故时,通过监控仪器扫描,输入计算机后得到该汽车在水平面上刹车过程中的位移随时间变化的规律为x=20t-2t2(x的单位是m,t的单位是s)。则该汽车在路面上留下的刹车痕迹长度为
A.25 m B.50 m
C.100 m D.200 m
√
根据x=20t-2t2可知,该汽车初速度v0=20 m/s,加速度a=-4 m/s2,则刹车时间t= s=5 s,刹车后做匀减速运动的位移为刹车痕迹长度,根据x=v0t+ at2得x=20×5 m- ×4×52 m=50 m,B正确。
4.(人教必修第一册P46T3改编)速度、加速度的测量通常比位移的测量要复杂些,而有时我们只需比较两个物体运动的加速度大小,并不需要知道加速度的具体数值。例如比较两辆汽车的加速性能就是这样。若已知两辆汽车由静止开始做匀加速直线运动,在相同时间内两车的位移之比为2∶1,则它们的加速度之比为
A.1∶2 B.1∶4
C.2∶1 D.4∶1
√
根据x= at2可得a= ,由于时间相等,位移之比为2∶1,则加速度之比为2∶1,C正确。
5.(多选)(2024·浙江宁波期末)一个物体以v0=8 m/s的初速度沿光滑斜面向上滑,加速度的大小为2 m/s2,冲上最高点之后,又以相同的加速度往回运动。则
A.1 s末的速度大小为6 m/s
B.3 s末的速度为零
C.2 s内的位移大小是12 m
D.5 s内的位移大小是15 m
√
√
√
6.一物体从斜面上某点由静止开始做匀加速直线运动,经过3 s后到达斜面底端,并在水平地面上做匀减速直线运动,又经9 s停止,则物体在斜面上的位移与在水平地面上的位移大小之比是
A.1∶1 B.1∶2
C.1∶3 D.3∶1
√
7.一物体沿直线运动,其速度v随时间t变化关系的图像如图所示。由图像可知
A.0~2.0 s内的加速度小于2.0~3.0 s内的加速度
B.0~2.0 s内的位移小于2.0~3.0 s内的位移
C.0~2.0 s内的平均速度小于2.0~3.0 s内的平均速度
D.0~3.0 s内物体的运动方向发生了改变
√
根据v-t图像的斜率表示加速度,斜率的绝对值越大,加速度越大,则可知0~2.0 s内的加速度小于2.0~3.0 s内的加速度,A正确;根据v-t图像与时间轴围成的面积表示位移,则可知0~2.0 s内的位移大于2.0~3.0
s内的位移,B错误;根据匀变速直线运动的平均速度公式 ,可知0~2.0 s内与2.0~3.0 s内的平均速度相等,均为1.0 m/s,C错误;速
度的正负表示物体的运动方向,由题图知,0~3.0 s内物体的速度一直为正,运动方向不变,D错误。
8.(多选)(2024·广东汕头高一期中)一质点做匀加速直线运动,第3 s内的位移是2 m,第4 s内的位移是2.5 m,下列说法正确的是
A.第2 s内的位移是1.0 m
B.第2 s末的瞬时速度是1.75 m/s
C.前3 s的平均速度是2 m/s
D.质点的加速度是0.5 m/s2
√
√
因做匀变速直线运动的物体相邻相等时间内的位移之差相等,可知x4-x3=x3-x2,则第2 s内的位移是x2=1.5 m,A错误; 第2 s末的瞬时速度
等于1~3 s内的平均速度,即v2= m/s=1.75 m/s,B正确;前3 s的平均速度等于1.5 s时的瞬时速度,也等于第2 s内的平均速度,即 m/s=1.5 m/s,C错误;质点的加速度a=
m/s2=0.5 m/s2,D正确。故选BD。
9.(多选)假如一艘快艇在海面上运动的v-t图像如图所示。则下列说法中正确的是
A.快艇在0~66 s内从静止出发做加速度增大的加速直线运动
B.快艇在96 s末开始调头
C.快艇在66 s末离初始位置最远
D.快艇在96~116 s内沿负方向做匀加速直线运动
√
√
根据v-t图像某点处切线的斜率表示该点处的加速度,再结合题图可知,0~66 s内快艇做加速度逐渐减小的加速直线运动,故选项A错误;66 s末快艇开始减速,96 s末减速到零,此时离初始位置最远,然后开始调头,故选项B正确,C错误;在96~116 s内,速度为负,加速度为负且为定值,说明快艇沿负方向做匀加速直线运动,故选项D正确。
10.(多选)小明将一个质量很大、体积很小的小球从空中静止释放,小球与水平地面相碰后弹到空中某一高度,其v-t图像如图所示,下列判断正确的是
A.小球能弹起的最大高度为5 m
B.小球能弹起的最大高度为1.8 m
C.小球下落的最大速度为6 m/s
D.小球与地面碰撞过程中速度变化量-16 m/s
√
√
小球能弹起的最大高度等于v-t图像在1.0~
1.6 s时间内的“面积”大小,即有h= ×
0.6×6 m=1.8 m,A错误,B正确;由v-t
图像可知,t=1.0 s时刻小球下落的速度最大,为10 m/s,C错误;小球与地面碰撞前、
后速度分别为10 m/s、-6 m/s,所以小球与地面碰撞过程中速度变化量为Δv=-6 m/s-10 m/s=-16 m/s,D正确。
11.(10分)骑自行车的人以5 m/s的初速度匀减速地上一个斜坡(如图所示),加速度的大小为0.4 m/s2,斜坡长30 m,骑自行车的人通过斜坡需要多少时间?
答案:10 s
把x=30 m、v0=5 m/s和a=-0.4 m/s2代入位移公式x=v0t+ at2
解得t1=10 s,t2=15 s
将t1=10 s和t2=15 s分别代入速度公式vt=v0+at计算两个对应的末速度,v1=1 m/s和v2=-1 m/s(与上坡的速度方向相反,与实际情况不符,所以应该舍去)
故人通过斜坡需要10 s的时间。
12.(10分)一辆汽车以72 km/h的速度正在平直公路上匀速行驶,突然发现前方40 m处有需要紧急停车的危险信号,司机立即采取刹车措施。已知该车在刹车过程中加速度的大小为5 m/s2,则从刹车开始经过5 s时汽车前进的距离是多少?此时是否已经到达危险区域?
答案:40 m 否
设汽车由刹车开始至停止运动所用的时间为t0,选初速度方向为正方向,由于汽车做匀减速直线运动,加速度a=-5 m/s2,v0=72 km/h=20
m/s,则由vt=v0+at0,得t0= s=4 s
可见,该汽车刹车后经过4 s就已停下,其后的时间内汽车是静止的,由位移公式x=v0t+ at2知,刹车后经过 5 s汽车通过的距离为x=v0t0+ at02= m=40 m
即汽车在此时恰好未到达危险区域。
返回
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
