初中数学人教版九年级上册 24.1.2 垂直于弦的直径 教学设计
文档属性
| 名称 | 初中数学人教版九年级上册 24.1.2 垂直于弦的直径 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 49.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-28 15:43:42 | ||
图片预览


文档简介
《24.1.2垂直于弦的直径》
一、教材分析
圆有许多重要性质,其中最主要性质是圆的对称性,在探索、发现和证明圆的许多重要性质时,都运用了它的对称性。同时圆的对称性在日常生活和生产中有着广泛的应用,因此这一节的内容在整章中具有举足轻重的意义。“圆的对称性”第一课时的主要内容是垂径定理及其逆定理,它反映了圆的重要性质,是圆的轴对称性的具体化,也是证明线段相等、角相等、弧相等、垂直关系的重要依据,同时也为圆的计算和作图提供了方法与依据。所以本节知识的学习与方法的积累直接影响着后续有关圆知识的学习。
二、教学设计
(一)环节一:
1.学习目标:通过折叠,感知圆的轴对称,能找出圆的对称轴,掌握数学事实“圆是轴对称图形,任何一条直径所在的直线都是它的对称轴”,积累利用折叠研究几何图形的方法.
2.教学活动:利用圆的轴对称找圆形纸片或圆形实物的“圆心”。
问题1:有什么办法找出圆形纸片的圆心呢?动手试一试.
(动手操作,利用折叠方法折出两条折痕AB、CD,交点O就是圆心)
问题2:怎么验证点O就是圆心呢?
(方法:在圆上找一些点,测量它们与点O的距离,如果距离相等,那么根据到定点的距离等于定长的所有点组成的图形是圆,定点就是圆心。)
问题3:需要找几个点?一个?两个?三个?还是更多?
(交流:两点只能说明点O在线段的垂直平分线上,所以,至少要找三个点.)
问题4:你有办法找出圆形硬币的圆心吗?圆形花坛呢
3.评价任务:
知识评价:评价学生对圆的轴对称理解.
素养评价:评价几何的直观想象素养.
测评:圆是轴对称图形吗 对称轴几条?用圆形纸片折一折.
(圆是轴对称图形,对称轴有无数条,是任意一条过圆心的直线)
(二)环节二:
1.学习目标:经历观察、实验、猜想、论证的过程,探究垂径定理,了解垂径定理及推论,能用运动变化的观点体会从特殊到一般的研究问题方法,领会数学推理的严谨性.
2.教学活动:利用圆的轴对称性探究垂径定理,三种语言表示.垂径定理。
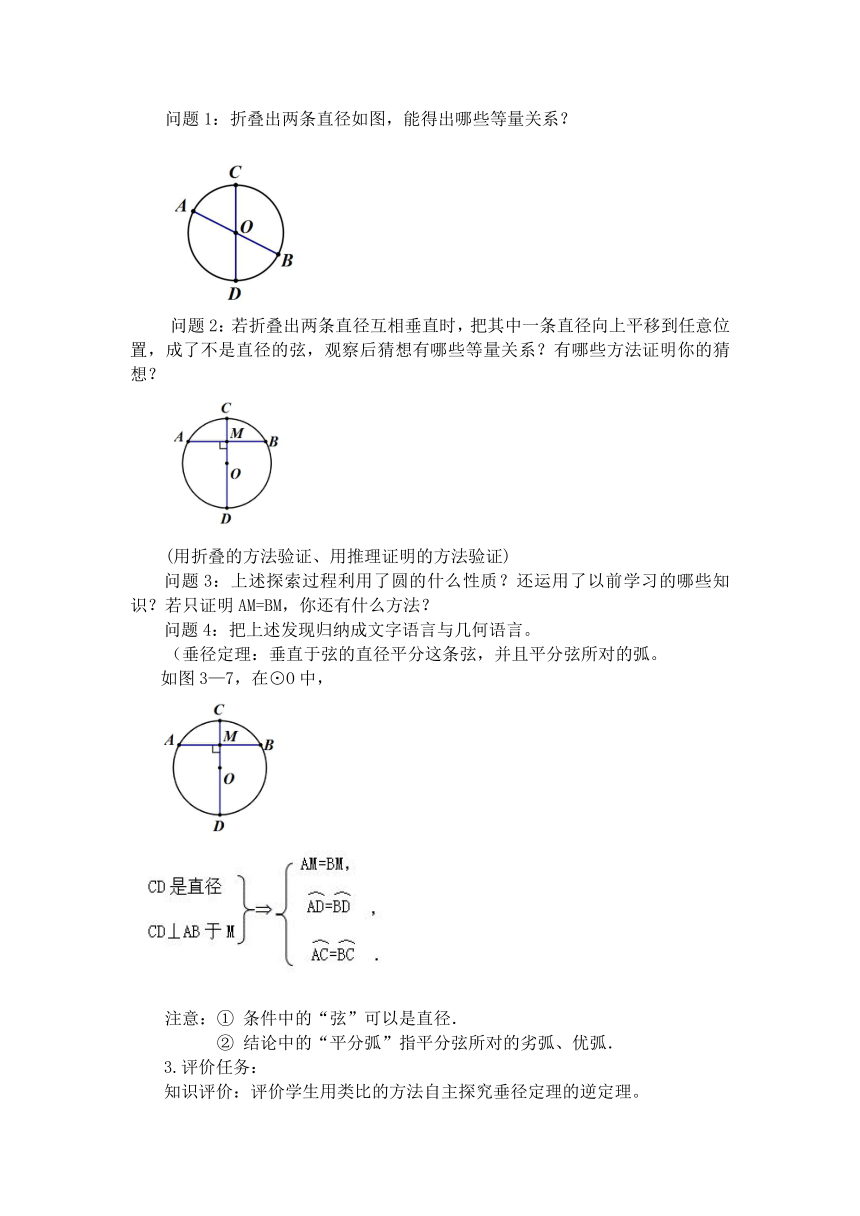
问题1:折叠出两条直径如图,能得出哪些等量关系?
问题2:若折叠出两条直径互相垂直时,把其中一条直径向上平移到任意位置,成了不是直径的弦,观察后猜想有哪些等量关系?有哪些方法证明你的猜想?
(用折叠的方法验证、用推理证明的方法验证)
问题3:上述探索过程利用了圆的什么性质?还运用了以前学习的哪些知识?若只证明AM=BM,你还有什么方法?
问题4:把上述发现归纳成文字语言与几何语言。
(垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
如图3—7,在⊙O中,
注意:① 条件中的“弦”可以是直径.
② 结论中的“平分弧”指平分弦所对的劣弧、优弧.
3.评价任务:
知识评价:评价学生用类比的方法自主探究垂径定理的逆定理。
素养评价:体会类比与归纳的数学思想,评价逻辑推理素养。
测评1.把垂径定理中条件“垂直于弦”与结论“平分于弦”互换,结论是否还成立?写成命题的形式,并判断是真命题还是假命题?
测评2. 把上述发现归纳成文字语言. 并思考为何条件强调“弦不是直径”?还能写出垂径定理的其它逆命题吗?判断是真命题还是假命题?并进行归类。
(垂径定理逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。由条件“直径、垂直于弦、平分弦、平分优弧、平分劣弧”任已知两个可以得出另三个,如弦的垂直平分线必是直径所在的直线等.)
(三)环节三:
1.学习目标:通过作图与计算,应用垂径定理及推论解决“平分弧”和“找圆心”等问题,能从垂径定理中提取基本图形通过构建方程解决相关问题,养成数学应用意识,体会数学与生活的联系。
2.教学活动:运用垂径定理及其逆定理进行有关的计算和证明。
问题1:现在你有办法找出圆形花坛的圆心吗?
问题2:已知:如图⊙O中,直径CD⊥AB,垂足为点M,
①若半径R=5,OM=3,求AB、CM的长;
②若半径R=5,AB=8,求OM、CM的长;
③由①②两题的启发,你还能编出其它什么问题?
④从中你能找出什么规律?
3.评价任务:
知识评价:学生运用新知进行的计算和证明。
素养评价:评价数学建模与数学运算素养。
测评1.如右图所示,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上一点,且OE⊥CD,垂足为F,EF=90 m.求这段弯路的半径.
测评2.如图,⊙O中,弦AB∥CD,直径EF⊥AB于点M,交CD于点N,则有
哪些相等的线段,有哪些相等的劣弧, 为什么?
测评3.这节课在内容方面你学习了哪些知识?在方法方面你学会了什么?你还有什么疑惑吗?有什么体会与感悟与我们交流?
三、对“教—学—评”三位一体的教学思考
(一)将课堂教学目标进行分解是落实有效“教”的前提
1.教学目标既是教与学的出发点,也是教与学的归宿点。清晰的目标是“教-学-评一致性”的前提和灵魂。清晰的教学目标是教学的关键,是处理教材和选择教法的依据,也是评价课堂教学效果的标准。没有清晰的目标,就无所谓教-学-评的活动;没有清晰的目标,也就无所谓一致性,因为判断教-学-评是否一致的依据就是教学、学习与评价是否都是围绕共享的目标展开。
2.学习目标是课标中教学目标的科学细化有效分解。课标中所给出的目标是学段学习目标,它属于上位目标,和实际课堂教学之间还有一定的距离。因此,从目标达成的视角来看,这些目标是不易评价的,也难于检验课堂的有效程度。因此,教师需认真研读课程标准的内涵,结合学情和教学内容将其分解、细化为可操作、有针对性的课时学习目标。学习目标的主体不是教师而是学生,学习目标的行为动词不是“培养、指导”,而是“了解、掌握、能、会经历、感悟”等动词,主体不同,行为动词就不同了。如本节课标的教学目标是“探索并证明垂径定理”,教参中教学目标是“探索并证明垂径定理,发展推理能力”,这样的教学目标是笼统的、不具体,不可测又不可评,无法体现能力与素养。在教学评一致性的理念下,把这个教学目标细化分解成可测可评的学习目标有六条:①通过折叠,能找出圆的对称轴;②掌握数学事实“圆是轴对称图形,任何一条直径所在的直线都是它的对称轴”;③经历观察、实验、猜想、论证的过程,探究垂径定理;④了解垂径定理及推论;⑤通过作图与计算,应用垂径定理及推论解决“平分弧”和“找圆心”等问题;⑥能从垂径定理中提取基本图形通过构建方程解决相关问题。细化后的六条可测可评的目标分别在三个不同的教学活动环节中实现,每个活动环节分别有两个细化后的学习目标。学习目标与评价任务的对应关系不一定是一一对应,每个环节都有一个完整的“教、学、评”,相对独立又相互联系,前后连贯、逻辑一致。
(二)围绕目标进行教学活动设计是落实有效“学”的保证
1.教学活动是安排和组织评价任务,催生学习信息,达成学习目标的过程
数学教育家斯托利亚尔指出:“积极地数学教学,应为数学活动(思维活动)的教学,而不是数学活动结果——数学知识的教学”。有效教学的根本是学生对所学知识的体验程度,教学设计就要对课堂教学内容进行优化重组,要围绕目标进行有针对性地设计教学活动。这样的课堂才有针对性,才能让学生少走弯路,体验知识的生产过程,感受数学知识的来龙去脉,体验思维的过程。每个环节的教学活动都应围绕细化分解后的一到两条的学习目标展开。
2.教学活动的落实关键看学生“学”的情况
教师不应该把数学当作一个已经完成了的形式理论来教,不应该将各种定义、规则、算法灌输给学生,而是应该创造合适的条件,让学生在学习数学的过程中用自己的体验、自己的思维方式,重新创造数学知识。基于此,教师通过设计恰当的学生活动,为学生搭建逻辑连贯的思维平台,把数学的学术形态转化为学生易于接受的教育形态,在冰冷的美丽与火热的思考之间寻找平衡点。
(三)围绕目标进行评价任务设计是落实有效“评”的关键
华师大崔永漷教授认为“没有评价的教学如同逛街”。评价任务设计要有指向性、可执行与空间感。评价任务的指向性是评价任务要指向学习目标,即评价任务与学习目标一致性;评价任务的可执行是指评价任务要清晰具体,让学生可说、可做、可写、可表达,不全是“你真棒,你很棒!”;评价任务的空间感是指评价任务的设计要有多样性与开放性。目前,大部分的数学课堂教学目标和课堂实施之间存在一定的距离,脱节现象时有存在,更重要的是缺少评价目标达成情况的标准. 教学的有效性就是对目标达成情况进行分析,制订目标达成程度的评价标准,切实落实目标达成.只有更多地关注可测性或量化,教学才会更有效。通过每一个教学环节,能看出学生到底有没有得到进步和发展,发展程度如何,能及时评价课堂教学的达成度和课堂教学中学生学习的效果。
教学评价不是指一个相对完整的教学阶段终结时实施的活动,不是孤立与教学活动之外教或学之后再来评的独立环节,也不是一个人教和另一个人学了之后等待第三者来评的那个孤立的环节,而是教学环节的一个重要组成部分,不断地检测学生的学习进程,不断地对学生的学习进行评价,同时决定调整教学进程。评价不仅仅是知识掌握的评价,更要关注核心素养的评价。教学、学习、评价是三位一体的关系,评价与教学、学习紧密地绞缠在一起,相互制约,相互影响。
一、教材分析
圆有许多重要性质,其中最主要性质是圆的对称性,在探索、发现和证明圆的许多重要性质时,都运用了它的对称性。同时圆的对称性在日常生活和生产中有着广泛的应用,因此这一节的内容在整章中具有举足轻重的意义。“圆的对称性”第一课时的主要内容是垂径定理及其逆定理,它反映了圆的重要性质,是圆的轴对称性的具体化,也是证明线段相等、角相等、弧相等、垂直关系的重要依据,同时也为圆的计算和作图提供了方法与依据。所以本节知识的学习与方法的积累直接影响着后续有关圆知识的学习。
二、教学设计
(一)环节一:
1.学习目标:通过折叠,感知圆的轴对称,能找出圆的对称轴,掌握数学事实“圆是轴对称图形,任何一条直径所在的直线都是它的对称轴”,积累利用折叠研究几何图形的方法.
2.教学活动:利用圆的轴对称找圆形纸片或圆形实物的“圆心”。
问题1:有什么办法找出圆形纸片的圆心呢?动手试一试.
(动手操作,利用折叠方法折出两条折痕AB、CD,交点O就是圆心)
问题2:怎么验证点O就是圆心呢?
(方法:在圆上找一些点,测量它们与点O的距离,如果距离相等,那么根据到定点的距离等于定长的所有点组成的图形是圆,定点就是圆心。)
问题3:需要找几个点?一个?两个?三个?还是更多?
(交流:两点只能说明点O在线段的垂直平分线上,所以,至少要找三个点.)
问题4:你有办法找出圆形硬币的圆心吗?圆形花坛呢
3.评价任务:
知识评价:评价学生对圆的轴对称理解.
素养评价:评价几何的直观想象素养.
测评:圆是轴对称图形吗 对称轴几条?用圆形纸片折一折.
(圆是轴对称图形,对称轴有无数条,是任意一条过圆心的直线)
(二)环节二:
1.学习目标:经历观察、实验、猜想、论证的过程,探究垂径定理,了解垂径定理及推论,能用运动变化的观点体会从特殊到一般的研究问题方法,领会数学推理的严谨性.
2.教学活动:利用圆的轴对称性探究垂径定理,三种语言表示.垂径定理。
问题1:折叠出两条直径如图,能得出哪些等量关系?
问题2:若折叠出两条直径互相垂直时,把其中一条直径向上平移到任意位置,成了不是直径的弦,观察后猜想有哪些等量关系?有哪些方法证明你的猜想?
(用折叠的方法验证、用推理证明的方法验证)
问题3:上述探索过程利用了圆的什么性质?还运用了以前学习的哪些知识?若只证明AM=BM,你还有什么方法?
问题4:把上述发现归纳成文字语言与几何语言。
(垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
如图3—7,在⊙O中,
注意:① 条件中的“弦”可以是直径.
② 结论中的“平分弧”指平分弦所对的劣弧、优弧.
3.评价任务:
知识评价:评价学生用类比的方法自主探究垂径定理的逆定理。
素养评价:体会类比与归纳的数学思想,评价逻辑推理素养。
测评1.把垂径定理中条件“垂直于弦”与结论“平分于弦”互换,结论是否还成立?写成命题的形式,并判断是真命题还是假命题?
测评2. 把上述发现归纳成文字语言. 并思考为何条件强调“弦不是直径”?还能写出垂径定理的其它逆命题吗?判断是真命题还是假命题?并进行归类。
(垂径定理逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。由条件“直径、垂直于弦、平分弦、平分优弧、平分劣弧”任已知两个可以得出另三个,如弦的垂直平分线必是直径所在的直线等.)
(三)环节三:
1.学习目标:通过作图与计算,应用垂径定理及推论解决“平分弧”和“找圆心”等问题,能从垂径定理中提取基本图形通过构建方程解决相关问题,养成数学应用意识,体会数学与生活的联系。
2.教学活动:运用垂径定理及其逆定理进行有关的计算和证明。
问题1:现在你有办法找出圆形花坛的圆心吗?
问题2:已知:如图⊙O中,直径CD⊥AB,垂足为点M,
①若半径R=5,OM=3,求AB、CM的长;
②若半径R=5,AB=8,求OM、CM的长;
③由①②两题的启发,你还能编出其它什么问题?
④从中你能找出什么规律?
3.评价任务:
知识评价:学生运用新知进行的计算和证明。
素养评价:评价数学建模与数学运算素养。
测评1.如右图所示,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上一点,且OE⊥CD,垂足为F,EF=90 m.求这段弯路的半径.
测评2.如图,⊙O中,弦AB∥CD,直径EF⊥AB于点M,交CD于点N,则有
哪些相等的线段,有哪些相等的劣弧, 为什么?
测评3.这节课在内容方面你学习了哪些知识?在方法方面你学会了什么?你还有什么疑惑吗?有什么体会与感悟与我们交流?
三、对“教—学—评”三位一体的教学思考
(一)将课堂教学目标进行分解是落实有效“教”的前提
1.教学目标既是教与学的出发点,也是教与学的归宿点。清晰的目标是“教-学-评一致性”的前提和灵魂。清晰的教学目标是教学的关键,是处理教材和选择教法的依据,也是评价课堂教学效果的标准。没有清晰的目标,就无所谓教-学-评的活动;没有清晰的目标,也就无所谓一致性,因为判断教-学-评是否一致的依据就是教学、学习与评价是否都是围绕共享的目标展开。
2.学习目标是课标中教学目标的科学细化有效分解。课标中所给出的目标是学段学习目标,它属于上位目标,和实际课堂教学之间还有一定的距离。因此,从目标达成的视角来看,这些目标是不易评价的,也难于检验课堂的有效程度。因此,教师需认真研读课程标准的内涵,结合学情和教学内容将其分解、细化为可操作、有针对性的课时学习目标。学习目标的主体不是教师而是学生,学习目标的行为动词不是“培养、指导”,而是“了解、掌握、能、会经历、感悟”等动词,主体不同,行为动词就不同了。如本节课标的教学目标是“探索并证明垂径定理”,教参中教学目标是“探索并证明垂径定理,发展推理能力”,这样的教学目标是笼统的、不具体,不可测又不可评,无法体现能力与素养。在教学评一致性的理念下,把这个教学目标细化分解成可测可评的学习目标有六条:①通过折叠,能找出圆的对称轴;②掌握数学事实“圆是轴对称图形,任何一条直径所在的直线都是它的对称轴”;③经历观察、实验、猜想、论证的过程,探究垂径定理;④了解垂径定理及推论;⑤通过作图与计算,应用垂径定理及推论解决“平分弧”和“找圆心”等问题;⑥能从垂径定理中提取基本图形通过构建方程解决相关问题。细化后的六条可测可评的目标分别在三个不同的教学活动环节中实现,每个活动环节分别有两个细化后的学习目标。学习目标与评价任务的对应关系不一定是一一对应,每个环节都有一个完整的“教、学、评”,相对独立又相互联系,前后连贯、逻辑一致。
(二)围绕目标进行教学活动设计是落实有效“学”的保证
1.教学活动是安排和组织评价任务,催生学习信息,达成学习目标的过程
数学教育家斯托利亚尔指出:“积极地数学教学,应为数学活动(思维活动)的教学,而不是数学活动结果——数学知识的教学”。有效教学的根本是学生对所学知识的体验程度,教学设计就要对课堂教学内容进行优化重组,要围绕目标进行有针对性地设计教学活动。这样的课堂才有针对性,才能让学生少走弯路,体验知识的生产过程,感受数学知识的来龙去脉,体验思维的过程。每个环节的教学活动都应围绕细化分解后的一到两条的学习目标展开。
2.教学活动的落实关键看学生“学”的情况
教师不应该把数学当作一个已经完成了的形式理论来教,不应该将各种定义、规则、算法灌输给学生,而是应该创造合适的条件,让学生在学习数学的过程中用自己的体验、自己的思维方式,重新创造数学知识。基于此,教师通过设计恰当的学生活动,为学生搭建逻辑连贯的思维平台,把数学的学术形态转化为学生易于接受的教育形态,在冰冷的美丽与火热的思考之间寻找平衡点。
(三)围绕目标进行评价任务设计是落实有效“评”的关键
华师大崔永漷教授认为“没有评价的教学如同逛街”。评价任务设计要有指向性、可执行与空间感。评价任务的指向性是评价任务要指向学习目标,即评价任务与学习目标一致性;评价任务的可执行是指评价任务要清晰具体,让学生可说、可做、可写、可表达,不全是“你真棒,你很棒!”;评价任务的空间感是指评价任务的设计要有多样性与开放性。目前,大部分的数学课堂教学目标和课堂实施之间存在一定的距离,脱节现象时有存在,更重要的是缺少评价目标达成情况的标准. 教学的有效性就是对目标达成情况进行分析,制订目标达成程度的评价标准,切实落实目标达成.只有更多地关注可测性或量化,教学才会更有效。通过每一个教学环节,能看出学生到底有没有得到进步和发展,发展程度如何,能及时评价课堂教学的达成度和课堂教学中学生学习的效果。
教学评价不是指一个相对完整的教学阶段终结时实施的活动,不是孤立与教学活动之外教或学之后再来评的独立环节,也不是一个人教和另一个人学了之后等待第三者来评的那个孤立的环节,而是教学环节的一个重要组成部分,不断地检测学生的学习进程,不断地对学生的学习进行评价,同时决定调整教学进程。评价不仅仅是知识掌握的评价,更要关注核心素养的评价。教学、学习、评价是三位一体的关系,评价与教学、学习紧密地绞缠在一起,相互制约,相互影响。
同课章节目录
