教科版高中物理必修第一册 第三章 相互作用4 第1课时 力的合成 课件(共56张PPT)
文档属性
| 名称 | 教科版高中物理必修第一册 第三章 相互作用4 第1课时 力的合成 课件(共56张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-28 19:54:20 | ||
图片预览









文档简介
(共56张PPT)
4.力的合成
第三章 相互作用
第1课时 力的合成
1.知道合力、分力、力的合成等概念,能从力的作用效果上理解合力和分力。
2.理解共点力,体会力的合成是一种等效替代法。
3.理解平行四边形定则和三角形定则,会用作图法和计算法求合力和分力。
4.知道合力随分力夹角的变化情况,知道合力的取值范围。
素养目标
知识点一 几个力可以用一个力来替代
自主学习
情境导入 如图所示,一个成年人或两个孩子均能提起同一桶水,那么该成年人用的力与两个孩子用的力的作用效果是否相同?
提示:相同
教材梳理 (阅读教材P82完成下列填空)
1.合力、分力:如果力F的作用效果与力F1和F2共同作用的效果______,我们就称F为F1和F2的______,F1和F2为F的______。
2.力的合成:求几个力的______的过程。力的合成是一种__________的方法。
3.共点力:是指作用于物体上________,或者作用在同一物体上且力的________相交于同一点的几个力。
相同
合力
分力
合力
等效替代
同一点
作用线
课堂探究
师生互动 在上述情境导学中:
任务1.成年人用的力与两个孩子用的力是否同时作用在水桶上?
提示:不是
任务2.此时两个孩子用的力可不可以当作成年人用的力的两个分力?
提示:可以
任务3.合力与分力一定是同性质的力吗?
提示:不一定
(多选)关于两个分力F1、F2及它们的合力F,下列说法正确的是
A.合力F一定与F1、F2共同作用产生的效果相同
B.两力F1、F2一定是同种性质的力
C.两力F1、F2一定是同一个物体受的力
D.两力F1、F2与合力F可以是物体同时受到的三个力
例1
√
合力是对两个分力的等效替代,效果相同,故A正确;两个分力可以是同种性质的力,也可以是不同性质的力,故B错误;只有同一个物体受到的力才能合成,分别作用在不同物体上的力不能合成,故C正确;合力与分力不能同时存在,故D错误。
√
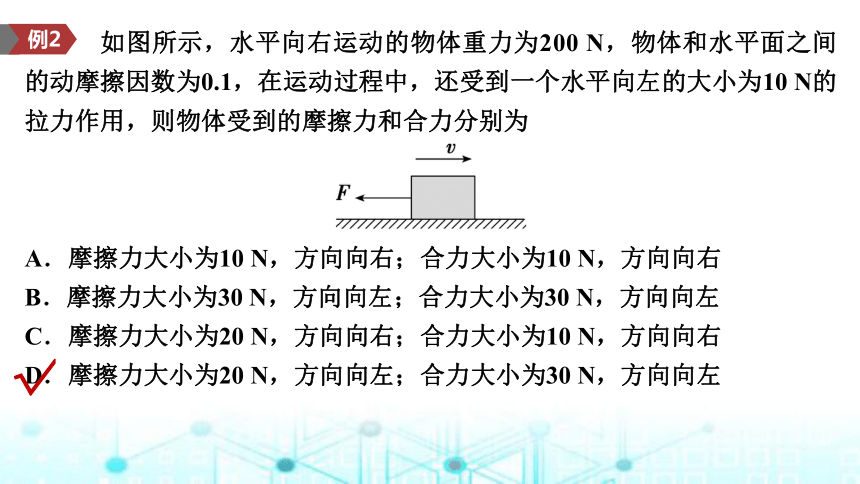
如图所示,水平向右运动的物体重力为200 N,物体和水平面之间的动摩擦因数为0.1,在运动过程中,还受到一个水平向左的大小为10 N的拉力作用,则物体受到的摩擦力和合力分别为
A.摩擦力大小为10 N,方向向右;合力大小为10 N,方向向右
B.摩擦力大小为30 N,方向向左;合力大小为30 N,方向向左
C.摩擦力大小为20 N,方向向右;合力大小为10 N,方向向右
D.摩擦力大小为20 N,方向向左;合力大小为30 N,方向向左
例2
√
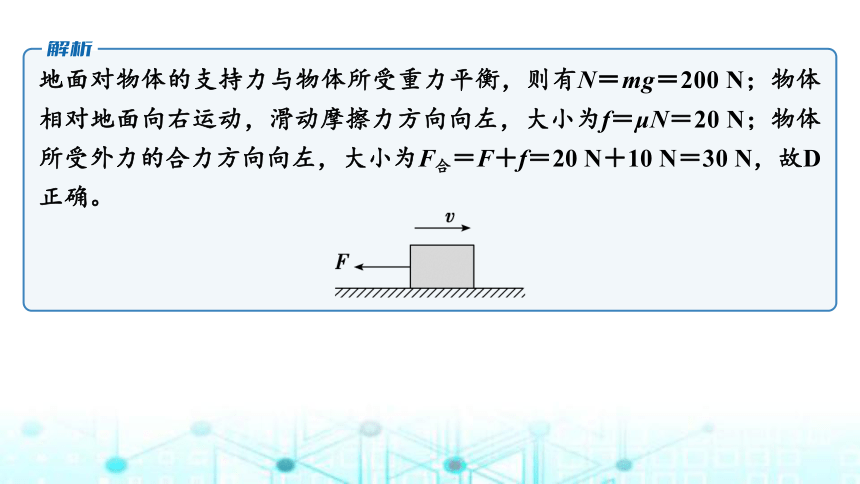
地面对物体的支持力与物体所受重力平衡,则有N=mg=200 N;物体相对地面向右运动,滑动摩擦力方向向左,大小为f=μN=20 N;物体所受外力的合力方向向左,大小为F合=F+f=20 N+10 N=30 N,故D正确。
1.合力与分力的关系:等效替代。可以是同性质的力,也可以是不同性质的力。
2.合力与分力的大小关系
(1)两分力同向(夹角θ=0°)时,合力最大,F=F1+F2,合力与分力同向。
(2)两分力反向(夹角θ=180°)时,合力最小,F=|F1-F2|,合力的方向与较大的一个分力的方向相同。
(3)合力的取值范围:|F1-F2|≤F≤F1+F2。
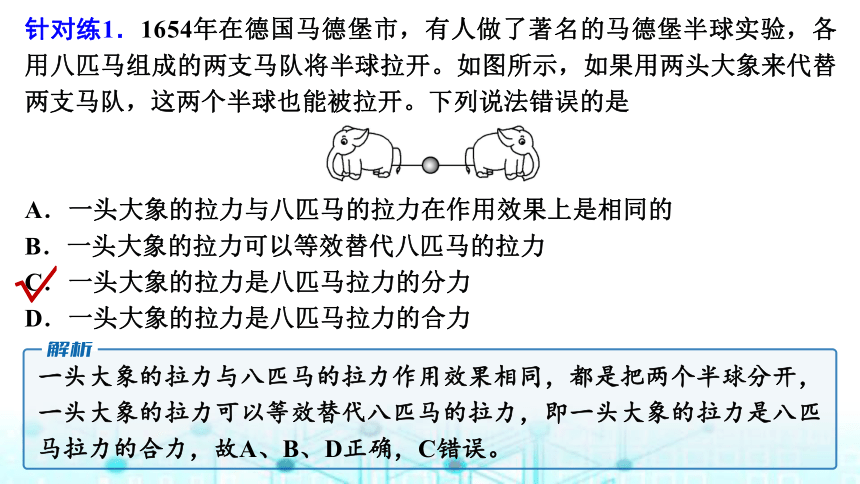
针对练1.1654年在德国马德堡市,有人做了著名的马德堡半球实验,各用八匹马组成的两支马队将半球拉开。如图所示,如果用两头大象来代替两支马队,这两个半球也能被拉开。下列说法错误的是
A.一头大象的拉力与八匹马的拉力在作用效果上是相同的
B.一头大象的拉力可以等效替代八匹马的拉力
C.一头大象的拉力是八匹马拉力的分力
D.一头大象的拉力是八匹马拉力的合力
√
一头大象的拉力与八匹马的拉力作用效果相同,都是把两个半球分开,一头大象的拉力可以等效替代八匹马的拉力,即一头大象的拉力是八匹马拉力的合力,故A、B、D正确,C错误。
针对练2.两个共点力的大小分别为F1=10 N,F2=12 N,它们的合力大小不可能等于
A.23 N B.2 N
C.9 N D.22 N
√
当两个力方向相反时,它们的合力最小,则有Fmin=F2-F1=2 N;当两个力方向相同时,它们的合力最大,则有Fmax=F2+F1=22 N,则它们的合力大小范围为2 N≤F≤22 N。故选A。
返回
知识点二 平行四边形定则
自主学习
情境导入 在知识点一情境导入中,成年人用的力F是否与两个孩子用的力F1、F2的大小之和相等?
提示:不相等
教材梳理 (阅读教材P84—P85完成下列填空)
1.平行四边形定则:如果用表示两个共点力F1和F2的线段为邻边作平行四边形,那么合力F的大小和方向就可以用这两个邻边之间的________表示出来。
2.三角形定则:平行四边形的一半是三角形,在求合力的时候,也可以把表示的原来两个力的有向线段首尾相接,然后再从第一个力的始端向第二个力的末端画一条__________,这个__________就可以表示原来两个力的合力。
对角线
有向线段
有向线段
课堂探究
师生互动 自制一个平行四边形模型(如图),结合模型讨论以下问题:
任务1.合力的大小和方向怎样随两个分力夹角的改变而改变?
提示:在两个分力的大小不变的情况下,两分力的夹角越小,合力的大小就越大;两分力的夹角越大,合力的大小越小。
任务2.合力是否总是大于两个分力?合力何时达到最大值?何时达到最小值?
提示:在两个分力的夹角为钝角时,合力的大小可能比分力小;当两个分力的夹角为0°时,合力最大;两个分力的夹角为180°时,合力最小。
师生互动 自制一个平行四边形模型(如图),结合模型讨论以下问题:
任务3.当两个分力之间的夹角分别为0°和180°时,它们的合力如何计算?
提示:当两分力的夹角为0°时,F合=F1+F2;当两个分力的夹角为180°时,F合=|F1-F2|。可见,当两个分力间夹角变化时,合力F合的大小和方向也会随之变化。
角度1 求两个力的合力
上海市的杨浦大桥是我国自行设计建造的双塔双索面叠合梁斜拉桥,如图甲所示。挺拔高耸的208 m主塔似一把利剑直刺苍穹,塔的两侧32对钢索连接主梁,呈扇面展开,如巨型琴弦,正弹奏着巨龙腾飞的奏鸣曲。假设斜拉桥中某对钢索与竖直方向的夹角都是30°,如图乙所示,每根钢索中的拉力都是3×104 N,那么它们对塔柱形成的合力有多大?方向如何?
答案:5.2×104 N 竖直向下
例3
由对称性可知,合力方向一定沿塔柱竖直向下,用两种方法计算合力的大小。
法一:作图法
如图1所示,自O点引两根有向线段OA和OB,
它们跟竖直方向的夹角都为30°,
取单位长度为1×104 N,
则OA和OB的长度都是3个单位长度,
量得对角线OC长约为5.2个单位长度,
所以合力的大小为F=5.2×1×104 N=5.2×104 N,方向竖直向下。
法二:计算法
如图2所示,根据这个平行四边形是一个菱形的特点,连
接AB,交OC于D,则AB与OC互相垂直平分
对于直角三角形AOD,∠AOD=30°,
则有F=2F1cos 30°=2×3×104× N≈5.2×104 N,方
向竖直向下。
角度2 求多个力的合力
(多选)三个共点力,大小分别为4 N、5 N、8 N,夹角任意,它们的合力大小可能是
A.18 N B.8 N
C.1 N D.0
例4
√
√
√
当三力的方向相同时,合力最大,最大为Fmax=4 N+5 N+8 N=17 N。前两个力的合力范围5 N-4 N≤F≤4 N+5 N,即1 N≤F≤9 N,当F=8 N时与第三个力等大反向时,合力为0。即合力的范围0≤F≤17 N,故选BCD。
如图所示,5个力同时作用于一点,5个力大小和方向相当于正六边形的两条边和三条对角线,已知F1 =10 N,则这5个力的合力的大小为
A.30 N
B.40 N
C.50 N
D.60 N
例5
√
解题指导:利用正六边形的几何特性,先将F1与F4合成,再将F2与F5合成,最后求5个力的合力。
如图所示,F1与F4合成时形成以F1和F4为邻作平行四边形,F3为所夹的对角线,即F1与F4的合力为F3,同理可知,F2与F5的合力也为F3,故5个力的合力等于3倍的F3,由几何关系可知F3的大小等于2倍的F1的大小,则5个力的合力大小为6F1=60 N,D正确。
1.作图法
(1)基本思路:
(2)如图所示:用作图法求F1、F2的合力F。
2.计算法
(1)两分力共线时:
①若F1、F2两力同向,则合力F=F1+F2,方向与两力同向。
②若F1、F2两力反向,则合力F=|F1-F2|,方向与两分力中较大者同向。
(2)两分力不共线时:根据平行四边形定则结合几何知识求合力。
常见求合力的三种特殊情况:
3.三个力的合力范围的确定方法
(1)最大值:三个力方向相同时,合力最大,Fmax=F1+F2+F3。
(2)最小值
①若三个力中任何一个力在另外两个力的合力大小范围内,则合力F的最小值为0,即Fmin=0;
②若三个力中任何一个力都不在另外两个力的合力大小范围内,设三个力中最大的一个力的大小为F3,则当大小为F1与F2的两个力方向相同且与大小为F3的力方向相反时,合力最小,Fmin=F3-(F1+F2)。
针对练1.如图所示,大小分别为F1、F2、F3的三个力恰好围成封闭的直角三角形(顶角为直角)。选项图中三个力的合力最大的是
√
由三角形定则可知,题图A中的合力的大小为2F1,题图B中的合力的大小为0,题图C中的合力的大小为2F2,题图D中的合力的大小为2F3,由于F2是直角三角形的斜边,所以F2最大,故合力最大的是C。
针对练2.如图所示,两个人共同用力将一个牌匾拉上墙头。其中一人用了450 N的拉力,另一人用了600 N的拉力,如果这两个人所用拉力的夹角是90°,求它们的合力。
答案:750 N,与较小拉力的夹角为53°
解析:法一:作图法
选择某一标度表示150 N的力。用一个点O代表牌匾,依题意作出两个拉力的图示,再作出力的平行四边形,如图所示。用刻度尺量出平行四边形的对角线长为图示线段的5倍,故合力大小为F=150×5 N= 750 N,用量角器量出合力F与F1的夹角θ= 53°。
法二:计算法
设F1=450 N,F2 =600 N,合力为F
由于F1与F2间的夹角为90°,根据勾股定理得
F= N=750 N,
合力F与F1的夹角θ的正切值 ,所以θ=53°。
返回
随堂演练
1.(人教必修第一册P75T5改编)下列关于合力和分力的说法中,正确的是
A.合力总比任何一个分力都大
B.两个力的合力至少比其中的一个分力大
C.合力的方向只与两分力的夹角有关
D.合力的大小介于两个分力之差的绝对值与两个分力之和之间
√
根据平行四边形定则可知,合力可能比分力大,可能比分力小,也可能与分力相等,A、B错误;根据平行四边形定则可知,合力的方向取决于两分力的大小和方向,C错误;合力的大小取值范围为|F1-F2|≤F≤ F1+F2,即合力的大小介于两个分力之差的绝对值与两个分力之和之间,D正确。
2.两个共点力的大小分别为3 N和4 N,它们的合力不可能是
A.2 N B.4 N
C.6 N D.8 N
√
两力合成时,合力范围为|F1-F2|≤F≤F1+F2,即1 N≤F≤7 N,则合力不可能是8 N。
3.(粤教必修第一册P81T3改编)有两个大小相等的共点力F1和F2。当它们间的夹角为90°时合力为F,则当它们间的夹角为120°时,合力的大小为
A.2F B. F
C. F D. F
√
4.两个人共同拉一头牛,每人的拉力大小和方向如图所示。请用图示法求出牛所受拉力的合力大小。
答案:180 N
由题图可知,F1、F2的图示所选标度为40 N,以
代表F1、F2的有向线段为邻边作平行四边形,F1、
F2所夹的对角线就表示了合力的大小和方向,如
图所示:
用刻度尺量得表示合力的线段长为4.5个标度,合
力为F= ×40 N=180 N。
返回
课 时 测 评
1.(多选)某同学通过以下步骤测出了从一定高度落下的排球对地面的冲击力:将一张白纸铺在水平地面上,把排球在水里弄湿,然后让排球从规定的高度自由落下,并在白纸上留下球的水印。再将印有水印的白纸铺在台秤上。将球放在纸上的水印中心,缓慢地向下压球,使排球与纸接触部分逐渐发生形变直至刚好遮住水印,记下此时台秤的示数即为冲击力的最大值。下列物理学习或研究中用到的方法与该同学的方法相近的是
A.通过平面镜观察桌面的微小形变
B.建立“合力与分力”的概念
C.建立“重心”的概念
D.建立“瞬时速度”的概念
√
√
由题可知,该同学用到了等效替代法。显示微小形变的过程利用了微小放大法,故A错误;建立“合力与分力”的概念用到了等效替代法,故B正确;建立“重心”的概念用到了等效替代法,故C正确;建立“瞬时速度”的概念用到了极限法,故D错误。
2.(多选)关于合力与其两个分力的关系,下列说法正确的是
A.合力的大小可能等于它的某一分力的大小
B.当两个分力的夹角θ逐渐增加时,其合力逐渐变大
C.有两个分力大小分别为7 N和10 N,其合力大小可能为5 N
D.合力一定至少大于其中一个分力
√
当两个分力的夹角θ逐渐增加时,其合力逐渐变小,故B错误;有两个分力大小分别为7 N 和10 N,其合力范围为3~17 N,故C正确;合力与分力遵循平行四边形定则,合力可以大于、等于或小于分力,故A正确,D错误。
√
3.如图所示,一个大人能提起一桶水并保持水桶静止,两个小孩也能共同提起一桶水并保持水桶静止,下列说法正确的是
A.小孩对水桶施加的两个力与这两个力的合力同时作用在水桶上
B.大人施加的力与小孩施加的两个力产生了相同的作用效果
C.两个小孩对水桶施加的力分别为3 N和4 N,则其合力一定为7 N
D.大人的拉力一定等于两个小孩拉力大小之和
√
小孩对水桶施加的两个力与这两个力的合力等效,不是重复作用在水桶上,选项A错误;一个大人或两个小孩都能提起一桶水并保持水桶静止,则大人提水时施加的一个力与小孩提水时施加的两个力产生了相同的作用效果,选项B正确;若两个小孩对水桶施加的力分别为3 N和4 N,则只有当两个分力方向相同时两个力的合力才为7 N,选项C错误;大人的拉力一定等于两个小孩拉力的矢量和,而不等于两个小孩拉力大小之和,故D错误。
4.某人在单杠上做引体向上,在下列选项中,双臂用力最小的是
√
人做引体向上时,双臂的合力大小一定等于人体受到的重力,根据平行四边形定则,两分力夹角越小,双臂用力就越小,故D最大,B最小。故选B。
5.一个重为20 N的物体置于光滑的水平面上,当用一个F=5 N的力竖直向上拉该物体时,如图所示,物体受到的合力为
A.15 N B.25 N
C.20 N D.0
√
由于物体受到的重力大于拉力,则地面对物体有支持力,物体仍然静止,故物体受到的合力为零。故D正确。
6.(2024·重庆市期末考试)某同学研究两个共点力的合成时得出合力F随夹角θ变化的规律如图所示。下列说法正确的是
A.两个分力分别为3 N、4 N
B.1 N≤F≤5 N
C.两个分力分别为3 N、5 N
D.1 N≤F≤4 N
√
由题图可知,两分力夹角为90°时,合力为5 N,则F12+F22=(5 N)2,两分力夹角为180°时,合力为1 N,设F1≥F2,则F1-F2 =1 N,解得F1=4 N,F2=3 N,合力的范围是1 N≤F≤7 N,选项A正确。
7.(2024·陕西咸阳检测)教室里要挂一个城市文化宣传框,假若粘钩的承重能力足够,以下哪种悬挂方式绳上的拉力最小
√
当悬挂的两条绳子长度相等时,绳子上的拉力也相等。由力的合成法则可知,在合力不变的情况下,两条绳子间的夹角越小,绳子上的拉力就越小,故选A。
8.某物体同时受到同一平面内的三个共点力作用,若这三个共点力大小和方向分别如图甲、乙、丙、丁所示(坐标纸中每格边长表示1 N大小的力),则关于该物体受到合力的说法正确的是
A.甲图中物体所受的合外力大小等于4 N
B.乙图中物体所受的合外力大小等于4 N
C.丙图中物体所受的合外力大小等于6 N
D.丁图中物体所受的合外力大小等于6 N
√
题图甲中,先将F1与F3合成,然后再与F2合成,求得合力等于5 N,故A错误;题图乙中,先将F1与F3根据平行四边形定则合成,然后再与F2合成,求得合力等于5 N,故B错误;题图丙中,先将F1与F2根据三角形定则合成,再与F3合成,求得合力为2F3=6 N,故C正确;根据三角形定则,题图丁中合力等于0,故D错误。
9.水平横梁一端插在墙壁内,另一端装有小滑轮B。轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=10 kg的重物,∠CBA=30°,如图所示,则滑轮受到绳子的作用力为(g取10 N/kg)
A.50 N
B.50 N
C.100 N
D.100 N
√
悬挂重物的绳的拉力是F=mg=100 N,故小滑轮受到绳的作用力沿BC、BD方向,夹角为120°,大小都是100 N,故F合=100 N。故选C。
10.如图为颈部牵拉器牵拉颈部肥大患者的示意图。当颈部肥大压迫神经时,需要用颈部牵拉器牵拉颈部,以缓解神经压迫症状。图中牵拉绳为跨过三个光滑小滑轮的同一根绳子,牵拉绳分别沿水平、竖直方向,牵拉物P所受重力为G,不计小滑轮重力,则牵拉器作用在患者头部的合力大小是
A.G
B.2G
C. G
D.3G
√
对颈部牵拉器进行受力分析,如图所示。由平行四边形定则,将力进行合成,则由同一根绳子上的拉力是处处相等的,可得T1=G,T2=2G,那么牵拉器作用在患者头部的合力大小 ,选项C正确。
11.(10分)如图所示,一条小船在河中向正东方向行驶,船上挂起一风帆,帆受侧向风作用,风力大小F1为100 N,方向为东偏南30°,为了使船受到的合力能恰沿正东方向,岸上一人用一根绳子拉船,绳子取向与河岸垂直,求出风力和绳子拉力的合力大小及绳子拉力F2的大小。
答案:50 N 50 N
12.(10分)如图所示,物体受到大小相等的两个拉力F1、F2作用,每个拉力都是200 N,夹角是60°,请在图中画出合力的方向并用计算法求这两个力的合力大小。
答案:方向见解析 200 N
作出力的合成图示如图所示。由于菱形的对角线相互垂直平分,则F=
2F1cos 30°=2×200× N=200 N。
13.(10分)物体受两个大小都等于10 N的拉力作用,且这两个拉力间的夹角为90°,分别用作图法和计算法求这两个力的合力的大小和方向。
答案:14 N 方向与F1夹角为45°
法一:作图法
选取1 cm表示5 N,作出两个力的图示,再以这两力的图示为邻边作平行四边形,如图所示。
用刻度尺量出这两个力所夹对角线的长度约为2.8 cm,则合力大小为F
= ×5 N=14 N。用量角器测出合力F的方向与F1夹角为45°。
法二:计算法
作出力的合成的平行四边形示意图,如图所示。
则该平行四边形为正方形,由几何知识得合力F=
2F1cos 45°=10 N≈14 N
合力F的方向与F1夹角为45°。
返回
4.力的合成
第三章 相互作用
第1课时 力的合成
1.知道合力、分力、力的合成等概念,能从力的作用效果上理解合力和分力。
2.理解共点力,体会力的合成是一种等效替代法。
3.理解平行四边形定则和三角形定则,会用作图法和计算法求合力和分力。
4.知道合力随分力夹角的变化情况,知道合力的取值范围。
素养目标
知识点一 几个力可以用一个力来替代
自主学习
情境导入 如图所示,一个成年人或两个孩子均能提起同一桶水,那么该成年人用的力与两个孩子用的力的作用效果是否相同?
提示:相同
教材梳理 (阅读教材P82完成下列填空)
1.合力、分力:如果力F的作用效果与力F1和F2共同作用的效果______,我们就称F为F1和F2的______,F1和F2为F的______。
2.力的合成:求几个力的______的过程。力的合成是一种__________的方法。
3.共点力:是指作用于物体上________,或者作用在同一物体上且力的________相交于同一点的几个力。
相同
合力
分力
合力
等效替代
同一点
作用线
课堂探究
师生互动 在上述情境导学中:
任务1.成年人用的力与两个孩子用的力是否同时作用在水桶上?
提示:不是
任务2.此时两个孩子用的力可不可以当作成年人用的力的两个分力?
提示:可以
任务3.合力与分力一定是同性质的力吗?
提示:不一定
(多选)关于两个分力F1、F2及它们的合力F,下列说法正确的是
A.合力F一定与F1、F2共同作用产生的效果相同
B.两力F1、F2一定是同种性质的力
C.两力F1、F2一定是同一个物体受的力
D.两力F1、F2与合力F可以是物体同时受到的三个力
例1
√
合力是对两个分力的等效替代,效果相同,故A正确;两个分力可以是同种性质的力,也可以是不同性质的力,故B错误;只有同一个物体受到的力才能合成,分别作用在不同物体上的力不能合成,故C正确;合力与分力不能同时存在,故D错误。
√
如图所示,水平向右运动的物体重力为200 N,物体和水平面之间的动摩擦因数为0.1,在运动过程中,还受到一个水平向左的大小为10 N的拉力作用,则物体受到的摩擦力和合力分别为
A.摩擦力大小为10 N,方向向右;合力大小为10 N,方向向右
B.摩擦力大小为30 N,方向向左;合力大小为30 N,方向向左
C.摩擦力大小为20 N,方向向右;合力大小为10 N,方向向右
D.摩擦力大小为20 N,方向向左;合力大小为30 N,方向向左
例2
√
地面对物体的支持力与物体所受重力平衡,则有N=mg=200 N;物体相对地面向右运动,滑动摩擦力方向向左,大小为f=μN=20 N;物体所受外力的合力方向向左,大小为F合=F+f=20 N+10 N=30 N,故D正确。
1.合力与分力的关系:等效替代。可以是同性质的力,也可以是不同性质的力。
2.合力与分力的大小关系
(1)两分力同向(夹角θ=0°)时,合力最大,F=F1+F2,合力与分力同向。
(2)两分力反向(夹角θ=180°)时,合力最小,F=|F1-F2|,合力的方向与较大的一个分力的方向相同。
(3)合力的取值范围:|F1-F2|≤F≤F1+F2。
针对练1.1654年在德国马德堡市,有人做了著名的马德堡半球实验,各用八匹马组成的两支马队将半球拉开。如图所示,如果用两头大象来代替两支马队,这两个半球也能被拉开。下列说法错误的是
A.一头大象的拉力与八匹马的拉力在作用效果上是相同的
B.一头大象的拉力可以等效替代八匹马的拉力
C.一头大象的拉力是八匹马拉力的分力
D.一头大象的拉力是八匹马拉力的合力
√
一头大象的拉力与八匹马的拉力作用效果相同,都是把两个半球分开,一头大象的拉力可以等效替代八匹马的拉力,即一头大象的拉力是八匹马拉力的合力,故A、B、D正确,C错误。
针对练2.两个共点力的大小分别为F1=10 N,F2=12 N,它们的合力大小不可能等于
A.23 N B.2 N
C.9 N D.22 N
√
当两个力方向相反时,它们的合力最小,则有Fmin=F2-F1=2 N;当两个力方向相同时,它们的合力最大,则有Fmax=F2+F1=22 N,则它们的合力大小范围为2 N≤F≤22 N。故选A。
返回
知识点二 平行四边形定则
自主学习
情境导入 在知识点一情境导入中,成年人用的力F是否与两个孩子用的力F1、F2的大小之和相等?
提示:不相等
教材梳理 (阅读教材P84—P85完成下列填空)
1.平行四边形定则:如果用表示两个共点力F1和F2的线段为邻边作平行四边形,那么合力F的大小和方向就可以用这两个邻边之间的________表示出来。
2.三角形定则:平行四边形的一半是三角形,在求合力的时候,也可以把表示的原来两个力的有向线段首尾相接,然后再从第一个力的始端向第二个力的末端画一条__________,这个__________就可以表示原来两个力的合力。
对角线
有向线段
有向线段
课堂探究
师生互动 自制一个平行四边形模型(如图),结合模型讨论以下问题:
任务1.合力的大小和方向怎样随两个分力夹角的改变而改变?
提示:在两个分力的大小不变的情况下,两分力的夹角越小,合力的大小就越大;两分力的夹角越大,合力的大小越小。
任务2.合力是否总是大于两个分力?合力何时达到最大值?何时达到最小值?
提示:在两个分力的夹角为钝角时,合力的大小可能比分力小;当两个分力的夹角为0°时,合力最大;两个分力的夹角为180°时,合力最小。
师生互动 自制一个平行四边形模型(如图),结合模型讨论以下问题:
任务3.当两个分力之间的夹角分别为0°和180°时,它们的合力如何计算?
提示:当两分力的夹角为0°时,F合=F1+F2;当两个分力的夹角为180°时,F合=|F1-F2|。可见,当两个分力间夹角变化时,合力F合的大小和方向也会随之变化。
角度1 求两个力的合力
上海市的杨浦大桥是我国自行设计建造的双塔双索面叠合梁斜拉桥,如图甲所示。挺拔高耸的208 m主塔似一把利剑直刺苍穹,塔的两侧32对钢索连接主梁,呈扇面展开,如巨型琴弦,正弹奏着巨龙腾飞的奏鸣曲。假设斜拉桥中某对钢索与竖直方向的夹角都是30°,如图乙所示,每根钢索中的拉力都是3×104 N,那么它们对塔柱形成的合力有多大?方向如何?
答案:5.2×104 N 竖直向下
例3
由对称性可知,合力方向一定沿塔柱竖直向下,用两种方法计算合力的大小。
法一:作图法
如图1所示,自O点引两根有向线段OA和OB,
它们跟竖直方向的夹角都为30°,
取单位长度为1×104 N,
则OA和OB的长度都是3个单位长度,
量得对角线OC长约为5.2个单位长度,
所以合力的大小为F=5.2×1×104 N=5.2×104 N,方向竖直向下。
法二:计算法
如图2所示,根据这个平行四边形是一个菱形的特点,连
接AB,交OC于D,则AB与OC互相垂直平分
对于直角三角形AOD,∠AOD=30°,
则有F=2F1cos 30°=2×3×104× N≈5.2×104 N,方
向竖直向下。
角度2 求多个力的合力
(多选)三个共点力,大小分别为4 N、5 N、8 N,夹角任意,它们的合力大小可能是
A.18 N B.8 N
C.1 N D.0
例4
√
√
√
当三力的方向相同时,合力最大,最大为Fmax=4 N+5 N+8 N=17 N。前两个力的合力范围5 N-4 N≤F≤4 N+5 N,即1 N≤F≤9 N,当F=8 N时与第三个力等大反向时,合力为0。即合力的范围0≤F≤17 N,故选BCD。
如图所示,5个力同时作用于一点,5个力大小和方向相当于正六边形的两条边和三条对角线,已知F1 =10 N,则这5个力的合力的大小为
A.30 N
B.40 N
C.50 N
D.60 N
例5
√
解题指导:利用正六边形的几何特性,先将F1与F4合成,再将F2与F5合成,最后求5个力的合力。
如图所示,F1与F4合成时形成以F1和F4为邻作平行四边形,F3为所夹的对角线,即F1与F4的合力为F3,同理可知,F2与F5的合力也为F3,故5个力的合力等于3倍的F3,由几何关系可知F3的大小等于2倍的F1的大小,则5个力的合力大小为6F1=60 N,D正确。
1.作图法
(1)基本思路:
(2)如图所示:用作图法求F1、F2的合力F。
2.计算法
(1)两分力共线时:
①若F1、F2两力同向,则合力F=F1+F2,方向与两力同向。
②若F1、F2两力反向,则合力F=|F1-F2|,方向与两分力中较大者同向。
(2)两分力不共线时:根据平行四边形定则结合几何知识求合力。
常见求合力的三种特殊情况:
3.三个力的合力范围的确定方法
(1)最大值:三个力方向相同时,合力最大,Fmax=F1+F2+F3。
(2)最小值
①若三个力中任何一个力在另外两个力的合力大小范围内,则合力F的最小值为0,即Fmin=0;
②若三个力中任何一个力都不在另外两个力的合力大小范围内,设三个力中最大的一个力的大小为F3,则当大小为F1与F2的两个力方向相同且与大小为F3的力方向相反时,合力最小,Fmin=F3-(F1+F2)。
针对练1.如图所示,大小分别为F1、F2、F3的三个力恰好围成封闭的直角三角形(顶角为直角)。选项图中三个力的合力最大的是
√
由三角形定则可知,题图A中的合力的大小为2F1,题图B中的合力的大小为0,题图C中的合力的大小为2F2,题图D中的合力的大小为2F3,由于F2是直角三角形的斜边,所以F2最大,故合力最大的是C。
针对练2.如图所示,两个人共同用力将一个牌匾拉上墙头。其中一人用了450 N的拉力,另一人用了600 N的拉力,如果这两个人所用拉力的夹角是90°,求它们的合力。
答案:750 N,与较小拉力的夹角为53°
解析:法一:作图法
选择某一标度表示150 N的力。用一个点O代表牌匾,依题意作出两个拉力的图示,再作出力的平行四边形,如图所示。用刻度尺量出平行四边形的对角线长为图示线段的5倍,故合力大小为F=150×5 N= 750 N,用量角器量出合力F与F1的夹角θ= 53°。
法二:计算法
设F1=450 N,F2 =600 N,合力为F
由于F1与F2间的夹角为90°,根据勾股定理得
F= N=750 N,
合力F与F1的夹角θ的正切值 ,所以θ=53°。
返回
随堂演练
1.(人教必修第一册P75T5改编)下列关于合力和分力的说法中,正确的是
A.合力总比任何一个分力都大
B.两个力的合力至少比其中的一个分力大
C.合力的方向只与两分力的夹角有关
D.合力的大小介于两个分力之差的绝对值与两个分力之和之间
√
根据平行四边形定则可知,合力可能比分力大,可能比分力小,也可能与分力相等,A、B错误;根据平行四边形定则可知,合力的方向取决于两分力的大小和方向,C错误;合力的大小取值范围为|F1-F2|≤F≤ F1+F2,即合力的大小介于两个分力之差的绝对值与两个分力之和之间,D正确。
2.两个共点力的大小分别为3 N和4 N,它们的合力不可能是
A.2 N B.4 N
C.6 N D.8 N
√
两力合成时,合力范围为|F1-F2|≤F≤F1+F2,即1 N≤F≤7 N,则合力不可能是8 N。
3.(粤教必修第一册P81T3改编)有两个大小相等的共点力F1和F2。当它们间的夹角为90°时合力为F,则当它们间的夹角为120°时,合力的大小为
A.2F B. F
C. F D. F
√
4.两个人共同拉一头牛,每人的拉力大小和方向如图所示。请用图示法求出牛所受拉力的合力大小。
答案:180 N
由题图可知,F1、F2的图示所选标度为40 N,以
代表F1、F2的有向线段为邻边作平行四边形,F1、
F2所夹的对角线就表示了合力的大小和方向,如
图所示:
用刻度尺量得表示合力的线段长为4.5个标度,合
力为F= ×40 N=180 N。
返回
课 时 测 评
1.(多选)某同学通过以下步骤测出了从一定高度落下的排球对地面的冲击力:将一张白纸铺在水平地面上,把排球在水里弄湿,然后让排球从规定的高度自由落下,并在白纸上留下球的水印。再将印有水印的白纸铺在台秤上。将球放在纸上的水印中心,缓慢地向下压球,使排球与纸接触部分逐渐发生形变直至刚好遮住水印,记下此时台秤的示数即为冲击力的最大值。下列物理学习或研究中用到的方法与该同学的方法相近的是
A.通过平面镜观察桌面的微小形变
B.建立“合力与分力”的概念
C.建立“重心”的概念
D.建立“瞬时速度”的概念
√
√
由题可知,该同学用到了等效替代法。显示微小形变的过程利用了微小放大法,故A错误;建立“合力与分力”的概念用到了等效替代法,故B正确;建立“重心”的概念用到了等效替代法,故C正确;建立“瞬时速度”的概念用到了极限法,故D错误。
2.(多选)关于合力与其两个分力的关系,下列说法正确的是
A.合力的大小可能等于它的某一分力的大小
B.当两个分力的夹角θ逐渐增加时,其合力逐渐变大
C.有两个分力大小分别为7 N和10 N,其合力大小可能为5 N
D.合力一定至少大于其中一个分力
√
当两个分力的夹角θ逐渐增加时,其合力逐渐变小,故B错误;有两个分力大小分别为7 N 和10 N,其合力范围为3~17 N,故C正确;合力与分力遵循平行四边形定则,合力可以大于、等于或小于分力,故A正确,D错误。
√
3.如图所示,一个大人能提起一桶水并保持水桶静止,两个小孩也能共同提起一桶水并保持水桶静止,下列说法正确的是
A.小孩对水桶施加的两个力与这两个力的合力同时作用在水桶上
B.大人施加的力与小孩施加的两个力产生了相同的作用效果
C.两个小孩对水桶施加的力分别为3 N和4 N,则其合力一定为7 N
D.大人的拉力一定等于两个小孩拉力大小之和
√
小孩对水桶施加的两个力与这两个力的合力等效,不是重复作用在水桶上,选项A错误;一个大人或两个小孩都能提起一桶水并保持水桶静止,则大人提水时施加的一个力与小孩提水时施加的两个力产生了相同的作用效果,选项B正确;若两个小孩对水桶施加的力分别为3 N和4 N,则只有当两个分力方向相同时两个力的合力才为7 N,选项C错误;大人的拉力一定等于两个小孩拉力的矢量和,而不等于两个小孩拉力大小之和,故D错误。
4.某人在单杠上做引体向上,在下列选项中,双臂用力最小的是
√
人做引体向上时,双臂的合力大小一定等于人体受到的重力,根据平行四边形定则,两分力夹角越小,双臂用力就越小,故D最大,B最小。故选B。
5.一个重为20 N的物体置于光滑的水平面上,当用一个F=5 N的力竖直向上拉该物体时,如图所示,物体受到的合力为
A.15 N B.25 N
C.20 N D.0
√
由于物体受到的重力大于拉力,则地面对物体有支持力,物体仍然静止,故物体受到的合力为零。故D正确。
6.(2024·重庆市期末考试)某同学研究两个共点力的合成时得出合力F随夹角θ变化的规律如图所示。下列说法正确的是
A.两个分力分别为3 N、4 N
B.1 N≤F≤5 N
C.两个分力分别为3 N、5 N
D.1 N≤F≤4 N
√
由题图可知,两分力夹角为90°时,合力为5 N,则F12+F22=(5 N)2,两分力夹角为180°时,合力为1 N,设F1≥F2,则F1-F2 =1 N,解得F1=4 N,F2=3 N,合力的范围是1 N≤F≤7 N,选项A正确。
7.(2024·陕西咸阳检测)教室里要挂一个城市文化宣传框,假若粘钩的承重能力足够,以下哪种悬挂方式绳上的拉力最小
√
当悬挂的两条绳子长度相等时,绳子上的拉力也相等。由力的合成法则可知,在合力不变的情况下,两条绳子间的夹角越小,绳子上的拉力就越小,故选A。
8.某物体同时受到同一平面内的三个共点力作用,若这三个共点力大小和方向分别如图甲、乙、丙、丁所示(坐标纸中每格边长表示1 N大小的力),则关于该物体受到合力的说法正确的是
A.甲图中物体所受的合外力大小等于4 N
B.乙图中物体所受的合外力大小等于4 N
C.丙图中物体所受的合外力大小等于6 N
D.丁图中物体所受的合外力大小等于6 N
√
题图甲中,先将F1与F3合成,然后再与F2合成,求得合力等于5 N,故A错误;题图乙中,先将F1与F3根据平行四边形定则合成,然后再与F2合成,求得合力等于5 N,故B错误;题图丙中,先将F1与F2根据三角形定则合成,再与F3合成,求得合力为2F3=6 N,故C正确;根据三角形定则,题图丁中合力等于0,故D错误。
9.水平横梁一端插在墙壁内,另一端装有小滑轮B。轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=10 kg的重物,∠CBA=30°,如图所示,则滑轮受到绳子的作用力为(g取10 N/kg)
A.50 N
B.50 N
C.100 N
D.100 N
√
悬挂重物的绳的拉力是F=mg=100 N,故小滑轮受到绳的作用力沿BC、BD方向,夹角为120°,大小都是100 N,故F合=100 N。故选C。
10.如图为颈部牵拉器牵拉颈部肥大患者的示意图。当颈部肥大压迫神经时,需要用颈部牵拉器牵拉颈部,以缓解神经压迫症状。图中牵拉绳为跨过三个光滑小滑轮的同一根绳子,牵拉绳分别沿水平、竖直方向,牵拉物P所受重力为G,不计小滑轮重力,则牵拉器作用在患者头部的合力大小是
A.G
B.2G
C. G
D.3G
√
对颈部牵拉器进行受力分析,如图所示。由平行四边形定则,将力进行合成,则由同一根绳子上的拉力是处处相等的,可得T1=G,T2=2G,那么牵拉器作用在患者头部的合力大小 ,选项C正确。
11.(10分)如图所示,一条小船在河中向正东方向行驶,船上挂起一风帆,帆受侧向风作用,风力大小F1为100 N,方向为东偏南30°,为了使船受到的合力能恰沿正东方向,岸上一人用一根绳子拉船,绳子取向与河岸垂直,求出风力和绳子拉力的合力大小及绳子拉力F2的大小。
答案:50 N 50 N
12.(10分)如图所示,物体受到大小相等的两个拉力F1、F2作用,每个拉力都是200 N,夹角是60°,请在图中画出合力的方向并用计算法求这两个力的合力大小。
答案:方向见解析 200 N
作出力的合成图示如图所示。由于菱形的对角线相互垂直平分,则F=
2F1cos 30°=2×200× N=200 N。
13.(10分)物体受两个大小都等于10 N的拉力作用,且这两个拉力间的夹角为90°,分别用作图法和计算法求这两个力的合力的大小和方向。
答案:14 N 方向与F1夹角为45°
法一:作图法
选取1 cm表示5 N,作出两个力的图示,再以这两力的图示为邻边作平行四边形,如图所示。
用刻度尺量出这两个力所夹对角线的长度约为2.8 cm,则合力大小为F
= ×5 N=14 N。用量角器测出合力F的方向与F1夹角为45°。
法二:计算法
作出力的合成的平行四边形示意图,如图所示。
则该平行四边形为正方形,由几何知识得合力F=
2F1cos 45°=10 N≈14 N
合力F的方向与F1夹角为45°。
返回
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
