教科版高中物理必修第一册 第三章 相互作用素养提升课二共点力平衡中的三类典型问题 课件(共66张PPT)
文档属性
| 名称 | 教科版高中物理必修第一册 第三章 相互作用素养提升课二共点力平衡中的三类典型问题 课件(共66张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-28 19:56:21 | ||
图片预览








文档简介
(共66张PPT)
素养提升课二 共点力平衡中的三类典型问题
第三章 相互作用
1.学会应用整体法和隔离法解决多物体平衡问题。
2.掌握解析法、图解法和相似三角形法解决动态平衡问题。
3.学会处理共点力平衡中的临界、极值问题。
素养目标
提升点一 应用整体法与隔离法分析多物体
平衡问题
1.问题界定:一个平衡系统中涉及两个或两个以上的物体,即为多物体的平衡问题。
2.处理方法:整体法和隔离法
(1)如果不涉及系统内物体间的相互作用力,要优先采用整体法,这样涉及的研究对象少,未知量少,方程少,求解简便;
(2)如果涉及系统内物体间的相互作用力,则必须采用隔离法,对有关物体单独分析。
(3)对于较复杂的问题,往往需要交替使用整体法和隔离法。
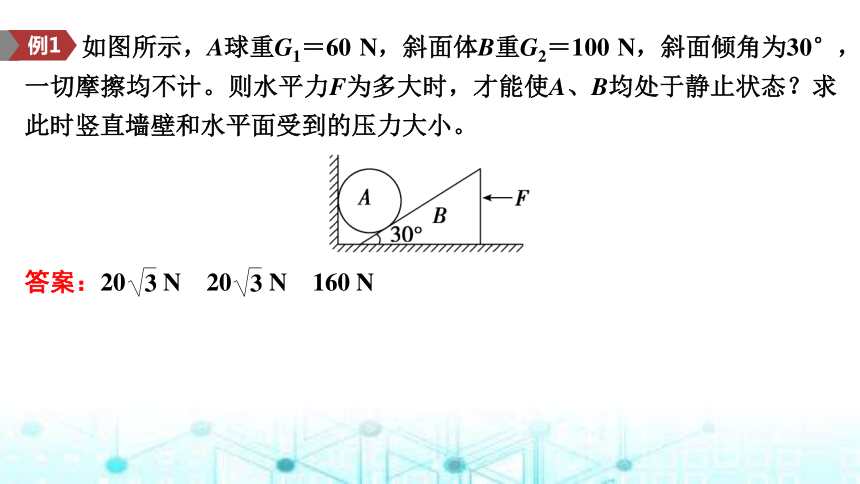
如图所示,A球重G1=60 N,斜面体B重G2=100 N,斜面倾角为30°,一切摩擦均不计。则水平力F为多大时,才能使A、B均处于静止状态?求此时竖直墙壁和水平面受到的压力大小。
答案:20 N 20 N 160 N
例1
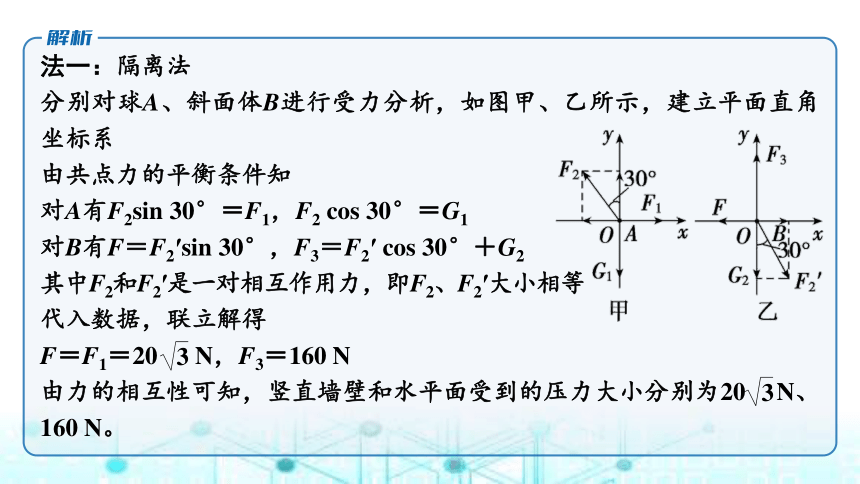
法一:隔离法
分别对球A、斜面体B进行受力分析,如图甲、乙所示,建立平面直角坐标系
由共点力的平衡条件知
对A有F2sin 30°=F1,F2 cos 30°=G1
对B有F=F2′sin 30°,F3=F2′ cos 30°+G2
其中F2和F2′是一对相互作用力,即F2、F2′大小相等
代入数据,联立解得
F=F1=20 N,F3=160 N
由力的相互性可知,竖直墙壁和水平面受到的压力大小分别为20 N、160 N。
法二:整体法
将A、B视为一个整体,该整体处于静止状态,所受合力为零。对整体进行受力分析,如图丙所示,由平衡条件得
F=F1,F3=G1+G2=160 N
再隔离B进行受力分析,如图乙所示,由平衡条件可得
F=F2′sin 30°,F3=F2′cos 30°+G2
联立解得F2′=40 N,F1=F=20 N
由力的相互性可知,竖直墙壁和水平面受到的压力大小分别为20 N、160 N。
针对练1.(多选)(2024·四川眉山期末)如图所示,质量为M的斜面体A放在粗糙水平面上,用轻绳拴住质量为m的小球B置于斜面上,整个系统处于静止状态。已知斜面倾角θ=30°,轻绳与斜面平行且另一端固定在竖直墙面上,不计小球与斜面间的摩擦,则
A.斜面对小球的作用力大小为mg
B.轻绳对小球的作用力大小为 mg
C.水平面对斜面体的支持力大小为(M+m)g
D.斜面体与水平面间的摩擦力大小为 mg
√
√
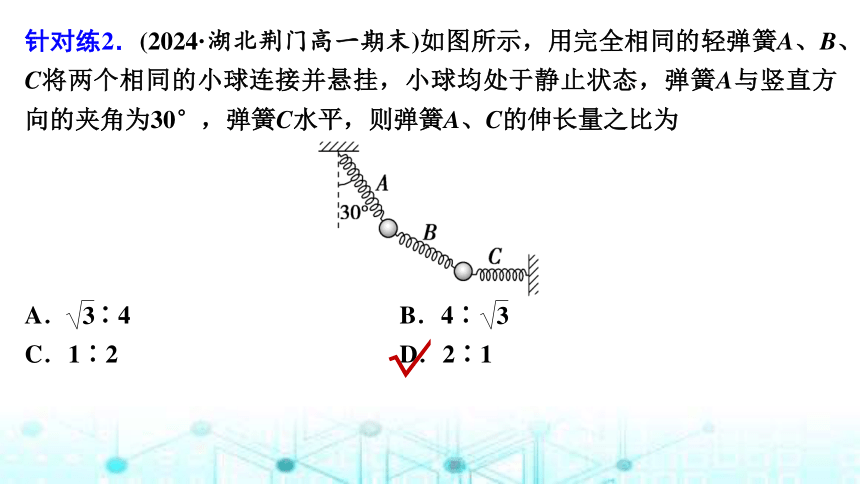
针对练2.(2024·湖北荆门高一期末)如图所示,用完全相同的轻弹簧A、B、C将两个相同的小球连接并悬挂,小球均处于静止状态,弹簧A与竖直方向的夹角为30°,弹簧C水平,则弹簧A、C的伸长量之比为
A. ∶4 B.4∶
C.1∶2 D.2∶1
√
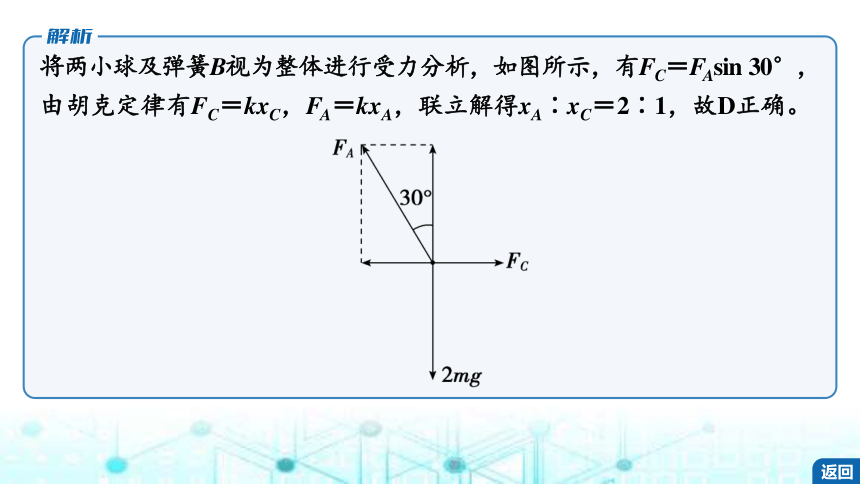
将两小球及弹簧B视为整体进行受力分析,如图所示,有FC=FAsin 30°,
由胡克定律有FC=kxC,FA=kxA,联立解得xA∶xC=2∶1,故D正确。
返回
提升点二 物体的动态平衡问题
1.动态平衡问题的特点
通过控制某一物理量,使其他物理量发生缓慢变化,而变化过程中的任何一个状态都可以看成是平衡状态。
2.处理动态平衡问题常用的方法
解析法 适用于求解直角三角形或正交分解类问题。列出三角函数表达式,然后利用表达式分析力的变化情况的方法
图解法 对研究对象的任一状态进行受力分析,根据平行四边形定则或三角形定则画出不同状态下的力的矢量图,然后根据有向线段的长度变化判断各个力的变化情况。题型特点是:①合力大小和方向不变;②一个分力的方向不变
相似三角形法 适用于求解的是一般形状三角形问题。在受力分析的基础上作出力的平行四边形或三角形,由力的三角形与几何三角形相似,求解问题
角度1 解析法
质量为m的物体用轻绳AB悬挂于天花板上。用水平向左的力F缓慢拉动绳的中点O,如图所示。用T表示绳OA段拉力的大小,在O点向左移动的过程中,拉力F和T的大小怎样变化?
答案:均变大
例2
O点的受力如图所示,由共点力的平衡条件得
F=mg tan θ,T=
当O点向左移动的过程中,θ逐渐变大,则F逐渐变大,T逐渐变大。
针对练.(多选)(2024·浙江绍兴高一期末)如图所示,铁板AB与水平地面垂直,一块磁铁吸附在铁板左侧。现使铁板绕A点缓慢逆时针转动到与水平方向成θ角(θ>0°),在此过程中磁铁始终相对铁板静止。下列说法中正确的是
A.磁铁所受的合外力逐渐减小
B.磁铁始终受到四个力的作用
C.铁板对磁铁的弹力逐渐减小
D.铁板受到的摩擦力逐渐减小
√
√
√
铁板绕A点缓慢逆时针转动,认为是个动态平衡过程,磁铁始终处于平衡状态,所以所受合外力始终为零,A错误;磁铁受到重力、铁板对其吸引力、弹力、摩擦力四个作用力,B正确;受力分析如图所示,则有f=G sin θ,N=F引-G cos θ,随着θ角减小,铁板对磁铁的弹力逐渐减小,摩擦力逐渐减小,C、D正确。
角度2 图解法
如图所示,斜面与水平面、斜面与挡板间的夹角均为30°,一小球放置在斜面与挡板之间,挡板对小球的弹力为N1,斜面对小球的弹力为N2,以挡板与斜面连接点所形成的水平直线为轴,将挡板从图示位置开始逆时针缓慢地转到水平位置,不计摩擦,在此过程中
A.N1始终减小,N2始终减小
B.N1始终增大,N2始终增大
C.N1始终减小,N2先减小后增大
D.N1先减小后增大,N2始终减小
例3
√
对小球受力分析如图所示,将N1与N2合成,其合力与重力等大反向。挡板转动时,挡板给球的弹力N1与斜面给球的弹力N2的合力大小与方向不变,其中N2的方向不变,挡板逆时针转动过程中,N1的方向变化如图中a、b、c的规律变化,为满足平行四边形定则,其先变小后变大,其中挡板与斜面垂直时为最小。与此对应,N2一直减小。故D正确。
变式拓展.如果仅将【例3】中“挡板从图示位置开始逆时针缓慢地转到水平位置”改为“挡板从图示位置开始逆时针缓慢地转到垂直于斜面位置”,则应选_____。(选项同例3)
挡板从题图示位置开始逆时针缓慢地转到垂直于斜面位置过程中,N1始终减小,没有增大的过程,N2始终减小,故选A。
A
针对练.(多选)(2024·河南南阳高一期末)用绳OD悬挂一个重力为G的物体,O位于半圆形支架的圆心,绳OA、OB的悬点A、B在支架上。悬点A固定不动,结点O保持不动,开始时,OB水平,将悬点B从图中所示位置沿支架逐渐移动到C点的过程中,下列说法正确的是
A.绳OA的拉力逐渐减小
B.绳OA的拉力逐渐增大
C.绳OB的拉力一直减小
D.绳OB的拉力先减小后增大
√
√
法一:图解法之平行四边形法
在支架上选取三个点B1、B2、B3,当悬点B分别移动
到B1、B2、B3时,OA、OB上的拉力分别为TA1、TA2、
TA3和TB1、TB2、TB3,由于绳子OD对O点的拉力TD =
G,结点O始终处于平衡状态,则将TD沿AO、BO方向
分解,如图1所示,分力的大小分别等于绳子OA、OB
对O点的拉力大小,分力的方向分别与绳子OA、OB对O点的拉力方向相反,从图中可以直观地看出,TA=TA′逐渐减小,且方向不变;而TB=TB′先减小后增大,且方向不断改变,当TB与TA垂直时,TB最小。故A、D正确。
法二:图解法之矢量三角形法
将表示O点所受三个力的有向线段首尾相接,构成的矢量三角形如图2所示,将悬点B从题图中所示位置逐渐移动到C点的过程中,绳OB上的拉力TB与水平方向的夹角α从0°逐渐增大到90°,根据矢量三角形可知绳OA的拉力TA逐渐减小到0,绳OB上的拉力TB先减小后增大到TB=TD=G。故A、D正确。
角度3 相似三角形法
如图所示,光滑半球面上的小球被一通过定滑轮的力F由底端缓慢拉到顶端的过程中,试分析绳的拉力F及半球面对小球的支持力N的变化情况。
答案:减小 不变
例4
作出小球的受力示意图,如图所示
设半球面的半径为R,定滑轮到半球面最高点的距离为h,定滑轮与小球间绳长为L,根据三角形相似得
解得绳中的张力F=mg
半球面对小球的支持力N=mg
由于在拉动过程中h、R不变,L变小,故F减小,N不变。
针对练.(2024·甘肃兰州一中期末)如图所示,不计重力的轻杆AB可以A为轴在竖直平面内转动,其B端系一重物G。另用一根跨过滑轮的轻绳系住B端,并在绳的另一端作用外力F。在图中θ角由30°增大到150°的过程中,AB杆所受轴处作用力的变化情况是
A.始终不变 B.先变小后变大
C.先变大后变小 D.不断减小
√
设AB杆所受轴处作用力为T,对B端进行受力分析如图所示。B端受三力平衡,三力围成的矢量三角形与△ABC始终相似,根据相似比相等
有 由于重力G与AC的长度始终不变,故相似比不变,杆AB的
长度也不变,故θ角增大的过程中,T也不变,A正确。
返回
提升点三 平衡中的临界、极值问题
1.临界问题
(1)问题界定:物体所处平衡状态将要发生变化的状态为临界状态,涉及临界状态的问题为临界问题。
(2)问题特点:
①当某物理量发生变化时,会引起其他几个物理量的变化。
②注意某现象“恰好出现”或“恰好不出现”的条件。
(3)分析方法:基本方法是假设推理法,即先假设某种情况成立,然后根据平衡条件及有关知识进行论证、求解。
2.极值问题
(1)问题界定:物体平衡的极值问题,一般指在力的变化过程中涉及力的最大值和最小值的问题。
(2)分析方法:
①解析法:根据物体平衡的条件列出方程,在解方程时,采用数学知识求极值或者根据物理临界条件求极值。
②图解法:根据物体平衡的条件作出力的矢量图,画出平行四边形或者矢量三角形进行动态分析,确定最大值或最小值。
(2024·河南洛阳高一月考)如图所示,斜面与水平面的夹角为37°,物体A质量为2 kg,与斜面间动摩擦因数为0.5,求:
(1)A受到斜面的支持力多大?
答案:16 N
例5
对A进行受力分析如图所示
根据正交分解可知
N=mAgcos 37°=16 N。
(2)若要使A在斜面上静止,求物体B质量的最大值和最小值(sin 37°=0.6,cos 37°=0.8,g=10 N/kg,最大静摩擦力等于滑动摩擦力)。
答案:2 kg 0.4 kg
根据题意,物体A与斜面之间的最大静摩擦力fmax=f滑=μN=0.5×16 N=8 N
当物体受到的摩擦力等于最大静摩擦且方向沿斜面向上时,拉力T最小,根据受力平衡有T1+fmax=mAgsin 37°;当物体受到的摩擦力等于最大静摩擦力且方向沿斜面向下时,拉力T最大,根据受力平衡有T2=fmax+mAgsin 37°
同时物体B也处于平衡状态,由平衡条件有T1=mB1g,
T2=mB2g
联立并代入数据可得T1=4 N,T2 =20 N
则物体B质量的最小值为mB1=0.4 kg
最大值为mB2 =2 kg。
针对练1.如图所示,三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物,其中OB是水平的,A端、B端分别固定在水平天花板上和竖直墙上。若逐渐增加C端所挂重物的质量,则最先断的绳是
A.必定是OA
B.必定是OB
C.必定是OC
D.可能是OB,也可能是OC
√
C端悬挂重物,它对O点的拉力等于重物所受的重力G。OC绳的拉力产生两个效果:使OB在O点受到水平向左的力F1;使OA在O点受到沿绳子方向斜向下的力F2。F1、F2是G的两个分力。由平行四边形定则可作出力的分解图如图所示,由于三段绳所能承受的最大拉力相同,当逐渐增大所挂重物的质量时,从图中可知,表示F2的有向线段最长,分力F2最大,故OA绳最先断,A正确。
针对练2.一人站在斜坡上,推着一个重力大小为G的大雪球,若雪球刚好处在一倾角为θ的光滑斜面上,且始终处于静止状态。此人的推力通过雪球的球心,则
A.此人的推力最小值为G tan θ
B.此人的推力最小值为G sin θ
C.此人的推力最大值为
D.此人的推力最大值
√
雪球受力分析如图所示,受重力G、弹力N、推力F。因雪球静止在斜面上,由平衡条件及平行四边形定则知,推力和支持力合力大小等于重力。由平行四边形定则知,当推力由水平转至沿斜面向上时最小,为G sin θ;推力由水平向下转时无穷大,即无最大值,故B正确。
返回
随堂演练
1.如图所示,放在水平地面上的物块,受到一个与水平方向成α角斜向下方的力F的作用,该物块恰好在水平地面上做匀速直线运动。如果保持该推力F的大小不变,而使力F与水平方向的夹角α变小,那么,地面受到的压力N和物块受到的摩擦力f的变化情况是
A.N变小,f变大 B.N变大,f变小
C.N变大,f变大 D.N变小,f变小
√
物块受力分析如图所示,有N′=G+F sin α,f=μN′。当力F与水平方向的夹角α变小时,地面对物块的支持力N′变小,动摩擦因数不变,物块受到的摩擦力f变小,根据牛顿第三定律可得,地面受到的压力N变小,D正确。
2.(多选)(人教必修第一册P79T3改编)某同学在实验室进行力学实验,如图所示,物体质量为m,用细绳OC悬在O点。现用同样材料的细绳AB绑住绳OC上的A点,用水平力F缓慢牵引A点,到图中虚线位置某绳刚好先断,相关实验结论符合事实的是
A.OA绳承受的力先增大后减小
B.若三根绳能承受的最大拉力相同,则OA绳先断
C.OA绳和AB绳的合力不变
D.AB绳受到的拉力逐渐增大
√
√
√
结点A下方AC绳始终受到向下大小为mg的力作用,还受到水平向右的拉力F作用及OA绳的拉力T作用,由三角形定则,可把三个力平移首尾依次相连,如图所示。当A点缓慢升高的过程中,拉力T不断逆时针转动,但始终与F及mg构成直角三角形,由图可知,OA绳承受的拉力T始终在增大,AB绳受到的拉力F逐渐增大。由于OA绳的拉力T作为三角形的斜边,拉力始终最大,会先达到能承受的最大拉力,若三根绳能承受的最大拉力相同,则OA绳会先断,A错误,B、D正确。OA绳和AB绳的合力始终等于物体的重力mg,故保持不变,C正确。
3.(多选)如图所示,轻质细杆AO、BO左端固定在竖直墙壁上,右端通过垂直于纸面的光滑轴连接于O点,AO水平,BO与竖直方向的夹角为θ。将质量为m的物体用轻绳悬挂在O点,物体静止时,若细杆AO对O点的拉力沿OA方向、大小为F1,细杆BO对O点的支持力沿BO方向、大小为F2,重力加速度为g,则
A.F1=mg tan θ B.F1=mg cos θ
C.F2= D.F2=
√
√
对O点受力分析,如图所示,根据共点力平衡可知F=T=mg,根据数
学知识可得F1=mg tan θ,F2= ,A、D正确,B、C错误。
4.用轻质细线把两个质量未知的小球悬挂起来,如图所示。对小球a持续施加一个水平向左的恒力,并对小球b持续施加一个水平向右的同样大小的恒力,最后达到平衡状态。下列选项中表示平衡状态的图可能是
√
将两球和两球之间的细线看成一个整体,对整体受力分析如图甲所示。根据平衡条件可知整体受到a球上方的细线的拉力F线的大小等于a、b的重力大小之和,方向沿竖直方向,故此细线必定沿竖直方向;对b球受力分析如图乙所示。根据平衡条件可知b球上方细线的拉力F线的大小等于b球重力与恒力F的合力,方向斜向左上方,故a、b球之间的线必定斜向左上方,故A正确。
返回
课 时 测 评
1.(多选)(2024·河南期末)某小城街道两旁的仿古路灯如图所示,灯笼悬挂在灯柱上,若风沿水平方向由左向右吹来,且风力缓慢增大,则
A.灯柱对灯笼的作用力逐渐减小
B.灯柱对灯笼的作用力逐渐增大
C.灯柱对灯笼的作用力与竖直方向的夹角逐渐增大
D.灯柱对灯笼的作用力与竖直方向的夹角逐渐减小
√
√
对灯笼受力分析,灯笼所受三力可构成力的矢量三角形,如图所示,可知风力F1越来越大时,灯柱对灯笼的作用力F2逐渐增大,灯柱对灯笼的作用力与竖直方向的夹角逐渐增大,A、D错误,B、C正确。
2.(2024·广东广州期末)如图所示,清洗楼房玻璃的工人常用一根悬绳将自己悬在空中,悬绳与竖直墙壁呈一定夹角,悬绳对工人的拉力大小为T,墙壁对工人的弹力大小为N,忽略一切摩擦。若缓慢减小悬绳的长度,下列说法正确的是
A.T减小,N减小
B.T减小,N增大
C.T与N的合力变大
D.T与N的合力不变
√
工人受到悬绳的拉力T、弹力N、重力G。在三个力的作用下平衡,则当缓慢减小悬绳的长度时,悬绳与墙壁的夹角逐渐增大,受力如图所示,即悬绳的拉力T从T1经T2逐渐变为T3,由此可知悬绳拉力T在逐渐变大,弹力N在逐渐增大,选项A、B错误;工人受力平衡,则T与N的合力与重力大小相等、方向相反,不会发生变化,选项C错误,D正确。
3.(多选)(2024·安徽师范大学附属中学期末)如图所示,用与竖直方向成θ角(θ<45°)的倾斜轻绳a和水平轻绳b共同固定一个小球,这时绳b的拉力为T1。现保持小球在原位置不动,使绳b在原竖直平面内沿逆时针方向转过θ角并固定,绳b的拉力变为T2;再转过θ角并固定,绳b的拉力变为T3,则
A.T1=T3>T2 B.T1<T2<T3
C.T1=T3<T2 D.随绳b转动,绳a的拉力减小
√
√
以小球为研究对象,小球受到重力、绳a的拉力T、绳b的拉力T1。根据平衡条件得知,T和T1的合力方向竖直向上,大小与重力相等,保持不变,作出绳b在三个不同位置时的拉力,如图所示,可得T1=T3>T2,且绳a的拉力不断减小,故A、D正确。
4.如图所示,固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔,质量为m的小球套在圆环上,一根细线的下端系着小球,上端穿过小孔用手拉住。现拉动细线,使小球沿圆环缓慢上移。在移动过程中手对线的拉力F和圆环对小球的弹力N的大小变化情况是
A.F减小,N不变 B.F不变,N减小
C.F不变,N增大 D.F增大,N减小
√
小球沿圆环缓慢上移可看作动态平衡,对小球进行受力分析,小球受重力G、拉力F′、弹力N三个力,其中F′=F。G与N的合力与F′等大反
向,如图所示,可知△OAB~△DCA,则 当A点上移时,圆
环半径R不变,AB长度减小,故F′=F减小,N不变,A正确。
5.(多选)倾角为α、质量为M的斜面体静止在水平桌面上,质量为m的木块静止在斜面体上。下列结论正确的是
A.木块受到的摩擦力大小是mg sin α
B.木块对斜面体的压力大小是mg sin α
C.桌面对斜面体的摩擦力大小是mgsin αcos α
D.桌面对斜面体的支持力大小是(M+m)g
√
√
以木块为研究对象,如图甲所示,有f=mg sin α,N=mg cos α,故A正确,B错误;以木块与斜面体所组成的整体为研究对象,如图乙所示,有f桌=0,N桌=(M+m)g,故C错误,D正确。
6.(2023·福建龙岩期末)如图所示,A、B两物体的质量分别为mA、mB,且mA>mB,整个系统处于静止状态,滑轮的质量和一切摩擦均不计,如果绳的一端由Q点缓慢地向左移到P点,整个系统重新静止后,绳的拉力F和绳与水平方向的夹角θ的变化情况是
A.F变大,θ角变大 B.F变小,θ角变小
C.F不变,θ角不变 D.F不变,θ角变小
√
重新静止后,绳的拉力F仍等于A物体的重力,B物体所受绳的拉力的合力与B物体的重力等大、反向,所以有2mAg sin θ=mBg,即sin θ= ,所以θ不变,C正确。
7.(多选)(2024·广东清远检测)如图所示,物体P静止于固定的斜面上,P的上表面水平。现把物体Q轻轻地叠放在P上,则(静大静摩擦力等于将动摩擦力)
A.P向下滑动 B.P静止不动
C.P所受的合外力增大 D.P与斜面间的静摩擦力增大
√
√
P在斜面上处于静止状态,设P的质量为M,斜面的倾角为θ,斜面与P之间的动摩擦因数为μ0,则有μ0Mgcos θ≥Mg sin θ,即μ≥tan θ;当加上一个质量为m的物体Q后,有μ0(M+m)g cos θ≥(M+m)g sin θ,因此P仍处于静止状态,选项A错误,B正确。由于P处于静止状态,合外力始终为零,选项C错误。由平衡条件知,P与斜面间的静摩擦力由Mg sin θ变为(M+m)g sin θ,选项D正确。
8.(2024·重庆市第十一中学期末)一横梁起重机移动货物时因出现故障而失去动力,工作人员在货物上作用一水平恒力,使货物和起重机一起缓慢向右移动,如图所示,已知起重机的质量为m1=1 kg,货物的质量为m2=3 kg,绳索与水平轨道间的夹角为θ=53°,绳索的质量不计(sin 53°=0.8,cos 53°=0.6),则水平横梁对起重机的阻力大小与横梁受到的压力大小的比值为
√
对货物和起重机分别受力分析,如图所示,对货物有T2sin θ=m2g,T2cos θ=F,对起重机有N=m1g+T1sin θ,f=T1cos θ,T1=T2,所以
有 选项A正确。
9.(10分)一盏电灯的重力为G,悬于天花板上A点,在电线O处系一细线OB,使电线OA与竖直方向的夹角为β=30°,如图所示。现保持β角不变,缓慢调整OB方向至OB线上拉力最小为止,此时OB与水平方向的夹角α等于多少?最小拉力是多少?
答案:30°
对电灯受力分析如图所示,据三力平衡特点可知OA、OB对O点的作用力TA、TB的合力T与G等大反向,即T=G
在△OTBT中,∠TOTB =90°-α
又∠OTTB=∠TOA=β,
故∠OTBT=180°-(90°-α)-β=90°+α-β
由正弦定理得=
联立解得TB=
因β不变,故当α=β=30°时,TB最小,且TB=G sin β= 。
10.(10分)如图甲所示,由两根短杆组成的一个自锁定起重吊钩,将它放入被吊的空罐内,使其张开一定的夹角压紧罐壁,内部结构如图乙所示,当钢绳向上提起时,两杆对罐壁越压越紧,摩擦力足够大时,就能将空罐提升起来,罐越重,短杆提供的压力越大,称为“自锁定吊钩”。若罐的质量为m,重力加速度为g,短杆与竖直方向的夹角θ=60°,求吊起该空罐时,每根短杆对罐壁的压力大小。(短杆的质量不计)
答案: mg
如图(a)所示,从整体来看,钢绳的拉力F=G,它可以分解为沿杆方向的两个大小相等的分力F′和F″,F′通过杆作用于罐壁,F′可分解为竖直向上的分力F1和垂直于罐壁的分力F2,如图(b)所示。由θ=60°及菱形知识得F′=F=G。
由图(b)可知F2=F′sin θ= 又F′垂直于罐壁的分力等于一根
短杆对罐壁的压力,所以每根短杆对罐壁的压力大小为 mg。
返回
素养提升课二 共点力平衡中的三类典型问题
第三章 相互作用
1.学会应用整体法和隔离法解决多物体平衡问题。
2.掌握解析法、图解法和相似三角形法解决动态平衡问题。
3.学会处理共点力平衡中的临界、极值问题。
素养目标
提升点一 应用整体法与隔离法分析多物体
平衡问题
1.问题界定:一个平衡系统中涉及两个或两个以上的物体,即为多物体的平衡问题。
2.处理方法:整体法和隔离法
(1)如果不涉及系统内物体间的相互作用力,要优先采用整体法,这样涉及的研究对象少,未知量少,方程少,求解简便;
(2)如果涉及系统内物体间的相互作用力,则必须采用隔离法,对有关物体单独分析。
(3)对于较复杂的问题,往往需要交替使用整体法和隔离法。
如图所示,A球重G1=60 N,斜面体B重G2=100 N,斜面倾角为30°,一切摩擦均不计。则水平力F为多大时,才能使A、B均处于静止状态?求此时竖直墙壁和水平面受到的压力大小。
答案:20 N 20 N 160 N
例1
法一:隔离法
分别对球A、斜面体B进行受力分析,如图甲、乙所示,建立平面直角坐标系
由共点力的平衡条件知
对A有F2sin 30°=F1,F2 cos 30°=G1
对B有F=F2′sin 30°,F3=F2′ cos 30°+G2
其中F2和F2′是一对相互作用力,即F2、F2′大小相等
代入数据,联立解得
F=F1=20 N,F3=160 N
由力的相互性可知,竖直墙壁和水平面受到的压力大小分别为20 N、160 N。
法二:整体法
将A、B视为一个整体,该整体处于静止状态,所受合力为零。对整体进行受力分析,如图丙所示,由平衡条件得
F=F1,F3=G1+G2=160 N
再隔离B进行受力分析,如图乙所示,由平衡条件可得
F=F2′sin 30°,F3=F2′cos 30°+G2
联立解得F2′=40 N,F1=F=20 N
由力的相互性可知,竖直墙壁和水平面受到的压力大小分别为20 N、160 N。
针对练1.(多选)(2024·四川眉山期末)如图所示,质量为M的斜面体A放在粗糙水平面上,用轻绳拴住质量为m的小球B置于斜面上,整个系统处于静止状态。已知斜面倾角θ=30°,轻绳与斜面平行且另一端固定在竖直墙面上,不计小球与斜面间的摩擦,则
A.斜面对小球的作用力大小为mg
B.轻绳对小球的作用力大小为 mg
C.水平面对斜面体的支持力大小为(M+m)g
D.斜面体与水平面间的摩擦力大小为 mg
√
√
针对练2.(2024·湖北荆门高一期末)如图所示,用完全相同的轻弹簧A、B、C将两个相同的小球连接并悬挂,小球均处于静止状态,弹簧A与竖直方向的夹角为30°,弹簧C水平,则弹簧A、C的伸长量之比为
A. ∶4 B.4∶
C.1∶2 D.2∶1
√
将两小球及弹簧B视为整体进行受力分析,如图所示,有FC=FAsin 30°,
由胡克定律有FC=kxC,FA=kxA,联立解得xA∶xC=2∶1,故D正确。
返回
提升点二 物体的动态平衡问题
1.动态平衡问题的特点
通过控制某一物理量,使其他物理量发生缓慢变化,而变化过程中的任何一个状态都可以看成是平衡状态。
2.处理动态平衡问题常用的方法
解析法 适用于求解直角三角形或正交分解类问题。列出三角函数表达式,然后利用表达式分析力的变化情况的方法
图解法 对研究对象的任一状态进行受力分析,根据平行四边形定则或三角形定则画出不同状态下的力的矢量图,然后根据有向线段的长度变化判断各个力的变化情况。题型特点是:①合力大小和方向不变;②一个分力的方向不变
相似三角形法 适用于求解的是一般形状三角形问题。在受力分析的基础上作出力的平行四边形或三角形,由力的三角形与几何三角形相似,求解问题
角度1 解析法
质量为m的物体用轻绳AB悬挂于天花板上。用水平向左的力F缓慢拉动绳的中点O,如图所示。用T表示绳OA段拉力的大小,在O点向左移动的过程中,拉力F和T的大小怎样变化?
答案:均变大
例2
O点的受力如图所示,由共点力的平衡条件得
F=mg tan θ,T=
当O点向左移动的过程中,θ逐渐变大,则F逐渐变大,T逐渐变大。
针对练.(多选)(2024·浙江绍兴高一期末)如图所示,铁板AB与水平地面垂直,一块磁铁吸附在铁板左侧。现使铁板绕A点缓慢逆时针转动到与水平方向成θ角(θ>0°),在此过程中磁铁始终相对铁板静止。下列说法中正确的是
A.磁铁所受的合外力逐渐减小
B.磁铁始终受到四个力的作用
C.铁板对磁铁的弹力逐渐减小
D.铁板受到的摩擦力逐渐减小
√
√
√
铁板绕A点缓慢逆时针转动,认为是个动态平衡过程,磁铁始终处于平衡状态,所以所受合外力始终为零,A错误;磁铁受到重力、铁板对其吸引力、弹力、摩擦力四个作用力,B正确;受力分析如图所示,则有f=G sin θ,N=F引-G cos θ,随着θ角减小,铁板对磁铁的弹力逐渐减小,摩擦力逐渐减小,C、D正确。
角度2 图解法
如图所示,斜面与水平面、斜面与挡板间的夹角均为30°,一小球放置在斜面与挡板之间,挡板对小球的弹力为N1,斜面对小球的弹力为N2,以挡板与斜面连接点所形成的水平直线为轴,将挡板从图示位置开始逆时针缓慢地转到水平位置,不计摩擦,在此过程中
A.N1始终减小,N2始终减小
B.N1始终增大,N2始终增大
C.N1始终减小,N2先减小后增大
D.N1先减小后增大,N2始终减小
例3
√
对小球受力分析如图所示,将N1与N2合成,其合力与重力等大反向。挡板转动时,挡板给球的弹力N1与斜面给球的弹力N2的合力大小与方向不变,其中N2的方向不变,挡板逆时针转动过程中,N1的方向变化如图中a、b、c的规律变化,为满足平行四边形定则,其先变小后变大,其中挡板与斜面垂直时为最小。与此对应,N2一直减小。故D正确。
变式拓展.如果仅将【例3】中“挡板从图示位置开始逆时针缓慢地转到水平位置”改为“挡板从图示位置开始逆时针缓慢地转到垂直于斜面位置”,则应选_____。(选项同例3)
挡板从题图示位置开始逆时针缓慢地转到垂直于斜面位置过程中,N1始终减小,没有增大的过程,N2始终减小,故选A。
A
针对练.(多选)(2024·河南南阳高一期末)用绳OD悬挂一个重力为G的物体,O位于半圆形支架的圆心,绳OA、OB的悬点A、B在支架上。悬点A固定不动,结点O保持不动,开始时,OB水平,将悬点B从图中所示位置沿支架逐渐移动到C点的过程中,下列说法正确的是
A.绳OA的拉力逐渐减小
B.绳OA的拉力逐渐增大
C.绳OB的拉力一直减小
D.绳OB的拉力先减小后增大
√
√
法一:图解法之平行四边形法
在支架上选取三个点B1、B2、B3,当悬点B分别移动
到B1、B2、B3时,OA、OB上的拉力分别为TA1、TA2、
TA3和TB1、TB2、TB3,由于绳子OD对O点的拉力TD =
G,结点O始终处于平衡状态,则将TD沿AO、BO方向
分解,如图1所示,分力的大小分别等于绳子OA、OB
对O点的拉力大小,分力的方向分别与绳子OA、OB对O点的拉力方向相反,从图中可以直观地看出,TA=TA′逐渐减小,且方向不变;而TB=TB′先减小后增大,且方向不断改变,当TB与TA垂直时,TB最小。故A、D正确。
法二:图解法之矢量三角形法
将表示O点所受三个力的有向线段首尾相接,构成的矢量三角形如图2所示,将悬点B从题图中所示位置逐渐移动到C点的过程中,绳OB上的拉力TB与水平方向的夹角α从0°逐渐增大到90°,根据矢量三角形可知绳OA的拉力TA逐渐减小到0,绳OB上的拉力TB先减小后增大到TB=TD=G。故A、D正确。
角度3 相似三角形法
如图所示,光滑半球面上的小球被一通过定滑轮的力F由底端缓慢拉到顶端的过程中,试分析绳的拉力F及半球面对小球的支持力N的变化情况。
答案:减小 不变
例4
作出小球的受力示意图,如图所示
设半球面的半径为R,定滑轮到半球面最高点的距离为h,定滑轮与小球间绳长为L,根据三角形相似得
解得绳中的张力F=mg
半球面对小球的支持力N=mg
由于在拉动过程中h、R不变,L变小,故F减小,N不变。
针对练.(2024·甘肃兰州一中期末)如图所示,不计重力的轻杆AB可以A为轴在竖直平面内转动,其B端系一重物G。另用一根跨过滑轮的轻绳系住B端,并在绳的另一端作用外力F。在图中θ角由30°增大到150°的过程中,AB杆所受轴处作用力的变化情况是
A.始终不变 B.先变小后变大
C.先变大后变小 D.不断减小
√
设AB杆所受轴处作用力为T,对B端进行受力分析如图所示。B端受三力平衡,三力围成的矢量三角形与△ABC始终相似,根据相似比相等
有 由于重力G与AC的长度始终不变,故相似比不变,杆AB的
长度也不变,故θ角增大的过程中,T也不变,A正确。
返回
提升点三 平衡中的临界、极值问题
1.临界问题
(1)问题界定:物体所处平衡状态将要发生变化的状态为临界状态,涉及临界状态的问题为临界问题。
(2)问题特点:
①当某物理量发生变化时,会引起其他几个物理量的变化。
②注意某现象“恰好出现”或“恰好不出现”的条件。
(3)分析方法:基本方法是假设推理法,即先假设某种情况成立,然后根据平衡条件及有关知识进行论证、求解。
2.极值问题
(1)问题界定:物体平衡的极值问题,一般指在力的变化过程中涉及力的最大值和最小值的问题。
(2)分析方法:
①解析法:根据物体平衡的条件列出方程,在解方程时,采用数学知识求极值或者根据物理临界条件求极值。
②图解法:根据物体平衡的条件作出力的矢量图,画出平行四边形或者矢量三角形进行动态分析,确定最大值或最小值。
(2024·河南洛阳高一月考)如图所示,斜面与水平面的夹角为37°,物体A质量为2 kg,与斜面间动摩擦因数为0.5,求:
(1)A受到斜面的支持力多大?
答案:16 N
例5
对A进行受力分析如图所示
根据正交分解可知
N=mAgcos 37°=16 N。
(2)若要使A在斜面上静止,求物体B质量的最大值和最小值(sin 37°=0.6,cos 37°=0.8,g=10 N/kg,最大静摩擦力等于滑动摩擦力)。
答案:2 kg 0.4 kg
根据题意,物体A与斜面之间的最大静摩擦力fmax=f滑=μN=0.5×16 N=8 N
当物体受到的摩擦力等于最大静摩擦且方向沿斜面向上时,拉力T最小,根据受力平衡有T1+fmax=mAgsin 37°;当物体受到的摩擦力等于最大静摩擦力且方向沿斜面向下时,拉力T最大,根据受力平衡有T2=fmax+mAgsin 37°
同时物体B也处于平衡状态,由平衡条件有T1=mB1g,
T2=mB2g
联立并代入数据可得T1=4 N,T2 =20 N
则物体B质量的最小值为mB1=0.4 kg
最大值为mB2 =2 kg。
针对练1.如图所示,三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物,其中OB是水平的,A端、B端分别固定在水平天花板上和竖直墙上。若逐渐增加C端所挂重物的质量,则最先断的绳是
A.必定是OA
B.必定是OB
C.必定是OC
D.可能是OB,也可能是OC
√
C端悬挂重物,它对O点的拉力等于重物所受的重力G。OC绳的拉力产生两个效果:使OB在O点受到水平向左的力F1;使OA在O点受到沿绳子方向斜向下的力F2。F1、F2是G的两个分力。由平行四边形定则可作出力的分解图如图所示,由于三段绳所能承受的最大拉力相同,当逐渐增大所挂重物的质量时,从图中可知,表示F2的有向线段最长,分力F2最大,故OA绳最先断,A正确。
针对练2.一人站在斜坡上,推着一个重力大小为G的大雪球,若雪球刚好处在一倾角为θ的光滑斜面上,且始终处于静止状态。此人的推力通过雪球的球心,则
A.此人的推力最小值为G tan θ
B.此人的推力最小值为G sin θ
C.此人的推力最大值为
D.此人的推力最大值
√
雪球受力分析如图所示,受重力G、弹力N、推力F。因雪球静止在斜面上,由平衡条件及平行四边形定则知,推力和支持力合力大小等于重力。由平行四边形定则知,当推力由水平转至沿斜面向上时最小,为G sin θ;推力由水平向下转时无穷大,即无最大值,故B正确。
返回
随堂演练
1.如图所示,放在水平地面上的物块,受到一个与水平方向成α角斜向下方的力F的作用,该物块恰好在水平地面上做匀速直线运动。如果保持该推力F的大小不变,而使力F与水平方向的夹角α变小,那么,地面受到的压力N和物块受到的摩擦力f的变化情况是
A.N变小,f变大 B.N变大,f变小
C.N变大,f变大 D.N变小,f变小
√
物块受力分析如图所示,有N′=G+F sin α,f=μN′。当力F与水平方向的夹角α变小时,地面对物块的支持力N′变小,动摩擦因数不变,物块受到的摩擦力f变小,根据牛顿第三定律可得,地面受到的压力N变小,D正确。
2.(多选)(人教必修第一册P79T3改编)某同学在实验室进行力学实验,如图所示,物体质量为m,用细绳OC悬在O点。现用同样材料的细绳AB绑住绳OC上的A点,用水平力F缓慢牵引A点,到图中虚线位置某绳刚好先断,相关实验结论符合事实的是
A.OA绳承受的力先增大后减小
B.若三根绳能承受的最大拉力相同,则OA绳先断
C.OA绳和AB绳的合力不变
D.AB绳受到的拉力逐渐增大
√
√
√
结点A下方AC绳始终受到向下大小为mg的力作用,还受到水平向右的拉力F作用及OA绳的拉力T作用,由三角形定则,可把三个力平移首尾依次相连,如图所示。当A点缓慢升高的过程中,拉力T不断逆时针转动,但始终与F及mg构成直角三角形,由图可知,OA绳承受的拉力T始终在增大,AB绳受到的拉力F逐渐增大。由于OA绳的拉力T作为三角形的斜边,拉力始终最大,会先达到能承受的最大拉力,若三根绳能承受的最大拉力相同,则OA绳会先断,A错误,B、D正确。OA绳和AB绳的合力始终等于物体的重力mg,故保持不变,C正确。
3.(多选)如图所示,轻质细杆AO、BO左端固定在竖直墙壁上,右端通过垂直于纸面的光滑轴连接于O点,AO水平,BO与竖直方向的夹角为θ。将质量为m的物体用轻绳悬挂在O点,物体静止时,若细杆AO对O点的拉力沿OA方向、大小为F1,细杆BO对O点的支持力沿BO方向、大小为F2,重力加速度为g,则
A.F1=mg tan θ B.F1=mg cos θ
C.F2= D.F2=
√
√
对O点受力分析,如图所示,根据共点力平衡可知F=T=mg,根据数
学知识可得F1=mg tan θ,F2= ,A、D正确,B、C错误。
4.用轻质细线把两个质量未知的小球悬挂起来,如图所示。对小球a持续施加一个水平向左的恒力,并对小球b持续施加一个水平向右的同样大小的恒力,最后达到平衡状态。下列选项中表示平衡状态的图可能是
√
将两球和两球之间的细线看成一个整体,对整体受力分析如图甲所示。根据平衡条件可知整体受到a球上方的细线的拉力F线的大小等于a、b的重力大小之和,方向沿竖直方向,故此细线必定沿竖直方向;对b球受力分析如图乙所示。根据平衡条件可知b球上方细线的拉力F线的大小等于b球重力与恒力F的合力,方向斜向左上方,故a、b球之间的线必定斜向左上方,故A正确。
返回
课 时 测 评
1.(多选)(2024·河南期末)某小城街道两旁的仿古路灯如图所示,灯笼悬挂在灯柱上,若风沿水平方向由左向右吹来,且风力缓慢增大,则
A.灯柱对灯笼的作用力逐渐减小
B.灯柱对灯笼的作用力逐渐增大
C.灯柱对灯笼的作用力与竖直方向的夹角逐渐增大
D.灯柱对灯笼的作用力与竖直方向的夹角逐渐减小
√
√
对灯笼受力分析,灯笼所受三力可构成力的矢量三角形,如图所示,可知风力F1越来越大时,灯柱对灯笼的作用力F2逐渐增大,灯柱对灯笼的作用力与竖直方向的夹角逐渐增大,A、D错误,B、C正确。
2.(2024·广东广州期末)如图所示,清洗楼房玻璃的工人常用一根悬绳将自己悬在空中,悬绳与竖直墙壁呈一定夹角,悬绳对工人的拉力大小为T,墙壁对工人的弹力大小为N,忽略一切摩擦。若缓慢减小悬绳的长度,下列说法正确的是
A.T减小,N减小
B.T减小,N增大
C.T与N的合力变大
D.T与N的合力不变
√
工人受到悬绳的拉力T、弹力N、重力G。在三个力的作用下平衡,则当缓慢减小悬绳的长度时,悬绳与墙壁的夹角逐渐增大,受力如图所示,即悬绳的拉力T从T1经T2逐渐变为T3,由此可知悬绳拉力T在逐渐变大,弹力N在逐渐增大,选项A、B错误;工人受力平衡,则T与N的合力与重力大小相等、方向相反,不会发生变化,选项C错误,D正确。
3.(多选)(2024·安徽师范大学附属中学期末)如图所示,用与竖直方向成θ角(θ<45°)的倾斜轻绳a和水平轻绳b共同固定一个小球,这时绳b的拉力为T1。现保持小球在原位置不动,使绳b在原竖直平面内沿逆时针方向转过θ角并固定,绳b的拉力变为T2;再转过θ角并固定,绳b的拉力变为T3,则
A.T1=T3>T2 B.T1<T2<T3
C.T1=T3<T2 D.随绳b转动,绳a的拉力减小
√
√
以小球为研究对象,小球受到重力、绳a的拉力T、绳b的拉力T1。根据平衡条件得知,T和T1的合力方向竖直向上,大小与重力相等,保持不变,作出绳b在三个不同位置时的拉力,如图所示,可得T1=T3>T2,且绳a的拉力不断减小,故A、D正确。
4.如图所示,固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔,质量为m的小球套在圆环上,一根细线的下端系着小球,上端穿过小孔用手拉住。现拉动细线,使小球沿圆环缓慢上移。在移动过程中手对线的拉力F和圆环对小球的弹力N的大小变化情况是
A.F减小,N不变 B.F不变,N减小
C.F不变,N增大 D.F增大,N减小
√
小球沿圆环缓慢上移可看作动态平衡,对小球进行受力分析,小球受重力G、拉力F′、弹力N三个力,其中F′=F。G与N的合力与F′等大反
向,如图所示,可知△OAB~△DCA,则 当A点上移时,圆
环半径R不变,AB长度减小,故F′=F减小,N不变,A正确。
5.(多选)倾角为α、质量为M的斜面体静止在水平桌面上,质量为m的木块静止在斜面体上。下列结论正确的是
A.木块受到的摩擦力大小是mg sin α
B.木块对斜面体的压力大小是mg sin α
C.桌面对斜面体的摩擦力大小是mgsin αcos α
D.桌面对斜面体的支持力大小是(M+m)g
√
√
以木块为研究对象,如图甲所示,有f=mg sin α,N=mg cos α,故A正确,B错误;以木块与斜面体所组成的整体为研究对象,如图乙所示,有f桌=0,N桌=(M+m)g,故C错误,D正确。
6.(2023·福建龙岩期末)如图所示,A、B两物体的质量分别为mA、mB,且mA>mB,整个系统处于静止状态,滑轮的质量和一切摩擦均不计,如果绳的一端由Q点缓慢地向左移到P点,整个系统重新静止后,绳的拉力F和绳与水平方向的夹角θ的变化情况是
A.F变大,θ角变大 B.F变小,θ角变小
C.F不变,θ角不变 D.F不变,θ角变小
√
重新静止后,绳的拉力F仍等于A物体的重力,B物体所受绳的拉力的合力与B物体的重力等大、反向,所以有2mAg sin θ=mBg,即sin θ= ,所以θ不变,C正确。
7.(多选)(2024·广东清远检测)如图所示,物体P静止于固定的斜面上,P的上表面水平。现把物体Q轻轻地叠放在P上,则(静大静摩擦力等于将动摩擦力)
A.P向下滑动 B.P静止不动
C.P所受的合外力增大 D.P与斜面间的静摩擦力增大
√
√
P在斜面上处于静止状态,设P的质量为M,斜面的倾角为θ,斜面与P之间的动摩擦因数为μ0,则有μ0Mgcos θ≥Mg sin θ,即μ≥tan θ;当加上一个质量为m的物体Q后,有μ0(M+m)g cos θ≥(M+m)g sin θ,因此P仍处于静止状态,选项A错误,B正确。由于P处于静止状态,合外力始终为零,选项C错误。由平衡条件知,P与斜面间的静摩擦力由Mg sin θ变为(M+m)g sin θ,选项D正确。
8.(2024·重庆市第十一中学期末)一横梁起重机移动货物时因出现故障而失去动力,工作人员在货物上作用一水平恒力,使货物和起重机一起缓慢向右移动,如图所示,已知起重机的质量为m1=1 kg,货物的质量为m2=3 kg,绳索与水平轨道间的夹角为θ=53°,绳索的质量不计(sin 53°=0.8,cos 53°=0.6),则水平横梁对起重机的阻力大小与横梁受到的压力大小的比值为
√
对货物和起重机分别受力分析,如图所示,对货物有T2sin θ=m2g,T2cos θ=F,对起重机有N=m1g+T1sin θ,f=T1cos θ,T1=T2,所以
有 选项A正确。
9.(10分)一盏电灯的重力为G,悬于天花板上A点,在电线O处系一细线OB,使电线OA与竖直方向的夹角为β=30°,如图所示。现保持β角不变,缓慢调整OB方向至OB线上拉力最小为止,此时OB与水平方向的夹角α等于多少?最小拉力是多少?
答案:30°
对电灯受力分析如图所示,据三力平衡特点可知OA、OB对O点的作用力TA、TB的合力T与G等大反向,即T=G
在△OTBT中,∠TOTB =90°-α
又∠OTTB=∠TOA=β,
故∠OTBT=180°-(90°-α)-β=90°+α-β
由正弦定理得=
联立解得TB=
因β不变,故当α=β=30°时,TB最小,且TB=G sin β= 。
10.(10分)如图甲所示,由两根短杆组成的一个自锁定起重吊钩,将它放入被吊的空罐内,使其张开一定的夹角压紧罐壁,内部结构如图乙所示,当钢绳向上提起时,两杆对罐壁越压越紧,摩擦力足够大时,就能将空罐提升起来,罐越重,短杆提供的压力越大,称为“自锁定吊钩”。若罐的质量为m,重力加速度为g,短杆与竖直方向的夹角θ=60°,求吊起该空罐时,每根短杆对罐壁的压力大小。(短杆的质量不计)
答案: mg
如图(a)所示,从整体来看,钢绳的拉力F=G,它可以分解为沿杆方向的两个大小相等的分力F′和F″,F′通过杆作用于罐壁,F′可分解为竖直向上的分力F1和垂直于罐壁的分力F2,如图(b)所示。由θ=60°及菱形知识得F′=F=G。
由图(b)可知F2=F′sin θ= 又F′垂直于罐壁的分力等于一根
短杆对罐壁的压力,所以每根短杆对罐壁的压力大小为 mg。
返回
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
