教科版高中物理必修第一册 第三章 相互作用6共点力作用下物体的平衡 课件(共79张PPT)
文档属性
| 名称 | 教科版高中物理必修第一册 第三章 相互作用6共点力作用下物体的平衡 课件(共79张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-28 00:00:00 | ||
图片预览









文档简介
(共79张PPT)
6.共点力作用下物体的平衡
第三章 相互作用
1.了解生活中的平衡现象,知道什么是平衡状态。
2.理解共点力的平衡条件。
3.学会用共点力的平衡条件分析平衡问题。
素养目标
知识点一 共点力作用下物体的平衡条件
自主学习
情境导入 如图所示,著名景点——黄山飞来石独自静止于悬崖之上。
(1)飞来石受哪些力作用?
提示:受重力和悬崖对它的作用力。
(2)这些力的大小、方向有何关系?它们的合力有何特点?
提示:重力方向竖直向下、悬崖对它的作用力方向竖直向上,二力等大、反向,合力为零。
教材梳理 (阅读教材P92—P94完成下列填空)
1.平衡状态:如果物体保持静止或__________运动状态,我们就说这个物体处于__________。
2.共点力平衡的条件:物体受到的__________。
匀速直线
平衡状态
合力为零
课堂探究
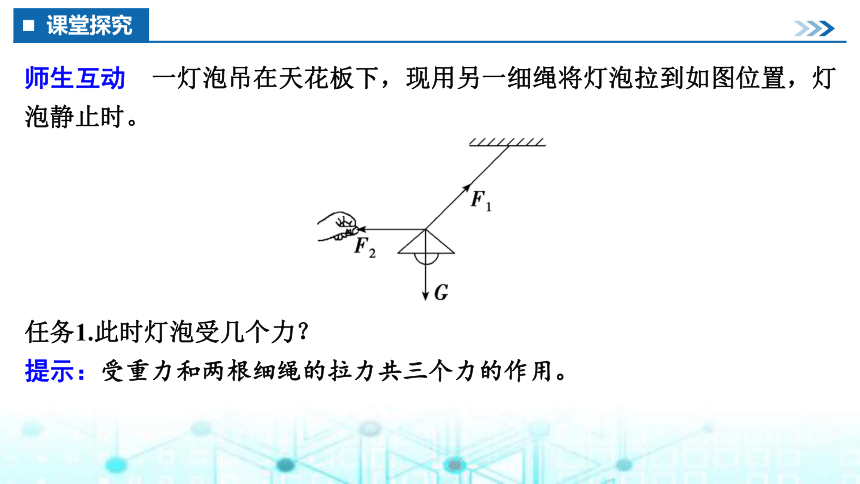
师生互动 一灯泡吊在天花板下,现用另一细绳将灯泡拉到如图位置,灯泡静止时。
任务1.此时灯泡受几个力?
提示:受重力和两根细绳的拉力共三个力的作用。
任务2.试根据二力平衡条件,推导说明:若一个物体受三个力作用而处于平衡状态,则其中一个力与另外两个力的合力满足怎样的关系?
提示:如图所示,灯泡受三个力的作用,将F1和F2合成,可以发现F1和F2的合力与重力G满足二力平衡,所以三个力平衡,则其中一个力与另外两个力的合力必定大小相等、方向相反。
任务3.上面探究的结论是否可以推广到多个力的平衡?
提示:可以。若物体受多个力的作用而处于平衡状态,则这些力中的某一个力一定与其余力的合力大小相等、方向相反。
物体受到共点力的作用,下列说法正确的是
A.在某一时刻速度等于零的物体一定处于平衡状态
B.相对于另一物体保持静止的物体一定处于平衡状态
C.物体所受合力为零时,一定处于平衡状态
D.物体运动时若速率不变,一定处于平衡状态
例1
√
处于平衡状态的物体,在运动形式上处于静止状态或匀速直线运动状态,从受力上来看,物体所受合力为零,C正确;某一时刻速度为零的物体,受力不一定为零,故不一定处于平衡状态,A错误;某物体相对于另一物体静止时,该物体不一定静止,如当另一物体做变速运动时,该物体也做相同的变速运动,此物体不处于平衡状态,故B错误;物体运动速度大小不变但方向变化时,所受合力不为零,故不处于平衡状态,D错误。
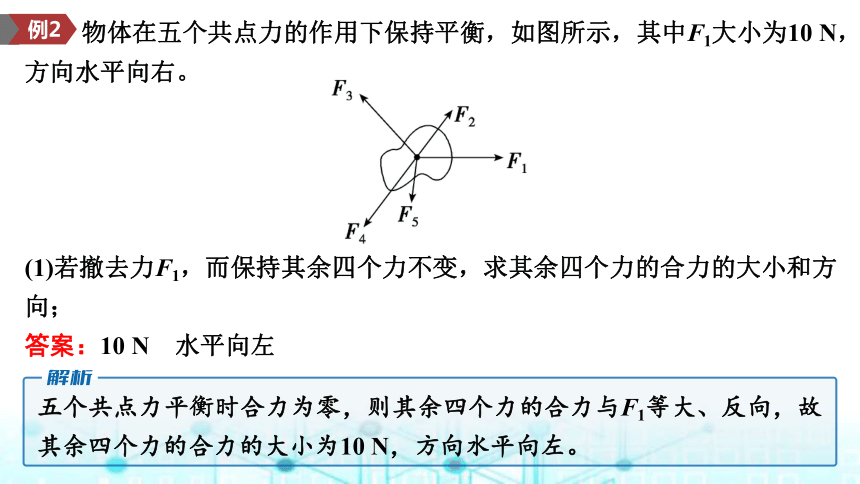
物体在五个共点力的作用下保持平衡,如图所示,其中F1大小为10 N,方向水平向右。
(1)若撤去力F1,而保持其余四个力不变,求其余四个力的合力的大小和方向;
答案:10 N 水平向左
例2
五个共点力平衡时合力为零,则其余四个力的合力与F1等大、反向,故其余四个力的合力的大小为10 N,方向水平向左。
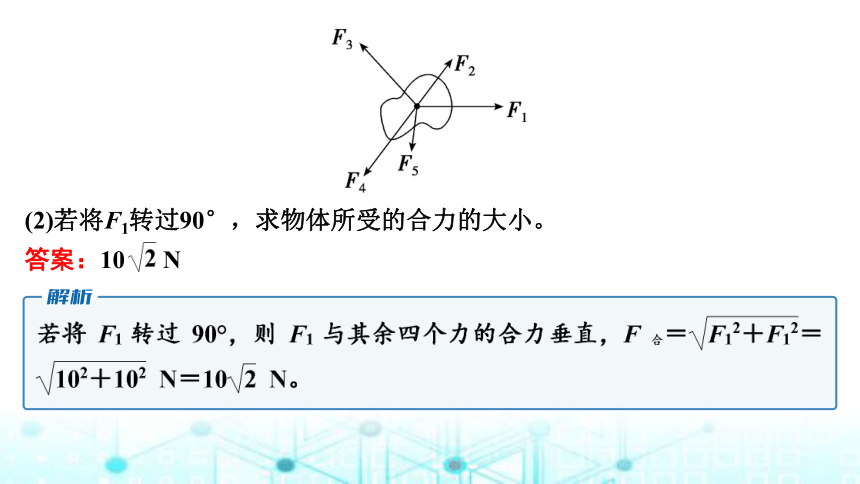
(2)若将F1转过90°,求物体所受的合力的大小。
答案:10 N
1.共点力平衡条件的理解
合外力等于0,即F合=0→正交分解表示 ,其中Fx合和Fy合分别表示物体在x轴和y轴上所受的合力。
2.共点力平衡条件的推论
(1)二力平衡:若物体在两个力作用下处于平衡状态,则这两个力一定等大、反向。
(2)三力平衡:若物体在三个共点力作用下处于平衡状态,则任意两个力的合力必定与第三个力等大、反向。
(3)多力平衡:若物体在n个共点力作用下处于平衡状态,则其中任意一个力必定与另外(n-1)个力的合力等大、反向。
针对练1.(2024·四川遂宁高一期末)关于平衡状态,下列说法正确的是
A.自由落体的物体不受空气阻力,所以处于平衡状态
B.运动的物体不可能处于平衡状态
C.物体处于平衡状态时所受合外力为0
D.当物体处于平衡状态时,一定不受外力作用
√
匀速直线运动状态和静止状态都是平衡状态,故运动的物体也可以处于平衡状态,故B错误;物体处于平衡状态时所受合外力为0,不是一定不受外力作用,故C正确,D错误;自由落体的物体只受重力作用,合外力不为0,不处于平衡状态,故A错误。
针对练2.一物体静止于水平桌面上,两者之间的最大静摩擦力为5 N,现将水平面内三个力同时作用于物体的同一点,三个力的大小分别为2 N、 2 N、3 N。下列判断正确的是
A.物体所受静摩擦力不可能为2 N B.物体所受静摩擦力不可能为4 N
C.物体可能仍保持静止 D.物体一定被拉动
√
2 N和2 N的力的合力范围为0≤F合≤4 N,3 N在此范围内,故当两个 2 N的力的合力为3 N,且与第三个力大小相等、方向相反时,三个力的合力为0,故2 N、2 N、3 N三个力的合力范围为0≤F合′≤7 N。2 N在三个力的合力范围内,故当三个力的合力为2 N时,物体所受静摩擦力为 2 N,故A错误;同理可知,B错误;当三个力的合力小于或等于最大静摩擦力5 N时,物体仍保持静止状态,故C正确,D错误。
返回
知识点二 解决共点力平衡问题的常用方法
合成法 物体在三个共点力作用下处于平衡时,将其中的任意两个力合成,其合力一定与第三个力平衡,从而把三力平衡问题转化为二力平衡问题
分解法 物体在三个共点力作用下处于平衡时,将其中任意一个力沿其他两个力的反方向分解,则每个方向上的一对力大小相等、方向相反,从而把三力平衡问题转化为两个方向上的二力平衡问题
正交分解法 物体在三个或三个以上的共点力作用下处于平衡时,将物体所受的各个力均向两个互相垂直的方向上分解,然后分别在这两个方向上列平衡方程,此时平衡条件可表示为Fx合=0,Fy合=0
用绳子将鸟笼挂在一根横梁上,如图所示。若鸟笼重19.6 N,请尝试利用合成法求解绳子OA和OB对结点O的拉力大小。
解题指导:以结点O为研究对象,它受到鸟笼上端绳子的拉力T,以及两段绳子OA和OB的拉力F1、F2。结点O在这三个共点力作用下处于平衡状态,其中,F1和F2的合力F与T大小相等、方向相反,T的大小与鸟笼所受重力大小相等。由此可通过平行四边形定则作图求解。
答案:17.0 N 9.8 N
例3
以结点O为研究对象,根据共点力的平衡条件,作受力分析如图所示。
F=T,且T=G
由三角函数关系得
F1=Fcos 30°=19.6× N≈17.0 N
F2 =Fsin 30°=19.6× N=9.8 N。
变式拓展1.请尝试利用分解法求解【例3】。
答案:17.0 N 9.8 N
以结点O为研究对象,根据共点力的平衡条件,作受力分析如图所示。
T=G,将拉力T向绳OA和OB的反向分解,由三角函数关系得
FA=Tcos 30°=19.6× N≈17.0 N
FB=Tsin 30°=19.6× N=9.8 N。
变式拓展2.请尝试利用正交分解法求解【例3】。
答案:17.0 N 9.8 N
如图所示,建立直角坐标系,将绳子OA和OB的拉力沿x轴、y轴方向正交分解。
T=G
由平衡条件得
水平方向F1cos 60°=F2cos 30°
竖直方向F1sin 60°+F2sin 30°=T
解得F1≈17.0 N,F2 =9.8 N。
变式拓展3.若【例3】中两绳能承受的最大拉力相同,均为100 N,重力加速度g为10 m/s2,持续增大悬挂物的质量,为了保证两段绳子不被拉断,求悬挂物的最大质量。
答案: kg
由题意知,绳子OA的拉力F1大于OB的拉力F2,为了保证两段绳子不被拉断,当绳子OA的拉力F1m=100 N时,悬挂物的质量达到最大
则有F1m=mgcos 30°,解得m= kg。
解答共点力平衡问题的一般步骤
1.选取研究对象。对于有相互作用的两个或两个以上的物体构成的系统,应明确所选研究对象是系统整体还是系统中的某一个物体(整体法或隔离法)。
2.对所选研究对象进行受力分析,并画出受力分析图。
3.对研究对象所受的力进行处理。对三力平衡问题,一般根据平衡条件画出力合成的平行四边形;对四力或四力以上的平衡问题,一般建立合适的直角坐标系,把不在坐标轴上的力分解到坐标轴上。
4.建立平衡方程并求解。
针对练1.如图所示,光滑半球形容器固定在水平面上,O为球心。一质量为m的小滑块,在水平恒力F的作用下静止于P点。设滑块所受支持力为N,OP与水平方向的夹角为θ,下列关系正确的是
A.F= B.F=mgtan θ
C.N= D.N=mg tan θ
√
法一:合成法
小滑块受力如图所示,由平衡条件知, A正确。
法二:正交分解法
将小滑决受的力沿水平、竖直方向分解,如图所示。在x轴与y轴方向由
平衡条件得mg=N sin θ,F=N cos θ,联立解得 A正确。
针对练2.“风力仪”可直接测量风力的大小,其原理如图所示。仪器中一根轻质金属丝悬挂着一个金属球。无风时,金属丝竖直下垂;当受到沿水平方向吹来的风时,金属丝偏离竖直方向一个角度。风力越大,偏角越大。通过传感器,就可以根据偏角的大小指示出风力大小。那么风力大小F跟金属球的质量m、偏角θ之间有什么样的关系呢?(重力加速度为g)
答案:F=mg tan θ
选取金属球为研究对象,它受到三个力的作用,如图甲所示。金属球处于平衡状态,这三个力的合力为零。可用以下三种方法求解。
法一:合成法
如图乙所示,风力F和拉力T的合力与金属球所受的重力等大反向,由平行四边形定则可得F=mg tan θ。
法二:分解法
重力有两个作用效果:使金属球抵抗风的吹力和使金属丝拉紧,可以将金属球所受的重力沿水平方向和金属丝的方向进行分解,如图丙所示,由几何关系可得F=F′=mg tan θ。
法三:正交分解法
以金属球为坐标原点,取水平方向为x轴,竖直方向为y
轴,建立坐标系,如图丁所示。由水平方向的合力Fx合
和竖直方向的合力Fy合分别等于零得
Fx合=T sin θ-F=0
Fy合=T cos θ-mg=0
解得F=mg tan θ。
返回
知识点三 “活结”与“死结”、“动杆”
与“定杆”模型
1.“活结”与“死结”模型
(1)“活结”:一般是由轻绳跨过光滑滑轮或者绳上挂一光滑挂钩而形成的。绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线。
(2)“死结”:两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。
2.“动杆”与“定杆”模型
(1)“动杆”:轻杆用转轴或铰链连接,当杆处于平衡状态时,杆所受到的弹力方向一定沿着杆,否则会引起杆的转动。如图甲所示,若C为转轴,则轻杆在缓慢转动中,弹力方向始终沿杆的方向。
(2)“定秆”:若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向。如图乙所示,水平横梁的一端A插在墙壁内,另一端装有一个小滑轮B,一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂质量为m的重物。滑轮对绳子的作用力应为图丙中两段绳中拉力F1和F2的合力F的反作用力,即定杆弹力的方向可以不沿杆的方向。
角度1 “活结”与“死结”模型
(2024·云南省保山市期末)如图,悬挂甲物体的细线拴牢在一不可伸长的轻质细绳上O点处,绳的一端固定在墙上,另一端通过光滑定滑轮与物体乙相连。甲、乙两物体质量相等,系统平衡时,O点两侧绳与竖直方向的夹角分别为α和β。若α=50°,则β等于
A.70° B.65°
C.50° D.40°
例4
√
甲物体是拴牢在O点,且甲、乙两物体的质量相等,则与甲、乙相连的绳的拉力大小相等,O点处于平衡状态,其受力情况如图所示,根据几何关系有180°=2β+α,解得β=65°,B正确。
角度2 “动杆”与“定杆”模型
如图所示,在水平天花板的A点处固定一根轻杆a,杆与天花板保持垂直。杆的下端有一个轻滑轮O。另一根细线上端固定在该天花板的B点处,细线跨过滑轮O,下端系一个重为G的物体,BO段细线与天花板的夹角为θ=30°。系统保持静止,不计一切摩擦。下列说法中正确的是
A.细线BO对天花板的拉力大小是3G
B.a杆对滑轮的作用力大小是1.8G
C.a杆和细线对滑轮的作用力的合力大小是2G
D.a杆对滑轮的作用力大小是G
例5
√
细线上的拉力处处相等,因此细线BO对天花板的拉力大小是G,故A错误;两段细线上拉力大小均为G,合力为2Gcos 60°=G,大小等于a杆对滑轮的作用力,故B错误,D正确;a杆和细线对滑轮的作用力的合力大小是0,故C错误。
针对练1.(多选)如图所示,一条细线一端与地板上的物块B相连,另一端绕过轻质光滑滑轮与小球A相连。滑轮用另一条细线悬挂在天花板上的O1点,细线OO1与竖直方向夹角为α=30°,OA与OB的夹角为θ,系统处于静止状态。已知小球A的重力为10 N,则
A.细线OA的拉力为10 N
B.OO1线上的拉力大小为20 N
C.地板对B的摩擦力大小为5 N
D.细线OA与OB间的夹角θ=60°
√
√
对小球A受力分析,其受重力和拉力,根据平衡条件有
TA=mg=10 N,故A正确;对滑轮分析,受三个拉力作
用,如图所示,由分析可知θ=2α=60°,由平衡条件
知F=2TA cos α=10 N,故B错误,D正确;对物块B
受力分析,其受重力、支持力、拉力和静摩擦力,根据
平衡条件,水平方向有TB sin θ=f,又因为TA=TB,解
得f=5 N,故C错误。
针对练2.如图甲所示,细绳AD跨过固定的水平轻杆BC右端的轻质光滑定滑轮悬挂一质量为M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙壁上,另一端G通过细绳EG拉住,EG与水平方向的夹角为30°,在轻杆的G点用细绳GF悬挂一质量为M2的物体(都处于静止状态),求:
(1)细绳AC段的张力TAC与细绳EG的张力TEG之比;
答案:
题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡条件,首先判断与物体相连的细绳的拉力大小等于物体所受的重力;分别取C点和G点为研究对象,进行受力分析如图1和2所示,根据平衡规律求解。
图1中细绳AD跨过轻质光滑定滑轮悬挂质量为M1的物体,物体处于平衡状态,细绳AC段的拉力TAC=TCD=M1g
图2中由TEGsin 30°=M2g,得TEG=2M2g
所以 。
(2)轻杆BC对C端的支持力;
答案:M1g,方向与水平方向成30°指向右上方
题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡条件,首先判断与物体相连的细绳的拉力大小等于物体所受的重力;分别取C点和G点为研究对象,进行受力分析如图1和2所示,根据平衡规律求解。
图1中,TAC、NC、M1g三个力之间的夹角都为120°,根据平衡规律有NC=TAC=M1g,NC的方向与水平方向成30°指向右上方。
(3)轻杆HG对G端的支持力。
答案: M2g,方向水平向右
题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡条件,首先判断与物体相连的细绳的拉力大小等于物体所受的重力;分别取C点和G点为研究对象,进行受力分析如图1和2所示,根据平衡规律求解。
图2中,根据平衡规律有 方向水平向右。
返回
随堂演练
1.(人教必修第一册P79T1改编)如图所示,某物体在4个共点力作用下处于静止状态,若F1的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此物体受到的合力大小变为
A.F1 B.2F1
C. F1 D. F1
√
原来物体静止,四个共点力的合力为零,则F2、F3、F4三个力的合力F′与F1大小相等、方向相反,将F1的方向沿逆时针转过60°后,F′与F1的夹角为120°,则此物体受到的合力大小变为F1,A正确。
2.如图所示,高空走钢丝的表演中,若表演者走到钢丝中点时,使原来水平的钢丝下垂与水平面成θ角,此时钢丝上的弹力应是表演者和平衡杆的总重力的
√
以表演者和平衡杆为研究对象,分析其受力情况,如图所示,根据平衡条件,可知两钢丝上弹力的合力与总重力等大反向,则有2F sin θ=mg,
解得F= ,故钢丝上的弹力应是表演者和平衡杆总重力的 ,
C正确。
3.(多选)(人教必修第一册P79T2改编)在光滑墙壁上用网兜把足球挂在A点,足球与墙壁的接触点为B。足球的质量为m,悬绳与墙壁的夹角为α,网兜的质量不计,则
A.悬绳对球的拉力为G sin α
B.悬绳对球的拉力为
C.墙壁对球的支持力为
D.墙壁对球的支持力为G tan α
√
√
足球受到三个力的作用,这三个力构成矢量三角形如图所示,由图可知悬绳对球的拉力T= ,墙壁对球的支持力N=G tan α,故B、D正确。
4.(粤教必修第一册P90例题2改编)一种测定风力的仪器如图所示,它的细长金属丝一端固定于悬点O,另一端悬挂一个质量为m的金属球。无风时,金属丝自然下垂,当受到沿水平方向吹来的风时,金属丝偏离竖直方向的角度为θ。风力F与θ、m之间的关系式正确的是
A.F=mg sin θ
B.F=mg cos θ
C.F=mg tan θ
D.F=
√
对金属球受力分析,如图所示,金属球受到重力、拉力和风力共3个力作用,根据共点力平衡条件可知,拉力和风力的合力与重力平衡,由几何关系得到F=mg tan θ,C正确。
返回
课 时 测 评
1.若某一物体受共点力作用处于平衡状态,则该物体
A.一定是静止的
B.一定做匀速直线运动
C.所受各共点力的合力可能不为零
D.所受各共点力的合力为零
√
物体处于平衡状态时,物体可能静止或做匀速直线运动,选项A、B错误;此时所受各共点力的合力一定为零,选项C错误,D正确。
2.(2024·浙江杭州余杭二中测试)树懒是一种懒得出奇的哺乳动物,什么事都懒得做,甚至懒得去吃,懒得去玩耍,能耐饥一个月以上,非得活动不可时,动作也是懒洋洋的,极其迟缓。树懒静止倒挂在树干上时,树干给树懒的力的方向为
A.垂直于树干向上
B.沿树干向上
C.竖直向上
D.树干形变复杂,无法判断力的方向
√
树懒静止倒挂在树干上,则所受的重力与树干对它的作用力平衡,可知树干给树懒的力的方向为竖直向上,故选C。
3.(2022·重庆高考)如图所示,吸附在竖直玻璃上质量为m的擦窗工具,在竖直平面内受重力、拉力和摩擦力(图中未画出摩擦力)的共同作用做匀速直线运动。若拉力大小与重力大小相等,方向水平向右,重力加速度为g,则擦窗工具所受摩擦力
A.大小等于mg B.大小等于 mg
C.方向竖直向上 D.方向水平向左
√
擦窗工具做匀速直线运动,所受合力为0,则摩擦力大小等于重力和拉力的合力,拉力大小等于重力,则f= mg,方向斜向左上方与水平方向夹角为45°,故B正确。
4.在如图所示的四幅图中,AB、BC均为轻质杆,各图中杆的A、C端都通过铰链与墙连接,两杆都在B处由铰链相连接。下列说法正确的是
A.图中的AB杆可以用与之等长的轻绳代替的有甲、乙
B.图中的AB杆可以用与之等长的轻绳代替的有甲、丙、丁
C.图中的BC杆可以用与之等长的轻绳代替的有乙、丙
D.图中的BC杆可以用与之等长的轻绳代替的有乙、丁
√
轻绳只能产生拉力,而杆可产生拉力也可产生推力,故能用绳代替杆的情况是杆中的力为拉力。题图甲、丙、丁中AB杆产生的是拉力,题图丙中BC杆产生的是拉力,B正确。
5.如图所示,在水平天花板上用绳AC、BC和CD吊起一个物体,使其处于静止状态,结点为C,绳子的长度分别为AC=4 dm,BC=3 dm,悬点A、B间距为5 dm。则AC绳、BC绳、CD绳上的拉力大小之比为
A.20∶15∶12 B.4∶3∶5
C.3∶4∶5 D.因CD绳长未知,故无法确定
√
对三条绳的结点C进行受力分析,如图所示,由共点力平衡的条件知,AC、BC绳上拉力的合力与CD绳上的拉力等大反向。由几何关系知,AC绳、BC绳、CD绳上的拉力大小之比为3∶4∶5,所以C正确。
6.(多选)一个大人拉着载有两个小孩的小车(其拉杆可自由转动)沿水平地面匀速直线前进,则对小孩和车下列说法正确的是
A.拉力的水平分力等于小孩和车所受的合力
B.拉力与摩擦力的合力大小等于重力大小
C.拉力与摩擦力的合力方向竖直向上
D.小孩和车所受的合力为零
√
小孩和车做匀速直线运动,故小孩和车所受的合力为零。小孩和车整体受重力、支持力、拉力和摩擦力,根据共点力平衡条件,拉力的水平分力等于小孩和车所受的摩擦力,故A错误,D正确;拉力、摩擦力的合力与重力、支持力的合力平衡,重力、支持力的合力竖直,故拉力与摩擦力的合力方向竖直向上,故B错误,C正确。
√
7.放假了,小明斜拉着拉杆箱离开校园。如图所示,小明的拉力大小为F,方向沿拉杆斜向上,与水平地面夹角为θ。与拉杆箱竖直静止在水平地面且不受拉力相比,此时水平地面对拉杆箱的支持力
A.减少了F sin θ B.增大了F sin θ
C.减少了F cos θ D.增大了F cos θ
√
以箱子为研究对象,受到重力、支持力、拉力和摩擦力,如图所示,没有拉力时,支持力等于重力mg;有拉力F时,支持力为N=mg-F sin θ,所以支持力减少了F sin θ,故A正确。
8.如图所示的几种情况中,不计绳、弹簧测力计、各滑轮的质量,不计一切摩擦,物体质量都为m,且均处于静止状态,有关角度图中已标出。弹簧测力计的示数分别为FA、FB、FC、FD,则
A.FB>FD>FA>FC B.FD>FC>FB>FA
C.FD>FB>FA>FC D.FC>FD>FB>FA
√
9.(多选)将沙桶P用细绳系在C点,如图所示,在两沙桶中装上一定质量的沙子,沙桶(含沙子)P、Q的总质量分别为m1、m2,系统平衡时,∠ACB=90°、∠CAB=60°,忽略滑轮的大小以及摩擦。则下列说法正确的是
A.m1∶m2=1∶1
B.m1∶m2=2∶1
C.若在两桶内增加相同质量的沙子,C点的位置上升
D.若在两桶内增加相同质量的沙子,C点的位置保持不变
√
√
以结点C为研究对象,受力分析如图所示,其中F=m1g、FB=m2g,由力的平衡条件可知FA=F cos 30°=m1g cos 30°,由几何关系可知FA=
,联立解得m1∶m2=2∶1,选项A错误,B正确;由以上分析可知,若在两桶内增加相同质量的沙子,则两沙桶(含沙子)质量的比值会小于2,则Q桶向下移动,C点的位置上升,选项C正确,D错误。
10.如图所示,两个质量为m1的小球套在竖直放置的光滑支架上,支架的夹角为120°,用轻绳将两球与质量为m2的小球连接,轻绳与支架构成一个菱形,则m1∶m2为
A.1∶1 B.1∶2
C.1∶ D. ∶2
√
将小球m2受到的重力按作用效果根据平行四边形定则进行分解,如图所示,由几何知识得T=m2g;对m1受力分析,由平衡条件,在沿支架的方向上有m1g sin 30°=T sin 30°,可得T=m1g,则m1∶m2=1∶1,故A正确。
11.(10分)(2024·山东德州高一月考)如图所示,在倾角θ=37°的固定斜面上,用一水平力F推一质量m=10 kg的物体,欲使物体沿斜面做匀速直线运动,已知物体与斜面间的动摩擦因数μ=0.2,求F的大小(结果保留到个位,sin 37°=0.6,cos 37°=0.8,g取10 m/s2)。
答案:112 N或48 N
若物体沿斜面向上做匀速直线运动,对物体受力析如图甲所示
根据平衡条件得
F cos θ=f+mg sin θ
N=mg cos θ+F sin θ
又f=μN
解得F≈112 N;
若物体沿斜面向下做匀速直线运动,对物体受力析如图乙所示
根据平衡条件得
F cos θ+f′=mg sin θ
N′= F sin θ+mg cos θ
又f′=μN′
解得F≈48 N。
12.(10分)如图所示,A球和B球用轻绳相连,静止在光滑的圆柱面上,若A球的质量为m,则B球的质量为多少?(A、B两球可视为质点,sin 37°=0.6,sin 53°=0.8)
答案: m
解析:球很小,可认为绳拉球的方向在大圆的切线方向上。分别对A、B进行受力分析如图
对A:mgsin 37°=FA
对B:Mgsin 53°=FB
又FA=FB
联立解得M= m。
返回
6.共点力作用下物体的平衡
第三章 相互作用
1.了解生活中的平衡现象,知道什么是平衡状态。
2.理解共点力的平衡条件。
3.学会用共点力的平衡条件分析平衡问题。
素养目标
知识点一 共点力作用下物体的平衡条件
自主学习
情境导入 如图所示,著名景点——黄山飞来石独自静止于悬崖之上。
(1)飞来石受哪些力作用?
提示:受重力和悬崖对它的作用力。
(2)这些力的大小、方向有何关系?它们的合力有何特点?
提示:重力方向竖直向下、悬崖对它的作用力方向竖直向上,二力等大、反向,合力为零。
教材梳理 (阅读教材P92—P94完成下列填空)
1.平衡状态:如果物体保持静止或__________运动状态,我们就说这个物体处于__________。
2.共点力平衡的条件:物体受到的__________。
匀速直线
平衡状态
合力为零
课堂探究
师生互动 一灯泡吊在天花板下,现用另一细绳将灯泡拉到如图位置,灯泡静止时。
任务1.此时灯泡受几个力?
提示:受重力和两根细绳的拉力共三个力的作用。
任务2.试根据二力平衡条件,推导说明:若一个物体受三个力作用而处于平衡状态,则其中一个力与另外两个力的合力满足怎样的关系?
提示:如图所示,灯泡受三个力的作用,将F1和F2合成,可以发现F1和F2的合力与重力G满足二力平衡,所以三个力平衡,则其中一个力与另外两个力的合力必定大小相等、方向相反。
任务3.上面探究的结论是否可以推广到多个力的平衡?
提示:可以。若物体受多个力的作用而处于平衡状态,则这些力中的某一个力一定与其余力的合力大小相等、方向相反。
物体受到共点力的作用,下列说法正确的是
A.在某一时刻速度等于零的物体一定处于平衡状态
B.相对于另一物体保持静止的物体一定处于平衡状态
C.物体所受合力为零时,一定处于平衡状态
D.物体运动时若速率不变,一定处于平衡状态
例1
√
处于平衡状态的物体,在运动形式上处于静止状态或匀速直线运动状态,从受力上来看,物体所受合力为零,C正确;某一时刻速度为零的物体,受力不一定为零,故不一定处于平衡状态,A错误;某物体相对于另一物体静止时,该物体不一定静止,如当另一物体做变速运动时,该物体也做相同的变速运动,此物体不处于平衡状态,故B错误;物体运动速度大小不变但方向变化时,所受合力不为零,故不处于平衡状态,D错误。
物体在五个共点力的作用下保持平衡,如图所示,其中F1大小为10 N,方向水平向右。
(1)若撤去力F1,而保持其余四个力不变,求其余四个力的合力的大小和方向;
答案:10 N 水平向左
例2
五个共点力平衡时合力为零,则其余四个力的合力与F1等大、反向,故其余四个力的合力的大小为10 N,方向水平向左。
(2)若将F1转过90°,求物体所受的合力的大小。
答案:10 N
1.共点力平衡条件的理解
合外力等于0,即F合=0→正交分解表示 ,其中Fx合和Fy合分别表示物体在x轴和y轴上所受的合力。
2.共点力平衡条件的推论
(1)二力平衡:若物体在两个力作用下处于平衡状态,则这两个力一定等大、反向。
(2)三力平衡:若物体在三个共点力作用下处于平衡状态,则任意两个力的合力必定与第三个力等大、反向。
(3)多力平衡:若物体在n个共点力作用下处于平衡状态,则其中任意一个力必定与另外(n-1)个力的合力等大、反向。
针对练1.(2024·四川遂宁高一期末)关于平衡状态,下列说法正确的是
A.自由落体的物体不受空气阻力,所以处于平衡状态
B.运动的物体不可能处于平衡状态
C.物体处于平衡状态时所受合外力为0
D.当物体处于平衡状态时,一定不受外力作用
√
匀速直线运动状态和静止状态都是平衡状态,故运动的物体也可以处于平衡状态,故B错误;物体处于平衡状态时所受合外力为0,不是一定不受外力作用,故C正确,D错误;自由落体的物体只受重力作用,合外力不为0,不处于平衡状态,故A错误。
针对练2.一物体静止于水平桌面上,两者之间的最大静摩擦力为5 N,现将水平面内三个力同时作用于物体的同一点,三个力的大小分别为2 N、 2 N、3 N。下列判断正确的是
A.物体所受静摩擦力不可能为2 N B.物体所受静摩擦力不可能为4 N
C.物体可能仍保持静止 D.物体一定被拉动
√
2 N和2 N的力的合力范围为0≤F合≤4 N,3 N在此范围内,故当两个 2 N的力的合力为3 N,且与第三个力大小相等、方向相反时,三个力的合力为0,故2 N、2 N、3 N三个力的合力范围为0≤F合′≤7 N。2 N在三个力的合力范围内,故当三个力的合力为2 N时,物体所受静摩擦力为 2 N,故A错误;同理可知,B错误;当三个力的合力小于或等于最大静摩擦力5 N时,物体仍保持静止状态,故C正确,D错误。
返回
知识点二 解决共点力平衡问题的常用方法
合成法 物体在三个共点力作用下处于平衡时,将其中的任意两个力合成,其合力一定与第三个力平衡,从而把三力平衡问题转化为二力平衡问题
分解法 物体在三个共点力作用下处于平衡时,将其中任意一个力沿其他两个力的反方向分解,则每个方向上的一对力大小相等、方向相反,从而把三力平衡问题转化为两个方向上的二力平衡问题
正交分解法 物体在三个或三个以上的共点力作用下处于平衡时,将物体所受的各个力均向两个互相垂直的方向上分解,然后分别在这两个方向上列平衡方程,此时平衡条件可表示为Fx合=0,Fy合=0
用绳子将鸟笼挂在一根横梁上,如图所示。若鸟笼重19.6 N,请尝试利用合成法求解绳子OA和OB对结点O的拉力大小。
解题指导:以结点O为研究对象,它受到鸟笼上端绳子的拉力T,以及两段绳子OA和OB的拉力F1、F2。结点O在这三个共点力作用下处于平衡状态,其中,F1和F2的合力F与T大小相等、方向相反,T的大小与鸟笼所受重力大小相等。由此可通过平行四边形定则作图求解。
答案:17.0 N 9.8 N
例3
以结点O为研究对象,根据共点力的平衡条件,作受力分析如图所示。
F=T,且T=G
由三角函数关系得
F1=Fcos 30°=19.6× N≈17.0 N
F2 =Fsin 30°=19.6× N=9.8 N。
变式拓展1.请尝试利用分解法求解【例3】。
答案:17.0 N 9.8 N
以结点O为研究对象,根据共点力的平衡条件,作受力分析如图所示。
T=G,将拉力T向绳OA和OB的反向分解,由三角函数关系得
FA=Tcos 30°=19.6× N≈17.0 N
FB=Tsin 30°=19.6× N=9.8 N。
变式拓展2.请尝试利用正交分解法求解【例3】。
答案:17.0 N 9.8 N
如图所示,建立直角坐标系,将绳子OA和OB的拉力沿x轴、y轴方向正交分解。
T=G
由平衡条件得
水平方向F1cos 60°=F2cos 30°
竖直方向F1sin 60°+F2sin 30°=T
解得F1≈17.0 N,F2 =9.8 N。
变式拓展3.若【例3】中两绳能承受的最大拉力相同,均为100 N,重力加速度g为10 m/s2,持续增大悬挂物的质量,为了保证两段绳子不被拉断,求悬挂物的最大质量。
答案: kg
由题意知,绳子OA的拉力F1大于OB的拉力F2,为了保证两段绳子不被拉断,当绳子OA的拉力F1m=100 N时,悬挂物的质量达到最大
则有F1m=mgcos 30°,解得m= kg。
解答共点力平衡问题的一般步骤
1.选取研究对象。对于有相互作用的两个或两个以上的物体构成的系统,应明确所选研究对象是系统整体还是系统中的某一个物体(整体法或隔离法)。
2.对所选研究对象进行受力分析,并画出受力分析图。
3.对研究对象所受的力进行处理。对三力平衡问题,一般根据平衡条件画出力合成的平行四边形;对四力或四力以上的平衡问题,一般建立合适的直角坐标系,把不在坐标轴上的力分解到坐标轴上。
4.建立平衡方程并求解。
针对练1.如图所示,光滑半球形容器固定在水平面上,O为球心。一质量为m的小滑块,在水平恒力F的作用下静止于P点。设滑块所受支持力为N,OP与水平方向的夹角为θ,下列关系正确的是
A.F= B.F=mgtan θ
C.N= D.N=mg tan θ
√
法一:合成法
小滑块受力如图所示,由平衡条件知, A正确。
法二:正交分解法
将小滑决受的力沿水平、竖直方向分解,如图所示。在x轴与y轴方向由
平衡条件得mg=N sin θ,F=N cos θ,联立解得 A正确。
针对练2.“风力仪”可直接测量风力的大小,其原理如图所示。仪器中一根轻质金属丝悬挂着一个金属球。无风时,金属丝竖直下垂;当受到沿水平方向吹来的风时,金属丝偏离竖直方向一个角度。风力越大,偏角越大。通过传感器,就可以根据偏角的大小指示出风力大小。那么风力大小F跟金属球的质量m、偏角θ之间有什么样的关系呢?(重力加速度为g)
答案:F=mg tan θ
选取金属球为研究对象,它受到三个力的作用,如图甲所示。金属球处于平衡状态,这三个力的合力为零。可用以下三种方法求解。
法一:合成法
如图乙所示,风力F和拉力T的合力与金属球所受的重力等大反向,由平行四边形定则可得F=mg tan θ。
法二:分解法
重力有两个作用效果:使金属球抵抗风的吹力和使金属丝拉紧,可以将金属球所受的重力沿水平方向和金属丝的方向进行分解,如图丙所示,由几何关系可得F=F′=mg tan θ。
法三:正交分解法
以金属球为坐标原点,取水平方向为x轴,竖直方向为y
轴,建立坐标系,如图丁所示。由水平方向的合力Fx合
和竖直方向的合力Fy合分别等于零得
Fx合=T sin θ-F=0
Fy合=T cos θ-mg=0
解得F=mg tan θ。
返回
知识点三 “活结”与“死结”、“动杆”
与“定杆”模型
1.“活结”与“死结”模型
(1)“活结”:一般是由轻绳跨过光滑滑轮或者绳上挂一光滑挂钩而形成的。绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线。
(2)“死结”:两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。
2.“动杆”与“定杆”模型
(1)“动杆”:轻杆用转轴或铰链连接,当杆处于平衡状态时,杆所受到的弹力方向一定沿着杆,否则会引起杆的转动。如图甲所示,若C为转轴,则轻杆在缓慢转动中,弹力方向始终沿杆的方向。
(2)“定秆”:若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向。如图乙所示,水平横梁的一端A插在墙壁内,另一端装有一个小滑轮B,一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂质量为m的重物。滑轮对绳子的作用力应为图丙中两段绳中拉力F1和F2的合力F的反作用力,即定杆弹力的方向可以不沿杆的方向。
角度1 “活结”与“死结”模型
(2024·云南省保山市期末)如图,悬挂甲物体的细线拴牢在一不可伸长的轻质细绳上O点处,绳的一端固定在墙上,另一端通过光滑定滑轮与物体乙相连。甲、乙两物体质量相等,系统平衡时,O点两侧绳与竖直方向的夹角分别为α和β。若α=50°,则β等于
A.70° B.65°
C.50° D.40°
例4
√
甲物体是拴牢在O点,且甲、乙两物体的质量相等,则与甲、乙相连的绳的拉力大小相等,O点处于平衡状态,其受力情况如图所示,根据几何关系有180°=2β+α,解得β=65°,B正确。
角度2 “动杆”与“定杆”模型
如图所示,在水平天花板的A点处固定一根轻杆a,杆与天花板保持垂直。杆的下端有一个轻滑轮O。另一根细线上端固定在该天花板的B点处,细线跨过滑轮O,下端系一个重为G的物体,BO段细线与天花板的夹角为θ=30°。系统保持静止,不计一切摩擦。下列说法中正确的是
A.细线BO对天花板的拉力大小是3G
B.a杆对滑轮的作用力大小是1.8G
C.a杆和细线对滑轮的作用力的合力大小是2G
D.a杆对滑轮的作用力大小是G
例5
√
细线上的拉力处处相等,因此细线BO对天花板的拉力大小是G,故A错误;两段细线上拉力大小均为G,合力为2Gcos 60°=G,大小等于a杆对滑轮的作用力,故B错误,D正确;a杆和细线对滑轮的作用力的合力大小是0,故C错误。
针对练1.(多选)如图所示,一条细线一端与地板上的物块B相连,另一端绕过轻质光滑滑轮与小球A相连。滑轮用另一条细线悬挂在天花板上的O1点,细线OO1与竖直方向夹角为α=30°,OA与OB的夹角为θ,系统处于静止状态。已知小球A的重力为10 N,则
A.细线OA的拉力为10 N
B.OO1线上的拉力大小为20 N
C.地板对B的摩擦力大小为5 N
D.细线OA与OB间的夹角θ=60°
√
√
对小球A受力分析,其受重力和拉力,根据平衡条件有
TA=mg=10 N,故A正确;对滑轮分析,受三个拉力作
用,如图所示,由分析可知θ=2α=60°,由平衡条件
知F=2TA cos α=10 N,故B错误,D正确;对物块B
受力分析,其受重力、支持力、拉力和静摩擦力,根据
平衡条件,水平方向有TB sin θ=f,又因为TA=TB,解
得f=5 N,故C错误。
针对练2.如图甲所示,细绳AD跨过固定的水平轻杆BC右端的轻质光滑定滑轮悬挂一质量为M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙壁上,另一端G通过细绳EG拉住,EG与水平方向的夹角为30°,在轻杆的G点用细绳GF悬挂一质量为M2的物体(都处于静止状态),求:
(1)细绳AC段的张力TAC与细绳EG的张力TEG之比;
答案:
题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡条件,首先判断与物体相连的细绳的拉力大小等于物体所受的重力;分别取C点和G点为研究对象,进行受力分析如图1和2所示,根据平衡规律求解。
图1中细绳AD跨过轻质光滑定滑轮悬挂质量为M1的物体,物体处于平衡状态,细绳AC段的拉力TAC=TCD=M1g
图2中由TEGsin 30°=M2g,得TEG=2M2g
所以 。
(2)轻杆BC对C端的支持力;
答案:M1g,方向与水平方向成30°指向右上方
题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡条件,首先判断与物体相连的细绳的拉力大小等于物体所受的重力;分别取C点和G点为研究对象,进行受力分析如图1和2所示,根据平衡规律求解。
图1中,TAC、NC、M1g三个力之间的夹角都为120°,根据平衡规律有NC=TAC=M1g,NC的方向与水平方向成30°指向右上方。
(3)轻杆HG对G端的支持力。
答案: M2g,方向水平向右
题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡条件,首先判断与物体相连的细绳的拉力大小等于物体所受的重力;分别取C点和G点为研究对象,进行受力分析如图1和2所示,根据平衡规律求解。
图2中,根据平衡规律有 方向水平向右。
返回
随堂演练
1.(人教必修第一册P79T1改编)如图所示,某物体在4个共点力作用下处于静止状态,若F1的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此物体受到的合力大小变为
A.F1 B.2F1
C. F1 D. F1
√
原来物体静止,四个共点力的合力为零,则F2、F3、F4三个力的合力F′与F1大小相等、方向相反,将F1的方向沿逆时针转过60°后,F′与F1的夹角为120°,则此物体受到的合力大小变为F1,A正确。
2.如图所示,高空走钢丝的表演中,若表演者走到钢丝中点时,使原来水平的钢丝下垂与水平面成θ角,此时钢丝上的弹力应是表演者和平衡杆的总重力的
√
以表演者和平衡杆为研究对象,分析其受力情况,如图所示,根据平衡条件,可知两钢丝上弹力的合力与总重力等大反向,则有2F sin θ=mg,
解得F= ,故钢丝上的弹力应是表演者和平衡杆总重力的 ,
C正确。
3.(多选)(人教必修第一册P79T2改编)在光滑墙壁上用网兜把足球挂在A点,足球与墙壁的接触点为B。足球的质量为m,悬绳与墙壁的夹角为α,网兜的质量不计,则
A.悬绳对球的拉力为G sin α
B.悬绳对球的拉力为
C.墙壁对球的支持力为
D.墙壁对球的支持力为G tan α
√
√
足球受到三个力的作用,这三个力构成矢量三角形如图所示,由图可知悬绳对球的拉力T= ,墙壁对球的支持力N=G tan α,故B、D正确。
4.(粤教必修第一册P90例题2改编)一种测定风力的仪器如图所示,它的细长金属丝一端固定于悬点O,另一端悬挂一个质量为m的金属球。无风时,金属丝自然下垂,当受到沿水平方向吹来的风时,金属丝偏离竖直方向的角度为θ。风力F与θ、m之间的关系式正确的是
A.F=mg sin θ
B.F=mg cos θ
C.F=mg tan θ
D.F=
√
对金属球受力分析,如图所示,金属球受到重力、拉力和风力共3个力作用,根据共点力平衡条件可知,拉力和风力的合力与重力平衡,由几何关系得到F=mg tan θ,C正确。
返回
课 时 测 评
1.若某一物体受共点力作用处于平衡状态,则该物体
A.一定是静止的
B.一定做匀速直线运动
C.所受各共点力的合力可能不为零
D.所受各共点力的合力为零
√
物体处于平衡状态时,物体可能静止或做匀速直线运动,选项A、B错误;此时所受各共点力的合力一定为零,选项C错误,D正确。
2.(2024·浙江杭州余杭二中测试)树懒是一种懒得出奇的哺乳动物,什么事都懒得做,甚至懒得去吃,懒得去玩耍,能耐饥一个月以上,非得活动不可时,动作也是懒洋洋的,极其迟缓。树懒静止倒挂在树干上时,树干给树懒的力的方向为
A.垂直于树干向上
B.沿树干向上
C.竖直向上
D.树干形变复杂,无法判断力的方向
√
树懒静止倒挂在树干上,则所受的重力与树干对它的作用力平衡,可知树干给树懒的力的方向为竖直向上,故选C。
3.(2022·重庆高考)如图所示,吸附在竖直玻璃上质量为m的擦窗工具,在竖直平面内受重力、拉力和摩擦力(图中未画出摩擦力)的共同作用做匀速直线运动。若拉力大小与重力大小相等,方向水平向右,重力加速度为g,则擦窗工具所受摩擦力
A.大小等于mg B.大小等于 mg
C.方向竖直向上 D.方向水平向左
√
擦窗工具做匀速直线运动,所受合力为0,则摩擦力大小等于重力和拉力的合力,拉力大小等于重力,则f= mg,方向斜向左上方与水平方向夹角为45°,故B正确。
4.在如图所示的四幅图中,AB、BC均为轻质杆,各图中杆的A、C端都通过铰链与墙连接,两杆都在B处由铰链相连接。下列说法正确的是
A.图中的AB杆可以用与之等长的轻绳代替的有甲、乙
B.图中的AB杆可以用与之等长的轻绳代替的有甲、丙、丁
C.图中的BC杆可以用与之等长的轻绳代替的有乙、丙
D.图中的BC杆可以用与之等长的轻绳代替的有乙、丁
√
轻绳只能产生拉力,而杆可产生拉力也可产生推力,故能用绳代替杆的情况是杆中的力为拉力。题图甲、丙、丁中AB杆产生的是拉力,题图丙中BC杆产生的是拉力,B正确。
5.如图所示,在水平天花板上用绳AC、BC和CD吊起一个物体,使其处于静止状态,结点为C,绳子的长度分别为AC=4 dm,BC=3 dm,悬点A、B间距为5 dm。则AC绳、BC绳、CD绳上的拉力大小之比为
A.20∶15∶12 B.4∶3∶5
C.3∶4∶5 D.因CD绳长未知,故无法确定
√
对三条绳的结点C进行受力分析,如图所示,由共点力平衡的条件知,AC、BC绳上拉力的合力与CD绳上的拉力等大反向。由几何关系知,AC绳、BC绳、CD绳上的拉力大小之比为3∶4∶5,所以C正确。
6.(多选)一个大人拉着载有两个小孩的小车(其拉杆可自由转动)沿水平地面匀速直线前进,则对小孩和车下列说法正确的是
A.拉力的水平分力等于小孩和车所受的合力
B.拉力与摩擦力的合力大小等于重力大小
C.拉力与摩擦力的合力方向竖直向上
D.小孩和车所受的合力为零
√
小孩和车做匀速直线运动,故小孩和车所受的合力为零。小孩和车整体受重力、支持力、拉力和摩擦力,根据共点力平衡条件,拉力的水平分力等于小孩和车所受的摩擦力,故A错误,D正确;拉力、摩擦力的合力与重力、支持力的合力平衡,重力、支持力的合力竖直,故拉力与摩擦力的合力方向竖直向上,故B错误,C正确。
√
7.放假了,小明斜拉着拉杆箱离开校园。如图所示,小明的拉力大小为F,方向沿拉杆斜向上,与水平地面夹角为θ。与拉杆箱竖直静止在水平地面且不受拉力相比,此时水平地面对拉杆箱的支持力
A.减少了F sin θ B.增大了F sin θ
C.减少了F cos θ D.增大了F cos θ
√
以箱子为研究对象,受到重力、支持力、拉力和摩擦力,如图所示,没有拉力时,支持力等于重力mg;有拉力F时,支持力为N=mg-F sin θ,所以支持力减少了F sin θ,故A正确。
8.如图所示的几种情况中,不计绳、弹簧测力计、各滑轮的质量,不计一切摩擦,物体质量都为m,且均处于静止状态,有关角度图中已标出。弹簧测力计的示数分别为FA、FB、FC、FD,则
A.FB>FD>FA>FC B.FD>FC>FB>FA
C.FD>FB>FA>FC D.FC>FD>FB>FA
√
9.(多选)将沙桶P用细绳系在C点,如图所示,在两沙桶中装上一定质量的沙子,沙桶(含沙子)P、Q的总质量分别为m1、m2,系统平衡时,∠ACB=90°、∠CAB=60°,忽略滑轮的大小以及摩擦。则下列说法正确的是
A.m1∶m2=1∶1
B.m1∶m2=2∶1
C.若在两桶内增加相同质量的沙子,C点的位置上升
D.若在两桶内增加相同质量的沙子,C点的位置保持不变
√
√
以结点C为研究对象,受力分析如图所示,其中F=m1g、FB=m2g,由力的平衡条件可知FA=F cos 30°=m1g cos 30°,由几何关系可知FA=
,联立解得m1∶m2=2∶1,选项A错误,B正确;由以上分析可知,若在两桶内增加相同质量的沙子,则两沙桶(含沙子)质量的比值会小于2,则Q桶向下移动,C点的位置上升,选项C正确,D错误。
10.如图所示,两个质量为m1的小球套在竖直放置的光滑支架上,支架的夹角为120°,用轻绳将两球与质量为m2的小球连接,轻绳与支架构成一个菱形,则m1∶m2为
A.1∶1 B.1∶2
C.1∶ D. ∶2
√
将小球m2受到的重力按作用效果根据平行四边形定则进行分解,如图所示,由几何知识得T=m2g;对m1受力分析,由平衡条件,在沿支架的方向上有m1g sin 30°=T sin 30°,可得T=m1g,则m1∶m2=1∶1,故A正确。
11.(10分)(2024·山东德州高一月考)如图所示,在倾角θ=37°的固定斜面上,用一水平力F推一质量m=10 kg的物体,欲使物体沿斜面做匀速直线运动,已知物体与斜面间的动摩擦因数μ=0.2,求F的大小(结果保留到个位,sin 37°=0.6,cos 37°=0.8,g取10 m/s2)。
答案:112 N或48 N
若物体沿斜面向上做匀速直线运动,对物体受力析如图甲所示
根据平衡条件得
F cos θ=f+mg sin θ
N=mg cos θ+F sin θ
又f=μN
解得F≈112 N;
若物体沿斜面向下做匀速直线运动,对物体受力析如图乙所示
根据平衡条件得
F cos θ+f′=mg sin θ
N′= F sin θ+mg cos θ
又f′=μN′
解得F≈48 N。
12.(10分)如图所示,A球和B球用轻绳相连,静止在光滑的圆柱面上,若A球的质量为m,则B球的质量为多少?(A、B两球可视为质点,sin 37°=0.6,sin 53°=0.8)
答案: m
解析:球很小,可认为绳拉球的方向在大圆的切线方向上。分别对A、B进行受力分析如图
对A:mgsin 37°=FA
对B:Mgsin 53°=FB
又FA=FB
联立解得M= m。
返回
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
