天津市天华高级中学2024-2025学年高一下学期第二次阶段性考试数学试卷(图片版,含部分答案)
文档属性
| 名称 | 天津市天华高级中学2024-2025学年高一下学期第二次阶段性考试数学试卷(图片版,含部分答案) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-28 18:33:15 | ||
图片预览



文档简介
天津市天华高级中学 2024-2025 学年高一下学期第
二次阶段性考试数学试卷
一、单选题
1. 若复数 z满足 ,则 z的共轭复数在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2. 已知向量 , ,则 ( )
A. B.1 C. D.2
3. 如图为 水平放置的直观图,其中 , ,那么原
的面积是( )
A. B. D.2
C.
4. 设 的内角 、 、 的对边分别为 ,,,已知 , , ,
则 等于( )
A. B. C. D.
5. 攒尖是中国古代建筑中屋顶的一种结构形式,宋代称为撮尖,清代称为攒尖.
通常有圆形攒尖,三角攒尖,四角攒尖,八角攒尖,也有单檐和重檐之分,多见于亭
阁式建筑,园林建筑.如图所示的建筑屋顶是圆形攒尖,可近似看作一个圆锥,已
知其轴截面是底边长为 m,顶角为 的等腰三角形,则该屋顶的面积约为( ).
2 2B. m 2 2A. m C. m D. m
6. 已知 为两个不同的平面, 为三条不同的直线,则下列结论中正确的
是( )
A.若 ,则 B.若 ,则
C.若 ,且 ,则 D.若 ,且 ,则
7. 已知向量 , 是两个不共线的向量, 与 共线,则
( )
A.2 B. C. D.
8. 在 中,角 ,, 的对边分别为 ,,,若 , ,
则 是( )
A.钝角三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
9. 底面边长为 的正四棱锥被平行于其底面的平面所截,截去一个底面边长为
,高为 3 的正四棱锥,所得棱台的体积为( )
A.28 B.58 C.56 D.
二、填空题
10. i 是虚数单位,化简 的结果为__________________.
11. 某市有大型超市 200 家、中型超市 400 家、小型超市 1400 家.为掌握各类
超市的营业情况,现按分层抽样方法抽取一个容量为 100 的样本,应抽取中型超
市__________家.
12. 已知 ,且 ,则 __________.
13. 在正方体 中, ,则该正方体外接球的表面积为
______.
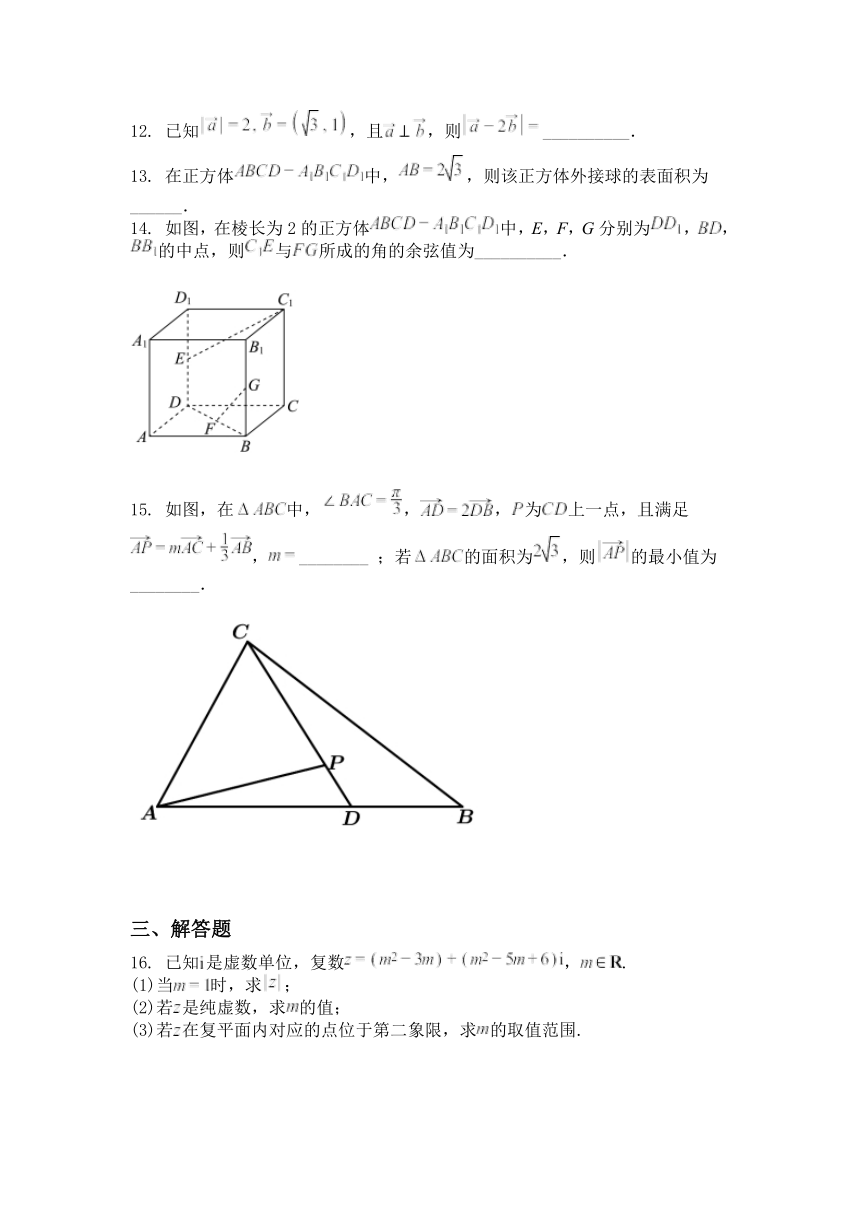
14. 如图,在棱长为 2的正方体 中,E,F,G分别为 , ,
的中点,则 与 所成的角的余弦值为__________.
15. 如图,在 中, , , 为 上一点,且满足
, ________ ;若 的面积为 ,则 的最小值为
________.
三、解答题
16. 已知 是虚数单位,复数 , .
(1)当 时,求 ;
(2)若 是纯虚数,求 的值;
(3)若 在复平面内对应的点位于第二象限,求 的取值范围.
17. 在 的内角 , , 所对边的长分别是 , , ,已知 , ,
.
(1)求 的值;
(2)求 的值;
(3)求 的值.
18. 已知 的内角 A,B,C所对的边分别为 a,b,c,向量 ,
,且 .
(1)求角 A的大小;
(2)若 , ,求边 c和 的面积.
19. 如图,在三棱柱 中,侧面 , 均为正方形,
, ,点 是棱的 中点.
(1)求证: 平面 ;
(2)求 到平面 的距离.
20. 如图,在四面体 中, 是等边三角形,平面 平面 ,点
为棱 的中点, , , .
(1)求证: 平面 ;
(2)求直线 与平面 所成角的正弦值.
天津市天华高级中学 2024-2025 学年高一下学期第二次阶段性考试数学试卷
整体难度:较易
考试范围:复数、平面向量、空间向量与立体几何、三角函数与解三角形、计数原理与概率
统计
试卷题型
题型 数量
单选题 9
填空题 6
解答题 5
试卷难度
难度 题数
容易 7
较易 7
适中 6
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.85 判断复数对应的点所在的象限;复数加减法的代数运算;共轭复数的概念及计算
2 0.94 数量积的坐标表示
3 0.85 斜二测画法中有关量的计算
4 0.94 余弦定理解三角形
5 0.94 圆锥表面积的有关计算
线面关系有关命题的判断;面面关系有关命题的判断;判断线面平行;线面平行
6 0.85
的性质
7 0.65 已知向量共线(平行)求参数
8 0.65 正弦定理边角互化的应用;正、余弦定理判定三角形形状
9 0.94 锥体体积的有关计算;台体体积的有关计算
二、填空题
10 0.94 复数的除法运算
11 0.85 抽样比、样本总量、各层总数、总体容量的计算
12 0.94 已知数量积求模;向量模的坐标表示
13 0.94 球的表面积的有关计算;多面体与球体内切外接问题
14 0.65 异面直线夹角的向量求法
15 0.65 已知数量积求模;利用平面向量基本定理求参数
三、解答题
16 0.85 已知复数的类型求参数;根据复数对应坐标的特点求参数;求复数的模
用和、差角的余弦公式化简、求值;余弦定理解三角形;已知正(余)弦求余(正)
17 0.85
弦;正弦定理解三角形
18 0.85 正弦定理边角互化的应用;余弦定理解三角形;三角形面积公式及其应用
19 0.65 证明线面平行;求点面距离
20 0.65 求线面角;面面垂直证线面垂直
知识点分析
序号 知识点 对应题号
1 复数 1,10,16
2 平面向量 2,7,12,15
3 空间向量与立体几何 3,5,6,9,13,14,19,20
4 三角函数与解三角形 4,8,17,18
5 计数原理与概率统计 11
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
第 20 题:
二次阶段性考试数学试卷
一、单选题
1. 若复数 z满足 ,则 z的共轭复数在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2. 已知向量 , ,则 ( )
A. B.1 C. D.2
3. 如图为 水平放置的直观图,其中 , ,那么原
的面积是( )
A. B. D.2
C.
4. 设 的内角 、 、 的对边分别为 ,,,已知 , , ,
则 等于( )
A. B. C. D.
5. 攒尖是中国古代建筑中屋顶的一种结构形式,宋代称为撮尖,清代称为攒尖.
通常有圆形攒尖,三角攒尖,四角攒尖,八角攒尖,也有单檐和重檐之分,多见于亭
阁式建筑,园林建筑.如图所示的建筑屋顶是圆形攒尖,可近似看作一个圆锥,已
知其轴截面是底边长为 m,顶角为 的等腰三角形,则该屋顶的面积约为( ).
2 2B. m 2 2A. m C. m D. m
6. 已知 为两个不同的平面, 为三条不同的直线,则下列结论中正确的
是( )
A.若 ,则 B.若 ,则
C.若 ,且 ,则 D.若 ,且 ,则
7. 已知向量 , 是两个不共线的向量, 与 共线,则
( )
A.2 B. C. D.
8. 在 中,角 ,, 的对边分别为 ,,,若 , ,
则 是( )
A.钝角三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
9. 底面边长为 的正四棱锥被平行于其底面的平面所截,截去一个底面边长为
,高为 3 的正四棱锥,所得棱台的体积为( )
A.28 B.58 C.56 D.
二、填空题
10. i 是虚数单位,化简 的结果为__________________.
11. 某市有大型超市 200 家、中型超市 400 家、小型超市 1400 家.为掌握各类
超市的营业情况,现按分层抽样方法抽取一个容量为 100 的样本,应抽取中型超
市__________家.
12. 已知 ,且 ,则 __________.
13. 在正方体 中, ,则该正方体外接球的表面积为
______.
14. 如图,在棱长为 2的正方体 中,E,F,G分别为 , ,
的中点,则 与 所成的角的余弦值为__________.
15. 如图,在 中, , , 为 上一点,且满足
, ________ ;若 的面积为 ,则 的最小值为
________.
三、解答题
16. 已知 是虚数单位,复数 , .
(1)当 时,求 ;
(2)若 是纯虚数,求 的值;
(3)若 在复平面内对应的点位于第二象限,求 的取值范围.
17. 在 的内角 , , 所对边的长分别是 , , ,已知 , ,
.
(1)求 的值;
(2)求 的值;
(3)求 的值.
18. 已知 的内角 A,B,C所对的边分别为 a,b,c,向量 ,
,且 .
(1)求角 A的大小;
(2)若 , ,求边 c和 的面积.
19. 如图,在三棱柱 中,侧面 , 均为正方形,
, ,点 是棱的 中点.
(1)求证: 平面 ;
(2)求 到平面 的距离.
20. 如图,在四面体 中, 是等边三角形,平面 平面 ,点
为棱 的中点, , , .
(1)求证: 平面 ;
(2)求直线 与平面 所成角的正弦值.
天津市天华高级中学 2024-2025 学年高一下学期第二次阶段性考试数学试卷
整体难度:较易
考试范围:复数、平面向量、空间向量与立体几何、三角函数与解三角形、计数原理与概率
统计
试卷题型
题型 数量
单选题 9
填空题 6
解答题 5
试卷难度
难度 题数
容易 7
较易 7
适中 6
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.85 判断复数对应的点所在的象限;复数加减法的代数运算;共轭复数的概念及计算
2 0.94 数量积的坐标表示
3 0.85 斜二测画法中有关量的计算
4 0.94 余弦定理解三角形
5 0.94 圆锥表面积的有关计算
线面关系有关命题的判断;面面关系有关命题的判断;判断线面平行;线面平行
6 0.85
的性质
7 0.65 已知向量共线(平行)求参数
8 0.65 正弦定理边角互化的应用;正、余弦定理判定三角形形状
9 0.94 锥体体积的有关计算;台体体积的有关计算
二、填空题
10 0.94 复数的除法运算
11 0.85 抽样比、样本总量、各层总数、总体容量的计算
12 0.94 已知数量积求模;向量模的坐标表示
13 0.94 球的表面积的有关计算;多面体与球体内切外接问题
14 0.65 异面直线夹角的向量求法
15 0.65 已知数量积求模;利用平面向量基本定理求参数
三、解答题
16 0.85 已知复数的类型求参数;根据复数对应坐标的特点求参数;求复数的模
用和、差角的余弦公式化简、求值;余弦定理解三角形;已知正(余)弦求余(正)
17 0.85
弦;正弦定理解三角形
18 0.85 正弦定理边角互化的应用;余弦定理解三角形;三角形面积公式及其应用
19 0.65 证明线面平行;求点面距离
20 0.65 求线面角;面面垂直证线面垂直
知识点分析
序号 知识点 对应题号
1 复数 1,10,16
2 平面向量 2,7,12,15
3 空间向量与立体几何 3,5,6,9,13,14,19,20
4 三角函数与解三角形 4,8,17,18
5 计数原理与概率统计 11
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
第 20 题:
同课章节目录
