期末评估测试卷(含答案)2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 期末评估测试卷(含答案)2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 275.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-28 22:27:36 | ||
图片预览



文档简介
期末评估测试卷
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在实数-,0,-,506,π,0.1中,无理数有 ( )
A.2个 B.3个 C.4个 D.5个
2.下列命题是真命题的是 ( )
A.同角的余角相等
B.相等的角是对顶角
C.垂直于同一条直线的两条直线平行
D.内错角相等
3.下表是10支不同型号签字笔的相关信息,则1支签字笔的平均价格是 ( )
型号 A B C
价格/(元/支) 1 1.5 2
数量/支 3 2 5
A.1.4元 B.1.5元 C.1.6元 D.1.7元
4.小颖同学将一根铁丝剪成九段,分成三个组:①1 cm,2 cm,3 cm;②6 cm,8 cm,10 cm;③9 cm,40 cm,41 cm。分别以每组铁丝围成三角形,能构成直角三角形的有 ( )
A.② B.①② C.①③ D.②③
5.(2024甘孜州中考)在平面直角坐标系中,一次函数y=x+1的图象不经过的象限为 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如图是某次象棋对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,那么在同一平面直角坐标系下,图象经过棋子“帅”和“马”所在的点的一次函数表达式为 ( )
A.y=x+1 B.y=x-1
C.y=2x+1 D.y=2x-1
7.(2024赤峰中考)用1块A型钢板可制成3块C型钢板和4块D型钢板;用1块B型钢板可制成5块C型钢板和2块D型钢板。现在需要58块C型钢板、40块D型钢板,则恰好用A型钢板、B型钢板各多少块 如果设用A型钢板x块,用B型钢板y块,那么可列方程组为 ( )
A. B.
C. D.
8.某社区为了打造“书香社区”,丰富小区居民的业余文化生活,计划出资500元全部用于采购A,B,C三种图书,A种每本30元,B种每本25元,C种每本20元,其中A种图书至少买5本,最多买6本(三种图书都要买),此次采购的方案有 ( )
A.5种 B.6种 C.7种 D.8种
9.已知正比例函数y=kx(k≠0)的函数值y随x值的增大而减小,则一次函数y=x+k的图象大致是( )
A B C D
10.如图,已知∠F+∠FGD=80°(其中∠F>∠FGD),添加以下一个条件:①∠FEB+2∠FGD=80°;②∠F+∠FGC=180°;③∠F+∠FEA=180°;④∠FGC-∠F=100°。其中能证明AB∥CD的条件有 ( )
A.0个 B.1个 C.2个 D.3个
二、填空题(本题共5小题,每小题3分,共15分)
11.的算术平方根是 ;-的立方根是 。
12.点A(5,-3)关于y轴的对称点的坐标是 。
13.《周礼·考工记》中记载有“……半矩谓之宣(xuān),一宣有半谓之欘(zhú)……”。意思是“……直角的一半的角叫作宣,一宣半的角叫作欘……”,即1宣= 矩,1欘=1 宣(其中,1矩=90°)。
问题:图1为中国古代一种强弩图,图2为这种强弩图的部分组件的示意图,若∠A=1矩,∠B=1欘,则∠C= °。
图1 图2
14.将一个三角尺(∠A=30°)按如图所示的位置摆放,直线a∥b,若∠ABD=20°,则∠α的度数是 。
15.一次函数y=kx+b(k,b为常数,k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=-3的解为 。
三、解答题(本题共8小题,共75分,解答应写出文字说明、演算步骤或推理过程)
16.(8分)如图是某单位的平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1)。
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出点A的位置;
(3)建筑物B在大门北偏东45°的方向,并且B在花坛的正北方向,请在图中标出点B的位置并写出点B的坐标。
17.(8分)(1)计算:+(π-3)0;
(2)解方程组:
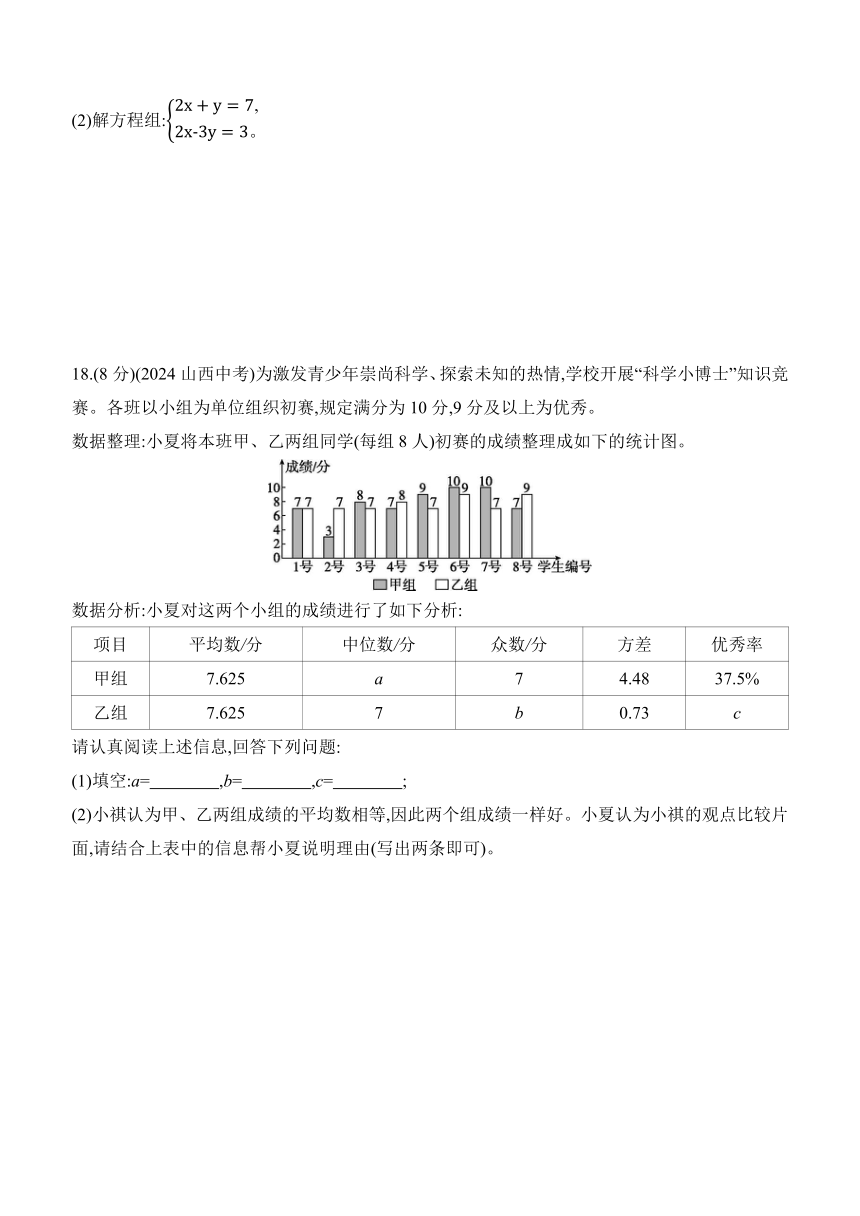
18.(8分)(2024山西中考)为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛。各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀。
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图。
数据分析:小夏对这两个小组的成绩进行了如下分析:
项目 平均数/分 中位数/分 众数/分 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:a= ,b= ,c= ;
(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好。小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可)。
19.(8分)以下表示小丽到水果店购买2个单价相同的椰子和10个单价相同的柠檬的经过。
根据上面两人对话,求原来椰子和柠檬的单价各是多少。(注:打九折即原价的90%)
20.(8分)小明制作了一张面积为256 cm2的正方形贺卡想寄给朋友。现有一个长方形信封如图所示,长、宽之比为3∶2,面积为420 cm2。
(1)求长方形信封的长和宽;
(2)小明能将贺卡不折叠就放入此信封吗 请通过计算给出判断。
21.(10分)如图,在△ABC中,AB=12,AC=16,BC=20。
(1)判断△ABC的形状,并说明理由;
(2)若P为线段AC上一点,连接BP,且BP=CP,求AP的长。
22.(12分)某市“共富工坊”问海借力,某公司产品销售量得到大幅提升。为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同。看图解答下列问题:
(1)直接写出员工生产多少件产品时,两种方案付给的报酬一样多;
(2)求方案二y关于x的函数表达式;
(3)如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案
23.(13分)(2025周口太康县期末)【问题情境】
在综合实践课上,老师组织班上的同学开展了探究两角之间数量关系的数学活动。如图,已知射线AM∥BN,连接AB,P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,且分别交射线AM于点C,D。
【探索发现】
(1)当∠A=60°时,求证:∠CBD=∠A。
(2)“快乐小组”经过探索后发现:不断改变∠A的度数,∠CBD与∠A始终存在某种数量关系。
①当∠A=40°时,∠CBD= °。
②当∠A=x°时,∠CBD= °(用含x的代数式表示)。
【操作探究】
(3)“智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系。他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变。请写出它们的关系,并说明理由。
【详解答案】
1.A
2.A 解析:A.同角的余角相等,故原命题是真命题,符合题意;B.相等的角不一定是对顶角,故原命题是假命题,不符合题意;C.在同一平面内,垂直于同一条直线的两条直线平行,故原命题是假命题,不符合题意;D.两直线平行,内错角相等,故原命题是假命题,不符合题意。故选A。
3.C 4.D
5.D 解析:令x=0得,y=1,令y=0得,x=-1,所以一次函数的图象经过点(0,1)和(-1,0)。如图所示,所以一次函数的图象不经过第四象限。故选D。
6.A 解析:由“帅”位于点(-2,-1)可得,“马”位于点(1,2)。设图象经过棋子“帅”和“马”所在的点的一次函数表达式为y=kx+b(k≠0)。∴解得∴y=x+1。故选A。
7.C 解析:∵用1块A型钢板可制成3块C型钢板和4块D型钢板,用1块B型钢板可制成5块C型钢板和2块D型钢板,且现在需要58块C型钢板,∴3x+5y=58。∴4x+2y=40。∴根据题意可列方程组故选C。
8.B 解析:当购买5本A种图书时,设购买x本B种图书,y本C种图书,根据题意,得30×5+25x+20y=500。∴x=14-y。又∵x,y均为正整数,∴或或∴当购买5本A种图书时,有3种采购方案。当购买6本A种图书时,设购买m本B种图书,n本C种图书,根据题意,得30×6+25m+20n=500。∴n=16-m。又∵m,n均为正整数,∴或或∴当购买6本A种图书时,有3种采购方案。∴此次采购的方案有3+3=6(种)。故选B。
9.B 解析:∵正比例函数y=kx(k≠0)的函数值y随x值的增大而减小,∴k<0。∵一次函数y=x+k的一次项系数大于0,常数项小于0,∴一次函数y=x+k的图象经过第一、三、四象限。故选B。
10.B 解析:①如图,过点F作FH∥CD,则∠HFG=∠FGD。∵∠EFG=∠EFH+∠HFG,∠EFG+∠FGD=80°,∴∠EFH+2∠FGD=80°。∵∠FEB+2∠FGD=80°,∴∠EFH=∠FEB。∴AB∥FH。∴AB∥CD。故①符合题意。②∵∠EFG+∠FGC=180°,∴CD∥FE。故②不符合题意。③∵∠EFG+∠FEA=180°,∴AB∥FG。故③不符合题意。④∵∠FGC-∠EFG=100°,∠EFG+∠FGD=80°,∴∠FGC-∠EFG+∠EFG+∠FGD=100°+80°。∴∠FGC+∠FGD=180°。故④不符合题意。综上所述,能证明AB∥CD的是①。故选B。
11. -2 解析:的算术平方根是;-=-8,其立方根是-2。
12.(-5,-3)
13.22.5 解析:∵1宣= 矩,1欘=1 宣,1矩=90°,∠A=1矩,∠B=1欘,∴∠A=90°,∠B=×90°=67.5°。∴∠C=180°-∠A-∠B=180°-90°-67.5°=22.5°。
14.50° 解析:∵∠A=30°,∴∠ABC=60°,∠ACB=90°。∵∠ABD=20°,∴∠DBC=60°-20°=40°。∴∠BDC=90°-∠DBC=50°。∵直线a∥b,∴∠α=∠BDC=50°。
15.x=-4 解析:∵一次函数y=kx+b过(2,3),(0,1)两点,∴2k+b=3,b=1,解得k=1。一次函数的表达式为y=x+1,解方程x+1=-3,得x=-4。
16.解:(1)平面直角坐标系如图所示。
(2)点A如图所示。
(3)点B如图所示,点B(0,3)。
17.解:(1)原式=0.5-2++1=1。
(2)
①-②,得4y=4,即y=1。
将y=1代入①,得x=3。
所以原方程组的解是
18.解:(1)7.5 7 25% 解析:a==7.5,b=7,c=×100%=25%。
(2)理由不唯一,例如:①甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,
∴从优秀率的角度看,甲组成绩比乙组好。
②甲组成绩的中位数为7.5分,高于乙组成绩的中位数,
∴从中位数的角度看,甲组成绩比乙组好。
因此,不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面。
19.解:设原来椰子和柠檬的单价分别是x元和y元。根据题意,得
解得
答:原来椰子的单价是25元,柠檬的单价是5元。
20.解:(1)设长方形信封的长为3x cm,宽为2x cm。
根据题意,得3x·2x=420。
∴x=(负值舍去)。
∴3x=3,2x=2。
答:长方形信封的长为3 cm,宽为2 cm。
(2)面积为256 cm2的正方形贺卡的边长是16 cm。
∵70>64,∴>8。
∴2>16,即信封的宽大于正方形贺卡的边长。
答:小明能将这张贺卡不折叠就放入此信封。
21.解:(1)△ABC是直角三角形。理由如下:
在△ABC中,AB=12,AC=16,BC=20,
∵122+162=400=202,
∴AB2+AC2=BC2。∴△ABC是直角三角形。
(2)设AP=x,则BP=CP=16-x。
在Rt△ABP中,∵AB2+AP2=BP2,
∴122+x2=(16-x)2。解得x=3.5。
∴AP的长为3.5。
22.解:(1)员工生产30件产品时,两种方案付给的报酬一样多。
(2)设方案二y关于x的函数表达式为y=kx+b(k≠0)。
将点(0,600),(30,1 200)代入表达式,
得解得
∴方案二y关于x的函数表达式为y=20x+600。
(3)由两方案的图象交点(30,1 200)可知,
若生产件数x的取值范围为0≤x<30,则选择方案二;
若生产件数x=30,则选择两种方案都可以;
若生产件数x的取值范围为x>30,则选择方案一。
23.解:(1)证明:∵AM∥BN,∠A=60°,
∴∠ABN=180°-∠A=120°。
∵BC,BD分别平分∠ABP和∠PBN,
∴∠PBD=∠PBN,∠CBP=∠ABP。
∴∠PBD+∠CBP=(∠PBN+∠ABP)=∠ABN。
∴∠CBD=∠PBD+∠CBP=∠ABN=60°。
∴∠CBD=∠A。
(2)①70 ②90-x
(3)∠APB=2∠ADB。理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠NBD。
∵BD平分∠PBN,
∴∠PBN=2∠NBD=2∠ADB。
∴∠APB=2∠ADB。
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在实数-,0,-,506,π,0.1中,无理数有 ( )
A.2个 B.3个 C.4个 D.5个
2.下列命题是真命题的是 ( )
A.同角的余角相等
B.相等的角是对顶角
C.垂直于同一条直线的两条直线平行
D.内错角相等
3.下表是10支不同型号签字笔的相关信息,则1支签字笔的平均价格是 ( )
型号 A B C
价格/(元/支) 1 1.5 2
数量/支 3 2 5
A.1.4元 B.1.5元 C.1.6元 D.1.7元
4.小颖同学将一根铁丝剪成九段,分成三个组:①1 cm,2 cm,3 cm;②6 cm,8 cm,10 cm;③9 cm,40 cm,41 cm。分别以每组铁丝围成三角形,能构成直角三角形的有 ( )
A.② B.①② C.①③ D.②③
5.(2024甘孜州中考)在平面直角坐标系中,一次函数y=x+1的图象不经过的象限为 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如图是某次象棋对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,那么在同一平面直角坐标系下,图象经过棋子“帅”和“马”所在的点的一次函数表达式为 ( )
A.y=x+1 B.y=x-1
C.y=2x+1 D.y=2x-1
7.(2024赤峰中考)用1块A型钢板可制成3块C型钢板和4块D型钢板;用1块B型钢板可制成5块C型钢板和2块D型钢板。现在需要58块C型钢板、40块D型钢板,则恰好用A型钢板、B型钢板各多少块 如果设用A型钢板x块,用B型钢板y块,那么可列方程组为 ( )
A. B.
C. D.
8.某社区为了打造“书香社区”,丰富小区居民的业余文化生活,计划出资500元全部用于采购A,B,C三种图书,A种每本30元,B种每本25元,C种每本20元,其中A种图书至少买5本,最多买6本(三种图书都要买),此次采购的方案有 ( )
A.5种 B.6种 C.7种 D.8种
9.已知正比例函数y=kx(k≠0)的函数值y随x值的增大而减小,则一次函数y=x+k的图象大致是( )
A B C D
10.如图,已知∠F+∠FGD=80°(其中∠F>∠FGD),添加以下一个条件:①∠FEB+2∠FGD=80°;②∠F+∠FGC=180°;③∠F+∠FEA=180°;④∠FGC-∠F=100°。其中能证明AB∥CD的条件有 ( )
A.0个 B.1个 C.2个 D.3个
二、填空题(本题共5小题,每小题3分,共15分)
11.的算术平方根是 ;-的立方根是 。
12.点A(5,-3)关于y轴的对称点的坐标是 。
13.《周礼·考工记》中记载有“……半矩谓之宣(xuān),一宣有半谓之欘(zhú)……”。意思是“……直角的一半的角叫作宣,一宣半的角叫作欘……”,即1宣= 矩,1欘=1 宣(其中,1矩=90°)。
问题:图1为中国古代一种强弩图,图2为这种强弩图的部分组件的示意图,若∠A=1矩,∠B=1欘,则∠C= °。
图1 图2
14.将一个三角尺(∠A=30°)按如图所示的位置摆放,直线a∥b,若∠ABD=20°,则∠α的度数是 。
15.一次函数y=kx+b(k,b为常数,k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=-3的解为 。
三、解答题(本题共8小题,共75分,解答应写出文字说明、演算步骤或推理过程)
16.(8分)如图是某单位的平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1)。
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出点A的位置;
(3)建筑物B在大门北偏东45°的方向,并且B在花坛的正北方向,请在图中标出点B的位置并写出点B的坐标。
17.(8分)(1)计算:+(π-3)0;
(2)解方程组:
18.(8分)(2024山西中考)为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛。各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀。
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图。
数据分析:小夏对这两个小组的成绩进行了如下分析:
项目 平均数/分 中位数/分 众数/分 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:a= ,b= ,c= ;
(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好。小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可)。
19.(8分)以下表示小丽到水果店购买2个单价相同的椰子和10个单价相同的柠檬的经过。
根据上面两人对话,求原来椰子和柠檬的单价各是多少。(注:打九折即原价的90%)
20.(8分)小明制作了一张面积为256 cm2的正方形贺卡想寄给朋友。现有一个长方形信封如图所示,长、宽之比为3∶2,面积为420 cm2。
(1)求长方形信封的长和宽;
(2)小明能将贺卡不折叠就放入此信封吗 请通过计算给出判断。
21.(10分)如图,在△ABC中,AB=12,AC=16,BC=20。
(1)判断△ABC的形状,并说明理由;
(2)若P为线段AC上一点,连接BP,且BP=CP,求AP的长。
22.(12分)某市“共富工坊”问海借力,某公司产品销售量得到大幅提升。为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同。看图解答下列问题:
(1)直接写出员工生产多少件产品时,两种方案付给的报酬一样多;
(2)求方案二y关于x的函数表达式;
(3)如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案
23.(13分)(2025周口太康县期末)【问题情境】
在综合实践课上,老师组织班上的同学开展了探究两角之间数量关系的数学活动。如图,已知射线AM∥BN,连接AB,P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,且分别交射线AM于点C,D。
【探索发现】
(1)当∠A=60°时,求证:∠CBD=∠A。
(2)“快乐小组”经过探索后发现:不断改变∠A的度数,∠CBD与∠A始终存在某种数量关系。
①当∠A=40°时,∠CBD= °。
②当∠A=x°时,∠CBD= °(用含x的代数式表示)。
【操作探究】
(3)“智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系。他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变。请写出它们的关系,并说明理由。
【详解答案】
1.A
2.A 解析:A.同角的余角相等,故原命题是真命题,符合题意;B.相等的角不一定是对顶角,故原命题是假命题,不符合题意;C.在同一平面内,垂直于同一条直线的两条直线平行,故原命题是假命题,不符合题意;D.两直线平行,内错角相等,故原命题是假命题,不符合题意。故选A。
3.C 4.D
5.D 解析:令x=0得,y=1,令y=0得,x=-1,所以一次函数的图象经过点(0,1)和(-1,0)。如图所示,所以一次函数的图象不经过第四象限。故选D。
6.A 解析:由“帅”位于点(-2,-1)可得,“马”位于点(1,2)。设图象经过棋子“帅”和“马”所在的点的一次函数表达式为y=kx+b(k≠0)。∴解得∴y=x+1。故选A。
7.C 解析:∵用1块A型钢板可制成3块C型钢板和4块D型钢板,用1块B型钢板可制成5块C型钢板和2块D型钢板,且现在需要58块C型钢板,∴3x+5y=58。∴4x+2y=40。∴根据题意可列方程组故选C。
8.B 解析:当购买5本A种图书时,设购买x本B种图书,y本C种图书,根据题意,得30×5+25x+20y=500。∴x=14-y。又∵x,y均为正整数,∴或或∴当购买5本A种图书时,有3种采购方案。当购买6本A种图书时,设购买m本B种图书,n本C种图书,根据题意,得30×6+25m+20n=500。∴n=16-m。又∵m,n均为正整数,∴或或∴当购买6本A种图书时,有3种采购方案。∴此次采购的方案有3+3=6(种)。故选B。
9.B 解析:∵正比例函数y=kx(k≠0)的函数值y随x值的增大而减小,∴k<0。∵一次函数y=x+k的一次项系数大于0,常数项小于0,∴一次函数y=x+k的图象经过第一、三、四象限。故选B。
10.B 解析:①如图,过点F作FH∥CD,则∠HFG=∠FGD。∵∠EFG=∠EFH+∠HFG,∠EFG+∠FGD=80°,∴∠EFH+2∠FGD=80°。∵∠FEB+2∠FGD=80°,∴∠EFH=∠FEB。∴AB∥FH。∴AB∥CD。故①符合题意。②∵∠EFG+∠FGC=180°,∴CD∥FE。故②不符合题意。③∵∠EFG+∠FEA=180°,∴AB∥FG。故③不符合题意。④∵∠FGC-∠EFG=100°,∠EFG+∠FGD=80°,∴∠FGC-∠EFG+∠EFG+∠FGD=100°+80°。∴∠FGC+∠FGD=180°。故④不符合题意。综上所述,能证明AB∥CD的是①。故选B。
11. -2 解析:的算术平方根是;-=-8,其立方根是-2。
12.(-5,-3)
13.22.5 解析:∵1宣= 矩,1欘=1 宣,1矩=90°,∠A=1矩,∠B=1欘,∴∠A=90°,∠B=×90°=67.5°。∴∠C=180°-∠A-∠B=180°-90°-67.5°=22.5°。
14.50° 解析:∵∠A=30°,∴∠ABC=60°,∠ACB=90°。∵∠ABD=20°,∴∠DBC=60°-20°=40°。∴∠BDC=90°-∠DBC=50°。∵直线a∥b,∴∠α=∠BDC=50°。
15.x=-4 解析:∵一次函数y=kx+b过(2,3),(0,1)两点,∴2k+b=3,b=1,解得k=1。一次函数的表达式为y=x+1,解方程x+1=-3,得x=-4。
16.解:(1)平面直角坐标系如图所示。
(2)点A如图所示。
(3)点B如图所示,点B(0,3)。
17.解:(1)原式=0.5-2++1=1。
(2)
①-②,得4y=4,即y=1。
将y=1代入①,得x=3。
所以原方程组的解是
18.解:(1)7.5 7 25% 解析:a==7.5,b=7,c=×100%=25%。
(2)理由不唯一,例如:①甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,
∴从优秀率的角度看,甲组成绩比乙组好。
②甲组成绩的中位数为7.5分,高于乙组成绩的中位数,
∴从中位数的角度看,甲组成绩比乙组好。
因此,不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面。
19.解:设原来椰子和柠檬的单价分别是x元和y元。根据题意,得
解得
答:原来椰子的单价是25元,柠檬的单价是5元。
20.解:(1)设长方形信封的长为3x cm,宽为2x cm。
根据题意,得3x·2x=420。
∴x=(负值舍去)。
∴3x=3,2x=2。
答:长方形信封的长为3 cm,宽为2 cm。
(2)面积为256 cm2的正方形贺卡的边长是16 cm。
∵70>64,∴>8。
∴2>16,即信封的宽大于正方形贺卡的边长。
答:小明能将这张贺卡不折叠就放入此信封。
21.解:(1)△ABC是直角三角形。理由如下:
在△ABC中,AB=12,AC=16,BC=20,
∵122+162=400=202,
∴AB2+AC2=BC2。∴△ABC是直角三角形。
(2)设AP=x,则BP=CP=16-x。
在Rt△ABP中,∵AB2+AP2=BP2,
∴122+x2=(16-x)2。解得x=3.5。
∴AP的长为3.5。
22.解:(1)员工生产30件产品时,两种方案付给的报酬一样多。
(2)设方案二y关于x的函数表达式为y=kx+b(k≠0)。
将点(0,600),(30,1 200)代入表达式,
得解得
∴方案二y关于x的函数表达式为y=20x+600。
(3)由两方案的图象交点(30,1 200)可知,
若生产件数x的取值范围为0≤x<30,则选择方案二;
若生产件数x=30,则选择两种方案都可以;
若生产件数x的取值范围为x>30,则选择方案一。
23.解:(1)证明:∵AM∥BN,∠A=60°,
∴∠ABN=180°-∠A=120°。
∵BC,BD分别平分∠ABP和∠PBN,
∴∠PBD=∠PBN,∠CBP=∠ABP。
∴∠PBD+∠CBP=(∠PBN+∠ABP)=∠ABN。
∴∠CBD=∠PBD+∠CBP=∠ABN=60°。
∴∠CBD=∠A。
(2)①70 ②90-x
(3)∠APB=2∠ADB。理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠NBD。
∵BD平分∠PBN,
∴∠PBN=2∠NBD=2∠ADB。
∴∠APB=2∠ADB。
同课章节目录
