河北省邯郸市三龙育华中学2024-2025学年高二下学期期中数学试题(PDF版,含解析)
文档属性
| 名称 | 河北省邯郸市三龙育华中学2024-2025学年高二下学期期中数学试题(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-28 22:40:47 | ||
图片预览




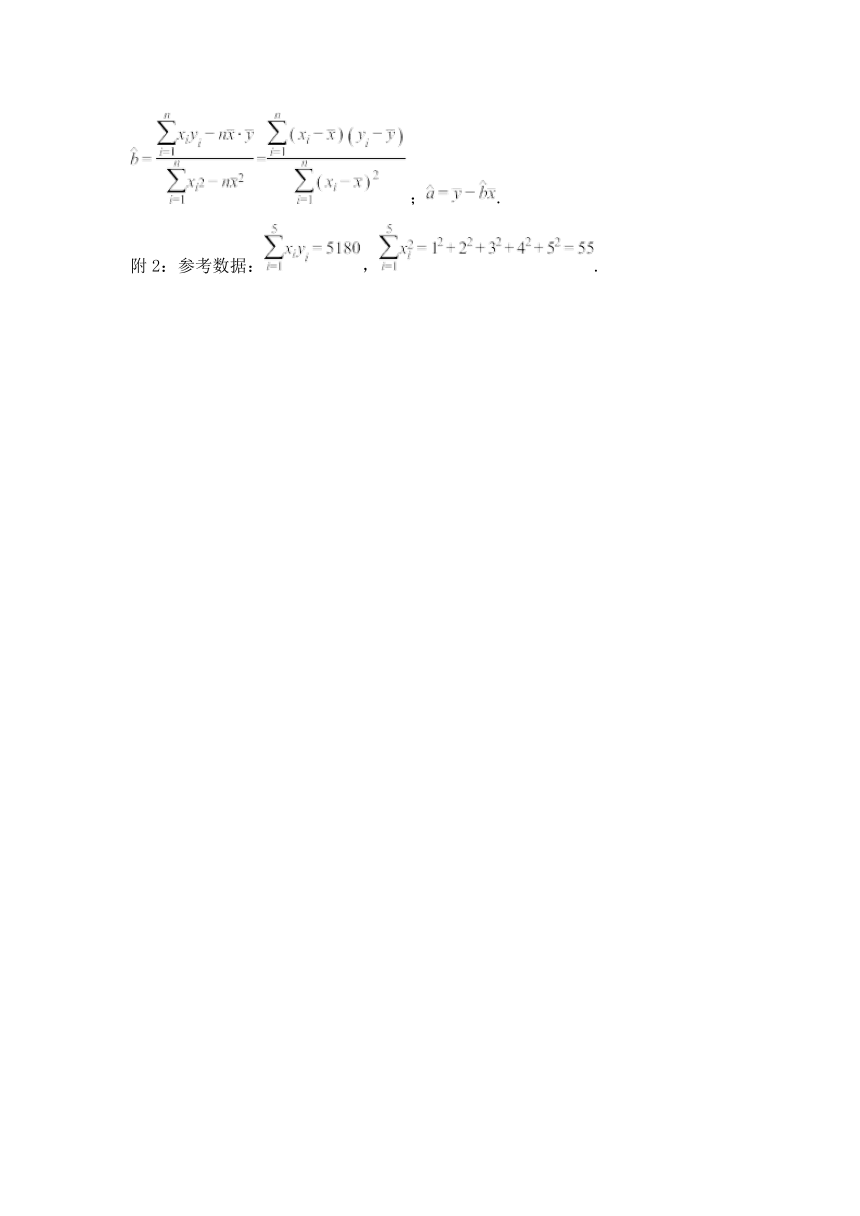
文档简介
河北省邯郸市三龙育华中学 2024-2025 学年高二下
学期期中数学试题
一、单选题
1. 函数 的导数为( )
A. B. C. D.
2. 某人进行投篮训练,最多投篮 4次,命中一次就停止投篮,记投篮次数为 ,
则 表示的试验结果是( )
A.第 4次投篮命中 B.第 4次投篮未命中
C.前 3次投篮均未命中 D.投篮命中 4次
3. 在一次数学考试中,某校学生的成绩 ,且 .若从
该校的考生中随机抽取一名学生,则其成绩在区间 内的概率为( )
A.0.1 B.0.2 C.0.3 D.0.4
4. 已知变量 x,y 之间具有线性相关关系,根据 10 对样本数据求得经验回归方
程为 ,若 , ,则 ( )
A. B. C.1 D.1.2
5. 已知函数 , 是函数 的导函数,则 的图像大致
是( )
A. B.
C. D.
6. 中小学每年对在校生实施健康体检.据统计,某校学生大约 的人患色盲,
而该校男同学人数约占总学生数的 ,这些人的色盲率约为 .现从女同学中
任选一人,则此人患色盲的概率为( )
A. B. C. D.
7. 有甲、乙等五人到三家企业去应聘,若每人至多被一家企业录用,每家企业
至少录用其中一人且甲、乙两人不能被同一家企业录用,则不同的录用情况种数
是( )
A.60 B.114 C.278 D.336
8. 已知 且 且 且 ,则( )
A. B. C. D.
二、多选题
9. 已知随机事件 A,B 满足 , , ,则下列说法正
确的是( )
A. B.事件 与事件 相互独立
C. D.
10. 下列说法正确的是( )
A.若随机变量 X 的数学期望 ,则
B.若随机变量 且 ,则
C.在含有 3件次品的 9件产品中,任取 3件, 表示取到的次品数,则
D.若随机变量 ,则
11. 已知函数 ,当 时, 恒成立,则
( )
A. 在 上单调递增
B. 有极大值
C. 的极小值点为
D. 只有一个零点
三、填空题
12. 已知随机变量 的分布列如下表:
_____________
13. 被 9 除所得的余数是__________.
14. 设点 A 在直线 上,点 B 在函数 的图象上,则 的
最小值为____.
四、解答题
15. 某种产品的加工需要经过 、 、 、 、 共 5道工序.
(1)如果 工序不能放在最后,那么有多少种加工顺序?
(2)如果工序 和 工序既不能放在最前,也不能放在最后,那么有多少种加工顺
序?
(3)如果 和 工序相邻, 和 不能相邻,那么有多少种加工顺序?
16. 已知二项式 ,若选条件_____ 填写序号 ,
(1)求展开式中含 的项;
(2)设 ,求展开式中奇数项的系数和.
请在:①只有第 项的二项式系数最大;②第 项与第 项的二项式系数相等;③
所有二项式系数的和为 ,
这三个条件中任选一个,补充在上面问题中的线上,并完成解答.
17. 截至 2025 年 2 月 13 日晚,电影《哪吒之魔童闹海》(《哪吒 2》)总票房(含
预售)已突破 100 亿元,观影人次破 2亿,成为中国影史首部票房破 100 亿且观
影人次破2亿的电影,登顶全球影史单一市场票房榜,暂列全球票房榜第17名.按
照猫眼专业版 AI 预测,其最终票房将达到 153.38 亿,若达成则有望超越电影《星
球大战:原力觉醒》的 150.19 亿票房,排名全球前五.银河影院为了解观众是
否喜欢电影与性别有关,调查了 400 名学生(男女各一半)的选择,发现喜欢该
电影的人数是 300,喜欢该电影的女生比男生少 60 人.
(1)完成下面的 列联表;
喜欢电影 不喜欢电影 总计
女生
男生
总计
(2)根据调查数据回答:有 的把握认为是否喜欢电影与性别有关吗?
附: .
临界值表如下:
0.10 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
18. 已知函数 .
(1)若在 处的切线斜率为 ,求 ;
(2)若 恒成立,求 的取值范围.
19. 中国女排,曾经十度成为世界冠军,铸就了响彻中华的女排精神.女排精神
的具体表现为:扎扎实实,勤学苦练,无所畏惧,顽强拼搏,同甘共苦,团结战
斗,刻苦钻研,勇攀高峰.女排精神对各行各业的劳动者起到了激励、感召和促
进作用,给予全国人民巨大的鼓舞.
(1)看过中国女排的纪录片后,某大学掀起“学习女排精神,塑造健康体魄”
的年度主题活动,一段时间后,学生的身体素质明显提高,将该大学近 5个月体
重超重的人数进行统计,得到如下表格:
月份 x 1 2 3 4 5
体重超重的人数 y 640 540 420 300 200
若该大学体重超重人数 y与月份变量 x(月份变量 x依次为 1,2,3,4,5…)
具有线性相关关系,请预测从第几月份开始该大学体重超重的人数降至 10 人以
下?
(2)在某次排球训练课上,球恰由 A队员控制,此后排球仅在 A队员、B队员
和 C队员三人中传递,已知每当球由 A队员控制时,传给 B队员的概率为 ,传
给 C队员的概率为 ;每当球由 B队员控制时,传给 A队员的概率为 ,传给 C
队员的概率为 ;每当球由 C队员控制时,传给 A队员的概率为 ,传给 B队员
的概率为 .记 , , 为经过 n次传球后球分别恰由 A队员、B队员、C队员
控制的概率.
(i)若 ,B队员控制球的次数为 X,求 ;
(ii)若 , , , , ,
证明: 为等比数列,并判断经过 200 次传球后 A队员控制球的概率与 的
大小.
附 1:回归方程 中斜率和截距的最小二乘估计公式分别为:
; .
附 2:参考数据: , .
河北省邯郸市三龙育华中学 2024-2025 学年高二下学期期中数学试题
整体难度:适中
考试范围:函数与导数、计数原理与概率统计、平面解析几何、数列
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
容易 1
较易 8
适中 9
较难 1
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.94 基本初等函数的导数公式;导数的加减法
2 0.85 判断随机试验中的随机变量
3 0.85 指定区间的概率
4 0.85 根据样本中心点求参数
5 0.85 函数图像的识别;函数奇偶性的定义与判断;利用导数研究函数图象及性质
6 0.85 利用全概率公式求概率
7 0.65 分类加法计数原理;分组分配问题;排列组合综合
8 0.65 用导数判断或证明已知函数的单调性;利用导数证明不等式
二、多选题
9 0.65 计算条件概率;独立事件的判断;独立事件的乘法公式
求离散型随机变量的均值;指定区间的概率;二项分布的方差;求超几何分布的
10 0.65
概率
用导数判断或证明已知函数的单调性;求已知函数的极值;利用导数研究函数的
11 0.65
零点
三、填空题
12 0.85 求离散型随机变量的均值;方差的性质;离散型随机变量的方差与标准差
13 0.65 整除和余数问题
14 0.85 已知切线(斜率)求参数;求点到直线的距离
四、解答题
15 0.65 元素(位置)有限制的排列问题;相邻问题的排列问题;不相邻排列问题
二项展开式的应用;二项式的系数和;二项展开式各项的系数和;奇次项与偶次
16 0.65
项的系数和
17 0.85 卡方的计算
已知切线(斜率)求参数;利用导数研究不等式恒成立问题;由导数求函数的最
18 0.65
值(不含参)
19 0.4 由递推关系证明等比数列;求回归直线方程;求离散型随机变量的均值
知识点分析
序号 知识点 对应题号
1 函数与导数 1,5,8,11,14,18
2 计数原理与概率统计 2,3,4,6,7,9,10,12,13,15,16,17,19
3 平面解析几何 14
4 数列 19
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
学期期中数学试题
一、单选题
1. 函数 的导数为( )
A. B. C. D.
2. 某人进行投篮训练,最多投篮 4次,命中一次就停止投篮,记投篮次数为 ,
则 表示的试验结果是( )
A.第 4次投篮命中 B.第 4次投篮未命中
C.前 3次投篮均未命中 D.投篮命中 4次
3. 在一次数学考试中,某校学生的成绩 ,且 .若从
该校的考生中随机抽取一名学生,则其成绩在区间 内的概率为( )
A.0.1 B.0.2 C.0.3 D.0.4
4. 已知变量 x,y 之间具有线性相关关系,根据 10 对样本数据求得经验回归方
程为 ,若 , ,则 ( )
A. B. C.1 D.1.2
5. 已知函数 , 是函数 的导函数,则 的图像大致
是( )
A. B.
C. D.
6. 中小学每年对在校生实施健康体检.据统计,某校学生大约 的人患色盲,
而该校男同学人数约占总学生数的 ,这些人的色盲率约为 .现从女同学中
任选一人,则此人患色盲的概率为( )
A. B. C. D.
7. 有甲、乙等五人到三家企业去应聘,若每人至多被一家企业录用,每家企业
至少录用其中一人且甲、乙两人不能被同一家企业录用,则不同的录用情况种数
是( )
A.60 B.114 C.278 D.336
8. 已知 且 且 且 ,则( )
A. B. C. D.
二、多选题
9. 已知随机事件 A,B 满足 , , ,则下列说法正
确的是( )
A. B.事件 与事件 相互独立
C. D.
10. 下列说法正确的是( )
A.若随机变量 X 的数学期望 ,则
B.若随机变量 且 ,则
C.在含有 3件次品的 9件产品中,任取 3件, 表示取到的次品数,则
D.若随机变量 ,则
11. 已知函数 ,当 时, 恒成立,则
( )
A. 在 上单调递增
B. 有极大值
C. 的极小值点为
D. 只有一个零点
三、填空题
12. 已知随机变量 的分布列如下表:
_____________
13. 被 9 除所得的余数是__________.
14. 设点 A 在直线 上,点 B 在函数 的图象上,则 的
最小值为____.
四、解答题
15. 某种产品的加工需要经过 、 、 、 、 共 5道工序.
(1)如果 工序不能放在最后,那么有多少种加工顺序?
(2)如果工序 和 工序既不能放在最前,也不能放在最后,那么有多少种加工顺
序?
(3)如果 和 工序相邻, 和 不能相邻,那么有多少种加工顺序?
16. 已知二项式 ,若选条件_____ 填写序号 ,
(1)求展开式中含 的项;
(2)设 ,求展开式中奇数项的系数和.
请在:①只有第 项的二项式系数最大;②第 项与第 项的二项式系数相等;③
所有二项式系数的和为 ,
这三个条件中任选一个,补充在上面问题中的线上,并完成解答.
17. 截至 2025 年 2 月 13 日晚,电影《哪吒之魔童闹海》(《哪吒 2》)总票房(含
预售)已突破 100 亿元,观影人次破 2亿,成为中国影史首部票房破 100 亿且观
影人次破2亿的电影,登顶全球影史单一市场票房榜,暂列全球票房榜第17名.按
照猫眼专业版 AI 预测,其最终票房将达到 153.38 亿,若达成则有望超越电影《星
球大战:原力觉醒》的 150.19 亿票房,排名全球前五.银河影院为了解观众是
否喜欢电影与性别有关,调查了 400 名学生(男女各一半)的选择,发现喜欢该
电影的人数是 300,喜欢该电影的女生比男生少 60 人.
(1)完成下面的 列联表;
喜欢电影 不喜欢电影 总计
女生
男生
总计
(2)根据调查数据回答:有 的把握认为是否喜欢电影与性别有关吗?
附: .
临界值表如下:
0.10 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
18. 已知函数 .
(1)若在 处的切线斜率为 ,求 ;
(2)若 恒成立,求 的取值范围.
19. 中国女排,曾经十度成为世界冠军,铸就了响彻中华的女排精神.女排精神
的具体表现为:扎扎实实,勤学苦练,无所畏惧,顽强拼搏,同甘共苦,团结战
斗,刻苦钻研,勇攀高峰.女排精神对各行各业的劳动者起到了激励、感召和促
进作用,给予全国人民巨大的鼓舞.
(1)看过中国女排的纪录片后,某大学掀起“学习女排精神,塑造健康体魄”
的年度主题活动,一段时间后,学生的身体素质明显提高,将该大学近 5个月体
重超重的人数进行统计,得到如下表格:
月份 x 1 2 3 4 5
体重超重的人数 y 640 540 420 300 200
若该大学体重超重人数 y与月份变量 x(月份变量 x依次为 1,2,3,4,5…)
具有线性相关关系,请预测从第几月份开始该大学体重超重的人数降至 10 人以
下?
(2)在某次排球训练课上,球恰由 A队员控制,此后排球仅在 A队员、B队员
和 C队员三人中传递,已知每当球由 A队员控制时,传给 B队员的概率为 ,传
给 C队员的概率为 ;每当球由 B队员控制时,传给 A队员的概率为 ,传给 C
队员的概率为 ;每当球由 C队员控制时,传给 A队员的概率为 ,传给 B队员
的概率为 .记 , , 为经过 n次传球后球分别恰由 A队员、B队员、C队员
控制的概率.
(i)若 ,B队员控制球的次数为 X,求 ;
(ii)若 , , , , ,
证明: 为等比数列,并判断经过 200 次传球后 A队员控制球的概率与 的
大小.
附 1:回归方程 中斜率和截距的最小二乘估计公式分别为:
; .
附 2:参考数据: , .
河北省邯郸市三龙育华中学 2024-2025 学年高二下学期期中数学试题
整体难度:适中
考试范围:函数与导数、计数原理与概率统计、平面解析几何、数列
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
容易 1
较易 8
适中 9
较难 1
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.94 基本初等函数的导数公式;导数的加减法
2 0.85 判断随机试验中的随机变量
3 0.85 指定区间的概率
4 0.85 根据样本中心点求参数
5 0.85 函数图像的识别;函数奇偶性的定义与判断;利用导数研究函数图象及性质
6 0.85 利用全概率公式求概率
7 0.65 分类加法计数原理;分组分配问题;排列组合综合
8 0.65 用导数判断或证明已知函数的单调性;利用导数证明不等式
二、多选题
9 0.65 计算条件概率;独立事件的判断;独立事件的乘法公式
求离散型随机变量的均值;指定区间的概率;二项分布的方差;求超几何分布的
10 0.65
概率
用导数判断或证明已知函数的单调性;求已知函数的极值;利用导数研究函数的
11 0.65
零点
三、填空题
12 0.85 求离散型随机变量的均值;方差的性质;离散型随机变量的方差与标准差
13 0.65 整除和余数问题
14 0.85 已知切线(斜率)求参数;求点到直线的距离
四、解答题
15 0.65 元素(位置)有限制的排列问题;相邻问题的排列问题;不相邻排列问题
二项展开式的应用;二项式的系数和;二项展开式各项的系数和;奇次项与偶次
16 0.65
项的系数和
17 0.85 卡方的计算
已知切线(斜率)求参数;利用导数研究不等式恒成立问题;由导数求函数的最
18 0.65
值(不含参)
19 0.4 由递推关系证明等比数列;求回归直线方程;求离散型随机变量的均值
知识点分析
序号 知识点 对应题号
1 函数与导数 1,5,8,11,14,18
2 计数原理与概率统计 2,3,4,6,7,9,10,12,13,15,16,17,19
3 平面解析几何 14
4 数列 19
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
同课章节目录
