福建省漳州高新技术产业开发区第二中学2024-2025学年高一下学期第二次质量检测数学试卷(PDF版,含解析)
文档属性
| 名称 | 福建省漳州高新技术产业开发区第二中学2024-2025学年高一下学期第二次质量检测数学试卷(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-28 22:55:45 | ||
图片预览




文档简介
福建省漳州高新技术产业开发区第二中学
2024-2025 学年高一下学期第二次质量检测数学试
卷
一、单选题
1. 在复平面内, 对应的点位于( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 在 中,点 D在边 AB上, .记 ,则 ( )
A. B. C. D.
3. 某学习小组共 5名同学,某次模拟考试的数学成绩平均分数为 112,已知其
中 4名同学的成绩分别为 96,109,120,126,则这 5名同学成绩的第 75 百分
位数是( )
A.112 B.119 C.120 D.121
4. 如图一个水平放置的图形的斜二测直观图是一个底角为 ,腰和上底均为 1
的等腰梯形,则原平面图形的面积是( )
A. B.
C. D.
5. 设 ,为不重合的平面, ,为不重合的直线,则其中正确命题的序号为( )
① , ,则 ;
② , , ,则 ;
③ , , ,则 ;
④ , , ,则 .
A.①③ B.②③ C.②④ D.③④
6. 某中学举行疾病防控知识竞赛,其中某道题甲队答对该题的概率为 ,乙队
和丙队答对该题的概率都是 .若各队答题的结果相互独立且都进行了答题.则
甲、乙、丙三支竞赛队伍中恰有一支队伍答对该题的概率为( )
A. B. C. D.
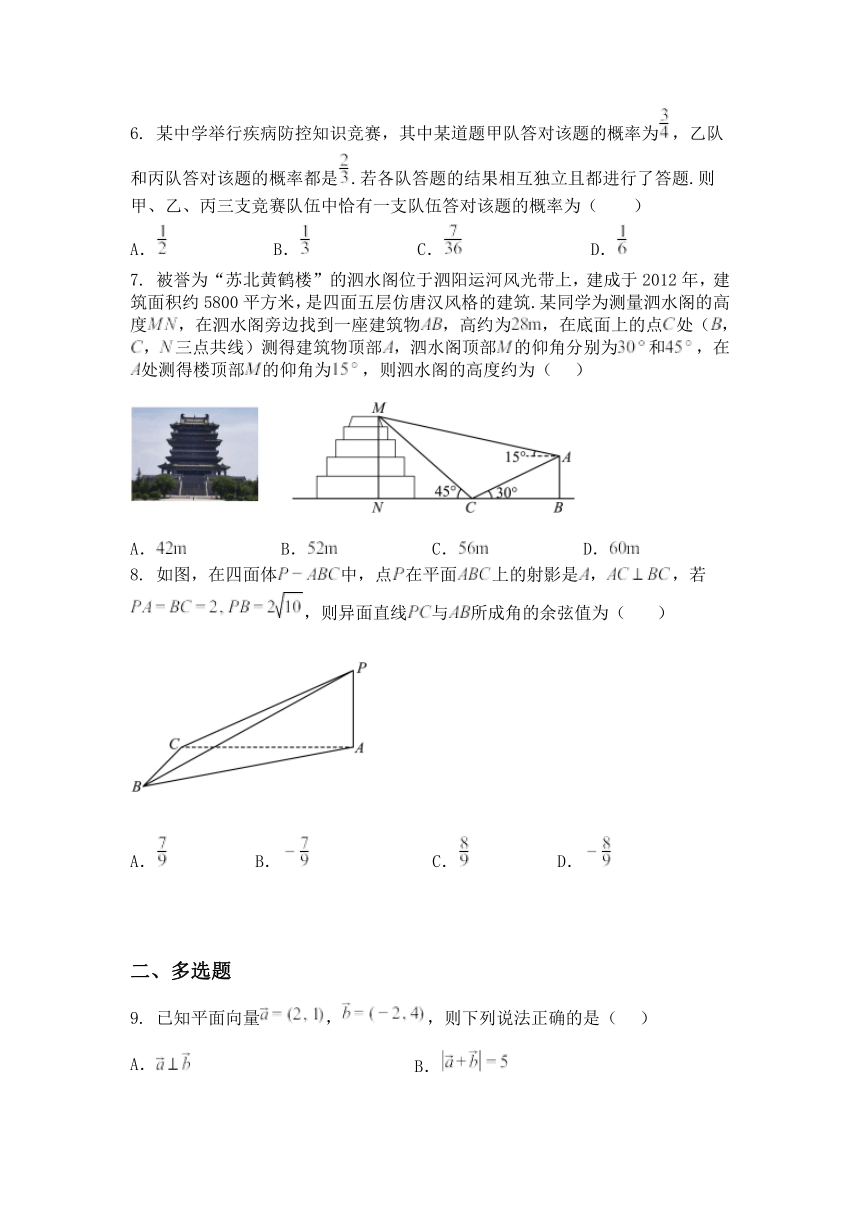
7. 被誉为“苏北黄鹤楼”的泗水阁位于泗阳运河风光带上,建成于 2012 年,建
筑面积约 5800 平方米,是四面五层仿唐汉风格的建筑.某同学为测量泗水阁的高
度 ,在泗水阁旁边找到一座建筑物 ,高约为 ,在底面上的点 处( ,
, 三点共线)测得建筑物顶部 ,泗水阁顶部 的仰角分别为 和 ,在
处测得楼顶部 的仰角为 ,则泗水阁的高度约为( )
A. B. C. D.
8. 如图,在四面体 中,点 在平面 上的射影是 , ,若
,则异面直线 与 所成角的余弦值为( )
A. B. C. D.
二、多选题
9. 已知平面向量 , ,则下列说法正确的是( )
A. B.
C.向量 与 的夹角为钝角 D.向量 在 上的投影向量为
10. 中,角 所对的边分别为 .以下结论中正确的有( )
A.若 ,则 必有两解
B.若 ,则 一定为等腰三角形
C.若 ,则 一定为直角三角形
D.若 ,且该三角形有两解,则 的范围是
11. 如图,在正方体 中,线段 上有两个动点 E,F,且
(m为正常数),则下列结论中正确的是( )
A.
B.线段 上存在点 E,F,使得
C. 的面积与 的面积之比为
D.三棱锥 的体积为定值
三、填空题
12. 若向量 ,且 ,则 ______.
13. 已知古典概型的样本空间 和事件 和 ,其中 , ,
, ,则 ______.
14. 已知正三棱锥 的顶点都在球 O的球面上,其侧棱与底面所成角为 ,
且 ,则球 O的表面积为______________
四、解答题
15. 在 中,角 A,B,C的对边分别为 a,b,c,且 .
(1)求 B;
(2)若 , ,求 的面积.
16. 古人云“民以食为天”,某校为了了解学生食堂服务的整体情况,进一步提
高食堂的服务质量,营造和谐的就餐环境,使同学们能够获得更好的饮食服务.为
此做了一次全校的问卷调查,问卷所涉及的问题均量化成对应的分数(满分 100
分),从所有答卷中随机抽取 100 份分数作为样本,将样本的分数(成绩均为不
低于 40 分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如表
所示的频数分布表.
样本分数段 [40,50) [50,60) [60,70) [70,80) [80,90) [90,100]
频数 5 10 20 a 25 10
(1)求频数分布表中 a的值,并求样本成绩的中位数和平均数;
(2)已知落在[50,60)的分数的平均值为 56,方差是 7;落在[60,70)的分数
的平均值为 65,方差是 4,求两组成绩的总平均数 和总方差 .
17. 江苏省高考目前实行“3+1+2”模式,其中“3”指的是语文 数学,外语这
3门必选科目,“1”指的是考生需要在物理 历史这 2门首选科目中选择 1门,
“2”指的是考生需要在思想政治 地理 化学 生物这 4门再选科目中选择 2门.
已知南京医科大学临床医学类招生选科要求是首选科目为物理,再选科目为化学
生物至少 1门.
(1)从所有选科组合中任意选取 1个,求该选科组合符合南京医科大学临床医学
类招生选科要求的概率;
(2)假设甲 乙 丙三人每人选择任意 1个选科组合是等可能的,求这三人中至少
有两人的选科组合符合南京医科大学临床医学类招生选科要求的概率.
18. 如图,在四棱锥 中, 平面
是 的中点.
(1)证明: 面
(2)证明:平面 平面 ;
(3)求三棱锥 的体积.
19. 如图所示,将一副三角板拼接,使它们有公共边 ,且使两个三角形所在
的平面互相垂直,若
.
(1)求证:平面 平面 ;
(2)求二面角 的平面角的正切值;
(3)求异面直线 与 间的距离.
福建省漳州高新技术产业开发区第二中学 2024-2025 学年高一下学期第二次
质量检测数学试卷
整体难度:适中
考试范围:复数、平面向量、计数原理与概率统计、空间向量与立体几何、三角函数与解三
角形
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
较易 10
适中 9
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.85 在各象限内点对应复数的特征;复数代数形式的乘法运算
2 0.85 用基底表示向量
3 0.85 计算几个数的平均数;总体百分位数的估计
4 0.65 由直观图还原几何图形;斜二测画法中有关量的计算
5 0.85 线面关系有关命题的判断;面面关系有关命题的判断
独立事件的乘法公式;利用互斥事件的概率公式求概率;利用对立事件的概率公
6 0.65
式求概率
7 0.65 正弦定理解三角形;高度测量问题
8 0.65 余弦定理解三角形;求异面直线所成的角
二、多选题
9 0.85 向量夹角的计算;数量积的坐标表示;坐标计算向量的模;求投影向量
10 0.65 正弦定理判定三角形解的个数;正、余弦定理判定三角形形状
11 0.65 锥体体积的有关计算;线面垂直证明线线垂直;异面直线的判定;证明线面垂直
三、填空题
12 0.85 由向量共线(平行)求参数
13 0.85 计算古典概型问题的概率
14 0.85 球的表面积的有关计算;多面体与球体内切外接问题
四、解答题
正弦定理边角互化的应用;三角形面积公式及其应用;用和、差角的正弦公式化
15 0.85
简、求值;正弦定理解三角形
由频率分布直方图估计中位数;平均数的和差倍分性质;由频率分布直方图估计
16 0.85
平均数;估计总体的方差、标准差
17 0.65 利用互斥事件的概率公式求概率;计算古典概型问题的概率
18 0.65 锥体体积的有关计算;证明线面平行;证明面面垂直
19 0.65 求点面距离;证明面面垂直;求二面角
知识点分析
序号 知识点 对应题号
1 复数 1
2 平面向量 2,9,12
3 计数原理与概率统计 3,6,13,16,17
4 空间向量与立体几何 4,5,8,11,14,18,19
5 三角函数与解三角形 7,8,10,15
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
2024-2025 学年高一下学期第二次质量检测数学试
卷
一、单选题
1. 在复平面内, 对应的点位于( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 在 中,点 D在边 AB上, .记 ,则 ( )
A. B. C. D.
3. 某学习小组共 5名同学,某次模拟考试的数学成绩平均分数为 112,已知其
中 4名同学的成绩分别为 96,109,120,126,则这 5名同学成绩的第 75 百分
位数是( )
A.112 B.119 C.120 D.121
4. 如图一个水平放置的图形的斜二测直观图是一个底角为 ,腰和上底均为 1
的等腰梯形,则原平面图形的面积是( )
A. B.
C. D.
5. 设 ,为不重合的平面, ,为不重合的直线,则其中正确命题的序号为( )
① , ,则 ;
② , , ,则 ;
③ , , ,则 ;
④ , , ,则 .
A.①③ B.②③ C.②④ D.③④
6. 某中学举行疾病防控知识竞赛,其中某道题甲队答对该题的概率为 ,乙队
和丙队答对该题的概率都是 .若各队答题的结果相互独立且都进行了答题.则
甲、乙、丙三支竞赛队伍中恰有一支队伍答对该题的概率为( )
A. B. C. D.
7. 被誉为“苏北黄鹤楼”的泗水阁位于泗阳运河风光带上,建成于 2012 年,建
筑面积约 5800 平方米,是四面五层仿唐汉风格的建筑.某同学为测量泗水阁的高
度 ,在泗水阁旁边找到一座建筑物 ,高约为 ,在底面上的点 处( ,
, 三点共线)测得建筑物顶部 ,泗水阁顶部 的仰角分别为 和 ,在
处测得楼顶部 的仰角为 ,则泗水阁的高度约为( )
A. B. C. D.
8. 如图,在四面体 中,点 在平面 上的射影是 , ,若
,则异面直线 与 所成角的余弦值为( )
A. B. C. D.
二、多选题
9. 已知平面向量 , ,则下列说法正确的是( )
A. B.
C.向量 与 的夹角为钝角 D.向量 在 上的投影向量为
10. 中,角 所对的边分别为 .以下结论中正确的有( )
A.若 ,则 必有两解
B.若 ,则 一定为等腰三角形
C.若 ,则 一定为直角三角形
D.若 ,且该三角形有两解,则 的范围是
11. 如图,在正方体 中,线段 上有两个动点 E,F,且
(m为正常数),则下列结论中正确的是( )
A.
B.线段 上存在点 E,F,使得
C. 的面积与 的面积之比为
D.三棱锥 的体积为定值
三、填空题
12. 若向量 ,且 ,则 ______.
13. 已知古典概型的样本空间 和事件 和 ,其中 , ,
, ,则 ______.
14. 已知正三棱锥 的顶点都在球 O的球面上,其侧棱与底面所成角为 ,
且 ,则球 O的表面积为______________
四、解答题
15. 在 中,角 A,B,C的对边分别为 a,b,c,且 .
(1)求 B;
(2)若 , ,求 的面积.
16. 古人云“民以食为天”,某校为了了解学生食堂服务的整体情况,进一步提
高食堂的服务质量,营造和谐的就餐环境,使同学们能够获得更好的饮食服务.为
此做了一次全校的问卷调查,问卷所涉及的问题均量化成对应的分数(满分 100
分),从所有答卷中随机抽取 100 份分数作为样本,将样本的分数(成绩均为不
低于 40 分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如表
所示的频数分布表.
样本分数段 [40,50) [50,60) [60,70) [70,80) [80,90) [90,100]
频数 5 10 20 a 25 10
(1)求频数分布表中 a的值,并求样本成绩的中位数和平均数;
(2)已知落在[50,60)的分数的平均值为 56,方差是 7;落在[60,70)的分数
的平均值为 65,方差是 4,求两组成绩的总平均数 和总方差 .
17. 江苏省高考目前实行“3+1+2”模式,其中“3”指的是语文 数学,外语这
3门必选科目,“1”指的是考生需要在物理 历史这 2门首选科目中选择 1门,
“2”指的是考生需要在思想政治 地理 化学 生物这 4门再选科目中选择 2门.
已知南京医科大学临床医学类招生选科要求是首选科目为物理,再选科目为化学
生物至少 1门.
(1)从所有选科组合中任意选取 1个,求该选科组合符合南京医科大学临床医学
类招生选科要求的概率;
(2)假设甲 乙 丙三人每人选择任意 1个选科组合是等可能的,求这三人中至少
有两人的选科组合符合南京医科大学临床医学类招生选科要求的概率.
18. 如图,在四棱锥 中, 平面
是 的中点.
(1)证明: 面
(2)证明:平面 平面 ;
(3)求三棱锥 的体积.
19. 如图所示,将一副三角板拼接,使它们有公共边 ,且使两个三角形所在
的平面互相垂直,若
.
(1)求证:平面 平面 ;
(2)求二面角 的平面角的正切值;
(3)求异面直线 与 间的距离.
福建省漳州高新技术产业开发区第二中学 2024-2025 学年高一下学期第二次
质量检测数学试卷
整体难度:适中
考试范围:复数、平面向量、计数原理与概率统计、空间向量与立体几何、三角函数与解三
角形
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
较易 10
适中 9
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.85 在各象限内点对应复数的特征;复数代数形式的乘法运算
2 0.85 用基底表示向量
3 0.85 计算几个数的平均数;总体百分位数的估计
4 0.65 由直观图还原几何图形;斜二测画法中有关量的计算
5 0.85 线面关系有关命题的判断;面面关系有关命题的判断
独立事件的乘法公式;利用互斥事件的概率公式求概率;利用对立事件的概率公
6 0.65
式求概率
7 0.65 正弦定理解三角形;高度测量问题
8 0.65 余弦定理解三角形;求异面直线所成的角
二、多选题
9 0.85 向量夹角的计算;数量积的坐标表示;坐标计算向量的模;求投影向量
10 0.65 正弦定理判定三角形解的个数;正、余弦定理判定三角形形状
11 0.65 锥体体积的有关计算;线面垂直证明线线垂直;异面直线的判定;证明线面垂直
三、填空题
12 0.85 由向量共线(平行)求参数
13 0.85 计算古典概型问题的概率
14 0.85 球的表面积的有关计算;多面体与球体内切外接问题
四、解答题
正弦定理边角互化的应用;三角形面积公式及其应用;用和、差角的正弦公式化
15 0.85
简、求值;正弦定理解三角形
由频率分布直方图估计中位数;平均数的和差倍分性质;由频率分布直方图估计
16 0.85
平均数;估计总体的方差、标准差
17 0.65 利用互斥事件的概率公式求概率;计算古典概型问题的概率
18 0.65 锥体体积的有关计算;证明线面平行;证明面面垂直
19 0.65 求点面距离;证明面面垂直;求二面角
知识点分析
序号 知识点 对应题号
1 复数 1
2 平面向量 2,9,12
3 计数原理与概率统计 3,6,13,16,17
4 空间向量与立体几何 4,5,8,11,14,18,19
5 三角函数与解三角形 7,8,10,15
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
同课章节目录
