1.2.2 数轴 课件(共32张PPT)
文档属性
| 名称 | 1.2.2 数轴 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 16:11:04 | ||
图片预览









文档简介
(共32张PPT)
人教版(2024)
七年级上册
1.2.2 数轴
第一章 · 有理数
正数和负数
知识目标
1.清晰阐述数轴的概念。
2.准确说出数轴三要素(原点、正方向、单位长度)的作用。
3.熟练掌握用数轴上的点表示有理数的方法,了解有理数与数轴上的点之间的对应关系。
能力目标
1.通过观察、思考、动手画数轴的过程,培养抽象概括能力和动手操作能力。
2.在探索有理数与数轴上点对应关系的过程中,发展数形结合思维。
素质目标
1.培养严谨的科学态度和良好的数学学习习惯,注重细节。
2.通过对数轴与有理数关系的探究,激发对数学内在美的追求,体会数学中数与形的和谐统一。
教学难点
教学重点
数轴的概念及三要素的理解和掌握;用数轴上的点准确表示有理数
理解数轴三要素的作用;体会有理数与数轴上的点之间的对应关系
情景导入
1
合作探究
2
抽象概括
3
示范讲解
4
课堂练习
5
课堂小结
6
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
同学们,在日常生活中我们经常用这个工具来测量什么?
(1) ℃ (2) ℃
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
你能借助温度计,用一条直线上的点表示我们上一节课学习的有理数吗?
0
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
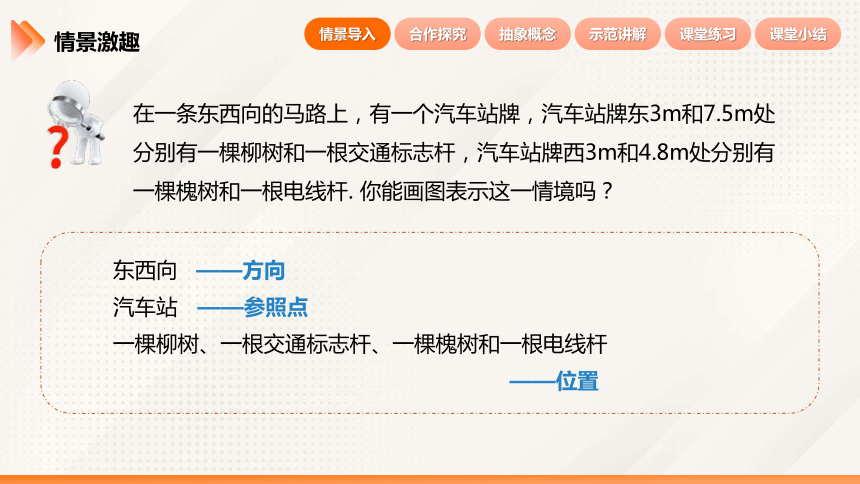
在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处分别有一棵柳树和一根交通标志杆,汽车站牌西3m和4.8m处分别有一棵槐树和一根电线杆. 你能画图表示这一情境吗?
东西向
——方向
汽车站
——参照点
一棵柳树、一根交通标志杆、一棵槐树和一根电线杆
——位置
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
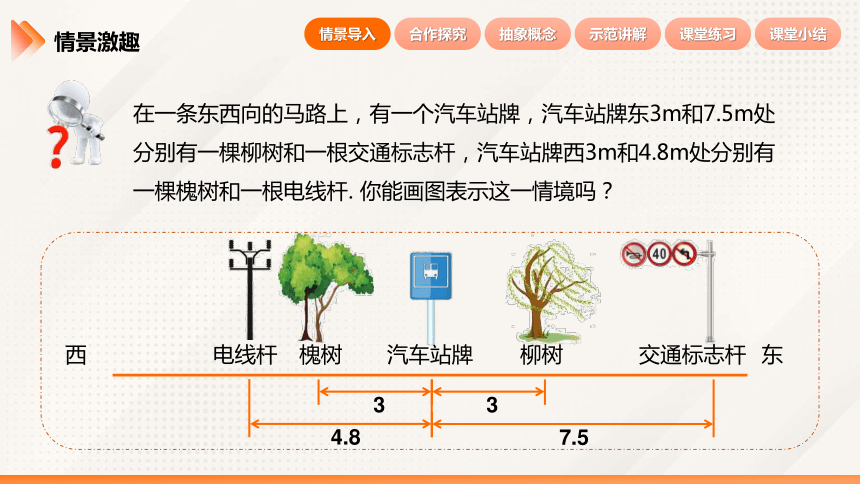
在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处分别有一棵柳树和一根交通标志杆,汽车站牌西3m和4.8m处分别有一棵槐树和一根电线杆. 你能画图表示这一情境吗?
西
东
汽车站牌
3
7.5
柳树
交通标志杆
3
4.8
槐树
电线杆
分析问题,寻找对应
怎样能够简明地表示柳树、交通标志杆、槐树、电线杆与汽车站牌的相对位置关系(方向、距离)?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
“东”与“西”与“正”与“负”一样,是“相反意义的量”.
如果以东为正,在一条直线上任取一点 O 为基准点,规定1个单位长度(线段 OA 的长)代表1m长.
A
1
点0左边,与点0距离3个和4.8个单位长度的点D和点E,分别表示槐树和电线杆的位置.
在点0右边,与点0距离3个和7.5个单位长度的点B和点C,分别表示柳树和杨树的位置;
O
0
分析问题,寻找对应
怎样能够简明地表示柳树、交通标志杆、槐树、电线杆与汽车站牌的相对位置关系(方向、距离)?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
O
B
C
D
E
0
3
7.5
-3
-4.8
A
1
点 O 左边的点表示负数,点 O 右边的点表示正数.
这样,我们就用负数、0、正数表示出了这条直线上的点.
新知探究
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
汽车站牌
柳树
交通标志杆
槐树
电线杆
O
B
C
D
E
0
3
7.5
-3
-4.8
A
1
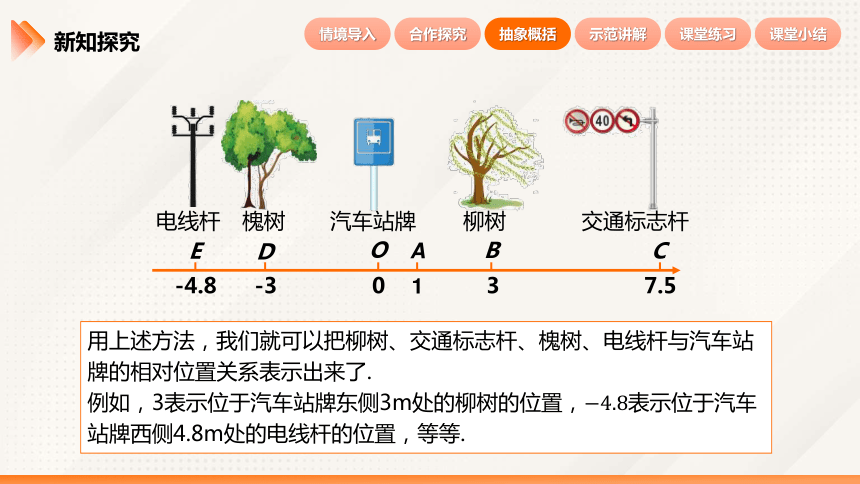
用上述方法,我们就可以把柳树、交通标志杆、槐树、电线杆与汽车站牌的相对位置关系表示出来了.
例如,3表示位于汽车站牌东侧3m处的柳树的位置,表示位于汽车站牌西侧4.8m处的电线杆的位置,等等.
数轴的概念及画法(▲重点)
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
一般地说,在数学中人们用画图的方式把数“直观化”,通常用一条直线上的点表示数,这条直线叫做数轴.
数轴要满足以下要求: (三要素)
(1) 在直线上任取一个点表示数0,这个点叫做原点;
(2) 通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3) 选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法表示-1,-2,-3,….
为了读、画方便,直线画成水平或竖直的
数轴的概念及画法(▲重点)
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
0
1
2
3
4
5
6
7
-1
-2
-3
-4
-5
单位长度
原点
正方向(规定向右)
原点将数轴(原点除外)分成两部分,其中正方向一侧的部分叫作数轴的正半轴;另一侧的部分叫作数轴的负半轴.
像这样,规定了原点、正方向和单位长度的直线叫作数轴.
正半轴上表示的数是正数,负半轴上表示的数是负数.
数轴的概念及画法(▲重点)
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
概念解读
判断下列直线都是数轴吗?说说你的理由.
没有原点,故错误
-2应在-1左边,故错误
没有正方向,故错误
具备数轴的三要素,故正确
有理数与数轴上的点之间的对应关系
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
数轴可以表示整数(如下图),那么数轴怎么来表示分数和小数?
0
1
2
3
4
5
6
7
-1
-2
-3
-4
-5
你会表示出在数轴的正半轴上,距离原点 6.5 个单位长度的点吗?
6.5
有理数与数轴上的点之间的对应关系
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
观察数轴上的有理数排列的大小,你能得出哪些结论?
0
1
2
3
4
5
6
7
-1
-2
-3
-4
-5
① 位于数轴左(下)边的数总比右(上)边的数小.
② 一般地,设a是一个正数,则数轴上表示数 a在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
左
右
a
a
原点的距离是 个单位长度的点有两个,一个在正半轴,一个在负半轴..
0
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
画出数轴,并在数轴上表示下列各数:
例1
解
0
1
2
3
4
-1
-2
-3
-4
.
.
.
.
.
.
.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
下列四个数轴的画法中,规范的是( )
A. B.
C. D.
例2
解
选项A的数轴单位长度不一致,因此选项A不正确,不符合题意;
选项B的数轴无原点,无正方向,因此选项B不正确,不符合题意;
选项C符合数轴的意义,正确,符合题意;
选项D的数轴没有正方向,因此选项D不正确,不符合题意.
C
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
数轴是规定了( )
A.原点和正方向的一条直线 B.单位长度的一条直线
C.原点和单位长度的一条直线
D.原点、正方向和单位长度
例3
解
数轴是规定了原点、正方向和单位长度的一条直线,
D选项符合题意.
D
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1. 如图,写出数轴上点 A,B,C,D,E 表示的数.
0
1
2
3
-1
-2
-3
2.5
A
B
C
D
E
A:0
B:-2
C:1
D:2.5
E:-3
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2. 画出数轴,并在数轴上表示下列有理数:
-1
1
-3
-4
-2
0
-5
5
2
3
4
.
.
.
.
.
.
.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3. 在数轴上,表示 -2 与 4 的点之间(包括这两个点)有_____个点表示的数是整数,它们表示的数分别是 _______________________,其中负整数有_____个.
0
1
2
3
4
-1
-2
7
2
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4. 在数轴上,点 A 表示的数是,从点 A 出发,沿数轴向某一方向移动 4 个单位长度到达点 B,则点 B 表示的数是多少?
-2
-1
0
1
2
3
-3
-4
-5
-6
-7
A
B
B
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
5. 到原点距离为3个单位长度的数是 .
6. 在数轴上点A表示数1,点B与点A相距3个单位,点B表示数是 .
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
7.小明发现一个被墨水污染的数轴如图所示,则被墨迹盖住部分的整数有( )
A.1个 B.2个 C.3个 D.4个
被墨迹盖住部分的整数有,共4个
D
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
8.如图,数轴上点A表示的数可能是( )
A.-2.6 B.-2.01 C.-3.4 D.3.37.
A
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2025·山东·中考)如图,数轴上表示的点是( )
A.M B.N C.P D.Q
【分析】本题主要考查了数轴,弄清数轴上表示数的位置是解题的关键.
观察数轴得到表示的点即可.
【详解】解:如图,在数轴上的点M、N、P、Q中,表示的点是M.
故选:A.
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2024·河南·中考)如图,数轴上点P表示的数是( )
A. B.0 C.1 D.2
【分析】本题考查了数轴,掌握数轴的定义是解题的关键.
根据数轴的定义和特点可知,点P表示的数为,从而求解.
【详解】解:根据题意可知点P表示的数为,
故选:A.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
数轴的概念
绘制数轴;了解有理数与数轴上的点之间的对应关系
了解了数轴的三要素
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1. 数轴的概念:一般地,在数学中人们用画图把数“直观化”.用一条直线上的点表示数,这条直线叫做数轴;
2. 数轴的三要素:原点、正方向、单位长度;
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3. 数与形的关系:有理数与数轴上的点对应的关系;
4. 数学思想:数形结合的思想.
有理数
数轴上的点
(数)
(形)
转
化
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:课本P16复习巩固:第2题;
B层:课本P16综合应用:第6题..
下 课
人教版(2024)
七年级上册
1.2.2 数轴
第一章 · 有理数
正数和负数
知识目标
1.清晰阐述数轴的概念。
2.准确说出数轴三要素(原点、正方向、单位长度)的作用。
3.熟练掌握用数轴上的点表示有理数的方法,了解有理数与数轴上的点之间的对应关系。
能力目标
1.通过观察、思考、动手画数轴的过程,培养抽象概括能力和动手操作能力。
2.在探索有理数与数轴上点对应关系的过程中,发展数形结合思维。
素质目标
1.培养严谨的科学态度和良好的数学学习习惯,注重细节。
2.通过对数轴与有理数关系的探究,激发对数学内在美的追求,体会数学中数与形的和谐统一。
教学难点
教学重点
数轴的概念及三要素的理解和掌握;用数轴上的点准确表示有理数
理解数轴三要素的作用;体会有理数与数轴上的点之间的对应关系
情景导入
1
合作探究
2
抽象概括
3
示范讲解
4
课堂练习
5
课堂小结
6
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
同学们,在日常生活中我们经常用这个工具来测量什么?
(1) ℃ (2) ℃
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
你能借助温度计,用一条直线上的点表示我们上一节课学习的有理数吗?
0
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处分别有一棵柳树和一根交通标志杆,汽车站牌西3m和4.8m处分别有一棵槐树和一根电线杆. 你能画图表示这一情境吗?
东西向
——方向
汽车站
——参照点
一棵柳树、一根交通标志杆、一棵槐树和一根电线杆
——位置
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处分别有一棵柳树和一根交通标志杆,汽车站牌西3m和4.8m处分别有一棵槐树和一根电线杆. 你能画图表示这一情境吗?
西
东
汽车站牌
3
7.5
柳树
交通标志杆
3
4.8
槐树
电线杆
分析问题,寻找对应
怎样能够简明地表示柳树、交通标志杆、槐树、电线杆与汽车站牌的相对位置关系(方向、距离)?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
“东”与“西”与“正”与“负”一样,是“相反意义的量”.
如果以东为正,在一条直线上任取一点 O 为基准点,规定1个单位长度(线段 OA 的长)代表1m长.
A
1
点0左边,与点0距离3个和4.8个单位长度的点D和点E,分别表示槐树和电线杆的位置.
在点0右边,与点0距离3个和7.5个单位长度的点B和点C,分别表示柳树和杨树的位置;
O
0
分析问题,寻找对应
怎样能够简明地表示柳树、交通标志杆、槐树、电线杆与汽车站牌的相对位置关系(方向、距离)?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
O
B
C
D
E
0
3
7.5
-3
-4.8
A
1
点 O 左边的点表示负数,点 O 右边的点表示正数.
这样,我们就用负数、0、正数表示出了这条直线上的点.
新知探究
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
汽车站牌
柳树
交通标志杆
槐树
电线杆
O
B
C
D
E
0
3
7.5
-3
-4.8
A
1
用上述方法,我们就可以把柳树、交通标志杆、槐树、电线杆与汽车站牌的相对位置关系表示出来了.
例如,3表示位于汽车站牌东侧3m处的柳树的位置,表示位于汽车站牌西侧4.8m处的电线杆的位置,等等.
数轴的概念及画法(▲重点)
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
一般地说,在数学中人们用画图的方式把数“直观化”,通常用一条直线上的点表示数,这条直线叫做数轴.
数轴要满足以下要求: (三要素)
(1) 在直线上任取一个点表示数0,这个点叫做原点;
(2) 通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3) 选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法表示-1,-2,-3,….
为了读、画方便,直线画成水平或竖直的
数轴的概念及画法(▲重点)
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
0
1
2
3
4
5
6
7
-1
-2
-3
-4
-5
单位长度
原点
正方向(规定向右)
原点将数轴(原点除外)分成两部分,其中正方向一侧的部分叫作数轴的正半轴;另一侧的部分叫作数轴的负半轴.
像这样,规定了原点、正方向和单位长度的直线叫作数轴.
正半轴上表示的数是正数,负半轴上表示的数是负数.
数轴的概念及画法(▲重点)
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
概念解读
判断下列直线都是数轴吗?说说你的理由.
没有原点,故错误
-2应在-1左边,故错误
没有正方向,故错误
具备数轴的三要素,故正确
有理数与数轴上的点之间的对应关系
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
数轴可以表示整数(如下图),那么数轴怎么来表示分数和小数?
0
1
2
3
4
5
6
7
-1
-2
-3
-4
-5
你会表示出在数轴的正半轴上,距离原点 6.5 个单位长度的点吗?
6.5
有理数与数轴上的点之间的对应关系
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
观察数轴上的有理数排列的大小,你能得出哪些结论?
0
1
2
3
4
5
6
7
-1
-2
-3
-4
-5
① 位于数轴左(下)边的数总比右(上)边的数小.
② 一般地,设a是一个正数,则数轴上表示数 a在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
左
右
a
a
原点的距离是 个单位长度的点有两个,一个在正半轴,一个在负半轴..
0
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
画出数轴,并在数轴上表示下列各数:
例1
解
0
1
2
3
4
-1
-2
-3
-4
.
.
.
.
.
.
.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
下列四个数轴的画法中,规范的是( )
A. B.
C. D.
例2
解
选项A的数轴单位长度不一致,因此选项A不正确,不符合题意;
选项B的数轴无原点,无正方向,因此选项B不正确,不符合题意;
选项C符合数轴的意义,正确,符合题意;
选项D的数轴没有正方向,因此选项D不正确,不符合题意.
C
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
数轴是规定了( )
A.原点和正方向的一条直线 B.单位长度的一条直线
C.原点和单位长度的一条直线
D.原点、正方向和单位长度
例3
解
数轴是规定了原点、正方向和单位长度的一条直线,
D选项符合题意.
D
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1. 如图,写出数轴上点 A,B,C,D,E 表示的数.
0
1
2
3
-1
-2
-3
2.5
A
B
C
D
E
A:0
B:-2
C:1
D:2.5
E:-3
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2. 画出数轴,并在数轴上表示下列有理数:
-1
1
-3
-4
-2
0
-5
5
2
3
4
.
.
.
.
.
.
.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3. 在数轴上,表示 -2 与 4 的点之间(包括这两个点)有_____个点表示的数是整数,它们表示的数分别是 _______________________,其中负整数有_____个.
0
1
2
3
4
-1
-2
7
2
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4. 在数轴上,点 A 表示的数是,从点 A 出发,沿数轴向某一方向移动 4 个单位长度到达点 B,则点 B 表示的数是多少?
-2
-1
0
1
2
3
-3
-4
-5
-6
-7
A
B
B
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
5. 到原点距离为3个单位长度的数是 .
6. 在数轴上点A表示数1,点B与点A相距3个单位,点B表示数是 .
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
7.小明发现一个被墨水污染的数轴如图所示,则被墨迹盖住部分的整数有( )
A.1个 B.2个 C.3个 D.4个
被墨迹盖住部分的整数有,共4个
D
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
8.如图,数轴上点A表示的数可能是( )
A.-2.6 B.-2.01 C.-3.4 D.3.37.
A
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2025·山东·中考)如图,数轴上表示的点是( )
A.M B.N C.P D.Q
【分析】本题主要考查了数轴,弄清数轴上表示数的位置是解题的关键.
观察数轴得到表示的点即可.
【详解】解:如图,在数轴上的点M、N、P、Q中,表示的点是M.
故选:A.
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2024·河南·中考)如图,数轴上点P表示的数是( )
A. B.0 C.1 D.2
【分析】本题考查了数轴,掌握数轴的定义是解题的关键.
根据数轴的定义和特点可知,点P表示的数为,从而求解.
【详解】解:根据题意可知点P表示的数为,
故选:A.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
数轴的概念
绘制数轴;了解有理数与数轴上的点之间的对应关系
了解了数轴的三要素
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1. 数轴的概念:一般地,在数学中人们用画图把数“直观化”.用一条直线上的点表示数,这条直线叫做数轴;
2. 数轴的三要素:原点、正方向、单位长度;
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3. 数与形的关系:有理数与数轴上的点对应的关系;
4. 数学思想:数形结合的思想.
有理数
数轴上的点
(数)
(形)
转
化
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:课本P16复习巩固:第2题;
B层:课本P16综合应用:第6题..
下 课
同课章节目录
