山东省威海市乳山市银滩高级中学2024-2025学年高二下学期期中考试数学试题(PDF版,含解析)
文档属性
| 名称 | 山东省威海市乳山市银滩高级中学2024-2025学年高二下学期期中考试数学试题(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 07:26:47 | ||
图片预览




文档简介
山东省威海市乳山市银滩高级中学 2024-2025 学年
高二下学期期中考试数学试题
一、单选题
1. 函数 的导函数为( )
A. B. C. D.
2. 设随机变量 ,则 ( )
A.0.2 B.0.3 C.0.4 D.0.6
3. 将 4 封不同的信全部投入 3个邮筒,每个邮筒至少投 1封信,则不同投法的
种数为( )
A. B. C.12 D.36
4. 的展开式中含 的项为( )
A. B. C. D.
5. 已知事件 与 独立,且 ,则 ( )
A. B. C. D.
6. 已知函数 的极大值为 1,则 ( )
A. B. C.1 D.3
7. 已知集合 ,集合 ,从 中分别任取三个元
素,两次抽取的结果互不影响,则从 中抽取的三个元素之和不大于 8且从 中
抽取的三个元素之和大于 8的概率为( )
A. B. C. D.
8. 定义在 上的奇函数 的导函数为 ,当 时,恒有
,则不等式 的解集为( )
A. B. C. D.
二、多选题
9. 以下说法正确的有( )
A.若随机变量 服从两点分布, ,则
B.相关系数 与回归系数 的符号(正负)相同
C.在对两个分类变量进行 独立性检验时 ,
如果列联表中所有的数据都扩大为原来的十倍,在相同的检验标准下,再去判断
两变量的关联性时,结论不会发生改变
D.两个随机变量的线性相关程度越强,相关系数的绝对值越接近
10. 已知 的展开式中第五项与第七项的二项式系数相等,则( )
A.展开式的二项式系数和为 B.所有项的系数和为
C.第六项的系数最大 D.展开式中不存在常数项
11. 已知函数 ,则( )
A.当 时, 有两个极值点
B.当 时, 在 处有极值
C.当 时,
D.当 时,曲线 关于点 中心对称
三、填空题
12. 将5名志愿者安排到3个路口进行安全疏导,要求每个路口都有志愿者前往,
且每个志愿者只能去一个路口,则不同的安排方法的种数为______.(用数字作
答)
13. 一个口袋中装有形状大小相同的 6个小球,其中有红球 3个,黄球 2个,绿
球 1个,从中依次有放回的摸出 3个球,则摸出同一种颜色球的概率为________.
14. 已知函数 与 在区间 上的图象有两个公共
点,则实数 m 的取值范围为_______.
四、解答题
15. 已知函数 在点 处的切线斜率为 5.
(1)求实数 m 和 n 的值;
(2)方程 在 有解,求实数 t 的取值范围.
16. 为了研究高二学生每天整理数学错题的情况,学校在高二级部学生中采用随
机抽样的方法抽取了 150 名学生,调查他们平时的数学成绩与整理数学错题情况,
统计数据如下.
数学成绩优秀数学成绩不优秀合计
每天都整理数学错题人数 55 20 75
不是每天都整理数学错题人数30 45 75
合计 85 65 150
(1)依据 列联表判断,能否有 99.9%的把握认为数学成绩优秀与每天整理数
学错题有关?
(2)从调查的不是每天都整理数学错题的学生中,按照数学成绩是否优秀采用分
层随机抽样的方法抽取 10 人.若从这 10 人中随机抽取 2人,记 X 为数学成绩
优秀的人数,求 X 的分布列及数学期望.
参考公式: ,其中 .
参考数据:
0.10 0.05 0.0250.0100.0050.001
k 2.7063.8415.0246.6357.87910.828
17. 已知函数 .
(1)求 的极值;
(2)若 对任意 恒成立,求实数 m 的取值范围.
18. 数学考试中的多选题,每题有 4个选项,其中有 2个或 3个正确答案,全部
选出正确答案得 6分.若正确答案是 2个,只选对 1个得 3分,有选错的得 0
分;若正确答案是 3个,只选对 1个得 2分,只选对 2个得 4分,有选错的得 0
分.若多选题正确答案是 2个的概率为 ,正确答案是 3个的概率为
.某学生对其中一道题完全不会,他随机的进行填涂.
(1)若他只随机选择 1个选项,求他的得分 X 的分布列与数学期望:
(2)若他随机选择 2个选项,求他的得分 Y 的分布列与数学期望:
(3)若 ,该同学随机选择 1个选项还是随机选择 2个选项,能使得分更好?
19. 已知函数 .
(1)设 的图象与 轴的交点为 ,在 点处的切线经过点 ,求此切线
的方程;
(2)在(1)的条件下, 在定义域内恒成立,求 的取值范围;
(3)若 ,求 的取值范围.
山东省威海市乳山市银滩高级中学 2024-2025 学年高二下学期期中考试数学
试题
整体难度:适中
考试范围:函数与导数、计数原理与概率统计
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
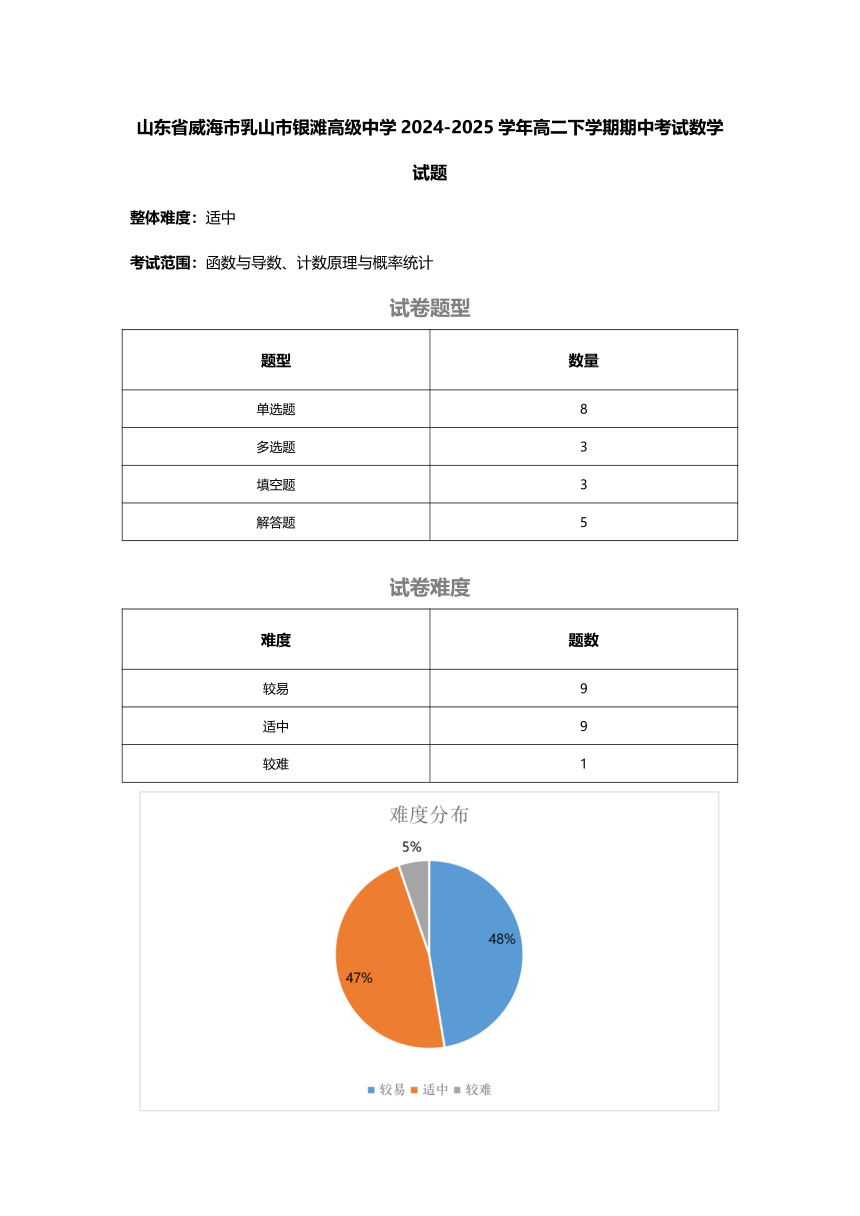
试卷难度
难度 题数
较易 9
适中 9
较难 1
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.85 基本初等函数的导数公式;导数的运算法则
2 0.85 正态曲线的性质;指定区间的概率
3 0.85 分组分配问题;排列组合综合
4 0.65 求二项展开式的第 k 项;三项展开式的系数问题;二项展开式的应用
5 0.85 计算条件概率;独立事件的乘法公式
6 0.65 根据极值求参数
7 0.65 计算古典概型问题的概率;独立事件的乘法公式
用导数判断或证明已知函数的单调性;根据函数的单调性解不等式;函数奇偶性
8 0.65
的应用;导数的运算法则
二、多选题
9 0.85 相关系数的意义及辨析;卡方的计算;二项分布的均值
求二项展开式的第 k 项;二项展开式各项的系数和;二项式的系数和;求指定项
10 0.85
的系数
判断或证明函数的对称性;用导数判断或证明已知函数的单调性;函数极值的辨
11 0.65
析;函数极值点的辨析
三、填空题
12 0.65 分组分配问题
13 0.85 互斥事件的概率加法公式;有放回与无放回问题的概率
根据函数零点的个数求参数范围;函数单调性、极值与最值的综合应用;利用导
14 0.65
数研究函数的零点
四、解答题
15 0.85 已知切线(斜率)求参数;由导数求函数的最值(不含参)
卡方的计算;求离散型随机变量的均值;抽样比、样本总量、各层总数、总体容
16 0.85
量的计算;写出简单离散型随机变量分布列
17 0.65 求已知函数的极值;利用导数研究不等式恒成立问题
18 0.65 写出简单离散型随机变量分布列;求离散型随机变量的均值;均值的实际应用;
利用全概率公式求概率
求在曲线上一点处的切线方程(斜率);利用导数研究不等式恒成立问题;由导
19 0.4
数求函数的最值(含参)
知识点分析
序号 知识点 对应题号
1 函数与导数 1,6,8,11,14,15,17,19
2 计数原理与概率统计 2,3,4,5,7,9,10,12,13,16,18
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
高二下学期期中考试数学试题
一、单选题
1. 函数 的导函数为( )
A. B. C. D.
2. 设随机变量 ,则 ( )
A.0.2 B.0.3 C.0.4 D.0.6
3. 将 4 封不同的信全部投入 3个邮筒,每个邮筒至少投 1封信,则不同投法的
种数为( )
A. B. C.12 D.36
4. 的展开式中含 的项为( )
A. B. C. D.
5. 已知事件 与 独立,且 ,则 ( )
A. B. C. D.
6. 已知函数 的极大值为 1,则 ( )
A. B. C.1 D.3
7. 已知集合 ,集合 ,从 中分别任取三个元
素,两次抽取的结果互不影响,则从 中抽取的三个元素之和不大于 8且从 中
抽取的三个元素之和大于 8的概率为( )
A. B. C. D.
8. 定义在 上的奇函数 的导函数为 ,当 时,恒有
,则不等式 的解集为( )
A. B. C. D.
二、多选题
9. 以下说法正确的有( )
A.若随机变量 服从两点分布, ,则
B.相关系数 与回归系数 的符号(正负)相同
C.在对两个分类变量进行 独立性检验时 ,
如果列联表中所有的数据都扩大为原来的十倍,在相同的检验标准下,再去判断
两变量的关联性时,结论不会发生改变
D.两个随机变量的线性相关程度越强,相关系数的绝对值越接近
10. 已知 的展开式中第五项与第七项的二项式系数相等,则( )
A.展开式的二项式系数和为 B.所有项的系数和为
C.第六项的系数最大 D.展开式中不存在常数项
11. 已知函数 ,则( )
A.当 时, 有两个极值点
B.当 时, 在 处有极值
C.当 时,
D.当 时,曲线 关于点 中心对称
三、填空题
12. 将5名志愿者安排到3个路口进行安全疏导,要求每个路口都有志愿者前往,
且每个志愿者只能去一个路口,则不同的安排方法的种数为______.(用数字作
答)
13. 一个口袋中装有形状大小相同的 6个小球,其中有红球 3个,黄球 2个,绿
球 1个,从中依次有放回的摸出 3个球,则摸出同一种颜色球的概率为________.
14. 已知函数 与 在区间 上的图象有两个公共
点,则实数 m 的取值范围为_______.
四、解答题
15. 已知函数 在点 处的切线斜率为 5.
(1)求实数 m 和 n 的值;
(2)方程 在 有解,求实数 t 的取值范围.
16. 为了研究高二学生每天整理数学错题的情况,学校在高二级部学生中采用随
机抽样的方法抽取了 150 名学生,调查他们平时的数学成绩与整理数学错题情况,
统计数据如下.
数学成绩优秀数学成绩不优秀合计
每天都整理数学错题人数 55 20 75
不是每天都整理数学错题人数30 45 75
合计 85 65 150
(1)依据 列联表判断,能否有 99.9%的把握认为数学成绩优秀与每天整理数
学错题有关?
(2)从调查的不是每天都整理数学错题的学生中,按照数学成绩是否优秀采用分
层随机抽样的方法抽取 10 人.若从这 10 人中随机抽取 2人,记 X 为数学成绩
优秀的人数,求 X 的分布列及数学期望.
参考公式: ,其中 .
参考数据:
0.10 0.05 0.0250.0100.0050.001
k 2.7063.8415.0246.6357.87910.828
17. 已知函数 .
(1)求 的极值;
(2)若 对任意 恒成立,求实数 m 的取值范围.
18. 数学考试中的多选题,每题有 4个选项,其中有 2个或 3个正确答案,全部
选出正确答案得 6分.若正确答案是 2个,只选对 1个得 3分,有选错的得 0
分;若正确答案是 3个,只选对 1个得 2分,只选对 2个得 4分,有选错的得 0
分.若多选题正确答案是 2个的概率为 ,正确答案是 3个的概率为
.某学生对其中一道题完全不会,他随机的进行填涂.
(1)若他只随机选择 1个选项,求他的得分 X 的分布列与数学期望:
(2)若他随机选择 2个选项,求他的得分 Y 的分布列与数学期望:
(3)若 ,该同学随机选择 1个选项还是随机选择 2个选项,能使得分更好?
19. 已知函数 .
(1)设 的图象与 轴的交点为 ,在 点处的切线经过点 ,求此切线
的方程;
(2)在(1)的条件下, 在定义域内恒成立,求 的取值范围;
(3)若 ,求 的取值范围.
山东省威海市乳山市银滩高级中学 2024-2025 学年高二下学期期中考试数学
试题
整体难度:适中
考试范围:函数与导数、计数原理与概率统计
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
较易 9
适中 9
较难 1
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.85 基本初等函数的导数公式;导数的运算法则
2 0.85 正态曲线的性质;指定区间的概率
3 0.85 分组分配问题;排列组合综合
4 0.65 求二项展开式的第 k 项;三项展开式的系数问题;二项展开式的应用
5 0.85 计算条件概率;独立事件的乘法公式
6 0.65 根据极值求参数
7 0.65 计算古典概型问题的概率;独立事件的乘法公式
用导数判断或证明已知函数的单调性;根据函数的单调性解不等式;函数奇偶性
8 0.65
的应用;导数的运算法则
二、多选题
9 0.85 相关系数的意义及辨析;卡方的计算;二项分布的均值
求二项展开式的第 k 项;二项展开式各项的系数和;二项式的系数和;求指定项
10 0.85
的系数
判断或证明函数的对称性;用导数判断或证明已知函数的单调性;函数极值的辨
11 0.65
析;函数极值点的辨析
三、填空题
12 0.65 分组分配问题
13 0.85 互斥事件的概率加法公式;有放回与无放回问题的概率
根据函数零点的个数求参数范围;函数单调性、极值与最值的综合应用;利用导
14 0.65
数研究函数的零点
四、解答题
15 0.85 已知切线(斜率)求参数;由导数求函数的最值(不含参)
卡方的计算;求离散型随机变量的均值;抽样比、样本总量、各层总数、总体容
16 0.85
量的计算;写出简单离散型随机变量分布列
17 0.65 求已知函数的极值;利用导数研究不等式恒成立问题
18 0.65 写出简单离散型随机变量分布列;求离散型随机变量的均值;均值的实际应用;
利用全概率公式求概率
求在曲线上一点处的切线方程(斜率);利用导数研究不等式恒成立问题;由导
19 0.4
数求函数的最值(含参)
知识点分析
序号 知识点 对应题号
1 函数与导数 1,6,8,11,14,15,17,19
2 计数原理与概率统计 2,3,4,5,7,9,10,12,13,16,18
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
同课章节目录
