甘肃省定西市临洮县第二中学2024-2025学年高二下学期期中考试数学试题(PDF版,含解析)
文档属性
| 名称 | 甘肃省定西市临洮县第二中学2024-2025学年高二下学期期中考试数学试题(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 07:30:02 | ||
图片预览




文档简介
甘肃省临洮县第二中学 2024-2025 学年高二下学期
期中考试数学试题
一、单选题
1. 已知函数 ,则 ( )
A.2 B.4 C.3 D.1
2. 若向量 , ,则 ( )
A. B. C. D.
3. 如果函数 的图象如图,那么导函数 的图象可能是( )
B. D.
A. C.
4. 已知函数 的导函数为 ,且满足 ,则
( )
A. B. C.1 D.
5. 已知函数 是奇函数,则曲线 在点 处的
切线方程是
A. B. C. D.
6. 在空间直角坐标系中,已知点 与点 ,若在 轴上有一点
满足 ,则点 坐标为( )
A. B. C. D.
7. 已知函数 ,若 是函数 的唯一极值点,则实数
的取值范围是 ( )
A. B.
C. D.
8. 已知空间直角坐标系 中有一点 ,点 是平面 内的直线
上的动点,则 , 两点间的最短距离是( )
A. C.
B. D.
二、多选题
9. 已知函数 ,则下列结论正确的是( )
A.当 时,函数 的单调递减区间是
B.当 时,单调递增区间是
C.当 时,极小值是
D.若 在 上是增函数,则 的取值范围为
10. (多选题)如图,四边形 ABCD 是边长为 1的正方形,ED⊥平面 ABCD,FB⊥
平面 ABCD,且 ED=FB=1,G 为线段 EC 上的动点,下列结论正确的是( )
A.EC⊥AF
B.该几何体外接球的表面积为 3π
C.若 G 为线段 EC 的中点,则 GB∥平面 AEF
2 2
D.AG +BG 的最小值为 3
三、单选题
11. 定义在 上的函数 ,已知 是它的导函数,且恒有
成立,则有( )
A. B.
C. D.
四、填空题
12. 函数 单调减区间是____________.
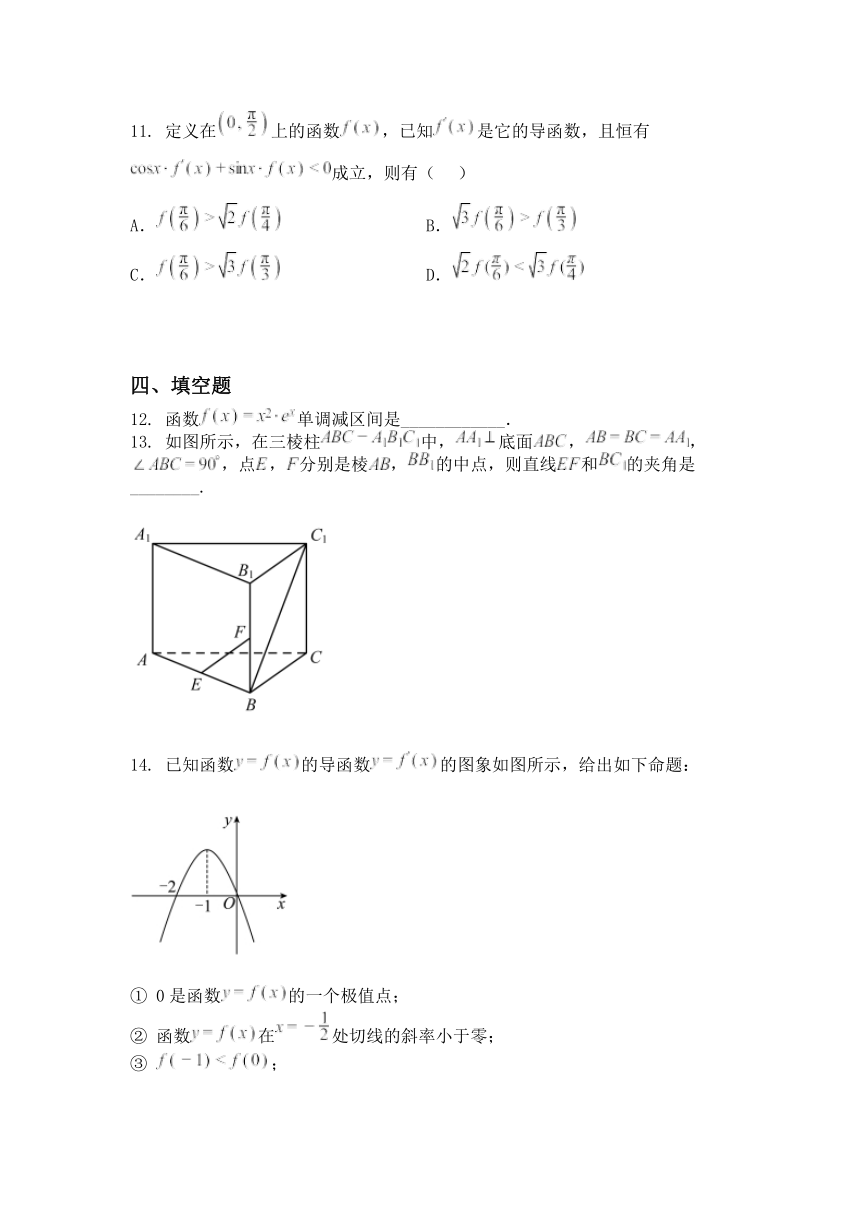
13. 如图所示,在三棱柱 中, 底面 , ,
,点 , 分别是棱 , 的中点,则直线 和 的夹角是
________.
14. 已知函数 的导函数 的图象如图所示,给出如下命题:
① 0是函数 的一个极值点;
② 函数 在 处切线的斜率小于零;
③ ;
④ 当 时, .
其中正确的命题是___________.(写出所有正确命题的序号)
五、解答题
15. 如图,在平行六面体 中, , , ,
, , 是 的中点,设 , ,
.
(1)用 , , 表示 ;
(2)求 的长.
16. 已知函数 .
(1)当 时,求曲线 在 处的切线方程;
(2)若 在区间(0,e]存在极小值,求 a 的取值范围.
17. 已知函数 为自然对数的底数
(1)求 在 处的切线方程;
(2)当 时, ,求实数 的最大值;
(3)证明:当 时, 在 处取极小值.
18. 如图,在四棱锥 中,底面 是矩形, ,
, .以 的中心 为球心, 为直径的球面交 于点 ,交
于点 .
(1)求该球体的体积.
(2)求直线 与平面 所成的角的大小.
(3)求点 到平面 的距离.
19. 已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)当 时,求函数 的单调区间;
(3)当 时, 恒成立,求 的取值范围.
甘肃省临洮县第二中学 2024-2025 学年高二下学期期中考试数学试题
整体难度:适中
考试范围:函数与导数、空间向量与立体几何、平面向量
试卷题型
题型 数量
单选题 9
多选题 2
填空题 3
解答题 5
试卷难度
难度 题数
容易 2
较易 7
适中 6
较难 2
困难 2
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.94 求某点处的导数值;导数的运算法则;简单复合函数的导数
2 0.94 空间向量的坐标运算;空间向量模长的坐标表示
3 0.85 函数与导函数图象之间的关系
4 0.85 求某点处的导数值;导数的运算法则
5 0.85 求在曲线上一点处的切线方程(斜率)
6 0.85 空间距离公式的应用
7 0.15 根据极值点求参数
8 0.65 求二次函数的值域或最值;空间距离公式的应用
用导数判断或证明已知函数的单调性;比较函数值的大小关系;基本初等函数的
11 0.85
导数公式;导数的运算法则
二、多选题
由函数在区间上的单调性求参数;求已知函数的极值;利用导数求函数的单调区
9 0.65
间(不含参)
10 0.65 空间位置关系的向量证明
三、填空题
12 0.85 利用导数求函数的单调区间(不含参)
13 0.65 求异面直线所成的角
函数与导函数图象之间的关系;用导数判断或证明已知函数的单调性;函数(导
14 0.85
函数)图象与极值的关系
四、解答题
15 0.65 向量加法法则的几何应用;已知数量积求模
16 0.4 求在曲线上一点处的切线方程(斜率);根据极值求参数
求在曲线上一点处的切线方程(斜率);求已知函数的极值;函数单调性、极值
17 0.15
与最值的综合应用;利用导数研究函数的零点
线面角的向量求法;点到平面距离的向量求法;球的体积的有关计算;空间向量
18 0.65
的坐标运算
利用导数求函数的单调区间(不含参);利用导数研究不等式恒成立问题;求在
19 0.4
曲线上一点处的切线方程(斜率)
知识点分析
序号 知识点 对应题号
1 函数与导数 1,3,4,5,7,8,9,11,12,14,16,17,19
2 空间向量与立体几何 2,6,8,10,13,18
3 平面向量 15
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
期中考试数学试题
一、单选题
1. 已知函数 ,则 ( )
A.2 B.4 C.3 D.1
2. 若向量 , ,则 ( )
A. B. C. D.
3. 如果函数 的图象如图,那么导函数 的图象可能是( )
B. D.
A. C.
4. 已知函数 的导函数为 ,且满足 ,则
( )
A. B. C.1 D.
5. 已知函数 是奇函数,则曲线 在点 处的
切线方程是
A. B. C. D.
6. 在空间直角坐标系中,已知点 与点 ,若在 轴上有一点
满足 ,则点 坐标为( )
A. B. C. D.
7. 已知函数 ,若 是函数 的唯一极值点,则实数
的取值范围是 ( )
A. B.
C. D.
8. 已知空间直角坐标系 中有一点 ,点 是平面 内的直线
上的动点,则 , 两点间的最短距离是( )
A. C.
B. D.
二、多选题
9. 已知函数 ,则下列结论正确的是( )
A.当 时,函数 的单调递减区间是
B.当 时,单调递增区间是
C.当 时,极小值是
D.若 在 上是增函数,则 的取值范围为
10. (多选题)如图,四边形 ABCD 是边长为 1的正方形,ED⊥平面 ABCD,FB⊥
平面 ABCD,且 ED=FB=1,G 为线段 EC 上的动点,下列结论正确的是( )
A.EC⊥AF
B.该几何体外接球的表面积为 3π
C.若 G 为线段 EC 的中点,则 GB∥平面 AEF
2 2
D.AG +BG 的最小值为 3
三、单选题
11. 定义在 上的函数 ,已知 是它的导函数,且恒有
成立,则有( )
A. B.
C. D.
四、填空题
12. 函数 单调减区间是____________.
13. 如图所示,在三棱柱 中, 底面 , ,
,点 , 分别是棱 , 的中点,则直线 和 的夹角是
________.
14. 已知函数 的导函数 的图象如图所示,给出如下命题:
① 0是函数 的一个极值点;
② 函数 在 处切线的斜率小于零;
③ ;
④ 当 时, .
其中正确的命题是___________.(写出所有正确命题的序号)
五、解答题
15. 如图,在平行六面体 中, , , ,
, , 是 的中点,设 , ,
.
(1)用 , , 表示 ;
(2)求 的长.
16. 已知函数 .
(1)当 时,求曲线 在 处的切线方程;
(2)若 在区间(0,e]存在极小值,求 a 的取值范围.
17. 已知函数 为自然对数的底数
(1)求 在 处的切线方程;
(2)当 时, ,求实数 的最大值;
(3)证明:当 时, 在 处取极小值.
18. 如图,在四棱锥 中,底面 是矩形, ,
, .以 的中心 为球心, 为直径的球面交 于点 ,交
于点 .
(1)求该球体的体积.
(2)求直线 与平面 所成的角的大小.
(3)求点 到平面 的距离.
19. 已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)当 时,求函数 的单调区间;
(3)当 时, 恒成立,求 的取值范围.
甘肃省临洮县第二中学 2024-2025 学年高二下学期期中考试数学试题
整体难度:适中
考试范围:函数与导数、空间向量与立体几何、平面向量
试卷题型
题型 数量
单选题 9
多选题 2
填空题 3
解答题 5
试卷难度
难度 题数
容易 2
较易 7
适中 6
较难 2
困难 2
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.94 求某点处的导数值;导数的运算法则;简单复合函数的导数
2 0.94 空间向量的坐标运算;空间向量模长的坐标表示
3 0.85 函数与导函数图象之间的关系
4 0.85 求某点处的导数值;导数的运算法则
5 0.85 求在曲线上一点处的切线方程(斜率)
6 0.85 空间距离公式的应用
7 0.15 根据极值点求参数
8 0.65 求二次函数的值域或最值;空间距离公式的应用
用导数判断或证明已知函数的单调性;比较函数值的大小关系;基本初等函数的
11 0.85
导数公式;导数的运算法则
二、多选题
由函数在区间上的单调性求参数;求已知函数的极值;利用导数求函数的单调区
9 0.65
间(不含参)
10 0.65 空间位置关系的向量证明
三、填空题
12 0.85 利用导数求函数的单调区间(不含参)
13 0.65 求异面直线所成的角
函数与导函数图象之间的关系;用导数判断或证明已知函数的单调性;函数(导
14 0.85
函数)图象与极值的关系
四、解答题
15 0.65 向量加法法则的几何应用;已知数量积求模
16 0.4 求在曲线上一点处的切线方程(斜率);根据极值求参数
求在曲线上一点处的切线方程(斜率);求已知函数的极值;函数单调性、极值
17 0.15
与最值的综合应用;利用导数研究函数的零点
线面角的向量求法;点到平面距离的向量求法;球的体积的有关计算;空间向量
18 0.65
的坐标运算
利用导数求函数的单调区间(不含参);利用导数研究不等式恒成立问题;求在
19 0.4
曲线上一点处的切线方程(斜率)
知识点分析
序号 知识点 对应题号
1 函数与导数 1,3,4,5,7,8,9,11,12,14,16,17,19
2 空间向量与立体几何 2,6,8,10,13,18
3 平面向量 15
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
同课章节目录
