2.1.2两条直线平行和垂直的判定 课件(共18张PPT)
文档属性
| 名称 | 2.1.2两条直线平行和垂直的判定 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 847.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 14:16:10 | ||
图片预览






文档简介
(共18张PPT)
2.1.2 两条直线平行和垂直的判定
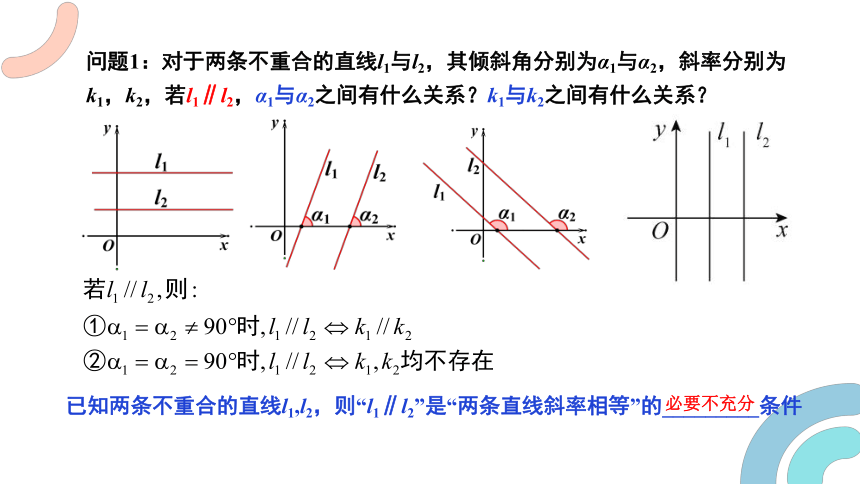
问题1:对于两条不重合的直线l1与l2,其倾斜角分别为α1与α2,斜率分别为k1,k2,若l1∥l2,α1与α2之间有什么关系?k1与k2之间有什么关系?
已知两条不重合的直线l1,l2,则“l1∥l2”是“两条直线斜率相等”的_________条件
必要不充分
1.两条直线平行的判定
对于斜率分别为k1,k2的两条直线l1,l2,
可用斜率相等证三点共线.
练习1.若三点A(2,1),B(﹣2,m),C(6,8)在同一条直线上,则m的值为______.
问题2:对于两条直线l1与l2,其方向向量分别为与,斜率分别为k1,k2,若l1⊥l2,与之间有什么关系?k1与k2之间有什么关系?
2.两条直线垂直的判定
对于斜率分别为k1,k2的两条直线l1,l2,
[例1]已知直线l1过点A(3,a),B(a-2,3),直线l2过点C(2,3),D(﹣1,a-2),
若l1⊥l2,求实数a的值.
2.两条直线垂直的判定
练习2.已知定点A(-1,3),B(4,2),以AB为直径作圆,与x轴有交点P,则交点P的坐标是 .
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)若两条直线平行,则斜率一定相等.( × )
(2)斜率相等的两条直线(不重合)一定平行.( √ )
(3)只有斜率之积为-1的两条直线才垂直.( × )
(4)若两条直线垂直,则斜率乘积为-1.( × )
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
例2.已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线AB与PQ的位置关系,并证明你的结论.
例4.已知A(一6,0),B(3,6),P(0,3),Q(6,—6),试判断直线AB与PQ的位置关系.
例3.已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
例5.已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状.
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
练习3.已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A、B、C、D四点,试判定图形ABCD的形状.
直角梯形
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
练习4.已知矩形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2),则第四个顶点D的坐标为________.
练习5.已知点A(0,3),B(-1,0),C(3,0),且四边形ABCD为直角梯形,求点D的坐标.
题型点拨——用斜率关系判断直线的位置关系或形状
析:kAB=3,kBC=0
则kAB·kBC=0≠-1,即AB与BC不垂直
①由AD//BC,BC⊥CD求D
②由AB//DC,AB⊥AD求D
分类讨论思想
【典例】 已知A(-m-3,2),B(-2m-4,4),C(-m,m),D(3,3m+2)四点,若直线AB⊥CD,求m的值.
【变式训练】 已知A(m-1,2),B(1,1),C(3,m2-m-1)三点,若AB⊥BC,则m的值为 .
与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
【小结】与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
2.1.2 两条直线平行和垂直的判定
问题1:对于两条不重合的直线l1与l2,其倾斜角分别为α1与α2,斜率分别为k1,k2,若l1∥l2,α1与α2之间有什么关系?k1与k2之间有什么关系?
已知两条不重合的直线l1,l2,则“l1∥l2”是“两条直线斜率相等”的_________条件
必要不充分
1.两条直线平行的判定
对于斜率分别为k1,k2的两条直线l1,l2,
可用斜率相等证三点共线.
练习1.若三点A(2,1),B(﹣2,m),C(6,8)在同一条直线上,则m的值为______.
问题2:对于两条直线l1与l2,其方向向量分别为与,斜率分别为k1,k2,若l1⊥l2,与之间有什么关系?k1与k2之间有什么关系?
2.两条直线垂直的判定
对于斜率分别为k1,k2的两条直线l1,l2,
[例1]已知直线l1过点A(3,a),B(a-2,3),直线l2过点C(2,3),D(﹣1,a-2),
若l1⊥l2,求实数a的值.
2.两条直线垂直的判定
练习2.已知定点A(-1,3),B(4,2),以AB为直径作圆,与x轴有交点P,则交点P的坐标是 .
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)若两条直线平行,则斜率一定相等.( × )
(2)斜率相等的两条直线(不重合)一定平行.( √ )
(3)只有斜率之积为-1的两条直线才垂直.( × )
(4)若两条直线垂直,则斜率乘积为-1.( × )
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
例2.已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线AB与PQ的位置关系,并证明你的结论.
例4.已知A(一6,0),B(3,6),P(0,3),Q(6,—6),试判断直线AB与PQ的位置关系.
例3.已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
例5.已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状.
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
练习3.已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A、B、C、D四点,试判定图形ABCD的形状.
直角梯形
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
练习4.已知矩形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2),则第四个顶点D的坐标为________.
练习5.已知点A(0,3),B(-1,0),C(3,0),且四边形ABCD为直角梯形,求点D的坐标.
题型点拨——用斜率关系判断直线的位置关系或形状
析:kAB=3,kBC=0
则kAB·kBC=0≠-1,即AB与BC不垂直
①由AD//BC,BC⊥CD求D
②由AB//DC,AB⊥AD求D
分类讨论思想
【典例】 已知A(-m-3,2),B(-2m-4,4),C(-m,m),D(3,3m+2)四点,若直线AB⊥CD,求m的值.
【变式训练】 已知A(m-1,2),B(1,1),C(3,m2-m-1)三点,若AB⊥BC,则m的值为 .
与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
【小结】与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
