2024-2025学年四川省资阳市高一(下)期末数学试卷(PDF版,含解析)
文档属性
| 名称 | 2024-2025学年四川省资阳市高一(下)期末数学试卷(PDF版,含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 807.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 00:00:00 | ||
图片预览




文档简介
2024-2025学年四川省资阳市高一(下)期末数学试卷
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求。
1.(5分)已知平面向量,.若与共线,则x=( )
A.2 B. C. D.﹣2
2.(5分)已知复数z1=2+i,z2=1﹣2i,复数z=z2+z1,则z的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(5分)一组数1,2,2,2,3,3,3,4,5,6的85%分位数为( )
A.4 B. C.5 D.
4.(5分)函数y=sin2x+cos(2x+π)的最小正周期为( )
A. B.π C.2π D.4π
5.(5分)如图,在△ABC中,点D满足,E为AC的中点,则( )
A. B. C. D.
6.(5分)如图,在四面体ABCD中,若AB=CB,AD=CD,E是AC的中点,则下列结论正确的是( )
A.平面ABC⊥平面ABD B.平面ABD⊥平面BDC
C.平面ABC⊥平面BDE D.平面ABC⊥平面ADC
7.(5分)已知,tanαtanβ=2,则cos(α﹣β)=( )
A. B. C. D.
8.(5分)如图,在三棱锥P﹣ABC中,PA⊥平面ABC,PA=BC=2,∠BAC=30°,则该三棱锥外接球的体积为( )
A. B. C. D.
二、选择题:本大题共3小题,每小题6分,共计18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分。
(多选)9.(6分)某地区举行了足球联赛,联赛结束后的数据显示:甲队每场比赛平均失球数是1.6,各场比赛失球个数的标准差为1.2;乙队每场比赛平均失球数是2.3,各场比赛失球个数的标准差是0.5,下列说法中正确的是( )
A.平均说来甲队比乙队防守技术好
B.甲队在防守中有时表现较差,有时表现又非常好
C.甲队比乙队技术水平更稳定
D.乙队很少不失球
(多选)10.(6分)若向量,满足,,则( )
A.与的夹角为
B.
C.
D.在上的投影向量为
(多选)11.(6分)函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,则下列结论正确的是( )
A.
B.若将f(x)的图象向右平移个单位,则所得函数是奇函数
C.若,,则a的范围为[2,+∞)
D.若函数y=f(x)﹣1的三个相邻零点分别为x1,x2,x3(x1<x2<x3),且|x1﹣x2|=λ|x2﹣x3|,则λ的值是或2
三、填空题:本题共3小题,每小题5分,共15分。
12.(5分)已知复数z(i为虚数单位),则|z|= .
13.(5分)将一个总体分为A,B,C三层,其个体数之比为5:3:2.若A,B,C三层的样本的平均数分别为20,30,40,则总体的平均数为 .
14.(5分)已知点G是△ABC的重心,点M,N分别在AB,AC上,且满足,其中x+y=1.若,则△ANG与△ABC的面积之比为 .
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤。
15.已知函数f(x)=2sinxcosx+cos2x(x∈R).
(1)当x取什么值时,函数f(x)取得最大值?并求出该最大值;
(2)若θ为锐角,且,求tan2θ的值.
16.如图,在四棱锥P﹣ABCD中,AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,BC=2,AB=AD=4,E是线段PA的中点.
(1)求证:BE⊥平面PAD;
(2)求四棱锥P﹣ABCD的体积.
17.为增强职工身体素质,某企业鼓励职工积极参加徒步活动.为了解运动情况,企业工会从该企业职工中随机抽取了100名,统计他们的日均运动步数,并得到如下频率分布直方图:
(1)求图中a的值;
(2)估计该企业职工日均运动步数的平均数;(同一组中的数据用该组区间的中点值为代表)
(3)若该企业恰好有的职工的日均运动步数达到了企业制定的“优秀运动者”达标线,试估计该企业制定的“优秀运动者”达标线.
18.在锐角△ABC中,角A,B,C的对边分别为a,b,c,已知,且.
(1)求角A的大小;
(2)若b=2,求△ABC的面积;
(3)求3b+c的取值范围.
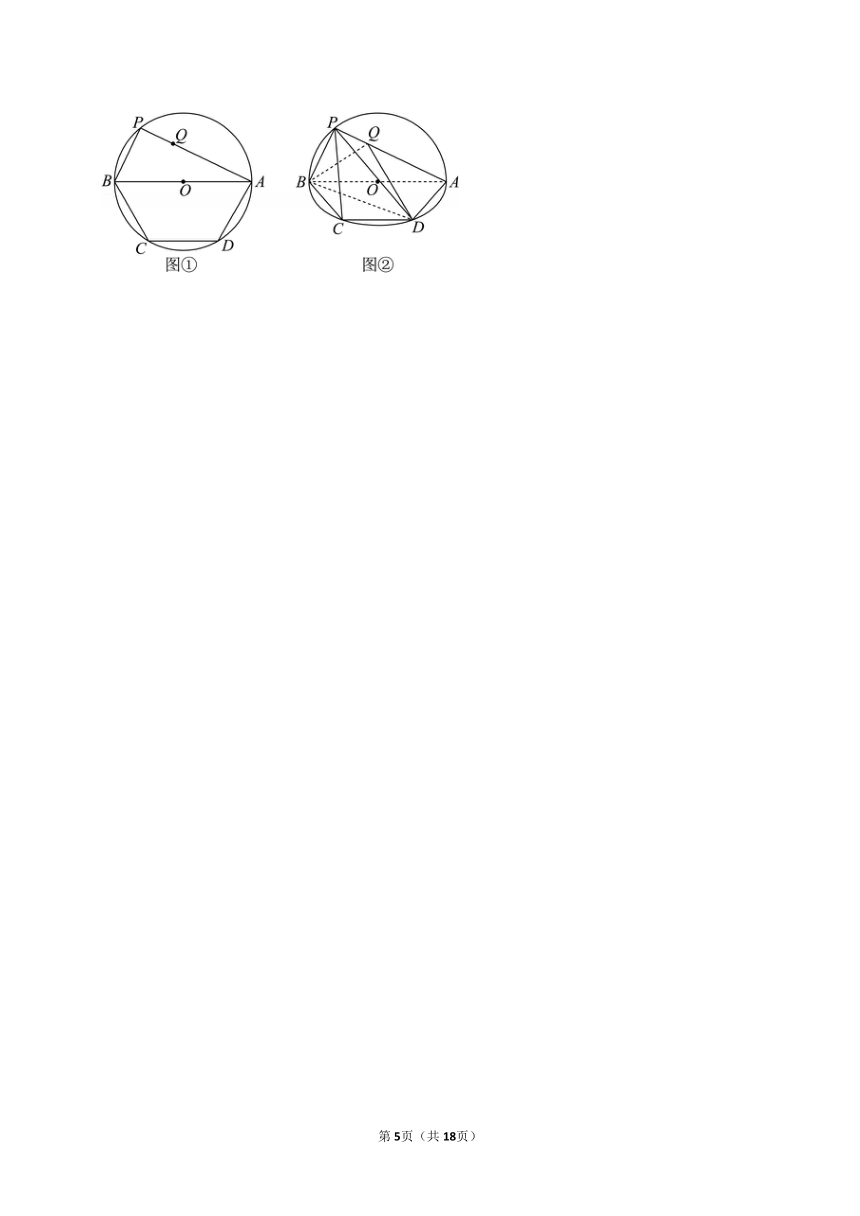
19.如图①,已知等腰梯形ABCD的外接圆圆心O在底边AB上,AB∥CD,CD=AD=3,P是上半圆上的动点(不包含A,B两点),点Q是线段PA上的动点,将半圆APB所在的平面沿直径AB折起,得到图②所示图形,据此解答下列各小题:
(1)当PC∥平面QBD时,求的值;
(2)若PB⊥AD,PB=3,求PA与平面ABCD所成角的正弦值;
(3)若PB≤3,平面PAB⊥平面ABCD,设QB与平面ABCD所成的角为α,二面角Q﹣BD﹣A的平面角为β,求β﹣α取得最大值时tanα的值.
参考答案
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B A C B D C A C
二.多选题(共3小题)
题号 9 10 11
答案 ABD BD ACD
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求。
1.(5分)已知平面向量,.若与共线,则x=( )
A.2 B. C. D.﹣2
【解答】解:平面向量,.与共线,所以.
故选:B.
2.(5分)已知复数z1=2+i,z2=1﹣2i,复数z=z2+z1,则z的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:由复数z1=2+i,z2=1﹣2i,复数z=z2+z1=2+i+1﹣2i=3﹣i,
则,对应的点为(3,1)位于第一象限.
故选:A.
3.(5分)一组数1,2,2,2,3,3,3,4,5,6的85%分位数为( )
A.4 B. C.5 D.
【解答】解:已知一组数1,2,2,2,3,3,3,4,5,6,
又10×0.85=8.5,
所以第85%分位数为从小到大排列的第9个数,即第85%分位数为5.
故选:C.
4.(5分)函数y=sin2x+cos(2x+π)的最小正周期为( )
A. B.π C.2π D.4π
【解答】解:由y=sin2x+cos(2x+π)=sin2x﹣cos2x
(sin2xcoscos2xsin)=2sin(2x),
所以函数的周期为.
故选:B.
5.(5分)如图,在△ABC中,点D满足,E为AC的中点,则( )
A. B. C. D.
【解答】解:因为2,所以,所以.
故选:D.
6.(5分)如图,在四面体ABCD中,若AB=CB,AD=CD,E是AC的中点,则下列结论正确的是( )
A.平面ABC⊥平面ABD B.平面ABD⊥平面BDC
C.平面ABC⊥平面BDE D.平面ABC⊥平面ADC
【解答】解:∵AB=CB,AD=CD,E是AC的中点,则BE⊥AC,DE⊥AC,
∵BE∩DE=E,BE,DE 平面BDE,
∴AC⊥平面BDE,
又AC 平面ABC,∴平面ABC⊥平面BDE,故C正确;
在平面ABC内取点P,作PM⊥AB,PN⊥BE,垂足分别为M,N,如图,
∵平面ABC⊥平面BDE,平面ABC∩平面BDE=BE,
∴PN⊥平面BDE,则有PN⊥BD,
若平面ABC⊥平面ABD,同理可得PM⊥BD,
而PM∩PN=P,PM,PN 平面ABC,
∴BD⊥平面ABC,BD与平面ABC不一定垂直,故A错误;
过A作△ABC边BD上的高AF,连接CF,
由△ABD≌△CBD,得CF是△CBD边BD上的高,
则∠AFC是二面角A﹣BD﹣C的平面角,而∠AFC不一下是直角,
即平面ABD与平面BDC不一定垂直,故B错误;
∵AC⊥平面BE,则∠DEB是二面角D﹣AC﹣B的平面角,∠DEB不一定是直角,
平面ABC与平面ADC不一定垂直,故D错误.
故选:C.
7.(5分)已知,tanαtanβ=2,则cos(α﹣β)=( )
A. B. C. D.
【解答】解:由cos(α+β),可得cosαcosβ﹣sinαsinβ,
因为tanαtanβ2,可得sinαsinβ=2cosαcosβ,
所以,,可得.
故选:A.
8.(5分)如图,在三棱锥P﹣ABC中,PA⊥平面ABC,PA=BC=2,∠BAC=30°,则该三棱锥外接球的体积为( )
A. B. C. D.
【解答】解:在三棱锥P﹣ABC中,设其外接球的球心为点O,△ABC的外接圆的圆心为点E,如图,
连接AO,OE,AE,则OE⊥AE,设△ABC的外接圆的半径为R1,
因为BC=2,∠BAC=30°,
由正弦定理,得 R1=2,即AE=2,
因为PA⊥平面ABC,PA=2,
所以OE=1,
所以三棱锥外接球的半径,
所以三棱锥外接球的体积为.
故选:C.
二、选择题:本大题共3小题,每小题6分,共计18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分。
(多选)9.(6分)某地区举行了足球联赛,联赛结束后的数据显示:甲队每场比赛平均失球数是1.6,各场比赛失球个数的标准差为1.2;乙队每场比赛平均失球数是2.3,各场比赛失球个数的标准差是0.5,下列说法中正确的是( )
A.平均说来甲队比乙队防守技术好
B.甲队在防守中有时表现较差,有时表现又非常好
C.甲队比乙队技术水平更稳定
D.乙队很少不失球
【解答】解:对于A,甲队每场比赛平均失球数是1.6,小于乙队每场比赛平均失球数是2.3,
平均说来甲队比乙队防守技术好,A正确;
对于B,甲队在防守中有时表现较差,有时表现又非常好,B正确;
对于C,甲队各场比赛失球个数的标准差为1.2大于乙队各场比赛失球个数的标准差是0.5,
所以乙队比甲队技术水平更稳定,C错误;
对于D,虽然乙队每场比赛平均失球数是2.3,算是较大的数,而各场比赛失球个数的标准差是0.5,由于标准差很小,方差是0.25更小,说明每场失球数都集中在2.3附近,所以认为乙队很少不失球是正确的,D正确.
故选:ABD.
(多选)10.(6分)若向量,满足,,则( )
A.与的夹角为
B.
C.
D.在上的投影向量为
【解答】解:因为,,
所以,即,
解得,故B正确;
由,
可得,故A错误;
由,
可知与不垂直,故C错误;
因为,
所以在上的投影向量为,故D正确.
故选:BD.
(多选)11.(6分)函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,则下列结论正确的是( )
A.
B.若将f(x)的图象向右平移个单位,则所得函数是奇函数
C.若,,则a的范围为[2,+∞)
D.若函数y=f(x)﹣1的三个相邻零点分别为x1,x2,x3(x1<x2<x3),且|x1﹣x2|=λ|x2﹣x3|,则λ的值是或2
【解答】解:A,,
所以,可得,
又,
因为|φ|<π,所以,
所以,故A正确;
B,将f(x)的图象向右平移个单位后的解析式为,该函数不是奇函数,故B错误;
C,,可得,
,
,
,所以,
所以,所以f(3x)∈[﹣2,1],﹣f(3x)∈[﹣1,2],
所以,所以,故C正确;
D,函数y=f(x)﹣1的零点,即f(x)=1的解,
即,所以,
若,则,此时λ=2,
若,则,此时,所以λ=2或,故D正确.
故选:ACD.
三、填空题:本题共3小题,每小题5分,共15分。
12.(5分)已知复数z(i为虚数单位),则|z|= .
【解答】解:∵z,
∴|z|.
故答案为:.
13.(5分)将一个总体分为A,B,C三层,其个体数之比为5:3:2.若A,B,C三层的样本的平均数分别为20,30,40,则总体的平均数为 27 .
【解答】解:因为A,B,C三层个体数之比为5:3:2,且A,B,C三层的样本的平均数分别为20,30,40,
所以总体的平均数为.
故答案为:27.
14.(5分)已知点G是△ABC的重心,点M,N分别在AB,AC上,且满足,其中x+y=1.若,则△ANG与△ABC的面积之比为 .
【解答】解:根据点G是△ABC的重心,可得,
结合题意,可得,
设,则,
因为,所以,结合x+y=1,解得,,
由,可得,
因为△ABC的重心G到AC的距离等于点B到AC距离的,
所以.
故答案为:.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤。
15.已知函数f(x)=2sinxcosx+cos2x(x∈R).
(1)当x取什么值时,函数f(x)取得最大值?并求出该最大值;
(2)若θ为锐角,且,求tan2θ的值.
【解答】解:(1)由题意得f(x)=sin2x+cos2xsin(2x),
令,解得,
所以当时,f(x)取得最大值,最大值为;
(2)因为,
所以,结合θ为锐角,可得,
所以tanθ,可得.
16.如图,在四棱锥P﹣ABCD中,AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,BC=2,AB=AD=4,E是线段PA的中点.
(1)求证:BE⊥平面PAD;
(2)求四棱锥P﹣ABCD的体积.
【解答】解:(1)证明:因为AD⊥面PAB,BE 面PAB,
因此AD⊥BE,
因为△PAB是等边三角形,E是线段PA的中点,
因此PA⊥BE,
又因为AD∩PA=A,AD,PA 平面PAD,
因此BE⊥平面PAD;
(2)因为AD⊥面PAB,AD 平面ABCD,
因此平面PAB⊥平面ABCD,
又平面PAB∩平面ABCD=AB,
取AB中点为F,
因为△PAB是等边三角形,因此PF⊥AB,
PF 平面PAB,
因此PF⊥平面ABCD,即PF为四棱锥的高,
因为△PAB是等边三角形,AB=4,
因此,
因此四棱锥P﹣ABCD的体积为.
17.为增强职工身体素质,某企业鼓励职工积极参加徒步活动.为了解运动情况,企业工会从该企业职工中随机抽取了100名,统计他们的日均运动步数,并得到如下频率分布直方图:
(1)求图中a的值;
(2)估计该企业职工日均运动步数的平均数;(同一组中的数据用该组区间的中点值为代表)
(3)若该企业恰好有的职工的日均运动步数达到了企业制定的“优秀运动者”达标线,试估计该企业制定的“优秀运动者”达标线.
【解答】解:(1)由频率分布直方图得2(a+0.1+5a+0.12+a)=1,解得a=0.04.
(2)由频率分布直方图可得平均数为:
.
所以该企业职工日均运动步数的平均数约为9.08千步.
(3)日均运动步数在[12,14]的频率为2×0.04=0.08,
日均运动步数在[10,12)的频率为0.12×2=0.24,
日均运动步数在[8,10)的频率为5×0.04×2=0.4,
所以达标线位于[8,10)内,
则达标线为,解得m=9.6,
该企业制定的优秀强国运动者达标线是9.6千步.
18.在锐角△ABC中,角A,B,C的对边分别为a,b,c,已知,且.
(1)求角A的大小;
(2)若b=2,求△ABC的面积;
(3)求3b+c的取值范围.
【解答】解:(1)根据题意可知,,∴,
,
,∵,∴sinB≠0,
∴,∴,
又∵,∴;
(2)在锐角△ABC中,由余弦定理可得a2=b2+c2﹣2bccosA,
又,b=2,,∴,整理得c2﹣2c﹣8=0,
解得c=4或c=﹣2(舍去),∴c=4,
∴;
(3)设锐角△ABC外接圆半径为R,由正弦定理可得:,
∴
,
其中,φ为锐角,
∵△ABC为锐角三角形,则,解得,
∴,
又,
,
∴,即,
∴,从而3b+c的取值范围为.
19.如图①,已知等腰梯形ABCD的外接圆圆心O在底边AB上,AB∥CD,CD=AD=3,P是上半圆上的动点(不包含A,B两点),点Q是线段PA上的动点,将半圆APB所在的平面沿直径AB折起,得到图②所示图形,据此解答下列各小题:
(1)当PC∥平面QBD时,求的值;
(2)若PB⊥AD,PB=3,求PA与平面ABCD所成角的正弦值;
(3)若PB≤3,平面PAB⊥平面ABCD,设QB与平面ABCD所成的角为α,二面角Q﹣BD﹣A的平面角为β,求β﹣α取得最大值时tanα的值.
【解答】解:(1)连接AC交BD于点M,连接QM,
因为CD=AD=3,AB∥CD,所以BC=3,AB=6,
则平面PAC∩平面QBD=QM,
依题意,PC∥平面QBD,PC 平面PAC,
所以PC∥QM,
所以,等腰梯形ABCD中,△MAB∽△MCD,
所以;
(2)因为等腰梯形ABCD的外接圆圆心O在底边AB上,所以∠ADB=90°,
所以AD⊥DB,又因为PB∩BD=B,PB,BD 平面PBD,
所以AD⊥平面PBD,
又AD 平面ABD,所以平面ABD⊥平面PBD,
过P作PN⊥BD于N,连接AN,所以PN⊥平面ABD,
则∠PAN为PA与平面ABCD所成的角,
由(1)可得,
,,
因为PD2+BP2=18+9=27=BD2,所以∠BPD=90°,
所以,
所以,
解得,
所以,
所以PA与平面ABCD所成角的正弦值;
(3)作QH⊥AB于H,连接BQ,
因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
所以QH⊥平面ABCD,所以BH是BQ在平面ABCD内的射影,
因为PB≤3,所以,
所以∠QBH即为QB与平面ABCD所成的角为α∈(0,∠PBA),
则,
过H作GH⊥BD,垂足为G,连结QG,
又因为QH⊥BD,GH∩QH=H,GH,QH 平面QHG,
所以BD⊥平面QHG,
又因为QG 平面QHG,所以BD⊥QG,
所以∠QGH为二面角Q﹣BD﹣A的平面角β,
所以,所以,tanβ=2tanα,
所以,
当且仅当tanα=1时,tan(β﹣α)取得最大值,即β﹣α取得最大值,
所以β﹣α取得最大值时tanα=1.
第1页(共1页)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求。
1.(5分)已知平面向量,.若与共线,则x=( )
A.2 B. C. D.﹣2
2.(5分)已知复数z1=2+i,z2=1﹣2i,复数z=z2+z1,则z的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(5分)一组数1,2,2,2,3,3,3,4,5,6的85%分位数为( )
A.4 B. C.5 D.
4.(5分)函数y=sin2x+cos(2x+π)的最小正周期为( )
A. B.π C.2π D.4π
5.(5分)如图,在△ABC中,点D满足,E为AC的中点,则( )
A. B. C. D.
6.(5分)如图,在四面体ABCD中,若AB=CB,AD=CD,E是AC的中点,则下列结论正确的是( )
A.平面ABC⊥平面ABD B.平面ABD⊥平面BDC
C.平面ABC⊥平面BDE D.平面ABC⊥平面ADC
7.(5分)已知,tanαtanβ=2,则cos(α﹣β)=( )
A. B. C. D.
8.(5分)如图,在三棱锥P﹣ABC中,PA⊥平面ABC,PA=BC=2,∠BAC=30°,则该三棱锥外接球的体积为( )
A. B. C. D.
二、选择题:本大题共3小题,每小题6分,共计18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分。
(多选)9.(6分)某地区举行了足球联赛,联赛结束后的数据显示:甲队每场比赛平均失球数是1.6,各场比赛失球个数的标准差为1.2;乙队每场比赛平均失球数是2.3,各场比赛失球个数的标准差是0.5,下列说法中正确的是( )
A.平均说来甲队比乙队防守技术好
B.甲队在防守中有时表现较差,有时表现又非常好
C.甲队比乙队技术水平更稳定
D.乙队很少不失球
(多选)10.(6分)若向量,满足,,则( )
A.与的夹角为
B.
C.
D.在上的投影向量为
(多选)11.(6分)函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,则下列结论正确的是( )
A.
B.若将f(x)的图象向右平移个单位,则所得函数是奇函数
C.若,,则a的范围为[2,+∞)
D.若函数y=f(x)﹣1的三个相邻零点分别为x1,x2,x3(x1<x2<x3),且|x1﹣x2|=λ|x2﹣x3|,则λ的值是或2
三、填空题:本题共3小题,每小题5分,共15分。
12.(5分)已知复数z(i为虚数单位),则|z|= .
13.(5分)将一个总体分为A,B,C三层,其个体数之比为5:3:2.若A,B,C三层的样本的平均数分别为20,30,40,则总体的平均数为 .
14.(5分)已知点G是△ABC的重心,点M,N分别在AB,AC上,且满足,其中x+y=1.若,则△ANG与△ABC的面积之比为 .
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤。
15.已知函数f(x)=2sinxcosx+cos2x(x∈R).
(1)当x取什么值时,函数f(x)取得最大值?并求出该最大值;
(2)若θ为锐角,且,求tan2θ的值.
16.如图,在四棱锥P﹣ABCD中,AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,BC=2,AB=AD=4,E是线段PA的中点.
(1)求证:BE⊥平面PAD;
(2)求四棱锥P﹣ABCD的体积.
17.为增强职工身体素质,某企业鼓励职工积极参加徒步活动.为了解运动情况,企业工会从该企业职工中随机抽取了100名,统计他们的日均运动步数,并得到如下频率分布直方图:
(1)求图中a的值;
(2)估计该企业职工日均运动步数的平均数;(同一组中的数据用该组区间的中点值为代表)
(3)若该企业恰好有的职工的日均运动步数达到了企业制定的“优秀运动者”达标线,试估计该企业制定的“优秀运动者”达标线.
18.在锐角△ABC中,角A,B,C的对边分别为a,b,c,已知,且.
(1)求角A的大小;
(2)若b=2,求△ABC的面积;
(3)求3b+c的取值范围.
19.如图①,已知等腰梯形ABCD的外接圆圆心O在底边AB上,AB∥CD,CD=AD=3,P是上半圆上的动点(不包含A,B两点),点Q是线段PA上的动点,将半圆APB所在的平面沿直径AB折起,得到图②所示图形,据此解答下列各小题:
(1)当PC∥平面QBD时,求的值;
(2)若PB⊥AD,PB=3,求PA与平面ABCD所成角的正弦值;
(3)若PB≤3,平面PAB⊥平面ABCD,设QB与平面ABCD所成的角为α,二面角Q﹣BD﹣A的平面角为β,求β﹣α取得最大值时tanα的值.
参考答案
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B A C B D C A C
二.多选题(共3小题)
题号 9 10 11
答案 ABD BD ACD
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求。
1.(5分)已知平面向量,.若与共线,则x=( )
A.2 B. C. D.﹣2
【解答】解:平面向量,.与共线,所以.
故选:B.
2.(5分)已知复数z1=2+i,z2=1﹣2i,复数z=z2+z1,则z的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:由复数z1=2+i,z2=1﹣2i,复数z=z2+z1=2+i+1﹣2i=3﹣i,
则,对应的点为(3,1)位于第一象限.
故选:A.
3.(5分)一组数1,2,2,2,3,3,3,4,5,6的85%分位数为( )
A.4 B. C.5 D.
【解答】解:已知一组数1,2,2,2,3,3,3,4,5,6,
又10×0.85=8.5,
所以第85%分位数为从小到大排列的第9个数,即第85%分位数为5.
故选:C.
4.(5分)函数y=sin2x+cos(2x+π)的最小正周期为( )
A. B.π C.2π D.4π
【解答】解:由y=sin2x+cos(2x+π)=sin2x﹣cos2x
(sin2xcoscos2xsin)=2sin(2x),
所以函数的周期为.
故选:B.
5.(5分)如图,在△ABC中,点D满足,E为AC的中点,则( )
A. B. C. D.
【解答】解:因为2,所以,所以.
故选:D.
6.(5分)如图,在四面体ABCD中,若AB=CB,AD=CD,E是AC的中点,则下列结论正确的是( )
A.平面ABC⊥平面ABD B.平面ABD⊥平面BDC
C.平面ABC⊥平面BDE D.平面ABC⊥平面ADC
【解答】解:∵AB=CB,AD=CD,E是AC的中点,则BE⊥AC,DE⊥AC,
∵BE∩DE=E,BE,DE 平面BDE,
∴AC⊥平面BDE,
又AC 平面ABC,∴平面ABC⊥平面BDE,故C正确;
在平面ABC内取点P,作PM⊥AB,PN⊥BE,垂足分别为M,N,如图,
∵平面ABC⊥平面BDE,平面ABC∩平面BDE=BE,
∴PN⊥平面BDE,则有PN⊥BD,
若平面ABC⊥平面ABD,同理可得PM⊥BD,
而PM∩PN=P,PM,PN 平面ABC,
∴BD⊥平面ABC,BD与平面ABC不一定垂直,故A错误;
过A作△ABC边BD上的高AF,连接CF,
由△ABD≌△CBD,得CF是△CBD边BD上的高,
则∠AFC是二面角A﹣BD﹣C的平面角,而∠AFC不一下是直角,
即平面ABD与平面BDC不一定垂直,故B错误;
∵AC⊥平面BE,则∠DEB是二面角D﹣AC﹣B的平面角,∠DEB不一定是直角,
平面ABC与平面ADC不一定垂直,故D错误.
故选:C.
7.(5分)已知,tanαtanβ=2,则cos(α﹣β)=( )
A. B. C. D.
【解答】解:由cos(α+β),可得cosαcosβ﹣sinαsinβ,
因为tanαtanβ2,可得sinαsinβ=2cosαcosβ,
所以,,可得.
故选:A.
8.(5分)如图,在三棱锥P﹣ABC中,PA⊥平面ABC,PA=BC=2,∠BAC=30°,则该三棱锥外接球的体积为( )
A. B. C. D.
【解答】解:在三棱锥P﹣ABC中,设其外接球的球心为点O,△ABC的外接圆的圆心为点E,如图,
连接AO,OE,AE,则OE⊥AE,设△ABC的外接圆的半径为R1,
因为BC=2,∠BAC=30°,
由正弦定理,得 R1=2,即AE=2,
因为PA⊥平面ABC,PA=2,
所以OE=1,
所以三棱锥外接球的半径,
所以三棱锥外接球的体积为.
故选:C.
二、选择题:本大题共3小题,每小题6分,共计18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分。
(多选)9.(6分)某地区举行了足球联赛,联赛结束后的数据显示:甲队每场比赛平均失球数是1.6,各场比赛失球个数的标准差为1.2;乙队每场比赛平均失球数是2.3,各场比赛失球个数的标准差是0.5,下列说法中正确的是( )
A.平均说来甲队比乙队防守技术好
B.甲队在防守中有时表现较差,有时表现又非常好
C.甲队比乙队技术水平更稳定
D.乙队很少不失球
【解答】解:对于A,甲队每场比赛平均失球数是1.6,小于乙队每场比赛平均失球数是2.3,
平均说来甲队比乙队防守技术好,A正确;
对于B,甲队在防守中有时表现较差,有时表现又非常好,B正确;
对于C,甲队各场比赛失球个数的标准差为1.2大于乙队各场比赛失球个数的标准差是0.5,
所以乙队比甲队技术水平更稳定,C错误;
对于D,虽然乙队每场比赛平均失球数是2.3,算是较大的数,而各场比赛失球个数的标准差是0.5,由于标准差很小,方差是0.25更小,说明每场失球数都集中在2.3附近,所以认为乙队很少不失球是正确的,D正确.
故选:ABD.
(多选)10.(6分)若向量,满足,,则( )
A.与的夹角为
B.
C.
D.在上的投影向量为
【解答】解:因为,,
所以,即,
解得,故B正确;
由,
可得,故A错误;
由,
可知与不垂直,故C错误;
因为,
所以在上的投影向量为,故D正确.
故选:BD.
(多选)11.(6分)函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,则下列结论正确的是( )
A.
B.若将f(x)的图象向右平移个单位,则所得函数是奇函数
C.若,,则a的范围为[2,+∞)
D.若函数y=f(x)﹣1的三个相邻零点分别为x1,x2,x3(x1<x2<x3),且|x1﹣x2|=λ|x2﹣x3|,则λ的值是或2
【解答】解:A,,
所以,可得,
又,
因为|φ|<π,所以,
所以,故A正确;
B,将f(x)的图象向右平移个单位后的解析式为,该函数不是奇函数,故B错误;
C,,可得,
,
,
,所以,
所以,所以f(3x)∈[﹣2,1],﹣f(3x)∈[﹣1,2],
所以,所以,故C正确;
D,函数y=f(x)﹣1的零点,即f(x)=1的解,
即,所以,
若,则,此时λ=2,
若,则,此时,所以λ=2或,故D正确.
故选:ACD.
三、填空题:本题共3小题,每小题5分,共15分。
12.(5分)已知复数z(i为虚数单位),则|z|= .
【解答】解:∵z,
∴|z|.
故答案为:.
13.(5分)将一个总体分为A,B,C三层,其个体数之比为5:3:2.若A,B,C三层的样本的平均数分别为20,30,40,则总体的平均数为 27 .
【解答】解:因为A,B,C三层个体数之比为5:3:2,且A,B,C三层的样本的平均数分别为20,30,40,
所以总体的平均数为.
故答案为:27.
14.(5分)已知点G是△ABC的重心,点M,N分别在AB,AC上,且满足,其中x+y=1.若,则△ANG与△ABC的面积之比为 .
【解答】解:根据点G是△ABC的重心,可得,
结合题意,可得,
设,则,
因为,所以,结合x+y=1,解得,,
由,可得,
因为△ABC的重心G到AC的距离等于点B到AC距离的,
所以.
故答案为:.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤。
15.已知函数f(x)=2sinxcosx+cos2x(x∈R).
(1)当x取什么值时,函数f(x)取得最大值?并求出该最大值;
(2)若θ为锐角,且,求tan2θ的值.
【解答】解:(1)由题意得f(x)=sin2x+cos2xsin(2x),
令,解得,
所以当时,f(x)取得最大值,最大值为;
(2)因为,
所以,结合θ为锐角,可得,
所以tanθ,可得.
16.如图,在四棱锥P﹣ABCD中,AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,BC=2,AB=AD=4,E是线段PA的中点.
(1)求证:BE⊥平面PAD;
(2)求四棱锥P﹣ABCD的体积.
【解答】解:(1)证明:因为AD⊥面PAB,BE 面PAB,
因此AD⊥BE,
因为△PAB是等边三角形,E是线段PA的中点,
因此PA⊥BE,
又因为AD∩PA=A,AD,PA 平面PAD,
因此BE⊥平面PAD;
(2)因为AD⊥面PAB,AD 平面ABCD,
因此平面PAB⊥平面ABCD,
又平面PAB∩平面ABCD=AB,
取AB中点为F,
因为△PAB是等边三角形,因此PF⊥AB,
PF 平面PAB,
因此PF⊥平面ABCD,即PF为四棱锥的高,
因为△PAB是等边三角形,AB=4,
因此,
因此四棱锥P﹣ABCD的体积为.
17.为增强职工身体素质,某企业鼓励职工积极参加徒步活动.为了解运动情况,企业工会从该企业职工中随机抽取了100名,统计他们的日均运动步数,并得到如下频率分布直方图:
(1)求图中a的值;
(2)估计该企业职工日均运动步数的平均数;(同一组中的数据用该组区间的中点值为代表)
(3)若该企业恰好有的职工的日均运动步数达到了企业制定的“优秀运动者”达标线,试估计该企业制定的“优秀运动者”达标线.
【解答】解:(1)由频率分布直方图得2(a+0.1+5a+0.12+a)=1,解得a=0.04.
(2)由频率分布直方图可得平均数为:
.
所以该企业职工日均运动步数的平均数约为9.08千步.
(3)日均运动步数在[12,14]的频率为2×0.04=0.08,
日均运动步数在[10,12)的频率为0.12×2=0.24,
日均运动步数在[8,10)的频率为5×0.04×2=0.4,
所以达标线位于[8,10)内,
则达标线为,解得m=9.6,
该企业制定的优秀强国运动者达标线是9.6千步.
18.在锐角△ABC中,角A,B,C的对边分别为a,b,c,已知,且.
(1)求角A的大小;
(2)若b=2,求△ABC的面积;
(3)求3b+c的取值范围.
【解答】解:(1)根据题意可知,,∴,
,
,∵,∴sinB≠0,
∴,∴,
又∵,∴;
(2)在锐角△ABC中,由余弦定理可得a2=b2+c2﹣2bccosA,
又,b=2,,∴,整理得c2﹣2c﹣8=0,
解得c=4或c=﹣2(舍去),∴c=4,
∴;
(3)设锐角△ABC外接圆半径为R,由正弦定理可得:,
∴
,
其中,φ为锐角,
∵△ABC为锐角三角形,则,解得,
∴,
又,
,
∴,即,
∴,从而3b+c的取值范围为.
19.如图①,已知等腰梯形ABCD的外接圆圆心O在底边AB上,AB∥CD,CD=AD=3,P是上半圆上的动点(不包含A,B两点),点Q是线段PA上的动点,将半圆APB所在的平面沿直径AB折起,得到图②所示图形,据此解答下列各小题:
(1)当PC∥平面QBD时,求的值;
(2)若PB⊥AD,PB=3,求PA与平面ABCD所成角的正弦值;
(3)若PB≤3,平面PAB⊥平面ABCD,设QB与平面ABCD所成的角为α,二面角Q﹣BD﹣A的平面角为β,求β﹣α取得最大值时tanα的值.
【解答】解:(1)连接AC交BD于点M,连接QM,
因为CD=AD=3,AB∥CD,所以BC=3,AB=6,
则平面PAC∩平面QBD=QM,
依题意,PC∥平面QBD,PC 平面PAC,
所以PC∥QM,
所以,等腰梯形ABCD中,△MAB∽△MCD,
所以;
(2)因为等腰梯形ABCD的外接圆圆心O在底边AB上,所以∠ADB=90°,
所以AD⊥DB,又因为PB∩BD=B,PB,BD 平面PBD,
所以AD⊥平面PBD,
又AD 平面ABD,所以平面ABD⊥平面PBD,
过P作PN⊥BD于N,连接AN,所以PN⊥平面ABD,
则∠PAN为PA与平面ABCD所成的角,
由(1)可得,
,,
因为PD2+BP2=18+9=27=BD2,所以∠BPD=90°,
所以,
所以,
解得,
所以,
所以PA与平面ABCD所成角的正弦值;
(3)作QH⊥AB于H,连接BQ,
因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
所以QH⊥平面ABCD,所以BH是BQ在平面ABCD内的射影,
因为PB≤3,所以,
所以∠QBH即为QB与平面ABCD所成的角为α∈(0,∠PBA),
则,
过H作GH⊥BD,垂足为G,连结QG,
又因为QH⊥BD,GH∩QH=H,GH,QH 平面QHG,
所以BD⊥平面QHG,
又因为QG 平面QHG,所以BD⊥QG,
所以∠QGH为二面角Q﹣BD﹣A的平面角β,
所以,所以,tanβ=2tanα,
所以,
当且仅当tanα=1时,tan(β﹣α)取得最大值,即β﹣α取得最大值,
所以β﹣α取得最大值时tanα=1.
第1页(共1页)
同课章节目录
