2.2.1直线的点斜式方程 课件(共18张PPT)
文档属性
| 名称 | 2.2.1直线的点斜式方程 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 16:39:47 | ||
图片预览




文档简介
(共18张PPT)
2.2.1直线的点斜式方程
法国的数学家笛卡尔(1596—1650)是解析几何的创始人之一,他的中心思想是使代数和几何结合起来,他设想,把任何数学问题化为一个代数问题,在把任何代数问题归结到去解一个方程式。
解析几何是数学中最基本的学科之一,也是科学技术中最基本的数学工具之一,解析几何的产生,可说是数学发展史上的一次飞跃。
直线的方程是我们学习解析几何的第一个内容,本节课,我们将在直角坐标系中,通过直线的几何要素,探究直线的方程。
解析几何与笛卡尔
图片欣赏
跨海大桥
图片欣赏
天空之桥
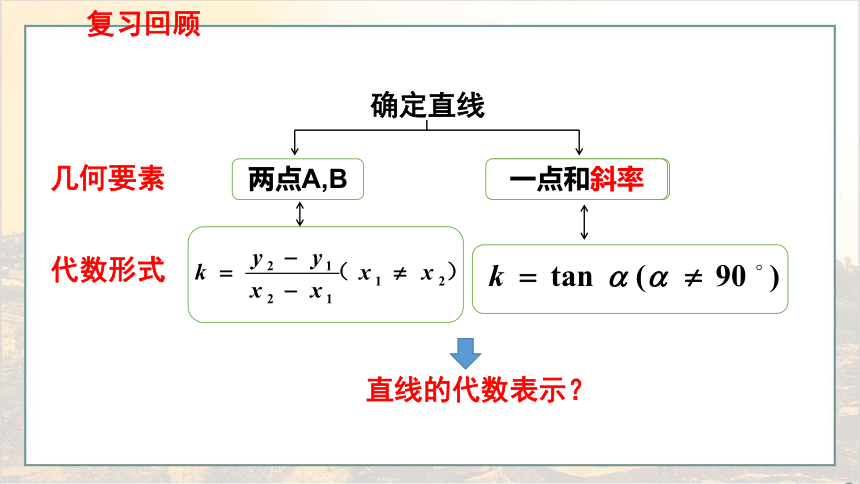
复习回顾
几何要素
代数形式
确定直线
两点A,B
一点和倾斜角
直线的代数表示?
一点和斜率
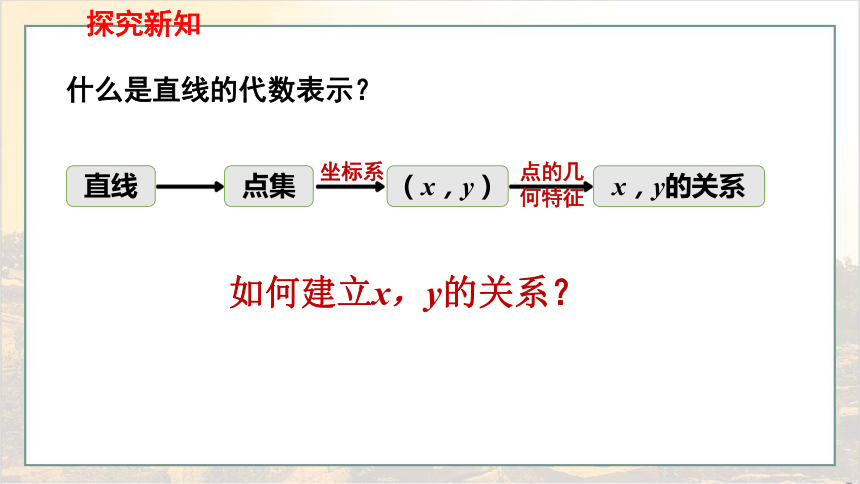
什么是直线的代数表示?
x,y的关系
点的几何特征
直线
点集
坐标系
(x,y)
探究新知
如何建立x,y的关系?
. P0(x0,y0)
. P(x, y)
l
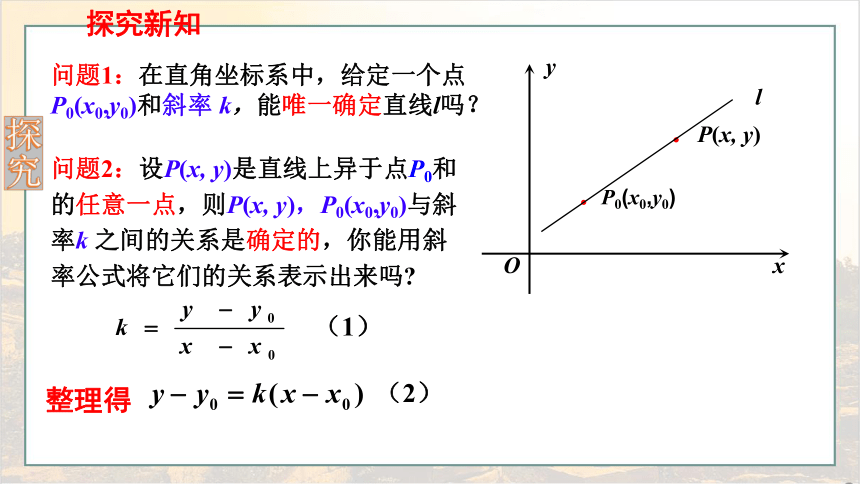
问题1:在直角坐标系中,给定一个点P0(x0,y0)和斜率 k,能唯一确定直线l吗?
探究新知
问题2:设P(x, y)是直线上异于点P0和的任意一点,则P(x, y),P0(x0,y0)与斜率k 之间的关系是确定的,你能用斜率公式将它们的关系表示出来吗
探究
(1)
整理得
(2)
O
x
y
(1)
(2)
问题3:代数式(1)(2)有什么区别 为什么要整理成
探究新知
任意点P(x, y)能代表这条直线上的所有点吗?
直线l上每一个点的坐标(x,y)满足关系式y-y0=k(x-x0)
. P0(x0,y0)
. P(x, y)
l
O
x
y
点P0(x0,y0)不满足式(1)
直线上所有点P(x, y)都满足式(2)
追问:坐标满足关系式y-y0=k(x-x0)的所有点是否都在直线l上?
探究新知
(1) 直线l上每一个点的坐标(x,y)满足关系式y-y0=k(x-x0)
(2)坐标满足关系式y-y0=k(x-x0)的所有点(x,y)都在直线l上
探究新知
小结
整理得
. P0(x0,y0)
l
O
x
y
. P(x, y)
(1) 直线l上每一个点的坐标(x,y)满足关系式y-y0=k(x-x0)
(2)坐标满足关系式y-y0=k(x-x0)的所有点(x,y)都在直线l上
1建系
2设点
3代数关系式
4化简
5验证
1. 写出下列直线的点斜式方程:
(1)经过点A(3,-1),斜率是 ;
(2)经过点B( ,2),倾斜角是30° ;
(3)经过点C(0,3),倾斜角是0° ;
(4)经过点D(-4,-2),倾斜角是90°.
课堂练习1
思考 点斜式方程适用于所有的直线吗?
1.当直线l经过点 ,且倾斜角为90°时,
直线l方程是:
O
x
y
l
2.当直线l经过点 ,且倾斜角为0°时,
直线l方程是:
O
x
y
l
斜率不存在时不适用
斜率为0时适用
1. 写出下列直线的点斜式方程:
(1)经过点A(3,-1),斜率是 ;
(2)经过点B( ,2),倾斜角是30° ;
(3)经过点C(0,3),倾斜角是0° ;
(4)经过点D(-4,-2),倾斜角是90°.
课堂练习1
O
x
y
1
1
2
3
4
P0
P1
学以致用
(1)已知直线的点斜式方是 ,那么此直线的斜率是__________,倾斜角是____________.
(2)已知直线的点斜式方程是 ,那么此直线的斜率是_______,倾斜角是__________.
1
(3) x轴所在直线的方程为_________.
(4) y轴所在直线的方程为_________.
课堂练习2
(5)过点(0,b),斜率为k的直线的方程为_________.
1.直线的点斜式方程:
x
y
O
l
P0
2. x轴所在直线的方程是: y=0 y轴所在直线的方程是: x=0
课堂总结
知识内容
思想方法:
方程思想 类比 一般到特殊
作业布置
一、必做题:
1、预习作业:直线斜截式方程的内容
2、上交作业:教科书P67第1题(1)(2)小题
二、拓展题:
1、查阅解析几何的相关资料,了解解析几何在数学发展史上的地位与作用
2、试用推导直线方程的方法推导圆的方程或解决点的轨迹问题
2.2.1直线的点斜式方程
法国的数学家笛卡尔(1596—1650)是解析几何的创始人之一,他的中心思想是使代数和几何结合起来,他设想,把任何数学问题化为一个代数问题,在把任何代数问题归结到去解一个方程式。
解析几何是数学中最基本的学科之一,也是科学技术中最基本的数学工具之一,解析几何的产生,可说是数学发展史上的一次飞跃。
直线的方程是我们学习解析几何的第一个内容,本节课,我们将在直角坐标系中,通过直线的几何要素,探究直线的方程。
解析几何与笛卡尔
图片欣赏
跨海大桥
图片欣赏
天空之桥
复习回顾
几何要素
代数形式
确定直线
两点A,B
一点和倾斜角
直线的代数表示?
一点和斜率
什么是直线的代数表示?
x,y的关系
点的几何特征
直线
点集
坐标系
(x,y)
探究新知
如何建立x,y的关系?
. P0(x0,y0)
. P(x, y)
l
问题1:在直角坐标系中,给定一个点P0(x0,y0)和斜率 k,能唯一确定直线l吗?
探究新知
问题2:设P(x, y)是直线上异于点P0和的任意一点,则P(x, y),P0(x0,y0)与斜率k 之间的关系是确定的,你能用斜率公式将它们的关系表示出来吗
探究
(1)
整理得
(2)
O
x
y
(1)
(2)
问题3:代数式(1)(2)有什么区别 为什么要整理成
探究新知
任意点P(x, y)能代表这条直线上的所有点吗?
直线l上每一个点的坐标(x,y)满足关系式y-y0=k(x-x0)
. P0(x0,y0)
. P(x, y)
l
O
x
y
点P0(x0,y0)不满足式(1)
直线上所有点P(x, y)都满足式(2)
追问:坐标满足关系式y-y0=k(x-x0)的所有点是否都在直线l上?
探究新知
(1) 直线l上每一个点的坐标(x,y)满足关系式y-y0=k(x-x0)
(2)坐标满足关系式y-y0=k(x-x0)的所有点(x,y)都在直线l上
探究新知
小结
整理得
. P0(x0,y0)
l
O
x
y
. P(x, y)
(1) 直线l上每一个点的坐标(x,y)满足关系式y-y0=k(x-x0)
(2)坐标满足关系式y-y0=k(x-x0)的所有点(x,y)都在直线l上
1建系
2设点
3代数关系式
4化简
5验证
1. 写出下列直线的点斜式方程:
(1)经过点A(3,-1),斜率是 ;
(2)经过点B( ,2),倾斜角是30° ;
(3)经过点C(0,3),倾斜角是0° ;
(4)经过点D(-4,-2),倾斜角是90°.
课堂练习1
思考 点斜式方程适用于所有的直线吗?
1.当直线l经过点 ,且倾斜角为90°时,
直线l方程是:
O
x
y
l
2.当直线l经过点 ,且倾斜角为0°时,
直线l方程是:
O
x
y
l
斜率不存在时不适用
斜率为0时适用
1. 写出下列直线的点斜式方程:
(1)经过点A(3,-1),斜率是 ;
(2)经过点B( ,2),倾斜角是30° ;
(3)经过点C(0,3),倾斜角是0° ;
(4)经过点D(-4,-2),倾斜角是90°.
课堂练习1
O
x
y
1
1
2
3
4
P0
P1
学以致用
(1)已知直线的点斜式方是 ,那么此直线的斜率是__________,倾斜角是____________.
(2)已知直线的点斜式方程是 ,那么此直线的斜率是_______,倾斜角是__________.
1
(3) x轴所在直线的方程为_________.
(4) y轴所在直线的方程为_________.
课堂练习2
(5)过点(0,b),斜率为k的直线的方程为_________.
1.直线的点斜式方程:
x
y
O
l
P0
2. x轴所在直线的方程是: y=0 y轴所在直线的方程是: x=0
课堂总结
知识内容
思想方法:
方程思想 类比 一般到特殊
作业布置
一、必做题:
1、预习作业:直线斜截式方程的内容
2、上交作业:教科书P67第1题(1)(2)小题
二、拓展题:
1、查阅解析几何的相关资料,了解解析几何在数学发展史上的地位与作用
2、试用推导直线方程的方法推导圆的方程或解决点的轨迹问题
