2.3.2两点间的距离公式 课件(共15张PPT)
文档属性
| 名称 | 2.3.2两点间的距离公式 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 16:41:59 | ||
图片预览






文档简介
(共15张PPT)
第二章 直线和圆的方程
2.3.2 两点间的距离公式
*在各种几何量中,最基本的几何量:直线段的长度;
*在解析几何中,最基本的公式:计算直线段的长度即两点间距离的公式.
学习目标
1.通过自主探究,利用向量模长推导两点间距离公式;通过合作互助,利用构造直角三角形推导两点间距离公式,并进行比较。培养逻辑推理、数学运算素养。
3.通过用“坐标法”证明平行四边形的勾股定理,将几何问题代数化,归纳出解决平面几何问题的基本步骤,明确建系的本质,体会数形结合的思想方法.
2.通过例题与练习,达到对两点间距离公式的初步应用。
知识点一:
两点间距离公式的推导与内容
O
y
x
P1
P2
平面向量知识
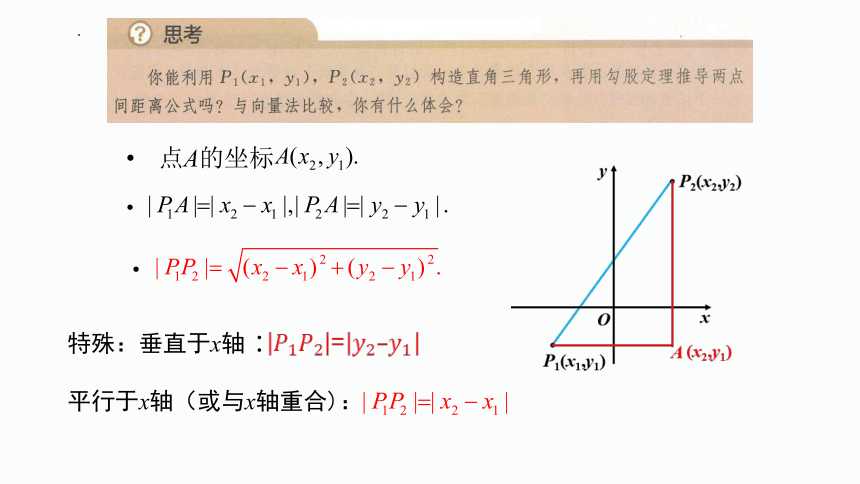
由此得到P1(x1,y1), P2(x2,y2)两点间的距离公式
||=
点A的坐标
特殊:垂直于x轴:
平行于x轴(或与x轴重合):
||=
推导方法:向量法;几何法
内容:
特殊:垂直于x轴:
平行于x轴(或与x轴重合):
||=
知识点一:两点间距离公式的推导与内容
||=
知识点二:
两点间距离公式的简单应用
重点关注:
1、点的引入:尽可能少的变量
2、点的书写:横纵坐标不要颠倒
3、距离的计算:别忘了开方
知识点三:
通过用“坐标法”证明平行四边形的勾股定理,归纳出解决平面几何问题的基本步骤
应用公式,解决问题
例4:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
【追问1】平行四边形的4个点是否需要设出8个不同的参数呢?如何建立平面直角坐标系使得未知量尽量少且不失一般性呢?
【追问2】建立直角坐标系解决问题,比较不同建系方法的优劣.
解:如图建系,
设,,则根据平行四边形的性质,得.
,,,.
所以,=,
.
所以,.
知识点三: “坐标法”解决平面几何问题的基本步骤
第一步
建立适当的坐标系,用坐标表示有关的量
第二步
进行有关代数运算
第三步
把代数运算的结果“翻译”成几何结论
建系的原则主要有两点:
①让尽可能多的点落在坐标轴上,这样便于运算.
②如果条件中有互相垂直的两条线,要考虑将它们作为坐标轴;如果图形为中心对称图形,可考虑将中心作为原点;如果有轴对称性,可考虑将对称轴作为坐标轴.
我们曾用向量法证明过这个结论(必修二第六章),比较“坐标法”和“向量法”,并谈一下体会。
1.取为基底;
2.用表示两条对角线向量,计算所求量间的关系;
3.运算结果“翻译”成几何结论.
*用坐标法解决这个问题的基本步骤与向量法完全类似。
小结提升
知识点一: 两点间距离公式的推导与内容
知识点二:两点间距离公式的简单应用
知识点三:平行四边形勾股定理证明与 “坐标法”解决平面几何问题的基本步骤
谢谢观看
第二章 直线和圆的方程
2.3.2 两点间的距离公式
*在各种几何量中,最基本的几何量:直线段的长度;
*在解析几何中,最基本的公式:计算直线段的长度即两点间距离的公式.
学习目标
1.通过自主探究,利用向量模长推导两点间距离公式;通过合作互助,利用构造直角三角形推导两点间距离公式,并进行比较。培养逻辑推理、数学运算素养。
3.通过用“坐标法”证明平行四边形的勾股定理,将几何问题代数化,归纳出解决平面几何问题的基本步骤,明确建系的本质,体会数形结合的思想方法.
2.通过例题与练习,达到对两点间距离公式的初步应用。
知识点一:
两点间距离公式的推导与内容
O
y
x
P1
P2
平面向量知识
由此得到P1(x1,y1), P2(x2,y2)两点间的距离公式
||=
点A的坐标
特殊:垂直于x轴:
平行于x轴(或与x轴重合):
||=
推导方法:向量法;几何法
内容:
特殊:垂直于x轴:
平行于x轴(或与x轴重合):
||=
知识点一:两点间距离公式的推导与内容
||=
知识点二:
两点间距离公式的简单应用
重点关注:
1、点的引入:尽可能少的变量
2、点的书写:横纵坐标不要颠倒
3、距离的计算:别忘了开方
知识点三:
通过用“坐标法”证明平行四边形的勾股定理,归纳出解决平面几何问题的基本步骤
应用公式,解决问题
例4:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
【追问1】平行四边形的4个点是否需要设出8个不同的参数呢?如何建立平面直角坐标系使得未知量尽量少且不失一般性呢?
【追问2】建立直角坐标系解决问题,比较不同建系方法的优劣.
解:如图建系,
设,,则根据平行四边形的性质,得.
,,,.
所以,=,
.
所以,.
知识点三: “坐标法”解决平面几何问题的基本步骤
第一步
建立适当的坐标系,用坐标表示有关的量
第二步
进行有关代数运算
第三步
把代数运算的结果“翻译”成几何结论
建系的原则主要有两点:
①让尽可能多的点落在坐标轴上,这样便于运算.
②如果条件中有互相垂直的两条线,要考虑将它们作为坐标轴;如果图形为中心对称图形,可考虑将中心作为原点;如果有轴对称性,可考虑将对称轴作为坐标轴.
我们曾用向量法证明过这个结论(必修二第六章),比较“坐标法”和“向量法”,并谈一下体会。
1.取为基底;
2.用表示两条对角线向量,计算所求量间的关系;
3.运算结果“翻译”成几何结论.
*用坐标法解决这个问题的基本步骤与向量法完全类似。
小结提升
知识点一: 两点间距离公式的推导与内容
知识点二:两点间距离公式的简单应用
知识点三:平行四边形勾股定理证明与 “坐标法”解决平面几何问题的基本步骤
谢谢观看
