四年级暑假新课预习提升练第八单元检测卷《垂线和平行线》(含解析)-2024-2025学年度下学期数学 苏教版
文档属性
| 名称 | 四年级暑假新课预习提升练第八单元检测卷《垂线和平行线》(含解析)-2024-2025学年度下学期数学 苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 439.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 19:25:12 | ||
图片预览




文档简介
四年级暑假新课预习提升练第八单元检测卷《垂线和平行线》(含解析)-2024-2025学年度下学期数学苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.从到,分针旋转了( )。
A. B. C. D.
2.下面哪句话正确的?( )
A.如图这样测量跳远成绩,是因为点到直线的距离最短。
B.观察一个长方体纸箱,一次最多能看到4个面。
C.把一条长8厘米的线段向一边延长100厘米后,就成了一条射线。
3.下面说法正确的是( )。
A.把一条线段向一端延长100米,就得到一条射线
B.下午3时30分,钟面上分钟和时针所夹的角是直角
C.810÷5=(810×2)÷(5×2)
D.2升雪碧的容量比2000毫升可乐的容量少
4.下面的图形中,平行线组数最多的是( )。
A. B. C. D.
5.如下图,一张长方形纸折起一个角,已知∠1=25°,∠2=∠3,∠2=( )°。
A.25° B.30° C.45° D.65°
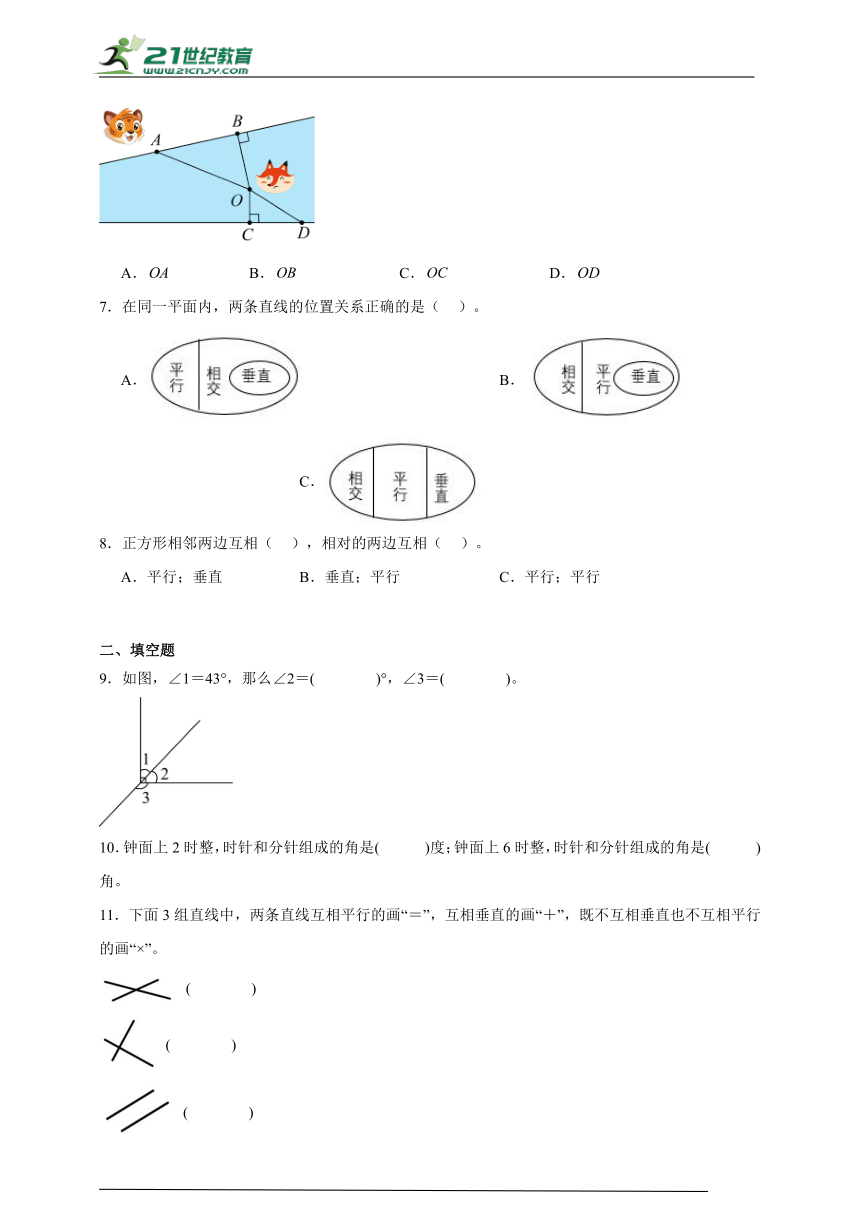
6.如图,一只老虎追赶一只狐狸,狐狸慌不择路掉进了河里。狐狸想尽快上岸,又不能被老虎抓住。聪明的狐狸怎么逃生呢?它会选择下面( )线路。
A. B. C. D.
7.在同一平面内,两条直线的位置关系正确的是( )。
A. B. C.
8.正方形相邻两边互相( ),相对的两边互相( )。
A.平行;垂直 B.垂直;平行 C.平行;平行
二、填空题
9.如图,∠1=43°,那么∠2=( )°,∠3=( )。
10.钟面上2时整,时针和分针组成的角是( )度;钟面上6时整,时针和分针组成的角是( )角。
11.下面3组直线中,两条直线互相平行的画“=”,互相垂直的画“+”,既不互相垂直也不互相平行的画“×”。
( )
( )
( )
12.将一张长方形纸按如图所示的方式折叠。如果,那么( )°。
13.5分=( )秒 240分=( )时
8000毫升=( )升 1平角=( )直角
14.2021年3月,教育部发布了《关于进一步加强中小学生睡眠管理工作的通知》,要求小学生每天睡眠至少应达到9小时。张桦晚上8:45睡觉,第二天早上6:45起床,这时钟面上的时针和分针成( )角,时针转动了( )度。
15.下面的图形都是由一副三角尺拼成的,拼出的每个角是什么角?各是多少度?
角, °。
角, °。
16.把线段的两端都无限延长,就得到一条( )。( )和( )都是无限长的。把一个长方形纸对折再对折,两条折痕互相( )。
三、判断题
17.用10倍的放大镜看6°的角就会变成60°。( )
18.将一个正方形对折两次,折痕可能互相垂直,也可能互相平行。( )
19.射线可以向一端无限延伸,所以无法量出射线的长度。( )
20.平角等于180度,小于180度的角是钝角。( )
21.a和b是两条互相平行的直线,直线a和c平行,所以直线b和c也平行。( )
22.在同一平面内,两条直线的位置关系有相交和垂直。( )
四、计算题
23.根据图中信息计算各角的度数。
计算∠1、∠2、∠3的度数。
24.脱式计算。
8×15+340÷68 246÷[96÷(856-840)]
五、作图题
25.经过点A画出已知直线的平行线,经过点B画出已知直线的垂线。
六、解答题
26.按要求画一画:过点O画直线L的垂线,并量出点O到直线L的距离。点O到直线L的距离是( )厘米。
27.在下面的直线上画出两个点,使这两点之间的距离是4厘米。
想一想,线段和直线有什么关系?
28.长方形纸的一个角折叠后如下图,已知∠1=28°,求∠2的度数。
29.做一做,说一说。
用一个图钉把一张硬纸条钉在木板上,硬纸条可以转动吗?过一点可以画出多少条直线?
30.下图中一个是长方形,一个是正方形,求∠1和∠2的度数。
《四年级暑假新课预习提升练第八单元检测卷《垂线和平行线》(含解析)-2024-2025学年度下学期数学苏教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 C A C B D C A B
1.C
【分析】钟面上共有12大格,围成一个周角,因此每个大格的度数是360°÷12=30°;从8:30到9:00,钟表上的分针从“6”走到了“12”,走了6个大格,因此分针旋转的度数是30°×6,据此即可解答.
【详解】30°×6=180°
从到,分针旋转了180°。
故答案为:C
【点睛】解答此题的关键是明确每个大格的度数是30°。
2.A
【分析】(1)为数学知识的应用,由实际出发,测量跳远成绩的依据是垂线段最短,即测量后脚印与起跳线间的垂直距离即为跳远成绩;
(2)观察一个长方体时,当眼睛在长方体的一个顶点时,能看到的面最多,最多只有3个面;
(3)线段有2个端点,不能向两端无限延伸,能测量长度;直线没有端点,可以向两端无限延伸,不能测量长度;射线有1个端点,可以向一端无限延伸,不能测量长度。
【详解】A.如上图这样测量跳远成绩,是因为点到直线的距离最短,原题说法正确;
B.观察一个长方体纸箱,一次最多能看到3个面,原题说法错误;
C.把一条长8厘米的线段向一边延长100厘米后,还是一条线段,原题说法错误。
故答案为:A
【点睛】此题涉及的知识点较多,但都比较简单,属于基础题,只要认真,容易完成,注意平时基础知识的积累。
3.C
【分析】A选项射线有一个端点,另一端可以无限延伸,射线本身就是无限长的,不能说向一端延长一定长度后得到射线。由此解答。
B选项先找出下午3时30分钟面上时针和分针所在的位置,再进行解答。
C选项根据商不变规律,被除数和除数同时乘或除以相同的数(0 除外),商不变。由此解答。
D选项根据1升=1000毫升,换算后进行解答。
【详解】A.把一条线段向一端延长100米,就得到一条射线,射线不可度量;原题说法错误;
B.下午3时30分,钟面上分针和时针所夹的角是直角,如果时针在3上,分针在6上,钟面上分针和时针所夹的角是直角,但下午3时30分,分针在6上,时针在3和4之间,所以应小于90°;原题说法错误;
C.根据商不变性质,810÷5=(810×2)÷(5×2),说法正确;
D.1升=1000毫升,因此2升=2000毫升。2升雪碧的容量和2000毫升可乐的容量一样;原题说法错误;
故答案为:C
4.B
【分析】同一平面内,不相交的两条直线互相平行;垂直于同一条直线的两直线平行,据此逐项判断。
【详解】A.没有平行线;
B.有3组平行线;
C.有2组平行线;
D.有1组平行线;
故答案为:B
【点睛】要找平行线,就是找不相交的两条线段。
5.D
【分析】1平角是180°,根据图示可知,∠1+∠1+∠2+∠2=180°,因此用180°减去2个∠1后,再除以2即可,依此计算。
【详解】180°-25°-25°=130°
130°÷2=65°
即∠2=65°。
故答案为:D
6.C
【分析】狐狸要想不被老虎抓住,不能逃向老虎所在的岸边,应向对岸逃去。只有OC和OD可以选择。从直线外一点到这条直线所画的垂直线段的长度,叫做点到直线的距离。垂直线段最短。据此可以解答。
【详解】由分析知,OC这条垂线就是狐狸的逃生路线。
故答案为:C
7.A
【分析】在同一平面内的两条不重合的直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况。
【详解】由分析得:
在同一平面内,两条直线的位置关系正确的是。
故答案为:A
【点睛】本题考查同一平面内两条直线的位置关系,注意垂直只是相交的特殊情况。
8.B
【分析】根据长方形的特征,对边平行且相等,4个角都是直角,可知,长方形相邻的两条边互相垂直,相对的两边互相平行。
【详解】根据分析可知:
正方形相邻两边互相垂直,相对的两边互相平行。
故答案为:B
【点睛】此题主要考查长方形的特征以及平行、垂直的定义,应熟练掌握。
9. 47 133°
【分析】观察上图,∠1和∠2拼成一个直角,用90°-∠1,求出∠2;∠3和∠2拼成一个平角,用180°-∠2,求出∠3,据此解答。
【详解】90°-43°=47°,则∠2=47°;
180°-47°=133°,则∠3=133°。
10. 60 平
【分析】钟面上有12个大格,1个大格的所对的夹角的度数是30度,2时,分针指向12,时针指向2,所以时针与分针的夹角是2个大格,用乘法即可解答;
6时整,时针指向6,分针指向12,中间6格,据此即可解答。
【详解】360÷12=30(度),30×2=60(度),因此钟面上2时整,时针和分针组成的角是60度。
30×6=180(度),钟面上6时整,时针和分针组成的角是180度,也就是平角。
11. × + =
【分析】在同一个平面内,不相交的两条直线叫做平行线;两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直。既不互相平行也不互相垂直的两条直线就相交。据此解答即可。
【详解】(×)
(+)
(=)
【点睛】此题考查了垂直与平行的特征和性质,要熟练掌握。
12.30
【分析】观察上图可知:2个∠1和1个∠2组成一个平角,用180°减去2个75°,即可求出∠2的度数。
【详解】180°-2×75°
=180°-150°
=30°
∠2=30°。
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角),以及它与各角之间的关系,利用已知角,求出未知角。
13. 300 4 8 2
【分析】1分=60秒,60分=1时,1000毫升=1升,由高级单位化低级单位乘进率,由低级单位化高级单位除以进率;1平角=180°,1直角=90°,据此计算1平角等于多少直角。
【详解】5分=300秒 240分=4时
8000毫升=8升 1平角=2直角
【点睛】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
14. 锐 300
【分析】6:45时分针指向9,时针指向6和7之间,这时时针和分针所成的角小于90°,所以这时钟面上的时针和分针成锐角;从晚上8:45到次日6:45共10小时。每小时转30°,10小时转动 10×30°=300°。
【详解】6:45时分针指向9,时针指向6和7之间,这时钟面上的时针和分针成锐角;
晚上12:45-晚上8:45=4(小时)
次日6:45-凌晨0:45=6(小时)
4+6=10(小时)
10×30°=300°
时针转动了300度。
15. 锐 75 钝 150
【分析】大于0°小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角;
一副三角尺有90°、45°、45°,90°、60°、30°几个角,分别从每个三角尺中任取一个角,进行加或减,拼出不同的角;据此计算角的度数,再根据角的分类解题即可。
【详解】30°+45°=75°
锐角,75°。
60°+90°=150°
钝角,150°。
16. 直线 直线 射线 平行或垂直
【分析】线段有两个端点,长度有限可以测量长度;射线只有一个端点,可以向一端无限延长,长度无限无法测量长度;直线没有端点,可以向两端无限延长,长度无限无法测量长度;
在同一平面内不相交的两条直线互相平行,在同一平面内相交成直角的两条直线互相垂直;把长方形对折再对折,如果两次对折的方向相同,则两条折痕不会相交,即互相平行,如果两次对折的方向不同,即一次沿长对折,一次沿宽对折,则两条折痕会相交成直角,即互相垂直。据此解答。
【详解】根据分析可知:
把线段的两端都无限延长,就得到一条直线。直线和射线都是无限长的。把一个长方形纸对折再对折,两条折痕互相平行或垂直。
17.×
【分析】用放大镜看物体,只是改变了看到物体的视角,即改变了眼睛看到物体的大小,但是物体的形状并不会改变,看角也是一样的,角的形状是不变的,即角两边叉开的大小是不变的,所以原来是6°的角经过放大后还是6°的角,据此判断即可。
【详解】用10倍的放大镜看6°的角放大后还是6°的角,并不会变成60°的角。
故答案为:×
18.√
【分析】同一平面内,两条直线相交成直角,这两条直线互相垂直;同一平面内,永不相交的两条直线叫做平行线,组成平行线的两条直线互相平行;依此画图并判断。
【详解】画图如下:
由此可知,把一个正方形纸对折两次,两条折痕可能互相垂直,也可能互相平行。原题表述正确。
故答案为:√
19.√
【分析】根据直线、射线和线段的含义:直线没有端点,可以向两端无限延伸,不能量出长度;射线只有一个端点,只能向一端无限延伸,不能量出长度;线段有两个端点,不能向两端延伸,可以量出长度;据此解答即可。
【详解】射线只有一个端点,可以向一端无限延伸,因此无法测量其长度,因为长度是有限的,而射线是无限的,所以无法用具体的数值表示射线的长度;故原题说法正确。
故答案为:√
20.×
【分析】锐角:大于0度小于90度的角;钝角:大于90度小于180度的角;直角:等于90度的角;平角:等于180度的角;周角:等于360度的角;据此解答即可。
【详解】平角等于180度,大于90度小于180度的角是钝角;
小于180度的角是钝角,说法错误,因为锐角、直角、钝角都小于180度;所以原题说法错误。
故答案为:×
21.√
【分析】在同一平面内,如果两条直线都和第三条直线平行,则这两条直线也相互平行。
【详解】因在同一平面内,直线a和直线b相互平行,直线a和直线c相互平行,直线b和c都和直线a平行,所以直线b和直线c相互平行。原题说法正确。
故答案为:√
22.×
【分析】在同一平面内的两条不重合的直线,只有两种位置关系,即相交或平行,而垂直是相交的一种特殊情况。据此分析作答。
【详解】在同一平面内,两条直线永远不相交的情况即为平行,两条直线交于一点的情况即为相交,当两条直线交于一点且夹角为90度即为垂直,所以垂直为相交的一种特殊情况,所以在同一平面内,两条直线的位置关系有相交和平行。
故答案为:×
23.∠1的度数是60°;∠2的度数是30°;∠3的度数是60°
【分析】根据题图可知,先根据∠1+30°=90°求出∠1的度数,∠1和∠2组成的角也是直角,等于90°,据此计算出∠2的度数;∠3和∠2组成的角也是直角,等于90°,据此计算出∠3的度数;据此解答。
【详解】根据分析可得:
∠1+30°=90°,所以∠1=90°-30°=60°
∠2=90°-∠1=90°-60°=30°
∠3=90°-∠2=90°-30°=60°
∠1的度数是60°;∠2的度数是30°;∠3的度数是60°。
24.125;41
【分析】根据混合运算计算法则:
(1)先计算乘除,再计算加法;
(2)先计算小括号里的减法,再计算中括号里的除法,最后计算中括号外的除法。
【详解】8×15+340÷68
=120+5
=125
246÷[96÷(856-840)]
=246÷[96÷16]
=246÷6
=41
25.见详解
【分析】过直线外一点作已知直线的平行线的方法:先把三角尺的一条直角边与已知直线重合;再用直尺紧靠着三角尺的另一条直角边。固定直尺,然后沿着直尺平移三角尺,使直线外的点在三角尺上。沿直角边画出另一条直线即可;过直线上或直线外一点作垂线的方法:先把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上。再沿三角尺的另一条直角边画一条直线,并画上垂直符号。这条直线就是已知直线的垂线。
【详解】
如图:
26.画图见详解;4
【分析】过直线上或直线外一点作垂线:先把三角尺的一条直角边与已知直线重合,然后将三角尺沿着直线移动,使得直线上或直线外的已知点在三角尺的另一条直角边上,最后沿三角尺的另一条直角边画一条直线,并画上直角符号,这条直线就是已知直线的垂线。然后用尺子量出垂线段的长度就是所求距离。
【详解】
点O到直线L的距离是4厘米。
【点睛】本题考查了过直线外一点作垂线的方法,点到直线的垂线段的长度就是点到直线的距离。
27.见详解
【分析】先用直尺的边与这条直线重合,在直尺的0刻度线处点上一点,再在4厘米处点上另外一点,这两点间的距离就是4厘米;
线段有两个端点,有限长,能用直尺测量出长度;直线没有端点,可以向两边无限延长,无法测量长度;据此解答即可。
【详解】作图如下:
线段和直线的关系:在直线上点上不同的两点,这两点之间的一段叫做线段;把线段的两端无限延长,就能得到一条直线。
28.34°
【分析】
如图,长方形纸的一个角折叠,使∠1=∠3,观察图可以发现,∠1、∠2和∠3这个三角组成直角,直角为90°,用90°依次减去∠1和∠3,即可求出∠2的度数,据此解答即可。
【详解】90°-28°-28°
=62°-28°
=34°
答:∠2的度数为34°。
29.可以;无数条
【分析】在平面上,过一点可以画无数条直线,不能确定一条直线;只有过两点才能确定一条直线,据此解答。
【详解】用一个图钉把一张硬纸条钉在木板上,硬纸条可以转动,过一点可以画无数条直线。
30.45°;45°
【分析】长方形和正方形的四个角都是直角,直角是90°。长方形的长刚好把正方形平均分成两个三角形。所以中间共用的角是45°,据此可以算出∠1和∠2的度数。
【详解】∠1=90°-45°=45°
∠2=90°-45°=45°
答:∠1是45°,∠2也是45°。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.从到,分针旋转了( )。
A. B. C. D.
2.下面哪句话正确的?( )
A.如图这样测量跳远成绩,是因为点到直线的距离最短。
B.观察一个长方体纸箱,一次最多能看到4个面。
C.把一条长8厘米的线段向一边延长100厘米后,就成了一条射线。
3.下面说法正确的是( )。
A.把一条线段向一端延长100米,就得到一条射线
B.下午3时30分,钟面上分钟和时针所夹的角是直角
C.810÷5=(810×2)÷(5×2)
D.2升雪碧的容量比2000毫升可乐的容量少
4.下面的图形中,平行线组数最多的是( )。
A. B. C. D.
5.如下图,一张长方形纸折起一个角,已知∠1=25°,∠2=∠3,∠2=( )°。
A.25° B.30° C.45° D.65°
6.如图,一只老虎追赶一只狐狸,狐狸慌不择路掉进了河里。狐狸想尽快上岸,又不能被老虎抓住。聪明的狐狸怎么逃生呢?它会选择下面( )线路。
A. B. C. D.
7.在同一平面内,两条直线的位置关系正确的是( )。
A. B. C.
8.正方形相邻两边互相( ),相对的两边互相( )。
A.平行;垂直 B.垂直;平行 C.平行;平行
二、填空题
9.如图,∠1=43°,那么∠2=( )°,∠3=( )。
10.钟面上2时整,时针和分针组成的角是( )度;钟面上6时整,时针和分针组成的角是( )角。
11.下面3组直线中,两条直线互相平行的画“=”,互相垂直的画“+”,既不互相垂直也不互相平行的画“×”。
( )
( )
( )
12.将一张长方形纸按如图所示的方式折叠。如果,那么( )°。
13.5分=( )秒 240分=( )时
8000毫升=( )升 1平角=( )直角
14.2021年3月,教育部发布了《关于进一步加强中小学生睡眠管理工作的通知》,要求小学生每天睡眠至少应达到9小时。张桦晚上8:45睡觉,第二天早上6:45起床,这时钟面上的时针和分针成( )角,时针转动了( )度。
15.下面的图形都是由一副三角尺拼成的,拼出的每个角是什么角?各是多少度?
角, °。
角, °。
16.把线段的两端都无限延长,就得到一条( )。( )和( )都是无限长的。把一个长方形纸对折再对折,两条折痕互相( )。
三、判断题
17.用10倍的放大镜看6°的角就会变成60°。( )
18.将一个正方形对折两次,折痕可能互相垂直,也可能互相平行。( )
19.射线可以向一端无限延伸,所以无法量出射线的长度。( )
20.平角等于180度,小于180度的角是钝角。( )
21.a和b是两条互相平行的直线,直线a和c平行,所以直线b和c也平行。( )
22.在同一平面内,两条直线的位置关系有相交和垂直。( )
四、计算题
23.根据图中信息计算各角的度数。
计算∠1、∠2、∠3的度数。
24.脱式计算。
8×15+340÷68 246÷[96÷(856-840)]
五、作图题
25.经过点A画出已知直线的平行线,经过点B画出已知直线的垂线。
六、解答题
26.按要求画一画:过点O画直线L的垂线,并量出点O到直线L的距离。点O到直线L的距离是( )厘米。
27.在下面的直线上画出两个点,使这两点之间的距离是4厘米。
想一想,线段和直线有什么关系?
28.长方形纸的一个角折叠后如下图,已知∠1=28°,求∠2的度数。
29.做一做,说一说。
用一个图钉把一张硬纸条钉在木板上,硬纸条可以转动吗?过一点可以画出多少条直线?
30.下图中一个是长方形,一个是正方形,求∠1和∠2的度数。
《四年级暑假新课预习提升练第八单元检测卷《垂线和平行线》(含解析)-2024-2025学年度下学期数学苏教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 C A C B D C A B
1.C
【分析】钟面上共有12大格,围成一个周角,因此每个大格的度数是360°÷12=30°;从8:30到9:00,钟表上的分针从“6”走到了“12”,走了6个大格,因此分针旋转的度数是30°×6,据此即可解答.
【详解】30°×6=180°
从到,分针旋转了180°。
故答案为:C
【点睛】解答此题的关键是明确每个大格的度数是30°。
2.A
【分析】(1)为数学知识的应用,由实际出发,测量跳远成绩的依据是垂线段最短,即测量后脚印与起跳线间的垂直距离即为跳远成绩;
(2)观察一个长方体时,当眼睛在长方体的一个顶点时,能看到的面最多,最多只有3个面;
(3)线段有2个端点,不能向两端无限延伸,能测量长度;直线没有端点,可以向两端无限延伸,不能测量长度;射线有1个端点,可以向一端无限延伸,不能测量长度。
【详解】A.如上图这样测量跳远成绩,是因为点到直线的距离最短,原题说法正确;
B.观察一个长方体纸箱,一次最多能看到3个面,原题说法错误;
C.把一条长8厘米的线段向一边延长100厘米后,还是一条线段,原题说法错误。
故答案为:A
【点睛】此题涉及的知识点较多,但都比较简单,属于基础题,只要认真,容易完成,注意平时基础知识的积累。
3.C
【分析】A选项射线有一个端点,另一端可以无限延伸,射线本身就是无限长的,不能说向一端延长一定长度后得到射线。由此解答。
B选项先找出下午3时30分钟面上时针和分针所在的位置,再进行解答。
C选项根据商不变规律,被除数和除数同时乘或除以相同的数(0 除外),商不变。由此解答。
D选项根据1升=1000毫升,换算后进行解答。
【详解】A.把一条线段向一端延长100米,就得到一条射线,射线不可度量;原题说法错误;
B.下午3时30分,钟面上分针和时针所夹的角是直角,如果时针在3上,分针在6上,钟面上分针和时针所夹的角是直角,但下午3时30分,分针在6上,时针在3和4之间,所以应小于90°;原题说法错误;
C.根据商不变性质,810÷5=(810×2)÷(5×2),说法正确;
D.1升=1000毫升,因此2升=2000毫升。2升雪碧的容量和2000毫升可乐的容量一样;原题说法错误;
故答案为:C
4.B
【分析】同一平面内,不相交的两条直线互相平行;垂直于同一条直线的两直线平行,据此逐项判断。
【详解】A.没有平行线;
B.有3组平行线;
C.有2组平行线;
D.有1组平行线;
故答案为:B
【点睛】要找平行线,就是找不相交的两条线段。
5.D
【分析】1平角是180°,根据图示可知,∠1+∠1+∠2+∠2=180°,因此用180°减去2个∠1后,再除以2即可,依此计算。
【详解】180°-25°-25°=130°
130°÷2=65°
即∠2=65°。
故答案为:D
6.C
【分析】狐狸要想不被老虎抓住,不能逃向老虎所在的岸边,应向对岸逃去。只有OC和OD可以选择。从直线外一点到这条直线所画的垂直线段的长度,叫做点到直线的距离。垂直线段最短。据此可以解答。
【详解】由分析知,OC这条垂线就是狐狸的逃生路线。
故答案为:C
7.A
【分析】在同一平面内的两条不重合的直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况。
【详解】由分析得:
在同一平面内,两条直线的位置关系正确的是。
故答案为:A
【点睛】本题考查同一平面内两条直线的位置关系,注意垂直只是相交的特殊情况。
8.B
【分析】根据长方形的特征,对边平行且相等,4个角都是直角,可知,长方形相邻的两条边互相垂直,相对的两边互相平行。
【详解】根据分析可知:
正方形相邻两边互相垂直,相对的两边互相平行。
故答案为:B
【点睛】此题主要考查长方形的特征以及平行、垂直的定义,应熟练掌握。
9. 47 133°
【分析】观察上图,∠1和∠2拼成一个直角,用90°-∠1,求出∠2;∠3和∠2拼成一个平角,用180°-∠2,求出∠3,据此解答。
【详解】90°-43°=47°,则∠2=47°;
180°-47°=133°,则∠3=133°。
10. 60 平
【分析】钟面上有12个大格,1个大格的所对的夹角的度数是30度,2时,分针指向12,时针指向2,所以时针与分针的夹角是2个大格,用乘法即可解答;
6时整,时针指向6,分针指向12,中间6格,据此即可解答。
【详解】360÷12=30(度),30×2=60(度),因此钟面上2时整,时针和分针组成的角是60度。
30×6=180(度),钟面上6时整,时针和分针组成的角是180度,也就是平角。
11. × + =
【分析】在同一个平面内,不相交的两条直线叫做平行线;两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直。既不互相平行也不互相垂直的两条直线就相交。据此解答即可。
【详解】(×)
(+)
(=)
【点睛】此题考查了垂直与平行的特征和性质,要熟练掌握。
12.30
【分析】观察上图可知:2个∠1和1个∠2组成一个平角,用180°减去2个75°,即可求出∠2的度数。
【详解】180°-2×75°
=180°-150°
=30°
∠2=30°。
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角),以及它与各角之间的关系,利用已知角,求出未知角。
13. 300 4 8 2
【分析】1分=60秒,60分=1时,1000毫升=1升,由高级单位化低级单位乘进率,由低级单位化高级单位除以进率;1平角=180°,1直角=90°,据此计算1平角等于多少直角。
【详解】5分=300秒 240分=4时
8000毫升=8升 1平角=2直角
【点睛】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
14. 锐 300
【分析】6:45时分针指向9,时针指向6和7之间,这时时针和分针所成的角小于90°,所以这时钟面上的时针和分针成锐角;从晚上8:45到次日6:45共10小时。每小时转30°,10小时转动 10×30°=300°。
【详解】6:45时分针指向9,时针指向6和7之间,这时钟面上的时针和分针成锐角;
晚上12:45-晚上8:45=4(小时)
次日6:45-凌晨0:45=6(小时)
4+6=10(小时)
10×30°=300°
时针转动了300度。
15. 锐 75 钝 150
【分析】大于0°小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角;
一副三角尺有90°、45°、45°,90°、60°、30°几个角,分别从每个三角尺中任取一个角,进行加或减,拼出不同的角;据此计算角的度数,再根据角的分类解题即可。
【详解】30°+45°=75°
锐角,75°。
60°+90°=150°
钝角,150°。
16. 直线 直线 射线 平行或垂直
【分析】线段有两个端点,长度有限可以测量长度;射线只有一个端点,可以向一端无限延长,长度无限无法测量长度;直线没有端点,可以向两端无限延长,长度无限无法测量长度;
在同一平面内不相交的两条直线互相平行,在同一平面内相交成直角的两条直线互相垂直;把长方形对折再对折,如果两次对折的方向相同,则两条折痕不会相交,即互相平行,如果两次对折的方向不同,即一次沿长对折,一次沿宽对折,则两条折痕会相交成直角,即互相垂直。据此解答。
【详解】根据分析可知:
把线段的两端都无限延长,就得到一条直线。直线和射线都是无限长的。把一个长方形纸对折再对折,两条折痕互相平行或垂直。
17.×
【分析】用放大镜看物体,只是改变了看到物体的视角,即改变了眼睛看到物体的大小,但是物体的形状并不会改变,看角也是一样的,角的形状是不变的,即角两边叉开的大小是不变的,所以原来是6°的角经过放大后还是6°的角,据此判断即可。
【详解】用10倍的放大镜看6°的角放大后还是6°的角,并不会变成60°的角。
故答案为:×
18.√
【分析】同一平面内,两条直线相交成直角,这两条直线互相垂直;同一平面内,永不相交的两条直线叫做平行线,组成平行线的两条直线互相平行;依此画图并判断。
【详解】画图如下:
由此可知,把一个正方形纸对折两次,两条折痕可能互相垂直,也可能互相平行。原题表述正确。
故答案为:√
19.√
【分析】根据直线、射线和线段的含义:直线没有端点,可以向两端无限延伸,不能量出长度;射线只有一个端点,只能向一端无限延伸,不能量出长度;线段有两个端点,不能向两端延伸,可以量出长度;据此解答即可。
【详解】射线只有一个端点,可以向一端无限延伸,因此无法测量其长度,因为长度是有限的,而射线是无限的,所以无法用具体的数值表示射线的长度;故原题说法正确。
故答案为:√
20.×
【分析】锐角:大于0度小于90度的角;钝角:大于90度小于180度的角;直角:等于90度的角;平角:等于180度的角;周角:等于360度的角;据此解答即可。
【详解】平角等于180度,大于90度小于180度的角是钝角;
小于180度的角是钝角,说法错误,因为锐角、直角、钝角都小于180度;所以原题说法错误。
故答案为:×
21.√
【分析】在同一平面内,如果两条直线都和第三条直线平行,则这两条直线也相互平行。
【详解】因在同一平面内,直线a和直线b相互平行,直线a和直线c相互平行,直线b和c都和直线a平行,所以直线b和直线c相互平行。原题说法正确。
故答案为:√
22.×
【分析】在同一平面内的两条不重合的直线,只有两种位置关系,即相交或平行,而垂直是相交的一种特殊情况。据此分析作答。
【详解】在同一平面内,两条直线永远不相交的情况即为平行,两条直线交于一点的情况即为相交,当两条直线交于一点且夹角为90度即为垂直,所以垂直为相交的一种特殊情况,所以在同一平面内,两条直线的位置关系有相交和平行。
故答案为:×
23.∠1的度数是60°;∠2的度数是30°;∠3的度数是60°
【分析】根据题图可知,先根据∠1+30°=90°求出∠1的度数,∠1和∠2组成的角也是直角,等于90°,据此计算出∠2的度数;∠3和∠2组成的角也是直角,等于90°,据此计算出∠3的度数;据此解答。
【详解】根据分析可得:
∠1+30°=90°,所以∠1=90°-30°=60°
∠2=90°-∠1=90°-60°=30°
∠3=90°-∠2=90°-30°=60°
∠1的度数是60°;∠2的度数是30°;∠3的度数是60°。
24.125;41
【分析】根据混合运算计算法则:
(1)先计算乘除,再计算加法;
(2)先计算小括号里的减法,再计算中括号里的除法,最后计算中括号外的除法。
【详解】8×15+340÷68
=120+5
=125
246÷[96÷(856-840)]
=246÷[96÷16]
=246÷6
=41
25.见详解
【分析】过直线外一点作已知直线的平行线的方法:先把三角尺的一条直角边与已知直线重合;再用直尺紧靠着三角尺的另一条直角边。固定直尺,然后沿着直尺平移三角尺,使直线外的点在三角尺上。沿直角边画出另一条直线即可;过直线上或直线外一点作垂线的方法:先把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上。再沿三角尺的另一条直角边画一条直线,并画上垂直符号。这条直线就是已知直线的垂线。
【详解】
如图:
26.画图见详解;4
【分析】过直线上或直线外一点作垂线:先把三角尺的一条直角边与已知直线重合,然后将三角尺沿着直线移动,使得直线上或直线外的已知点在三角尺的另一条直角边上,最后沿三角尺的另一条直角边画一条直线,并画上直角符号,这条直线就是已知直线的垂线。然后用尺子量出垂线段的长度就是所求距离。
【详解】
点O到直线L的距离是4厘米。
【点睛】本题考查了过直线外一点作垂线的方法,点到直线的垂线段的长度就是点到直线的距离。
27.见详解
【分析】先用直尺的边与这条直线重合,在直尺的0刻度线处点上一点,再在4厘米处点上另外一点,这两点间的距离就是4厘米;
线段有两个端点,有限长,能用直尺测量出长度;直线没有端点,可以向两边无限延长,无法测量长度;据此解答即可。
【详解】作图如下:
线段和直线的关系:在直线上点上不同的两点,这两点之间的一段叫做线段;把线段的两端无限延长,就能得到一条直线。
28.34°
【分析】
如图,长方形纸的一个角折叠,使∠1=∠3,观察图可以发现,∠1、∠2和∠3这个三角组成直角,直角为90°,用90°依次减去∠1和∠3,即可求出∠2的度数,据此解答即可。
【详解】90°-28°-28°
=62°-28°
=34°
答:∠2的度数为34°。
29.可以;无数条
【分析】在平面上,过一点可以画无数条直线,不能确定一条直线;只有过两点才能确定一条直线,据此解答。
【详解】用一个图钉把一张硬纸条钉在木板上,硬纸条可以转动,过一点可以画无数条直线。
30.45°;45°
【分析】长方形和正方形的四个角都是直角,直角是90°。长方形的长刚好把正方形平均分成两个三角形。所以中间共用的角是45°,据此可以算出∠1和∠2的度数。
【详解】∠1=90°-45°=45°
∠2=90°-45°=45°
答:∠1是45°,∠2也是45°。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
