陕西省榆林市第三中学2024-2025学年高一下学期期中质量检测数学试题(图片版,含详解)
文档属性
| 名称 | 陕西省榆林市第三中学2024-2025学年高一下学期期中质量检测数学试题(图片版,含详解) |  | |
| 格式 | |||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 18:50:14 | ||
图片预览



文档简介
陕西省榆林市第三中学 2024-2025 学年高一下学期
期中质量检测数学试题
一、单选题
1. 已知集合 , ,则 ( )
A. B. C. D.
2. 已知复数 ,则( )
A. 的虚部为 B.
C. D.
3. 已知平面向量 , ,若 ,则 ( )
A. B. C. D.
4. 已知 m,n,l为三条不同的直线, , 为两个不同的平面,若 , ,
,且 m与 n异面,则( )
A.l至多与 m,n中的一条相交 B.l与 m,n均相交
C.l与 m,n均平行 D.l至少与 m,n中的一条相交
5. 已知 , , ,则( )
A. B. C. D.
6. 在 中,内角 A,B,C的对边分别为 a,b,c,且 , ,
,则 ( )
D.
A. B. C.
7. 如图是一个正方体的展开图,若将它还原为正方体,则( )
A. B. C.EI与 BG共面 D.AF与 BG异面
8. 中国冶炼铸铁的技术起源于春秋时期,并在战国时期取得了显著的进步,推
动了当时社会的发展.现将一个半径为 2cm 的实心铁球熔化后,浇铸成一个圆台
状的实心铁锭(不考虑损耗),若该圆台的一个底面周长是另一个底面周长的 2
倍,高为 2cm,则该圆台的表面积为( )
A. B. C. D.
二、多选题
9. 下列关于空间几何体的叙述错误的是( )
A.底面是正方形的棱锥是正四棱锥
B.任何一个几何体都必须有顶点、棱和面
C.有两个面互相平行,其余各面都是梯形的多面体是棱台
D.一个棱柱至少有 5个面
10. 已知三个非零向量 ,则下列命题正确的是( )
A.若 ,则
B.若 ,则
C.若 ,则 或
D.若 ,则
11. 若 是复数,则下列说法错误的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则 或
三、填空题
12. 用斜二测画法作一个水平放置的平行四边形的直观图,若直观图是一个角为
,边长为 2的菱形,则原来的平行四边形的面积为______.
13. 若 ,则 _____.
14. 如图,正方体 的棱长为 2,N为 的中点,若过 的平
面 平面 ,则 截该正方体所得截面图形的面积为__________.
四、解答题
15. 已知复数 , ( , 为虚数单位).
(1)若 为纯虚数,求实数 的值;
(2)若 在复平面内所对应的点位于第四象限,求 的取值范围.
16. 在 中,内角 所对的边分别为 ,且
.
(1)求角 的大小;
(2)若 ,判断 的形状并说明理由.
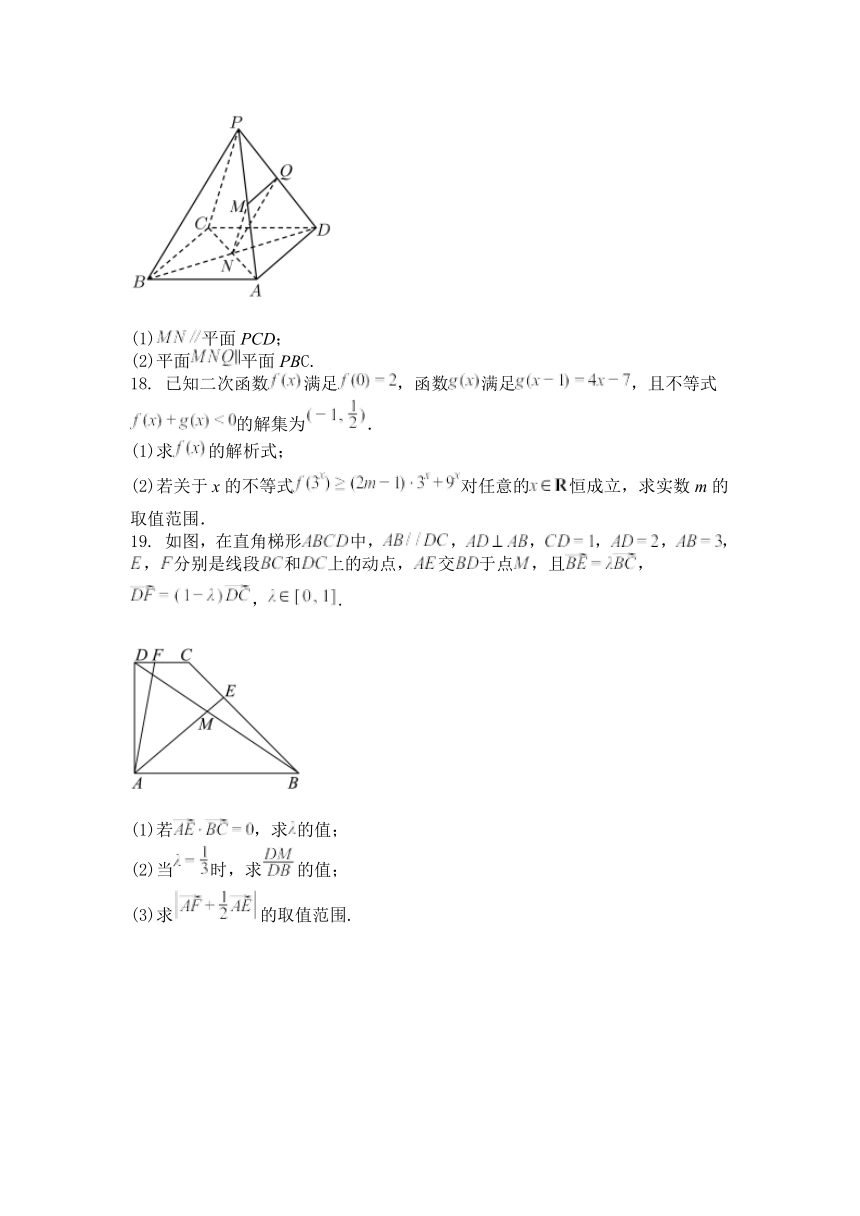
17. 如图,已知四棱锥 中,底面 ABCD为平行四边形,点 M、N、Q
分别是 PA、BD、PD的中点.求证:
(1) 平面 PCD;
(2)平面 平面 PBC.
18. 已知二次函数 满足 ,函数 满足 ,且不等式
的解集为 .
(1)求 的解析式;
(2)若关于 x的不等式 对任意的 恒成立,求实数 m的
取值范围.
19. 如图,在直角梯形 中, , , , , ,
, 分别是线段 和 上的动点, 交 于点 ,且 ,
, .
(1)若 ,求 的值;
(2)当 时,求 的值;
(3)求 的取值范围.
陕西省榆林市第三中学 2024-2025 学年高一下学期期中质量检测数学试题
整体难度:适中
考试范围:集合与常用逻辑用语、等式与不等式、复数、平面向量、空间向量与立体几何、
函数与导数、三角函数与解三角形
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
容易 3
较易 8
适中 8
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.85 交集的概念及运算;解不含参数的一元二次不等式
2 0.85 求复数的实部与虚部;求复数的模;共轭复数的概念及计算
3 0.94 向量垂直的坐标表示;利用向量垂直求参数
4 0.94 面面关系有关命题的判断;异面直线的概念及辨析
5 0.65 比较指数幂的大小;比较对数式的大小
6 0.85 正弦定理解三角形;已知正(余)弦求余(正)弦
7 0.85 棱柱的结构特征和分类;异面直线的判定;空间中的点(线)共面问题
圆台的结构特征辨析;圆台表面积的有关计算;台体体积的有关计算;球的体积
8 0.85
的有关计算
二、多选题
棱柱的结构特征和分类;棱锥的结构特征和分类;棱台的结构特征和分类;球的
9 0.65
结构特征辨析
平面向量的概念与表示;向量数乘的有关计算;数量积的运算律;垂直关系的向
10 0.65
量表示
11 0.85 求复数的模;复数的除法运算;复数代数形式的乘法运算;复数的乘方
三、填空题
12 0.85 斜二测画法中有关量的计算
13 0.85 正、余弦齐次式的计算;给值求值型问题
14 0.65 判断正方体的截面形状
四、解答题
已知复数的类型求参数;复数的除法运算;复数加减法的代数运算;根据复数对
15 0.65
应坐标的特点求参数
正弦定理边角互化的应用;正、余弦定理判定三角形形状;余弦定理解三角形;
16 0.65
余弦定理边角互化的应用
17 0.94 判断线面平行;证明面面平行
18 0.65 求二次函数的解析式;函数不等式恒成立问题;求指数函数在区间内的值域;由
一元二次不等式的解确定参数
数量积的运算律;已知数量积求模;用定义求向量的数量积;利用平面向量基本
19 0.65
定理求参数
知识点分析
序号 知识点 对应题号
1 集合与常用逻辑用语 1
2 等式与不等式 1,18
3 复数 2,11,15
4 平面向量 3,10,19
5 空间向量与立体几何 4,7,8,9,12,14,17
6 函数与导数 5,18
7 三角函数与解三角形 6,13,16
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
期中质量检测数学试题
一、单选题
1. 已知集合 , ,则 ( )
A. B. C. D.
2. 已知复数 ,则( )
A. 的虚部为 B.
C. D.
3. 已知平面向量 , ,若 ,则 ( )
A. B. C. D.
4. 已知 m,n,l为三条不同的直线, , 为两个不同的平面,若 , ,
,且 m与 n异面,则( )
A.l至多与 m,n中的一条相交 B.l与 m,n均相交
C.l与 m,n均平行 D.l至少与 m,n中的一条相交
5. 已知 , , ,则( )
A. B. C. D.
6. 在 中,内角 A,B,C的对边分别为 a,b,c,且 , ,
,则 ( )
D.
A. B. C.
7. 如图是一个正方体的展开图,若将它还原为正方体,则( )
A. B. C.EI与 BG共面 D.AF与 BG异面
8. 中国冶炼铸铁的技术起源于春秋时期,并在战国时期取得了显著的进步,推
动了当时社会的发展.现将一个半径为 2cm 的实心铁球熔化后,浇铸成一个圆台
状的实心铁锭(不考虑损耗),若该圆台的一个底面周长是另一个底面周长的 2
倍,高为 2cm,则该圆台的表面积为( )
A. B. C. D.
二、多选题
9. 下列关于空间几何体的叙述错误的是( )
A.底面是正方形的棱锥是正四棱锥
B.任何一个几何体都必须有顶点、棱和面
C.有两个面互相平行,其余各面都是梯形的多面体是棱台
D.一个棱柱至少有 5个面
10. 已知三个非零向量 ,则下列命题正确的是( )
A.若 ,则
B.若 ,则
C.若 ,则 或
D.若 ,则
11. 若 是复数,则下列说法错误的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则 或
三、填空题
12. 用斜二测画法作一个水平放置的平行四边形的直观图,若直观图是一个角为
,边长为 2的菱形,则原来的平行四边形的面积为______.
13. 若 ,则 _____.
14. 如图,正方体 的棱长为 2,N为 的中点,若过 的平
面 平面 ,则 截该正方体所得截面图形的面积为__________.
四、解答题
15. 已知复数 , ( , 为虚数单位).
(1)若 为纯虚数,求实数 的值;
(2)若 在复平面内所对应的点位于第四象限,求 的取值范围.
16. 在 中,内角 所对的边分别为 ,且
.
(1)求角 的大小;
(2)若 ,判断 的形状并说明理由.
17. 如图,已知四棱锥 中,底面 ABCD为平行四边形,点 M、N、Q
分别是 PA、BD、PD的中点.求证:
(1) 平面 PCD;
(2)平面 平面 PBC.
18. 已知二次函数 满足 ,函数 满足 ,且不等式
的解集为 .
(1)求 的解析式;
(2)若关于 x的不等式 对任意的 恒成立,求实数 m的
取值范围.
19. 如图,在直角梯形 中, , , , , ,
, 分别是线段 和 上的动点, 交 于点 ,且 ,
, .
(1)若 ,求 的值;
(2)当 时,求 的值;
(3)求 的取值范围.
陕西省榆林市第三中学 2024-2025 学年高一下学期期中质量检测数学试题
整体难度:适中
考试范围:集合与常用逻辑用语、等式与不等式、复数、平面向量、空间向量与立体几何、
函数与导数、三角函数与解三角形
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
容易 3
较易 8
适中 8
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.85 交集的概念及运算;解不含参数的一元二次不等式
2 0.85 求复数的实部与虚部;求复数的模;共轭复数的概念及计算
3 0.94 向量垂直的坐标表示;利用向量垂直求参数
4 0.94 面面关系有关命题的判断;异面直线的概念及辨析
5 0.65 比较指数幂的大小;比较对数式的大小
6 0.85 正弦定理解三角形;已知正(余)弦求余(正)弦
7 0.85 棱柱的结构特征和分类;异面直线的判定;空间中的点(线)共面问题
圆台的结构特征辨析;圆台表面积的有关计算;台体体积的有关计算;球的体积
8 0.85
的有关计算
二、多选题
棱柱的结构特征和分类;棱锥的结构特征和分类;棱台的结构特征和分类;球的
9 0.65
结构特征辨析
平面向量的概念与表示;向量数乘的有关计算;数量积的运算律;垂直关系的向
10 0.65
量表示
11 0.85 求复数的模;复数的除法运算;复数代数形式的乘法运算;复数的乘方
三、填空题
12 0.85 斜二测画法中有关量的计算
13 0.85 正、余弦齐次式的计算;给值求值型问题
14 0.65 判断正方体的截面形状
四、解答题
已知复数的类型求参数;复数的除法运算;复数加减法的代数运算;根据复数对
15 0.65
应坐标的特点求参数
正弦定理边角互化的应用;正、余弦定理判定三角形形状;余弦定理解三角形;
16 0.65
余弦定理边角互化的应用
17 0.94 判断线面平行;证明面面平行
18 0.65 求二次函数的解析式;函数不等式恒成立问题;求指数函数在区间内的值域;由
一元二次不等式的解确定参数
数量积的运算律;已知数量积求模;用定义求向量的数量积;利用平面向量基本
19 0.65
定理求参数
知识点分析
序号 知识点 对应题号
1 集合与常用逻辑用语 1
2 等式与不等式 1,18
3 复数 2,11,15
4 平面向量 3,10,19
5 空间向量与立体几何 4,7,8,9,12,14,17
6 函数与导数 5,18
7 三角函数与解三角形 6,13,16
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
同课章节目录
