5.3.1函数的单调性 课件(共21张PPT)
文档属性
| 名称 | 5.3.1函数的单调性 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 21:20:36 | ||
图片预览





文档简介
(共21张PPT)
5.3.1
函数的单调性
问题引入
判断函数 在 上的单调性.
解:
如何运用已有知识解决?
任意 , 且 ;
函数单调性定义:
函数 在区间 内是
理论分析
增函数.
即:
即证:
任意 ,当 时,都有 ;
函数单调性定义:
函数 在区间 内是
(函数的平均变化率)
导数
(瞬时变化率)
减函数.
理论分析
任意 , 当 时,都有 ;
即:
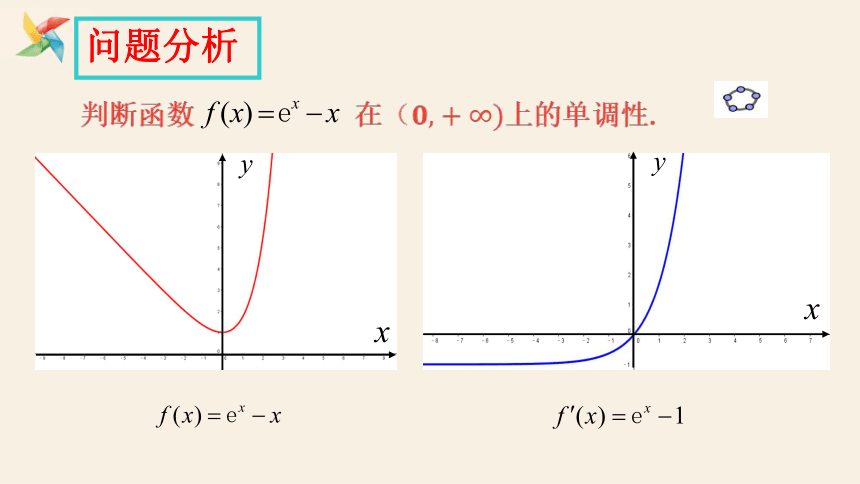
问题分析
判断函数 在上的单调性.
合作探究
(1)画出函数图像;
(3)观察函数单调性与导数正负的关系.
(2)求导函数并画出图象;
(1)
(2)
(3)
(4)
函数的单调性
导数的正负
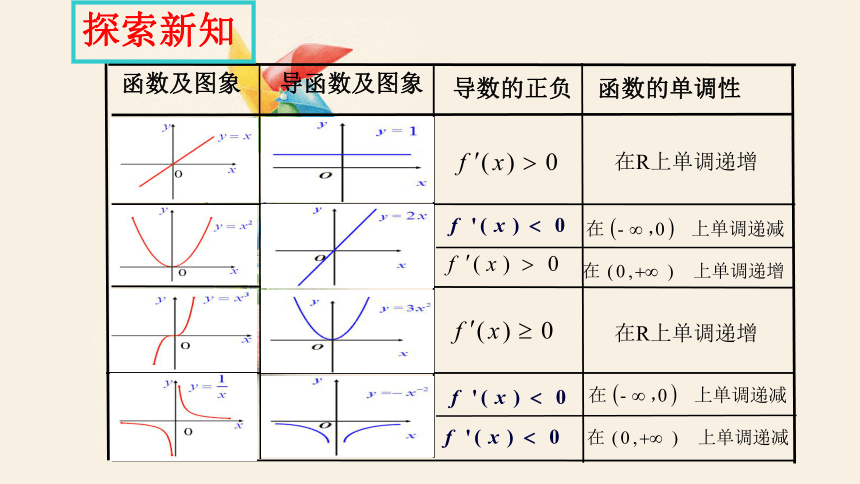
函数及图象
探索新知
导函数及图象
在R上单调递增
在R上单调递增
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
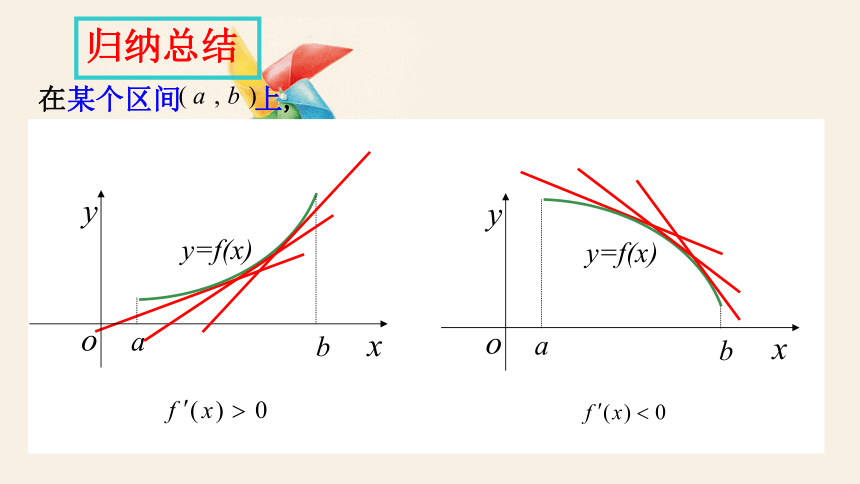
归纳总结
在某个区间 上,
结论总结
函数的单调性与其导函数正负的关系:
区间必须是在定义域内的某个区间.
在某个区间 上,
如果 , 那么 在 上单调递增;
如果 ,那么 在 上单调递减;
若恒有
令
得
令
得
单调递增区间为
单调递减区间为
解:
函数的定义域为
问题解决
求出函数 的单调区间.
如何运用导数知识解决?
高台跳水
高台跳水运动员的高度h随时间t变化的函数
h
t
o
a
b
v
t
o
b
a
问题解决
用导数求单调区间的方法:
运用新知
例1:求出函数 的单调区间,画出函数的大致图象.
解:
令
得
令
得
单调递增区间为
单调递减区间为
函数的定义域为
运用新知
例1:求出函数 的单调区间,画出函数的大致图象.
跟踪训练
练习1:求下列函数的单调性.
(2)求导函数 ;
(1)确定函数 的定义域;
(3)解不等式 ,解集在定义域内的部分为增区间;
(4)解不等式 ,解集在定义域内的部分为减区间.
方法归纳
利用导数求函数
单调区间的步骤?
用导数求单调区间的方法:
运用新知
例2:函数图像如下图,导函数图像可能为哪一个?
跟踪训练
练习2:导函数图像如下图,则函数图像可能为( )
知识
方法
思想
感悟
归纳小结
课后作业
必做题:教材P87 练习 1、2、3 题;
结合所学知识,举几个函数实例,比较定义法、图像法、导数法求单调区间的特点.
选做题:
体会数学
数与形,本是相倚依,焉能分作两边飞;
数无形时少直觉,形少数时难入微;
数形结合百般好,隔离分家万事休;
切莫忘,
几何代数统一体,永远联系莫分离.
——华罗庚
感谢观看!
5.3.1
函数的单调性
问题引入
判断函数 在 上的单调性.
解:
如何运用已有知识解决?
任意 , 且 ;
函数单调性定义:
函数 在区间 内是
理论分析
增函数.
即:
即证:
任意 ,当 时,都有 ;
函数单调性定义:
函数 在区间 内是
(函数的平均变化率)
导数
(瞬时变化率)
减函数.
理论分析
任意 , 当 时,都有 ;
即:
问题分析
判断函数 在上的单调性.
合作探究
(1)画出函数图像;
(3)观察函数单调性与导数正负的关系.
(2)求导函数并画出图象;
(1)
(2)
(3)
(4)
函数的单调性
导数的正负
函数及图象
探索新知
导函数及图象
在R上单调递增
在R上单调递增
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
归纳总结
在某个区间 上,
结论总结
函数的单调性与其导函数正负的关系:
区间必须是在定义域内的某个区间.
在某个区间 上,
如果 , 那么 在 上单调递增;
如果 ,那么 在 上单调递减;
若恒有
令
得
令
得
单调递增区间为
单调递减区间为
解:
函数的定义域为
问题解决
求出函数 的单调区间.
如何运用导数知识解决?
高台跳水
高台跳水运动员的高度h随时间t变化的函数
h
t
o
a
b
v
t
o
b
a
问题解决
用导数求单调区间的方法:
运用新知
例1:求出函数 的单调区间,画出函数的大致图象.
解:
令
得
令
得
单调递增区间为
单调递减区间为
函数的定义域为
运用新知
例1:求出函数 的单调区间,画出函数的大致图象.
跟踪训练
练习1:求下列函数的单调性.
(2)求导函数 ;
(1)确定函数 的定义域;
(3)解不等式 ,解集在定义域内的部分为增区间;
(4)解不等式 ,解集在定义域内的部分为减区间.
方法归纳
利用导数求函数
单调区间的步骤?
用导数求单调区间的方法:
运用新知
例2:函数图像如下图,导函数图像可能为哪一个?
跟踪训练
练习2:导函数图像如下图,则函数图像可能为( )
知识
方法
思想
感悟
归纳小结
课后作业
必做题:教材P87 练习 1、2、3 题;
结合所学知识,举几个函数实例,比较定义法、图像法、导数法求单调区间的特点.
选做题:
体会数学
数与形,本是相倚依,焉能分作两边飞;
数无形时少直觉,形少数时难入微;
数形结合百般好,隔离分家万事休;
切莫忘,
几何代数统一体,永远联系莫分离.
——华罗庚
感谢观看!
