云南省西双版纳傣族自治州景洪市曲靖一中景洪学校2024-2025学年高二下学期期中检测数学试卷(PDF版,含解析)
文档属性
| 名称 | 云南省西双版纳傣族自治州景洪市曲靖一中景洪学校2024-2025学年高二下学期期中检测数学试卷(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-29 21:42:09 | ||
图片预览




文档简介
云南省西双版纳傣族自治州景洪市曲靖一中景洪学校
2024-2025 学年高二下学期期中检测数学试卷
一、单选题
1. 设集合 ,集合 ,则 ( )
A. B.
C. D.
2
2. 函数 y= x ㏑ x 的单调递减区间为
A.( 1,1] B.(0,1] C.[1,+∞) D.(0,+∞)
3. 等差数列 中,若 , 为方程 的两根,则 等
于( )
A.10 B.15 C.20 D.40
4. 如图,在三棱锥 中,点 , 分别是 , 的中点,点 满足 ,
若 ,则 ( )
A.
B.
C.
D.
5. 已知直线 : 与圆 : 交于 ,两点,则
的一个充分不必要条件是( )
A. B. C. D.
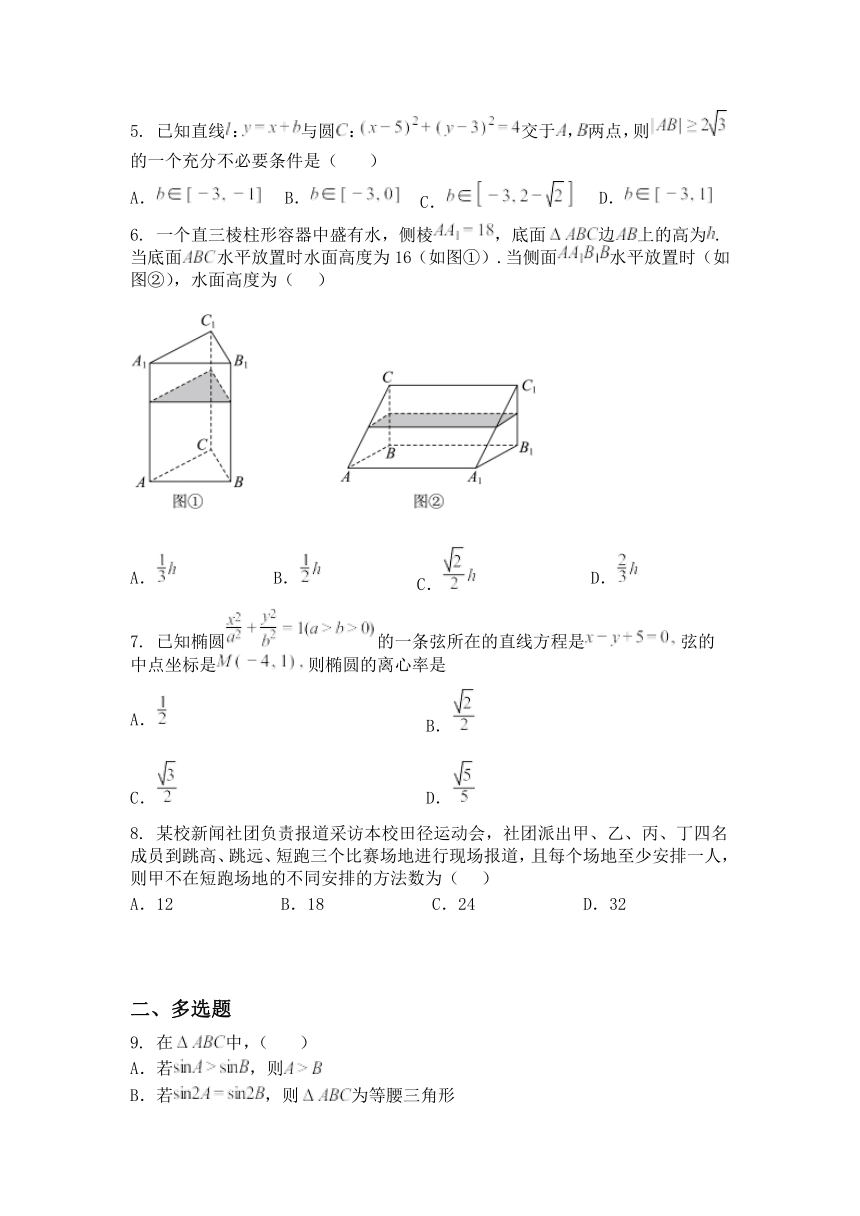
6. 一个直三棱柱形容器中盛有水,侧棱 ,底面 边 上的高为 .
当底面 水平放置时水面高度为 16(如图①).当侧面 水平放置时(如
图②),水面高度为( )
A. B. C. D.
7. 已知椭圆 的一条弦所在的直线方程是 弦的
中点坐标是 则椭圆的离心率是
A. B.
C. D.
8. 某校新闻社团负责报道采访本校田径运动会,社团派出甲、乙、丙、丁四名
成员到跳高、跳远、短跑三个比赛场地进行现场报道,且每个场地至少安排一人,
则甲不在短跑场地的不同安排的方法数为( )
A.12 B.18 C.24 D.32
二、多选题
9. 在 中,( )
A.若 ,则
B.若 ,则 为等腰三角形
C.若 ,则 为钝角三角形
D.若 是锐角, ,则 为锐角三角形
10. 已知 , 是 的共轭复数,则( )
A.若 ,则
B.若 为纯虚数,则
C.若 ,则
D.若 ,则集合 所构成区域的面积为
11. 已知函数 ,若关于 的方程 有四个
不同的根,它们从小到大依次记为 , , , ,则( )
A. B.
C. D.函数 有 6个零点
三、填空题
12. 如图为函数 的部分图
象,则 的值为_____
13. 在 的展开式中,各项系数之和为 ,则展开式中的常数项为
__________________.
14. 如图,一个圆环分成 , , , 四个区域,用 3种颜色(全部用完)对这
四个区域涂色,要求相邻区域不同色,则不同涂色的方法种数为____________.
(用数字作答)
四、解答题
15. 随着科技的进步,近年来,我国新能源汽车产业迅速发展,各大品牌新能源
汽车除了靠不断提高汽车的性能和质量来提升品牌竞争力,在广告投放方面的花
费也是逐年攀升.某校数学兴趣小组对某品牌新能源汽车近 5 年的广告费投入
(单位:亿元)进行了统计, 具体数据见下表:
年份代号 1 2 3 4 5
广告费投入 4.85.66. 27. 68. 8
并随机调查了 400 名市民对该品牌新能源汽车的认可情况,得到的部分数据见
下表:
认可不认可
50 岁以下 140 60
50 岁及以上 120 80
(1)求广告费投入 与年份代号 之间的线性经验回归方程;
(2)依据小概率值 的 独立性检验,能否认为市民的年龄与对该品牌新能
源汽车的认可度有关联
附: ① 经验回归方程 中, ;
② ,其中 .
0.1 0.05 0.01 0.005 0.001
2.7063.8416.6357.87910.828
16. 如图 1在直角梯形 中, , , , ,
E 是 AD 的中点,O 是 AC 与 BE 的交点,将 沿 BE 折起到图 2中 的
位置,得到四棱锥 .
(1)证明: 平面 ;
(2)当平面 平面 ,求平面 与平面 夹角的余弦值.
17. 已知函数 ( ).
(1)若 ,求函数 的极值;
(2)求证: .
18. 为响应国家促进消费的政策,某大型商场举办了“消费满减乐翻天”的优惠
活动,顾客消费满 800 元(含 800 元)可抽奖一次,抽奖方案有两种(顾客只能
选择其中的一种)
方案 1:从装有 5个红球,3个蓝球(形状、大小完全相同)的抽奖盒中,有放
回地依次摸出 3个球.每摸出 1次红球,立减 150 元,若 3次都摸到红球,则额
外再减 200 元(即总共减 650 元);
方案 2:从装有 5个红球,3个蓝球(形状、大小完全相同)的抽奖盒中,不放
回地依次摸出 3个球.中奖规则为:若摸出 3个红球,享受免单优惠;若摸出 2
个红球,则打 5折;其余情况无优惠.
(1)顾客 A 选择抽奖方案 2,已知他第一次摸出红球,求他能够享受优惠的概率;
(2)顾客 B 恰好消费了 800 元,
①若他选择抽奖方案 1,求他实付金额的分布列和期望(结果精确到 0.01);
②试从实付金额的期望值分析顾客 B 选择何种抽奖方案更合理.
19. 17 世纪荷兰数学家舒腾设计了多种圆锥曲线规,其中的一种如图 1所示.四
根等长的杆用铰链首尾链接,构成菱形 .带槽杆 长为 ,点 , 间
的距离为 2,转动杆 一周的过程中始终有 .点 M 在线段 的延
长线上,且 .
(1)建立如图 2所示的平面直角坐标系,求出点 E 的轨迹Γ的方程;
(2)过点 的直线 与Γ交于 A、B 两点.记直线 MA、MB 的斜率为 、 ,证明:
为定值.
云南省西双版纳傣族自治州景洪市曲靖一中景洪学校 2024-2025 学年高二下
学期期中检测数学试卷
整体难度:适中
考试范围:集合与常用逻辑用语、函数与导数、数列、空间向量与立体几何、平面解析几何、
计数原理与概率统计、三角函数与解三角形、复数
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
容易 2
较易 7
适中 9
较难 1
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.94 交并补混合运算
2 0.94 利用导数求函数的单调区间(不含参)
3 0.85 利用等差数列的性质计算
4 0.85 空间向量加减运算的几何表示;空间向量数乘运算的几何表示
判断命题的充分不必要条件;由直线与圆的位置关系求参数;求点到直线的距离;
5 0.65
圆的弦长与中点弦
6 0.85 柱体体积的有关计算
7 0.65 求椭圆的离心率或离心率的取值范围
分组分配问题;分类加法计数原理;分步乘法计数原理及简单应用;元素(位置)
8 0.65
有限制的排列问题
二、多选题
9 0.85 正弦定理解三角形;正、余弦定理判定三角形形状
复数的基本概念;与复数模相关的轨迹(图形)问题;共轭复数的概念及计算;
10 0.65
复数的除法运算
函数图象的应用;根据函数零点的个数求参数范围;函数与方程的综合应用;求
11 0.4
函数零点或方程根的个数
三、填空题
12 0.85 由图象确定正(余)弦型函数解析式
13 0.85 求指定项的系数;二项展开式各项的系数和
14 0.85 涂色问题
四、解答题
15 0.65 求回归直线方程;独立性检验解决实际问题
16 0.65 证明线面垂直;面面角的向量求法
17 0.65 求已知函数的极值;利用导数研究不等式恒成立问题;利用导数证明不等式
18 0.65 计算古典概型问题的概率;计算条件概率;超几何分布的均值;二项分布的均值
根据 a、b、c 求椭圆标准方程;根据韦达定理求参数;根据直线与椭圆的位置
19 0.65
关系求参数或范围;椭圆中的定值问题
知识点分析
序号 知识点 对应题号
1 集合与常用逻辑用语 1,5
2 函数与导数 2,11,17
3 数列 3
4 空间向量与立体几何 4,6,16
5 平面解析几何 5,7,19
6 计数原理与概率统计 8,13,14,15,18
7 三角函数与解三角形 9,12
8 复数 10
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
2024-2025 学年高二下学期期中检测数学试卷
一、单选题
1. 设集合 ,集合 ,则 ( )
A. B.
C. D.
2
2. 函数 y= x ㏑ x 的单调递减区间为
A.( 1,1] B.(0,1] C.[1,+∞) D.(0,+∞)
3. 等差数列 中,若 , 为方程 的两根,则 等
于( )
A.10 B.15 C.20 D.40
4. 如图,在三棱锥 中,点 , 分别是 , 的中点,点 满足 ,
若 ,则 ( )
A.
B.
C.
D.
5. 已知直线 : 与圆 : 交于 ,两点,则
的一个充分不必要条件是( )
A. B. C. D.
6. 一个直三棱柱形容器中盛有水,侧棱 ,底面 边 上的高为 .
当底面 水平放置时水面高度为 16(如图①).当侧面 水平放置时(如
图②),水面高度为( )
A. B. C. D.
7. 已知椭圆 的一条弦所在的直线方程是 弦的
中点坐标是 则椭圆的离心率是
A. B.
C. D.
8. 某校新闻社团负责报道采访本校田径运动会,社团派出甲、乙、丙、丁四名
成员到跳高、跳远、短跑三个比赛场地进行现场报道,且每个场地至少安排一人,
则甲不在短跑场地的不同安排的方法数为( )
A.12 B.18 C.24 D.32
二、多选题
9. 在 中,( )
A.若 ,则
B.若 ,则 为等腰三角形
C.若 ,则 为钝角三角形
D.若 是锐角, ,则 为锐角三角形
10. 已知 , 是 的共轭复数,则( )
A.若 ,则
B.若 为纯虚数,则
C.若 ,则
D.若 ,则集合 所构成区域的面积为
11. 已知函数 ,若关于 的方程 有四个
不同的根,它们从小到大依次记为 , , , ,则( )
A. B.
C. D.函数 有 6个零点
三、填空题
12. 如图为函数 的部分图
象,则 的值为_____
13. 在 的展开式中,各项系数之和为 ,则展开式中的常数项为
__________________.
14. 如图,一个圆环分成 , , , 四个区域,用 3种颜色(全部用完)对这
四个区域涂色,要求相邻区域不同色,则不同涂色的方法种数为____________.
(用数字作答)
四、解答题
15. 随着科技的进步,近年来,我国新能源汽车产业迅速发展,各大品牌新能源
汽车除了靠不断提高汽车的性能和质量来提升品牌竞争力,在广告投放方面的花
费也是逐年攀升.某校数学兴趣小组对某品牌新能源汽车近 5 年的广告费投入
(单位:亿元)进行了统计, 具体数据见下表:
年份代号 1 2 3 4 5
广告费投入 4.85.66. 27. 68. 8
并随机调查了 400 名市民对该品牌新能源汽车的认可情况,得到的部分数据见
下表:
认可不认可
50 岁以下 140 60
50 岁及以上 120 80
(1)求广告费投入 与年份代号 之间的线性经验回归方程;
(2)依据小概率值 的 独立性检验,能否认为市民的年龄与对该品牌新能
源汽车的认可度有关联
附: ① 经验回归方程 中, ;
② ,其中 .
0.1 0.05 0.01 0.005 0.001
2.7063.8416.6357.87910.828
16. 如图 1在直角梯形 中, , , , ,
E 是 AD 的中点,O 是 AC 与 BE 的交点,将 沿 BE 折起到图 2中 的
位置,得到四棱锥 .
(1)证明: 平面 ;
(2)当平面 平面 ,求平面 与平面 夹角的余弦值.
17. 已知函数 ( ).
(1)若 ,求函数 的极值;
(2)求证: .
18. 为响应国家促进消费的政策,某大型商场举办了“消费满减乐翻天”的优惠
活动,顾客消费满 800 元(含 800 元)可抽奖一次,抽奖方案有两种(顾客只能
选择其中的一种)
方案 1:从装有 5个红球,3个蓝球(形状、大小完全相同)的抽奖盒中,有放
回地依次摸出 3个球.每摸出 1次红球,立减 150 元,若 3次都摸到红球,则额
外再减 200 元(即总共减 650 元);
方案 2:从装有 5个红球,3个蓝球(形状、大小完全相同)的抽奖盒中,不放
回地依次摸出 3个球.中奖规则为:若摸出 3个红球,享受免单优惠;若摸出 2
个红球,则打 5折;其余情况无优惠.
(1)顾客 A 选择抽奖方案 2,已知他第一次摸出红球,求他能够享受优惠的概率;
(2)顾客 B 恰好消费了 800 元,
①若他选择抽奖方案 1,求他实付金额的分布列和期望(结果精确到 0.01);
②试从实付金额的期望值分析顾客 B 选择何种抽奖方案更合理.
19. 17 世纪荷兰数学家舒腾设计了多种圆锥曲线规,其中的一种如图 1所示.四
根等长的杆用铰链首尾链接,构成菱形 .带槽杆 长为 ,点 , 间
的距离为 2,转动杆 一周的过程中始终有 .点 M 在线段 的延
长线上,且 .
(1)建立如图 2所示的平面直角坐标系,求出点 E 的轨迹Γ的方程;
(2)过点 的直线 与Γ交于 A、B 两点.记直线 MA、MB 的斜率为 、 ,证明:
为定值.
云南省西双版纳傣族自治州景洪市曲靖一中景洪学校 2024-2025 学年高二下
学期期中检测数学试卷
整体难度:适中
考试范围:集合与常用逻辑用语、函数与导数、数列、空间向量与立体几何、平面解析几何、
计数原理与概率统计、三角函数与解三角形、复数
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
容易 2
较易 7
适中 9
较难 1
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.94 交并补混合运算
2 0.94 利用导数求函数的单调区间(不含参)
3 0.85 利用等差数列的性质计算
4 0.85 空间向量加减运算的几何表示;空间向量数乘运算的几何表示
判断命题的充分不必要条件;由直线与圆的位置关系求参数;求点到直线的距离;
5 0.65
圆的弦长与中点弦
6 0.85 柱体体积的有关计算
7 0.65 求椭圆的离心率或离心率的取值范围
分组分配问题;分类加法计数原理;分步乘法计数原理及简单应用;元素(位置)
8 0.65
有限制的排列问题
二、多选题
9 0.85 正弦定理解三角形;正、余弦定理判定三角形形状
复数的基本概念;与复数模相关的轨迹(图形)问题;共轭复数的概念及计算;
10 0.65
复数的除法运算
函数图象的应用;根据函数零点的个数求参数范围;函数与方程的综合应用;求
11 0.4
函数零点或方程根的个数
三、填空题
12 0.85 由图象确定正(余)弦型函数解析式
13 0.85 求指定项的系数;二项展开式各项的系数和
14 0.85 涂色问题
四、解答题
15 0.65 求回归直线方程;独立性检验解决实际问题
16 0.65 证明线面垂直;面面角的向量求法
17 0.65 求已知函数的极值;利用导数研究不等式恒成立问题;利用导数证明不等式
18 0.65 计算古典概型问题的概率;计算条件概率;超几何分布的均值;二项分布的均值
根据 a、b、c 求椭圆标准方程;根据韦达定理求参数;根据直线与椭圆的位置
19 0.65
关系求参数或范围;椭圆中的定值问题
知识点分析
序号 知识点 对应题号
1 集合与常用逻辑用语 1,5
2 函数与导数 2,11,17
3 数列 3
4 空间向量与立体几何 4,6,16
5 平面解析几何 5,7,19
6 计数原理与概率统计 8,13,14,15,18
7 三角函数与解三角形 9,12
8 复数 10
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
同课章节目录
