人教版九年级数学上册第二十二章 二次函数;二次函数的图象与系数的关系(40题)(举一反三专项训练)(含详解)
文档属性
| 名称 | 人教版九年级数学上册第二十二章 二次函数;二次函数的图象与系数的关系(40题)(举一反三专项训练)(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 711.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-30 15:19:47 | ||
图片预览




文档简介
专题01 二次函数的图象与系数的关系(举一反三专项训练)
【人教版】
考卷信息:
本套训练卷共40题,选择题25题,填空题15题.题型针对性较高,覆盖面广,选题有深度,可加强学生对二次函数图象与各项系数符号之间的关系的理解!
一、单选题(25题)
1.(2025·安徽·中考真题)已知二次函数的图象如图所示,则( )
A. B. C. D.
2.(2025·四川泸州·中考真题)已知抛物线的对称轴为直线,与轴的交点位于轴下方,且时,,下列结论正确的是( )
A. B. C. D.
3.(2025·黑龙江绥化·中考真题)如图,二次函数与轴交于点、,与轴交于点,其中.则下列结论:
①;②方程没有实数根;③; ④.
其中错误的个数有( )
A.1个 B.2个 C.3个 D.4个
4.(2025·四川遂宁·中考真题)如图,已知抛物线(为常数,且)的对称轴是直线,且抛物线与轴的一个交点坐标是,与轴交点坐标是且.有下列结论:①;②;③;④关于的一元二次方程必有两个不相等实根;⑤若点在抛物线上,且,当时,则的取值范围为.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
5.(2025·四川宜宾·中考真题)如图,是坐标原点,已知二次函数的图象与轴交于两点,与轴交于点,顶点为,对称轴为直线,其中,且.以下结论:①;②;③是钝角三角形;④若方程的两根为、,则,.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
6.(2025·山东烟台·中考真题)如图,二次函数的部分图象与轴的一个交点位于和之间,顶点的坐标为.下列结论:①;②对于任意实数,都有;③;④若该二次函数的图象与轴的另一个交点为,且是等边三角形,则.其中所有正确结论的序号是( )
A.①② B.①③ C.①④ D.①③④
7.(2025·黑龙江齐齐哈尔·中考真题)如图,二次函数的图象与轴交于两点,,且.下列结论:①;②;③;④若和是关于的一元二次方程 的两根,且,则,;⑤关于的不等式 的解集为.其中正确结论的个数是( )
A.2 B.3 C.4 D.5
8.(2025·四川广安·中考真题)如图,二次函数(a,b,c为常数,)的图象交x轴于A,B两点,点A的坐标是,点B的坐标是,有下列结论:①;②;③关于x的方程的解是,;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.(2025·四川达州·中考真题)如图,抛物线与x轴交于点,点,下列结论:①;②;③;④.正确的个数为( )
A.1个 B.2个 C.3个 D.4个
10.(2025·四川凉山·中考真题)二次函数的部分图像如图所示,其对称轴为,且图像经过点,则下列结论错误的是( )
A.
B.
C.若且,则
D.若两点都在抛物线的图像上,则
11.(2025·湖北十堰·模拟预测)抛物线(a为常数且),过点,且,下列结论:①;②;③;④若关于x的方程有实数根,则.其中正确的结论有( )
A.①③④ B.②③④ C.①②③ D.②④
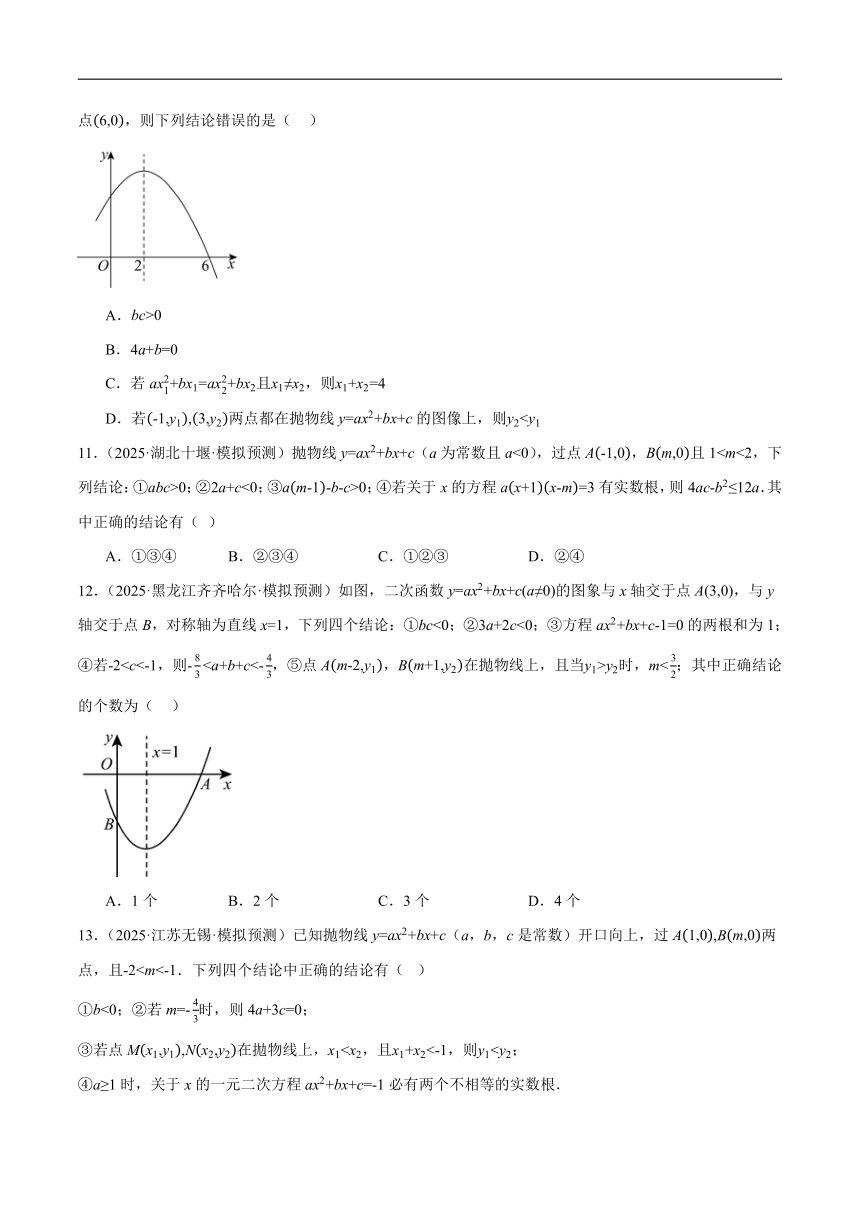
12.(2025·黑龙江齐齐哈尔·模拟预测)如图,二次函数的图象与x轴交于点,与y轴交于点B,对称轴为直线,下列四个结论:①;②;③方程的两根和为1;④若,则,⑤点,在抛物线上,且当时,;其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
13.(2025·江苏无锡·模拟预测)已知抛物线(a,b,c是常数)开口向上,过两点,且.下列四个结论中正确的结论有( )
①;②若时,则;
③若点在拋物线上,,且,则;
④时,关于x的一元二次方程必有两个不相等的实数根.
A.①③ B.②③ C.②④ D.③④
14.(2025·青海·三模)如图是抛物线图象的一部分,其顶点坐标为,与x轴的一个交点为,直线与抛物线交于A,B两点,下列结论:①;②;③抛物线与x轴的另一个交点是;④不等式的解集为;⑤方程有两个相等的实数根;其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
15.(2025·陕西西安·模拟预测)抛物线的对称轴为直线,与x轴的一个交点A在点和之间,其部分图象如图所示,以下结论正确的有( )
①;②;③若m为任意实数,则有;④点,在其图象上,若,且,则一定有.
A.1个 B.2个 C.3个 D.4个
16.(2025·黑龙江齐齐哈尔·三模)如图所示是二次函数的部分图象,该函数图象的对称轴是直线,图象与轴交点的纵坐标是.则下列结论:①;②方程一定有两个不相等的实数根:③当时,;④;⑤抛物线上有两点,,若,则.其中正确结论的个数有( )
A.个 B.个 C.个 D.个
17.(2025·湖北襄阳·模拟预测)已知抛物线(,,为常数,)经过点,开口向下,对称轴为直线.下列结论正确的是( )
A. B.
C. D.
18.(2025·贵州遵义·模拟预测)已知二次函数,其对称轴为.现有以下五个结论:①;②;③;④;⑤.其中正确的是________.
A.①②③④⑤ B.①③④⑤ C.②③④ D.①②⑤
19.(2025·福建福州·三模)已知抛物线与轴交于点,其中.以下四个结论:①;②;③函数的最小值大于;④不等式的解集为.其中正确结论的序号为( )
A.①② B.①③ C.②③ D.①④
20.(2025·浙江绍兴·三模)如图,二次函数的图象经过点,,与y轴交于点C.下列结论:①;②;③;④当时,y随x的增大而增大.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
21.(2025·贵州铜仁·三模)已知:二次函数的图象如图所示,下列结论中:①;②;③;④两根分别为,;⑤.其中正确的项有( )
A.2个 B.3个 C.4个 D.5个
22.(2025·贵州黔西·二模)如图为二次函数的部分图象,已知抛物线的对称轴为直线,若点的坐标为,则以下结论错误的是( )
A.方程的两根为,
B.8
C.
D.若,是抛物线上的两点,且,则
23.(2025·湖北·模拟预测)如图,已知抛物线为常数,且的对称轴为直线,且该抛物线与轴交于点,与轴的交点在,之间(不含端点),有下列结论:①;②;③;④若方程的两根为,,则.其中正确的个数为( )
A.4 B.3 C.2 D.1
24.(2025·江西新余·模拟预测)如图,已知二次函数的图象如图所示,其对称轴为直线,以下4个结论:①;②;③若点在该抛物线上,且,则;④.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
25.(2025·黑龙江齐齐哈尔·二模)如图所示是二次函数的部分图象,该函数图象的对称轴是直线,图象与轴交点的纵坐标是2.则下列结论:①;②方程一定有一个根在和之间;③方程一定有两个不相等的实数根;④点,在抛物线上,且,当时,;⑤函数的最大值大于.其中正确结论的个数为( )
A.5个 B.4个 C.3个 D.2个
二、填空题(15题)
26.(2025·四川绵阳·三模)已知二次函数的图象如图所示,根据已知信息有下列结论:①;②;③;④.其中正确的是 .
27.(2025·四川自贡·二模)如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下面五个结论正确的序号为 .
①; ②; ③;④;⑤时,
28.(2025·山东烟台·一模)已知抛物线(a,b,c均为常数,且)经过点,下列结论:①;②;③当时y随x的增大而增大;④关于x的方程有两个不相等的实数根.其中正确结论的个数是 个.
29.(2025·江苏淮安·二模)如图是二次函数图象的一部分,对称轴为,且经过点 .以下说法:①;②;③;④若是抛物线上的两点,则;⑤(其中),其中说法正确的是 .
30.(2025·江苏扬州·一模)如图,二次函数图像的对称轴是直线,下列结论:①;②;③(m为常数);④若关于x的方程恰有三个解,则,其中正确的是 (填序号).
31.(2025·湖北武汉·模拟预测)抛物线(是常数)经过点和两点,且.以下四个结论:①;②若,则;③若,则关于的一元二次方程必有两个相等的实数根;④点、在抛物线上,若,,总有,则.其中正确的是 (填写序号).
32.(2025·四川南充·一模)如图,二次函数的图象与x轴交于点,与y轴的交点B在与之间(不包括这两点),对称轴为直线.下列结论:①;②若点,点是函数图象上两点,则;③当时,将抛物线先向上平移4个单位,再向右平移1个单位,得到抛物线;④;⑤.
其中正确的有 (填序号)
33.(2025·湖北武汉·模拟预测)已知抛物线经过第四象限点,下列四个结论:①;②;③若抛物线经过点,则;④.其中正确的结论是 .(只填序号)
34.(2025·吉林长春·一模)如图,二次函数的图象与x轴交于、两点,与y轴交于点C,顶点为D,则下列结论:①;②;③若是等腰三角形,的值有2个;④当是直角三角形时.其中正确的是 .(只需填写序号)
35.(2025·湖北武汉·模拟预测)抛物线是常数,经过两点,且.
下列五个结论:
①;
②;
③若抛物线经过点,则;
④若关于的不等式的解集为,则;
⑤点在抛物线上,若,总有,则.
其中正确的结论是 (填写序号).
36.(24-25九年级上·广东珠海·期末)如图,抛物线与x轴交于A、B两点,与轴的正半轴交于点C,对称轴是直线,其顶点在第二象限,给出以下结论:①;②;③若,则;④不论m取任何实数,均有.其中正确的有 .
37.(2025·湖北武汉·模拟预测)抛物线(a,b,c是常数,)经过,两点,且,下列四个结论:
①;
②若,则关于x的一元二次方程没有实数解;
③点,在抛物线上上,若,,总有;
④若抛物线的顶点的轨迹上有两点,,则关于x的方程的两根之和大于1.
其中正确的是 (填写序号).
38.(24-25九年级上·北京西城·期末)如图,在平面直角坐标系中,已知点,其中,抛物线经过点和,以下四个结论:
①;②;③关于的一元二次方程无实根;④点,在抛物线上且在对称轴的同侧,当时,总有时,则.其中所有正确结论的序号是 .
39.(2025·湖北武汉·一模)开口向下的抛物线经过点,且.下列结论:①;②;③已知点在抛物线上,若,则;④若方程有两个不相等的实数根,则.其中正确结论的序号是 .
40.(24-25九年级上·湖北武汉·期中)已知抛物线(为常数,)经过点,,且,则下列四个结论:①;②;③若方程有两个不相等的实数根(且),则;④若,抛物线过点,且,则.其中正确的结论是 (填序号).
专题01 二次函数的图象与系数的关系(举一反三专项训练)
【人教版】
考卷信息:
本套训练卷共40题,选择题25题,填空题15题.题型针对性较高,覆盖面广,选题有深度,可加强学生对二次函数图象与各项系数符号之间的关系的理解!
一、单选题(25题)
1.(2025·安徽·中考真题)已知二次函数的图象如图所示,则( )
A. B. C. D.
【答案】C
【分析】根据二次函数图象的开口方向、对称轴位置、与轴交点及特殊点的函数值,结合二次函数性质,逐一分析选项 .本题主要考查了二次函数的图象与性质,熟练掌握二次函数中(开口方向)、(对称轴与共同决定)、(与轴交点)的意义及特殊点函数值的应用是解题的关键.
【详解】解: 二次函数图象中,开口向上,
.
对称轴,又,
,即.
抛物线与轴交点在负半轴,
.
选项A:,,,
两负一正相乘得正,
,该选项错误.
选项B:对称轴,由图象知对称轴,即,
又,两边乘得,,该选项错误.
选项C:当时,,即;当时,,
,该选项正确.
选项D:当时,,由图象知对应的函数值,
,该选项错误.
故选.
2.(2025·四川泸州·中考真题)已知抛物线的对称轴为直线,与轴的交点位于轴下方,且时,,下列结论正确的是( )
A. B. C. D.
【答案】D
【分析】本题主要考查了二次函数的图象与性质,二次函数与一元二次方程之间的关系,根据对称轴公式可得,即,据此可判断A;根据题意可得当时,,再由当时,,可得抛物线与轴的一个交点一定在直线和轴之间,则抛物线与轴的另一个交点一定在直线和直线之间,据此可判断B;当时,,再由,即可判断D;根据抛物线与轴的一个交点一定在直线和轴之间,当时,,根据题意不能确定的符号,则C选项不一定成立.
【详解】解:∵抛物线的对称轴为直线,
∴,
∴,故A选项中原结论错误,不符合题意;
∵抛物线与轴的交点位于轴下方,
∴当时,,
∵当时,,
∴抛物线与轴的一个交点一定在直线和轴之间,
∴抛物线与轴的另一个交点一定在直线和直线之间,
∴抛物线与轴有两个不同的交点,
∴关于的一元二次方程有两个不相同的实数根,
∴,故B选项中原结论错误,不符合题意;
∵当时,,且当时,,
∴抛物线开口向上,
∵抛物线与轴的另一个交点一定在直线和直线之间,
∴当时,,
∴,即,故D选项中原结论正确,符合题意;
当时,,
∵抛物线与轴的一个交点一定在直线和轴之间,
∴当时,的符号不确定,即的符号不确定,
∴不一定成立,故C选项不正确,不符合题意;
故选:D.
3.(2025·黑龙江绥化·中考真题)如图,二次函数与轴交于点、,与轴交于点,其中.则下列结论:
①;②方程没有实数根;③; ④.
其中错误的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】A
【分析】本题考查了二次函数图象的性质,掌握二次函数图象开口,对称轴直线,最值的计算方法是关键.
根据题意得到图象开口向上,对称轴直线为,,则,当时,代入计算可判定①;根据二次函数与直线的位置关系可判定②;根据题意得到,可判定③;根据函数最小值的大小可判定④;由此即可求解.
【详解】解:二次函数与轴交于点、,图象开口向上,
∴对称轴直线为,,
∴,
当时,,
∴,即,
∴,
∴,故①正确;
图象开口向上,对称轴直线为,
∴当时,函数有最小值,最小值轴的下方,
∴抛物线与直线两个不同的交点,
∴方程有两个不相等的实数根,故②错误;
∵二次函数与轴交于点,其中,
∴当,,
∴,
∵,
∴,
∴,
解得,,故③正确;
当时,函数有最小值,最小值为,,
∴,
∴,故④正确;
综上所述,正确的有①③④,错误的有②,
∴错误的有1个,
故选:A .
4.(2025·四川遂宁·中考真题)如图,已知抛物线(为常数,且)的对称轴是直线,且抛物线与轴的一个交点坐标是,与轴交点坐标是且.有下列结论:①;②;③;④关于的一元二次方程必有两个不相等实根;⑤若点在抛物线上,且,当时,则的取值范围为.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
【答案】C
【分析】本题考查了二次函数的图象与性质,一元二次方程根的判别式,熟练掌握以上知识点是解题的关键.根据函数图象结合二次函数的性质,先判断的符号即可判断①;进而根据对称性得出另一个交点坐标为,则当时,,即可判断②;根据,,结合抛物线的顶点坐标,即可判断③;求得的范围进而根据一元二次方程根的判别式判断一元二次方程的解情况即可判断④;根据,结合函数图象分析,即可得出,进而判断⑤,即可求解.
【详解】解:根据函数图象可得抛物线开口向下,则,对称轴为直线,则
∴ ,
又∵抛物线与轴交点坐标是,即,
∵,即,
∴,故①正确;
∵抛物线与轴的一个交点坐标是,对称轴为直线,
∴另一个交点坐标为,
∴当时,,故②错误;
∵,在抛物线的图象上,
∴,
又∵,
∴,
∴即,
∵,即,
∴,
∴即,
当时,取得最大值,最大值为,
∴,
∴,故③正确;
∵,,,
即,
∵
对称轴为直线,当时,的值随的增大而减小,
又∵,
∴,
∴当时,,
∴当时,恒成立,即必有两个不相等实根,故④正确;
∵若点在抛物线上,且,
∴,,
∵存在,
∴,,
即,,,
解得:,故⑤正确;
故正确的有①③④⑤,共4个.
故选:C.
5.(2025·四川宜宾·中考真题)如图,是坐标原点,已知二次函数的图象与轴交于两点,与轴交于点,顶点为,对称轴为直线,其中,且.以下结论:①;②;③是钝角三角形;④若方程的两根为、,则,.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】首先由抛物线开口向上得到,然后由对称轴得到,然后由抛物线与y轴交于负半轴得到,即可判断①;由对称轴为直线得到,然后将代入抛物线得到,代入得到,然后根据得到,即可判断②;设抛物线对称轴与x轴交于点E,将代入抛物线得到,求出,然后求出,得到,得到,即可判断③;分别将和代入方程,整理求出和或6,进而求解即可.
【详解】∵抛物线开口向上
∴
∵对称轴为直线
∴
∵抛物线与y轴交于负半轴
∴
∴,故①错误;
∵对称轴为直线
∴
∵在抛物线上
∴
∴
∴
∵
∴
∴,故②正确;
如图所示,设抛物线对称轴与x轴交于点E,
将代入
将,代入得,
∴
∵
∵对称轴为直线,
∴
∴
∴
∵
∴
∴
∴是钝角三角形,故③正确;
∵
∴当时,,
∴方程转化为
解得;
∴当时,,
∴方程转化为
解得或6;
∵方程的两根为、
∴,,故④正确.
综上所述,其中正确结论有3个.
故选:C.
【点睛】此题考查了二次函数的图象和性质,二次函数和x轴交点问题,解直角三角形,解一元二次方程等知识,解题的关键是掌握以上知识点.
6.(2025·山东烟台·中考真题)如图,二次函数的部分图象与轴的一个交点位于和之间,顶点的坐标为.下列结论:①;②对于任意实数,都有;③;④若该二次函数的图象与轴的另一个交点为,且是等边三角形,则.其中所有正确结论的序号是( )
A.①② B.①③ C.①④ D.①③④
【答案】D
【分析】由二次函数的图象的开口向下,与轴交于正半轴,对称轴在轴的右侧,,,,可得①符合题意;结合当时,最大,当时,,可得②不符合题意;由,,可得,可得③符合题意;由,记的横坐标分别为,可得,结合,可得,可得④符合题意.
【详解】解:∵二次函数的图象的开口向下,与轴交于正半轴,对称轴在轴的右侧,
∴,,,
∴,故①符合题意;
∵顶点的坐标为,
∴当时,最大,
当时,,
∴,
∴,故②不符合题意;
∵二次函数的部分图象与轴的一个交点位于和之间,对称轴为直线,
∴,,
∴,,
∴,故③符合题意;
如图,为等边三角形,
∴,,,,
∴,
记的横坐标分别为,
∴,
∴,
当,则,,
∴,
∴,
∵,
∴,
∴,
∴,
故④符合题意;
故选:D
【点睛】本题考查的是二次函数的图象与性质,等边三角形的性质,锐角三角函数的性质,熟练的利用等边三角形的性质结合二次函数的图象解题是关键.
7.(2025·黑龙江齐齐哈尔·中考真题)如图,二次函数的图象与轴交于两点,,且.下列结论:①;②;③;④若和是关于的一元二次方程 的两根,且,则,;⑤关于的不等式 的解集为.其中正确结论的个数是( )
A.2 B.3 C.4 D.5
【答案】B
【分析】本题考查了二次函数图象与性质,根据抛物线开口,对称轴,以及与轴的交点,确定的符号,即可判断①,根据二次函数的图象过,得出,进而判断对称轴,得出,进而判断②和③,根据函数图象判断④,将一般式写成交点式得出 ,化简不等式为,求得解集,即可求解.
【详解】解:∵抛物线开口向上,
∴,
∵对称轴在轴的右侧,
∴,
∴,
∵抛物线与轴交于负半轴,
∴,
∴,故①正确,
∵二次函数的图象过,
∴,
∵二次函数的图象与轴交于两点,,且.
∴对称轴,即,
∴,
∴,
∴,故②正确;
∵,
∴
,
∴,故③错误;
④如图,
关于的一元二次方程 的两个根,即函数与的交点的横坐标,
∵,
∴若和是关于的一元二次方程 的两根,且,则,;故④正确;
⑤∵二次函数的图象与轴交于两点,,
∴
,
∴,,
∴,,
∴可化为,
即,
∵,
∴,
解得:或,
∴关于的不等式 的解集为或不是故⑤错误
故正确的有①②④,共3个,
故选:B
8.(2025·四川广安·中考真题)如图,二次函数(a,b,c为常数,)的图象交x轴于A,B两点,点A的坐标是,点B的坐标是,有下列结论:①;②;③关于x的方程的解是,;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】本题考查了二次函数的图象与性质、抛物线与x轴的交点等知识,熟练掌握二次函数的图象与性质是解题的关键;
根据图象可得:抛物线的开口向下,交y轴于正半轴,即得,进而可判断,即可判断结论①;当时,,即,可判断结论②;根据二次函数与x轴的交点结合二次函数的对称性即可判断结论③④,可得答案.
【详解】解:根据图象可得:抛物线的开口向下,交y轴于正半轴,
∴,
又∵抛物线的对称轴在y轴右侧,
∴,
∴,
∴,故结论①正确;
由函数的图象可得:当时,,即,
即,故结论②错误;
∵二次函数的图象交x轴于A,B两点,点A,点B,
∴关于x的方程的解是,,,故结论③④正确;
综上,结论正确的有3个,
故选:C.
9.(2025·四川达州·中考真题)如图,抛物线与x轴交于点,点,下列结论:①;②;③;④.正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】本题考查了二次函数的图象和性质以及二次函数与一元二次方程的关系,熟练掌握二次函数的图象与性质是解题的关键;
根据抛物线开口向上,与y轴交于正半轴,可得,根据抛物线与x轴交于点,点,当时,即可逐一判断,进而求解.
【详解】解:∵抛物线开口向上,与y轴交于正半轴,
∴,
∵抛物线与x轴交于点,点,当时,
∴抛物线的对称轴是直线,,,
故结论③④正确;
∴,即,,
故结论②正确;
∴,
故结论①正确;
综上,说法正确的有4个;
故选:D.
10.(2025·四川凉山·中考真题)二次函数的部分图像如图所示,其对称轴为,且图像经过点,则下列结论错误的是( )
A.
B.
C.若且,则
D.若两点都在抛物线的图像上,则
【答案】D
【分析】本题考查二次函数的图像和性质,根据图像判断系数之间的关系,从图像获取信息,根据二次函数的对称性,增减性,逐一进行判断即可.
【详解】解:由图像可知,抛物线的开口向下,与轴交于正半轴,
∴,
∵对称轴为直线,
∴,
∴,,故选项A,B正确,不符合题意;
∵且,
∴,
∴和关于对称轴对称,
∴;故选项C正确;不符合题意;
∵抛物线的开口向下,
∴抛物线上的点离对称轴越远,函数值越小,
若两点都在抛物线的图像上,
∵,
∴;故选项D错误,符合题意;
故选D.
11.(2025·湖北十堰·模拟预测)抛物线(a为常数且),过点,且,下列结论:①;②;③;④若关于x的方程有实数根,则.其中正确的结论有( )
A.①③④ B.②③④ C.①②③ D.②④
【答案】D
【分析】本题考查了二次函数的图象与性质,二次函数与一元二次方程的关系.熟练掌握二次函数的图象与性质,二次函数与一元二次方程的关系是解题的关键.
根据及过点,且,结合二次函数的性质与判别式条件,逐一分析各结论的正确性.
【详解】解:①∵抛物线(a为常数且),过点,
∴抛物线可表示为,
∴,
∵
∴,
∴,
∴,结论①错误;
②将代入,得
∵,
∴,
∵,
∴,结论②正确;
③∵,
∴
∵
∴
∴
∵
∴,结论③错误;
④∵
∴
∴
∴
∴
∵,
∵,结论④正确.
综上,正确结论为②④,
故选:D.
12.(2025·黑龙江齐齐哈尔·模拟预测)如图,二次函数的图象与x轴交于点,与y轴交于点B,对称轴为直线,下列四个结论:①;②;③方程的两根和为1;④若,则,⑤点,在抛物线上,且当时,;其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】此题考查了二次函数的图象和性质,数形结合是解题的关键,利用开口方向和对称轴的位置即可判断①,利用对称轴和特殊点的函数值即可判断②由根与系数的关系可得出,由代入即可判断③,求出,进一步得到,又根据得到,即可判断④. ⑤当点和关于对称轴对称时,解得m,若点A和点B向左移动时结合对称轴左侧的递减性,以及即可得到m的取值范围.
【详解】解:①函数图象开口方向向上,
;
对称轴在轴右侧,
、异号,
,
∵抛物线与轴交点在轴负半轴,
,
,故①错误;
②二次函数的图象与轴交于点,与轴交于点,对称轴为直线,
时,,
,
,
,
,
∵,
,故②正确;
③设方程的两根为和,
∴,
,
∴,故③错误.
④,
∴根据抛物线与相应方程的根与系数的关系可得,
,
,
,
,
,
,
故④正确;
⑤点,在抛物线上,
当时,,解得,
∵,
∴,则⑤正确;
故选:C.
13.(2025·江苏无锡·模拟预测)已知抛物线(a,b,c是常数)开口向上,过两点,且.下列四个结论中正确的结论有( )
①;②若时,则;
③若点在拋物线上,,且,则;
④时,关于x的一元二次方程必有两个不相等的实数根.
A.①③ B.②③ C.②④ D.③④
【答案】C
【分析】本题考查了二次函数图象的性质,一元二次方程根与系数的关系,掌握二次函数图象的对称性,增减性,二次函数与轴的交点,一元二次方程根与系数的关系是解题的关键.
根据二次函数图象开口向上,即,对称轴直线为,且可判定①;根据二次函数对称轴直线的计算方法,图象过点的知识结合可判定②;根据题意可得点到对称轴的距离大于点到对称轴的距离,图象开口向下,由离对称轴越远值越小可判定③;根据二次函数图象的性质,一元二次方程根与系数的关系可判定④;由此即可求解.
【详解】解:抛物线(,,是常数)开口向上,
∴,
∵二次函数图象过两点,
∴对称轴直线为,
∵,
∴,
∴,故①错误;
若,则,
∴,
把代入抛物线解析式得,,
∴,
∴,故②正确;
∵对称轴直线为,且,
∴,
已知点,在抛物线上,,且,
∴,
∴点到对称轴的距离大于点到对称轴的距离,
∴,故③错误;
已知抛物线过两点,
∴设抛物线解析式为:,
令,整理得,,
∴,
∵,,
∴,
∴,
∴
∴,
∴关于的一元二次方程必有两个不相等的实数根,故④正确.
综上所述,正确的有②④,
故选:C.
14.(2025·青海·三模)如图是抛物线图象的一部分,其顶点坐标为,与x轴的一个交点为,直线与抛物线交于A,B两点,下列结论:①;②;③抛物线与x轴的另一个交点是;④不等式的解集为;⑤方程有两个相等的实数根;其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】由题意,,,可判断错误;观察对称轴即可判断正确;根据对称性求出抛物线与轴的另一个交点是可判断④错误;抛物线 图象与直线只有一个交点,方程有两个相等的实数根,故⑤正确.
【详解】∵抛物线开口向上,
∴,
∵抛物线交轴于负半轴,
∴,
∵对称轴在轴右边,
∴,
∴,
∴,故错误,
∵顶点坐标为,
∴,
∴,故②正确;
∵,对称轴为直线,
∴抛物线与轴的另一个交点是,故错误,
由题意:图象与直线交于,两点,
∴当时,即不等式的解集为,故④正确,
∵抛物线 图象与直线只有一个交点,
∴方程有两个相等的实数根,故⑤正确,
故选C.
【点睛】此题考查了二次函数的性质、二次函数与不等式,二次函数与一元二次方程等知识,解题的关键是灵活运用所学知识解决问题,学会利用数形结合的思想解决问题.
15.(2025·陕西西安·模拟预测)抛物线的对称轴为直线,与x轴的一个交点A在点和之间,其部分图象如图所示,以下结论正确的有( )
①;②;③若m为任意实数,则有;④点,在其图象上,若,且,则一定有.
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】本题考查了二次函数的图象和性质,根据二次函数对称轴和图象得出的符号,即可判断①;由时,,即可判断②;最值判断③;根据二次函数性质可判断④;掌握二次函数的图象和性质是解题的关键.
【详解】解:∵抛物线的对称轴为,
∴,
∴,
∵抛物线开口向下,
∴,
∴,
∵抛物线对称轴为,与轴的一个交点在点和之间,
∴抛物线与轴的另一个交点在点和之间,
∴抛物线与轴的交点在轴的正半轴上,
∴,
∴,故①正确;
∵抛物线与轴的另一个交点在点和之间,
∴时,,
即,
∵,
∴,故②正确;
∵抛物线的开口向下,对称轴为直线,
∴当时,函数值最大,
∴当m为任意实数时,则:,
∴,故③正确;
∵抛物线开口向下,图象上有两点和,对称轴为 ,,且,
∴点在对称轴右侧,
当时, 在抛物线的右侧,随的增大而减小,
∵,
∴,
当时,点到对称轴的距离为,点到对称轴的距离为,
∵,
∴,
又∵抛物线开口向下,抛物线上的点离对称轴的越近,函数值越大,
∴,
∴图象上有两点和,若,且,则一定有,
故④正确;
∴结论正确的有个,
故选:.
16.(2025·黑龙江齐齐哈尔·三模)如图所示是二次函数的部分图象,该函数图象的对称轴是直线,图象与轴交点的纵坐标是.则下列结论:①;②方程一定有两个不相等的实数根:③当时,;④;⑤抛物线上有两点,,若,则.其中正确结论的个数有( )
A.个 B.个 C.个 D.个
【答案】C
【分析】根据抛物线的对称轴可得,进而判断结论①,结合一元二次方程跟的判别式和抛物线的开口方向,可得,进而判断结论②,根据抛物线的增减性,函数值可判断结论③,根据抛物线的对称性得出抛物线与轴的另一个交点在和之间,结合函数值得出,进而判断结论④,根据抛物线的对称性得出点关于对称轴的对称点坐标为,结合抛物线的增减性即可得出时,,进而判断结论⑤,即可求解.
【详解】解:∵二次函数的对称轴为,
即,
∴,
∴,故①结论正确;
∵,
∴,
整理得,
则,
∵抛物线开口向下,
∴,
故,,
∴,
故方程一定有两个不相等的实数根,②结论正确;
∵,,
故抛物线的解析式为,
当时,,
当时,,
∵,
∴,
∵抛物线的对称轴是,故抛物线的最大值为;
当时,,
故当时,;即③结论正确;
根据图象可得:抛物线与轴的一个交点在和之间,抛物线的对称轴为,
故抛物线与轴的另一个交点在和之间,
当时,,
∵,,
∴,
∴,故④结论错误;
∵抛物线的对称轴为,
故点关于对称轴的对称点坐标为,
∵抛物线的开口向下,
故抛物线在对称轴的左侧,随的增大而增大,抛物线在对称轴的右侧,随的增大而减小,
若,
则,故⑤结论错误;
综上,结论正确的有①②③,有个.
故选:C.
【点睛】本题考查了二次函数的性质,抛物线与轴的交点问题,抛物线与轴的交点问题,二次函数图象与系数的关系,一元二次方程跟的判别式等.解题的关键是掌握二次函数的图象与性质.
17.(2025·湖北襄阳·模拟预测)已知抛物线(,,为常数,)经过点,开口向下,对称轴为直线.下列结论正确的是( )
A. B.
C. D.
【答案】D
【分析】本题考查了二次函数的图象与性质,二次函数的最值,二次函数的对称性,熟练掌握以上知识点是解题的关键.根据对称轴,可知,结合该抛物线过,可知,从而知道,判断出A;可知该抛物线与轴的另一个交点是,将其代入抛物线可判断C,根据抛物线与轴的交点个数,可判断B,从开口向下以及对称轴,可判断时,抛物线取得最大值,可判断D,从而得出答案.
【详解】解: 开口向下,
,
对称轴为直线,
,
,
过,对称轴为直线,
当时,,
,故C错误;
过,,
,
,
,
,
,故A错误;
过,,
,故B错误;
抛物线开口向下,对称轴为直线,
时,取最大值,
,
,故D正确;
故选:D.
18.(2025·贵州遵义·模拟预测)已知二次函数,其对称轴为.现有以下五个结论:①;②;③;④;⑤.其中正确的是________.
A.①②③④⑤ B.①③④⑤ C.②③④ D.①②⑤
【答案】B
【分析】根据抛物线的对称性,抛物线与x轴的交点,对称轴的两种表示方法,抛物线的增减性,最值等解答即可.
【详解】解:∵二次函数开口向上,
∴,
∵抛物线的图象与y轴的交点在负半轴上,
∴;
∵对称轴为直线,
∴,
∴,
∴,
故①正确;
∵,,
∴,,
∴,
故②错误;
∵抛物线的顶点在第四象限,
∴,
故③正确;
∵对称轴为直线,
∴,
∵,
∴,
∴,
故④正确;
∵对称轴为直线,
∴,
∴,
∴,
故⑤正确,
故选:B.
【点睛】本题考查了抛物线的对称性,抛物线的顶点坐标属性,根的判别式,抛物线与各项系数的符号关系,熟练掌握性质是解题的关键.
19.(2025·福建福州·三模)已知抛物线与轴交于点,其中.以下四个结论:①;②;③函数的最小值大于;④不等式的解集为.其中正确结论的序号为( )
A.①② B.①③ C.②③ D.①④
【答案】A
【分析】本题考查了二次函数的图象和性质,二次函数和一次函数的交点问题,利用数形结合的思想解决问题是关键.
根据题意画出函数大致图象,得到a、b同号,,可判断①结论;根据,得,可判断②结论;根据,二次函数最小值为,可判断③结论;根据函数与函数的交点为和,利用图象可判断④结论.
【详解】解:根据题意画出函数大致图象如下:
∵抛物线与轴交于点,其中,
∴抛物线开口向上,对称轴在之间,与y轴交点在负半轴,
∴a、b同号,,
∴,
∴①结论正确;
∵,
∴,
∴,
∴②结论正确;
,
∵,
∴,
∵,
∴当时,
,
∴③结论错误;
∵函数中,当时,,当时,,
∴函数与函数的交点为和,
∴不等式的解集为或,
∴④结论错误.
故选:A.
20.(2025·浙江绍兴·三模)如图,二次函数的图象经过点,,与y轴交于点C.下列结论:①;②;③;④当时,y随x的增大而增大.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】A
【分析】此题考查了二次函数的图象,二次函数图象与系数的关系,根据二次函数的图象判断式子的正负,正确理解二次函数的图象及性质是解题的关键.根据二次函数的图象及性质解答即可.
【详解】解:由图象可知,开口向下,与y轴交于正半轴,
∴,
∴,故①不正确;
∵二次函数的图象经过点,,
∴对称轴为直线,,
∴,,故②正确;
∴当时,图象有最高点,即函数最大值为,
∴当时,,
∴,故③不正确;
∵对称轴为直线,开口向下,
当时,y随x的增大而减小,
∴当时,y随x的增大而先增大后减小.故④不正确;
∴正确的为②,共1个,
故选:A.
21.(2025·贵州铜仁·三模)已知:二次函数的图象如图所示,下列结论中:①;②;③;④两根分别为,;⑤.其中正确的项有( )
A.2个 B.3个 C.4个 D.5个
【答案】B
【分析】本题主要考查了二次函数的图象与性质,牢记公式和数形结合是解题的关键.由抛物线开口向上知:,抛物线与轴的负半轴相交可知:,对称轴在轴的左侧可知:,即可判断①;根据对称轴为直线,得出,从而得出,即可判断②;由抛物线的性质可知,当时,有最小值,得出,即可判断③;根据抛物线的对称轴为, 且与轴的一个交点的横坐标为1, 得出另一个交点的横坐标为,即可判断④;根据当时,,得出,即可判断⑤.
【详解】解:①由抛物线开口向上知:,抛物线与轴的负半轴相交可知:,对称轴在轴的左侧可知:,
∴,故①正确;
②∵对称轴为直线,
∴,即,
∴,故②错误;
③由抛物线的性质可知,当时,有最小值,
∴,
即,故③正确;
④∵抛物线的对称轴为, 且与轴的一个交点的横坐标为1,
∴另一个交点的横坐标为,
∴方程的两根分别是1,,故④错误;
⑤由图像可得,当时,,即:,故⑤正确;
故正确选项有①③⑤共3个,
故选:B.
22.(2025·贵州黔西·二模)如图为二次函数的部分图象,已知抛物线的对称轴为直线,若点的坐标为,则以下结论错误的是( )
A.方程的两根为,
B.8
C.
D.若,是抛物线上的两点,且,则
【答案】B
【分析】此题考查二次函数的图象和性质以及二次函数与x轴交点,数形结合是解题的关键.
根据题意求出抛物线与x轴的另一个交点坐标为,即可判断A;首先由对称轴得到,然后将代入解析式得到,然后推出,根据,即可得到,进而判断B;然后由抛物线y轴交于正半轴得到,即可判断C;根据题意得到当时,y随x的增大而增大,即可判断D.
【详解】∵抛物线的对称轴为直线,若点的坐标为,
∴抛物线与x轴的另一个交点坐标为
∴方程的两根为,,故A正确;
∵抛物线的对称轴为直线,
∴
∴
将代入得,
∴将代入得,
∵抛物线开口向下
∴
∴,故B错误;
∵抛物线y轴交于正半轴
∴
∴,故C正确;
∵抛物线的对称轴为直线,开口向下
∴当时,y随x的增大而增大
∵若,是抛物线上的两点,且,
∴,故D正确.
故选:B.
23.(2025·湖北·模拟预测)如图,已知抛物线为常数,且的对称轴为直线,且该抛物线与轴交于点,与轴的交点在,之间(不含端点),有下列结论:①;②;③;④若方程的两根为,,则.其中正确的个数为( )
A.4 B.3 C.2 D.1
【答案】B
【分析】本题考查二次函数的图象与系数的关系,根与系数的关系,抛物线与x轴的交点,根据二次函数图象的开口方向、对称轴位置、与x轴的交点坐标、根与系数的关系等知识,逐个判断即可.
【详解】解:∵抛物线开口向上,
∴,
∵对称轴为直线,a、b同号,
∴,
∵抛物线与y轴的交点B在,之间,
∴,
∴,故①不正确;
∵对称轴为直线,且该抛物线与x轴交于点,
∴与x轴交于另一点,
∴当时,,故②正确;
由题意可得,方程的两个根为,
又∵,即,
∵,
∴,
因此,故③正确;
若方程的两根为,,即方程为:,则直线与抛物线的交点的横坐标为m,n,
∵直线过一、二、三象限,且过点,
∴直线与抛物线的交点在第一、第三象限,
由图象可知.故④正确;
综上所述,正确的结论有②③④,共3个,
故选:B.
24.(2025·江西新余·模拟预测)如图,已知二次函数的图象如图所示,其对称轴为直线,以下4个结论:①;②;③若点在该抛物线上,且,则;④.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】本题考查了二次函数的图像和性质,熟悉函数的图像和性质是解题关键.
利用二次函数的开口方向,对称轴的位置和与y轴的交点坐标即可求出①;令即可判断②;利用时函数值最大,即可判断③;令即可判断④.
【详解】①由图象可知:,
,故①正确;
②当时,,对称轴为直线,
∴当时,,
∴,故②正确;
③当时,y的值最大,此时,,
而当时,,
∴,
∴,
∴,即,
∵,
∴,
∴,故③正确;
④当时,,对称轴为直线
∴当时,,
∴,
∴,故④错误;
故选:C.
25.(2025·黑龙江齐齐哈尔·二模)如图所示是二次函数的部分图象,该函数图象的对称轴是直线,图象与轴交点的纵坐标是2.则下列结论:①;②方程一定有一个根在和之间;③方程一定有两个不相等的实数根;④点,在抛物线上,且,当时,;⑤函数的最大值大于.其中正确结论的个数为( )
A.5个 B.4个 C.3个 D.2个
【答案】B
【分析】本题考查抛物线与x轴的交点,根与系数的关系,二次函数的性质,二次函数图象上点的坐标特征,解题的关键是掌握二次函数的图象和性质,熟练运用数形结合的方法解决问题.根据二次函数的对称性,开口方向等来判断结论①②,根据二次函数与一元二次方程的关系来判断结论③,根据函数的增减性,函数值判断结论④⑤即可.
【详解】解:抛物线的对称轴为直线,
,
,即,故①正确;
抛物线的对称轴为直线,与x轴的一个交点的横坐标在2和3之间,
抛物线与x轴的另一个交点的横坐标在和0之间,
∴方程一定有一个根在和0之间,故②错误;
∵抛物线图象与轴交点的纵坐标是2,
,
,
,
令,得,
或,
,
,
∴方程一定有两个不相等的实数根,故③正确;
抛物线的开口向下,
抛物线上的点距离对称轴越远y值越小,距离对称轴越近y值越大,
,
,
,
,
,
点到对称轴的距离是,点到对称轴的距离是,
,故④正确;
如图,当时,,
,
,
,
当时,,
函数的最大值大于,故⑤正确,
综上所述,正确的结论有:①③④⑤,共4个,
故选:B.
二、填空题(15题)
26.(2025·四川绵阳·三模)已知二次函数的图象如图所示,根据已知信息有下列结论:①;②;③;④.其中正确的是 .
【答案】①②④
【分析】本题主要考查二次函数的图象及性质,做题时会用数形结合的思想进行思考,从而判断函数解析式中各系数关系的正负性是解题的关键.由二次函数的图象及性质,逐个结论进行判段,从而解答本题.
【详解】解:由抛物线的开口方向可知:,
由对称轴的位置,可知:,
不等式两边同时乘以得:,
可得:,,
结论①正确;②正确;
由,,可知:,
由抛物线与轴的交点可知:,
,
结论③错误;
由二次函数与一元二次方程的联系得,关于的方程有两个不相等的实数根,
,
,
由上可知,,,,
,,
,
结论④正确;
综上所述:①②④正确;
故答案为:①②④.
27.(2025·四川自贡·二模)如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下面五个结论正确的序号为 .
①; ②; ③;④;⑤时,
【答案】②③④⑤
【分析】此题主要考查图象与二次函数系数之间的关系,解题关键是注意掌握数形结合思想的应用.
根据对称轴位置及图象开口向上可判断出的符号,从而判断①;利用对称轴,可判断②;利用对称轴和开口向上,即可判断最小值,从而判断③的正误;由二次函数的性质即可判断④;由推出,,得到,即可得到,可判断⑤.
【详解】解:抛物线开口向上,
,
抛物线对称轴为直线,
,
,
,
抛物线与轴交于点在轴的负半轴,
,
,
故结论①错误;
二次函数的图象与轴交于点,对称轴为直线,抛物线与轴的另一个交点为,
,
故结论②正确;
,
,
,
,
,
故结论③正确;
对称轴为直线,
函数的最小值为,
,
,
故结论④正确;
,
,
,
,
,
,
,
,
故结论⑤正确;
综上所述,结论正确的是②③④⑤;
故答案为:②③④⑤.
28.(2025·山东烟台·一模)已知抛物线(a,b,c均为常数,且)经过点,下列结论:①;②;③当时y随x的增大而增大;④关于x的方程有两个不相等的实数根.其中正确结论的个数是 个.
【答案】4
【分析】本题考查的是二次函数图象与系数的关系、一元二次方程根的判别式、抛物线与轴的交点,熟记二次函数的对称轴、增减性以及一元二次方程根的判别式是解题的关键.根据抛物线经过点、结合题意判断①②;根据抛物线的对称性判断③;根据一元二次方程根的判别式判断④.
【详解】解:②∵抛物线经过点,
∴,
∵,
∴,即,故②正确;
①∵,,
∴,
∴,故①正确;
③∵
∴对称轴,
∴当时,随的增大而增大,故③正确;
④∵,
∴,
对于方程,,
∴方程有两个不相等的实数根,故④正确;
综上所述,其中正确结论的个数是4.
故答案为:4.
29.(2025·江苏淮安·二模)如图是二次函数图象的一部分,对称轴为,且经过点 .以下说法:①;②;③;④若是抛物线上的两点,则;⑤(其中),其中说法正确的是 .
【答案】①②③④⑤
【分析】本题考查了二次函数图象与系数的关系:二次项系数a决定抛物线的开口方向和大小.当时,抛物线向上开口;当时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时,对称轴在y轴左;当a与b异号时,对称轴在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于抛物线与x轴交点个数由判别式确定:时,抛物线与x轴有2个交点;时,抛物线与x轴有1个交点;时,抛物线与x轴没有交点.
利用抛物线开口方向得到,利用抛物线的对称轴方程得到,利用抛物线与y轴的交点在x轴上方得到,则可对①进行判断;利用抛物线经过点得到,则可对③进行判断;同时得到,加上,则可对②进行判断;通过比较点到直线的距离与点到直线的距离的大小可对④进行判断;利用时,函数值最大以及可对⑤进行判断.
【详解】解:抛物线开口向下,
,
抛物线的对称轴为直线,
,
抛物线与y轴的交点在x轴上方,
,
,所以①正确;
抛物线经过点,
,所以③正确;
,
,所以②正确;
点到直线的距离比点到直线的距离大,
;所以④正确;
抛物线的对称轴为直线
当时,函数值最大,
,
,
即,所以⑤正确.
故答案为:①②③④⑤.
30.(2025·江苏扬州·一模)如图,二次函数图像的对称轴是直线,下列结论:①;②;③(m为常数);④若关于x的方程恰有三个解,则,其中正确的是 (填序号).
【答案】①②③④
【分析】本题考查根据二次函数的图象判断式子符号,二次函数图象与各项系数符号.熟练掌握二次函数的图象和性质是解题关键.
根据二次函数的图象和性质逐项判断即可.
【详解】解:由二次函数图象可知,
∵该二次函数对称轴为,
∴,
∴,
∴,故①正确;
由图象可知,当时,,即.
∵,
∴,故②正确;
当时,y取得最小值,
∴,即,故③正确;
当时,,
∴顶点坐标为,
根据题意得,
即将位于x轴下方的图像向上翻折,
∴翻折后的顶点坐标为,
∵若关于x的方程恰有三个解,
∴即函数与恰有三个解,
即恰好经过向上翻折后的图像的顶点,
∴,
∵,
代入得到,则,
故④正确;
综上可知正确的结论为①②③④,
故答案为:①②③④.
31.(2025·湖北武汉·模拟预测)抛物线(是常数)经过点和两点,且.以下四个结论:①;②若,则;③若,则关于的一元二次方程必有两个相等的实数根;④点、在抛物线上,若,,总有,则.其中正确的是 (填写序号).
【答案】①②
【分析】本题考查二次函数与方程、不等式的关系,二次函数的图象与性质,根据抛物线经过点和两点得到对称轴为直线,,再据此逐个分析即可.
【详解】解:∵抛物线(是常数)经过点和两点,且,
∴对称轴为直线,
∴,
∴,
故①正确;
∵抛物线(是常数)经过点和两点,且,
∴方程的解集为或,
∴不等式的解集为或,
∴不等式解集为或,
解得或,
∴若,则;
故②正确;
∵抛物线经过点,
∴,
∵,
∴,
∴关于的一元二次方程的判别式,
∴关于的一元二次方程必有两个实数根,但是不一定是相等实数根,
故③错误;
∵抛物线对称轴为直线,,
∴在对称轴右边随的增大而增大,
∵若,总有,
∴总在对称轴右边,
∴,
∵,
∴,
解得,
∵,
∴,
故④错误;
综上所述,正确的有①②,
故答案为:①②.
32.(2025·四川南充·一模)如图,二次函数的图象与x轴交于点,与y轴的交点B在与之间(不包括这两点),对称轴为直线.下列结论:①;②若点,点是函数图象上两点,则;③当时,将抛物线先向上平移4个单位,再向右平移1个单位,得到抛物线;④;⑤.
其中正确的有 (填序号)
【答案】①④⑤
【分析】根据二次函数图象的开口方向,对称轴的位置,与y轴交点的位置判断①符合题意;根据点N坐标和二次函数的对称轴确定二次函数图象过点,再根据二次函数的增减性即可判断②不符合题意;使用待定系数法求出抛物线解析式,再根据二次函数图象平移规律即可判断③不符合题意;把点A坐标和点A关于对称轴对称的点的坐标代入二次函数解析式,然后用a表示c,再根据点C的位置和不等式的性质即可判断④符合题意;根据二次函数的最值得到不等式,再根据不等式的性质和等价代换思想即可判断⑤符合题意.
【详解】解:∵二次函数图象开口方向向下,对称轴在y轴右侧,与y轴的交点在y轴的正半轴,
∴,,.
∴.
∴.故①符合题意.
∵点是函数图象上一点,对称轴是直线,
∴二次函数图象经过点.
∵二次函数图象开口方向向下,
∴当时,y随x的增大而增大.
∵函数图象上一点,
∴.故②不符合题意.
∵,二次函数图象对称轴是直线,
∴设二次函数解析式为.
把点坐标代入二次函数解析式得.
解得.
∴二次函数解析式为.
∴抛物线先向上平移4个单位,再向右平移1个单位得到抛物线为.故③不符合题意.
∵二次函数图象过点,二次函数对称轴是直线,
∴二次函数图象过点.
把点和代入二次函数解析式中得
用a来表示b和c得
∵二次函数图象与y轴的交点B在与之间(不包括这两点),
∴.
∴.
∴.故④符合题意.
∵二次函数图象开口方向向下,对称轴为直线,
∴二次函数在时取得最大值.
∴当时,,即.
∴.
∵,
∴.
∴.
∴.故⑤符合题意.
故①④⑤符合题意.
故答案为:①④⑤.
【点睛】本题考查二次函数的图象与系数关系,二次函数的对称性,二次函数的增减性,二次函数图象平移规律,待定系数法求二次函数解析式,二次函数的最值,不等式的性质,综合应用这些知识点是解题关键.
33.(2025·湖北武汉·模拟预测)已知抛物线经过第四象限点,下列四个结论:①;②;③若抛物线经过点,则;④.其中正确的结论是 .(只填序号)
【答案】①②③④
【分析】本题主要考查了二次函数的图像和性质,不等式的性质,根据点所在象限可得出,由二次函数的图像和性质得出,即,结合已知条件可判断①,把变形成即可判断②, 把代入二次函数解析得出,结合即可判断③,利用不等式的性质即可得出判断④.
【详解】解:∵点在第四象限,
∴,
把代入,即,
∵,
∴
∴,故①正确,
∴,
∴,
由可得出,
∴,即恒成立,故②正确,
若抛物线经过点,
∴,
∵,
∴,
∴,则,故③正确,
∵,,
∴,
∴可变形为:,
即,
整理得:,
∵,
∴
∴,显然成立,故④成立,
故答案为:①②③④
34.(2025·吉林长春·一模)如图,二次函数的图象与x轴交于、两点,与y轴交于点C,顶点为D,则下列结论:①;②;③若是等腰三角形,的值有2个;④当是直角三角形时.其中正确的是 .(只需填写序号)
【答案】①②③
【分析】由图象可得对称轴为直线,可得,可判断①;将点A坐标代入解析式可得,可判断②;由等腰三角形的性质和两点距离公式,可求a的值,可判断③;由直角三角形的性质和两点距离可求或,可判断④,即可求解.
【详解】解:∵二次函数的图象与x轴交于、两点,
∴对称轴为直线,
∴,
∴,
故①正确,
当时,,
∴,
∴,
∴,
故②正确;
∵二次函数,
∴点,
∴,,
当时,,
∴(正数值已舍去),
当时,,
∴(正数值已舍去),
∴当是等腰三角形时,a的值有2个,
故③正确;
∵二次函数,
∴顶点,
∴,,,
若,可得,
∴,
∴,
若,可得,
∴,
∴,
∴当是直角三角形时,或,
故④错误.
故答案为:①②③.
【点睛】本题考查了抛物线与x轴的交点,二次函数图象与系数关系,等腰三角形的性质,直角三角形的性质等知识,灵活运用这些性质进行推理是本题的关键.
35.(2025·湖北武汉·模拟预测)抛物线是常数,经过两点,且.
下列五个结论:
①;
②;
③若抛物线经过点,则;
④若关于的不等式的解集为,则;
⑤点在抛物线上,若,总有,则.
其中正确的结论是 (填写序号).
【答案】①③⑤
【分析】根据抛物线的对称性,增减性,对称轴的两种表示方法,抛物线与不等式,解答即可.
【详解】解:∵抛物线是常数,经过两点,且.
∴,,,
∴,
∴;
故①正确;
∵抛物线是常数,经过两点,且.
∴是方程的两个不相等的实数根,
∴;
故②错误;
∵抛物线经过点,
∴,
∵,
解得,
∵,
∴,
∴;
∴;
解得,
故③正确;
∵关于的不等式的解集为,
∴,
∴的两个根为,,
∵关于的不等式的解集为,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
故④错误;
∵点在抛物线上,抛物线的对称轴为,,总有,
∴,且,
解得,
∵
∴.
故⑤ 正确,
故答案为:①③⑤.
【点睛】本题考查了抛物线的对称性,抛物线与不等式,对称轴的两种表示方法,抛物线的增减性,熟练掌握性质是解题的关键.
36.(24-25九年级上·广东珠海·期末)如图,抛物线与x轴交于A、B两点,与轴的正半轴交于点C,对称轴是直线,其顶点在第二象限,给出以下结论:①;②;③若,则;④不论m取任何实数,均有.其中正确的有 .
【答案】①②③
【分析】本题主要考查了二次函数与系数的关系、二次函数图像上点的坐标特征及抛物线与轴的交点,根据所给函数图像,得出,,的符号,再结合抛物线的对称性及增减性对所给结论依次进行判断即可.熟知二次函数的图像与性质是解题的关键.
【详解】解:由所给图像可知,
,,,
所以.
故①正确.
因为抛物线的对称轴为直线,
所以,
则.
故②正确.
因为点坐标为,
由得,,
所以点的坐标为,
则,
所以.
因为抛物线的对称轴为直线,且点坐标为,
所以点的坐标为.
由得,
,
所以.
故③正确.
因为抛物线的对称轴为直线,且开口向下,
所以当时,二次函数有最大值,
即对于抛物线上的任意一点(横坐标为,总有,即.
故④错误.
故答案为:①②③.
37.(2025·湖北武汉·模拟预测)抛物线(a,b,c是常数,)经过,两点,且,下列四个结论:
①;
②若,则关于x的一元二次方程没有实数解;
③点,在抛物线上上,若,,总有;
④若抛物线的顶点的轨迹上有两点,,则关于x的方程的两根之和大于1.
其中正确的是 (填写序号).
【答案】①②④
【分析】根据抛物线(a,b,c是常数,)经过,两点,得出抛物线的对称轴为直线:,根据,得出即可判断①根据抛物线(a,b,c是常数,)经过,得出,根据,,得出,求出,得出,说明关于x的一元二次方程没有实数解,可判断②,根据抛物线的对称轴为:直线,设抛物线的对称轴为直线,得出,根据点,在抛物线上上,,,,分三种情况:当点,都在对称轴右侧时,当点,在对称轴两侧时,点在对称轴的左侧,即可判断③;先求出抛物线的顶点坐标在函数的图象上,根据,得出,根据抛物线的开口向下,对称轴为直线,得出在对称轴的右侧y随x的增大而减小,根据根与系数的关系即可判断④.
【详解】解:∵抛物线(a,b,c是常数,)经过,两点,且,
∴抛物线的对称轴为直线:,
,
∴,即,
∵,
∴,故①正确;
∵抛物线(a,b,c是常数,)经过,
∴,
∵,,
∴,
∴,
∵,
∴,
当时,一元二次方程为,
整理得:,
∵,
∴关于x的一元二次方程没有实数解,故②正确;
抛物线的对称轴为:
直线,
∵,
∴,
设抛物线的对称轴为直线,
∴,
∵点,在抛物线上上,,,,
∴当点,都在对称轴右侧时,,
当点,在对称轴两侧时,点关于对称轴的对称点为,
∵,
∴,
∴,
∵,,
∴点不可能都在对称轴的左侧,
综上分析可知:点,在抛物线上上,,时,,故③错误;
∵抛物线(a,b,c是常数,)经过,两点,
∴顶点坐标的横坐标为,,
顶点坐标的纵坐标为,
∴,
∵,
∴,
∴顶点坐标的横坐标,
把代入顶点坐标的纵坐标,
∵顶点坐标的横坐标为,
∴,
把代入得:,
∴抛物线的顶点坐标在函数的图象上,
∵,
∴,
∴抛物线的开口向下,对称轴为直线,
∴在对称轴的右侧y随x的增大而减小,
∵抛物线的顶点的轨迹上有两点,,
∴,,,
∴,
∴关于x的方程的两根之和,故④正确.
综上所述,①②④正确.
故答案为:①②④.
【点睛】本题主要考查二次函数图象与系数的关系,解题关键是掌握二次函数的性质,掌握二次函数与方程及不等式的关系.
38.(24-25九年级上·北京西城·期末)如图,在平面直角坐标系中,已知点,其中,抛物线经过点和,以下四个结论:
①;②;③关于的一元二次方程无实根;④点,在抛物线上且在对称轴的同侧,当时,总有时,则.其中所有正确结论的序号是 .
【答案】②④
【分析】本题主要考查了二次函数的图象与性质,抛物线上点的坐标的特征,对称轴,数形结合法,抛物线与轴的交点,二次函数与一元二次方程的联系,一元二次方程的根的判别式,熟练掌握二次函数的性质和二次函数与一元二次方程的联系是解题的关键.
①根据题中二次函数的图像判断开口方向,,以及抛物线与轴的交点,可判断的符号,进而可判断;
②由二次函数的图象知:当时,,;当时,,两式相加,化简可得
③一元二次方程的判别式 ,结合的关系与符号,进而可判断;
④设,且在对称轴右侧(在左侧同理),则,
,结合的关系与符号,进而可判断.
【详解】通过读图:
①因为,所以抛物线开口向上,
对称轴,由于,即对称轴,
可得,
抛物线与轴交于负半轴,所以,
综上,,结论①错误;
②: 二次函数的图象与轴交于由图可知,
又 ,
,
由二次函数的图象可知:
当时, ,
当时,,
两式相加,化简可得,结论②正确;
③一元二次方程的判别式 ,
因为,所以,
由,可得,所以 ,方程有两个不相等的实根,
结论③错误;
④设,且在对称轴右侧(在左侧同理),
则,
,
,
,
,
,
,
(在对称轴右侧),
,
又 ,
,
即 ,结论④正确.
综上,正确结论的序号是:②④.
39.(2025·湖北武汉·一模)开口向下的抛物线经过点,且.下列结论:①;②;③已知点在抛物线上,若,则;④若方程有两个不相等的实数根,则.其中正确结论的序号是 .
【答案】②④/④②
【分析】本题考查了二次函数的图象和性质,由题意可得抛物线的对称轴为直线,进而由得,得到,即可判断①;由抛物线经过点,得,得,即得,又由对称轴得,可得,即可得,即可判断②;利用二次函数的性质可判断③;由方程有两个不相等的实数根,可得抛物线与轴有两个不同的交点,根据根的判别式可判断④;综上即可求解,掌握二次函数的图象和性质是解题的关键.
【详解】解:∵抛物线经过点,
∴抛物线的对称轴为直线,
∵,
∴,即,
∴,
∵抛物线开口向下,
∴,
∴,故①错误;
∵抛物线经过点,
∴ ,
∴,
∴,
∵,
∴,
即,
∴,
∴,
∴,故②正确;
∵对称轴,抛物线开口向下,
∴当时,随的增大而增大,
∵,
∴,故③错误;
∵方程有两个不相等的实数根,
∴抛物线与轴有两个不同的交点,
即抛物线与轴有两个不同的交点,
∴,
∴,故④正确;
综上,正确结论的是②④,
故答案为:②④.
40.(24-25九年级上·湖北武汉·期中)已知抛物线(为常数,)经过点,,且,则下列四个结论:①;②;③若方程有两个不相等的实数根(且),则;④若,抛物线过点,且,则.其中正确的结论是 (填序号).
【答案】①②④
【分析】本题考查二次函数符号判断,根据得到抛物线过,再结合已知条件画出大致的函数图象,然后根据函数图象分析计算即可.
【详解】解:∵,
∴过,
∵,过点,,
∴函数的大致图象如下两种情况:
由函数图象可得,故①正确;
由函数图象可得当时,,
∵,
∴,
∴,
故②正确;
方程有两个不相等的实数根(且),可以看成抛物线与交点横坐标为,
有函数图象可得:当时,;当时,;
故③错误;
∵抛物线过点,
∴,
∴,整理得,,
∴,
∵抛物线过点,,
∴抛物线对称轴为直线,
∵,
∴,即,
∵,
∴解得,
∴,
故④正确;
综上所述,正确的有①②④,
故答案为:①②④.
【人教版】
考卷信息:
本套训练卷共40题,选择题25题,填空题15题.题型针对性较高,覆盖面广,选题有深度,可加强学生对二次函数图象与各项系数符号之间的关系的理解!
一、单选题(25题)
1.(2025·安徽·中考真题)已知二次函数的图象如图所示,则( )
A. B. C. D.
2.(2025·四川泸州·中考真题)已知抛物线的对称轴为直线,与轴的交点位于轴下方,且时,,下列结论正确的是( )
A. B. C. D.
3.(2025·黑龙江绥化·中考真题)如图,二次函数与轴交于点、,与轴交于点,其中.则下列结论:
①;②方程没有实数根;③; ④.
其中错误的个数有( )
A.1个 B.2个 C.3个 D.4个
4.(2025·四川遂宁·中考真题)如图,已知抛物线(为常数,且)的对称轴是直线,且抛物线与轴的一个交点坐标是,与轴交点坐标是且.有下列结论:①;②;③;④关于的一元二次方程必有两个不相等实根;⑤若点在抛物线上,且,当时,则的取值范围为.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
5.(2025·四川宜宾·中考真题)如图,是坐标原点,已知二次函数的图象与轴交于两点,与轴交于点,顶点为,对称轴为直线,其中,且.以下结论:①;②;③是钝角三角形;④若方程的两根为、,则,.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
6.(2025·山东烟台·中考真题)如图,二次函数的部分图象与轴的一个交点位于和之间,顶点的坐标为.下列结论:①;②对于任意实数,都有;③;④若该二次函数的图象与轴的另一个交点为,且是等边三角形,则.其中所有正确结论的序号是( )
A.①② B.①③ C.①④ D.①③④
7.(2025·黑龙江齐齐哈尔·中考真题)如图,二次函数的图象与轴交于两点,,且.下列结论:①;②;③;④若和是关于的一元二次方程 的两根,且,则,;⑤关于的不等式 的解集为.其中正确结论的个数是( )
A.2 B.3 C.4 D.5
8.(2025·四川广安·中考真题)如图,二次函数(a,b,c为常数,)的图象交x轴于A,B两点,点A的坐标是,点B的坐标是,有下列结论:①;②;③关于x的方程的解是,;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.(2025·四川达州·中考真题)如图,抛物线与x轴交于点,点,下列结论:①;②;③;④.正确的个数为( )
A.1个 B.2个 C.3个 D.4个
10.(2025·四川凉山·中考真题)二次函数的部分图像如图所示,其对称轴为,且图像经过点,则下列结论错误的是( )
A.
B.
C.若且,则
D.若两点都在抛物线的图像上,则
11.(2025·湖北十堰·模拟预测)抛物线(a为常数且),过点,且,下列结论:①;②;③;④若关于x的方程有实数根,则.其中正确的结论有( )
A.①③④ B.②③④ C.①②③ D.②④
12.(2025·黑龙江齐齐哈尔·模拟预测)如图,二次函数的图象与x轴交于点,与y轴交于点B,对称轴为直线,下列四个结论:①;②;③方程的两根和为1;④若,则,⑤点,在抛物线上,且当时,;其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
13.(2025·江苏无锡·模拟预测)已知抛物线(a,b,c是常数)开口向上,过两点,且.下列四个结论中正确的结论有( )
①;②若时,则;
③若点在拋物线上,,且,则;
④时,关于x的一元二次方程必有两个不相等的实数根.
A.①③ B.②③ C.②④ D.③④
14.(2025·青海·三模)如图是抛物线图象的一部分,其顶点坐标为,与x轴的一个交点为,直线与抛物线交于A,B两点,下列结论:①;②;③抛物线与x轴的另一个交点是;④不等式的解集为;⑤方程有两个相等的实数根;其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
15.(2025·陕西西安·模拟预测)抛物线的对称轴为直线,与x轴的一个交点A在点和之间,其部分图象如图所示,以下结论正确的有( )
①;②;③若m为任意实数,则有;④点,在其图象上,若,且,则一定有.
A.1个 B.2个 C.3个 D.4个
16.(2025·黑龙江齐齐哈尔·三模)如图所示是二次函数的部分图象,该函数图象的对称轴是直线,图象与轴交点的纵坐标是.则下列结论:①;②方程一定有两个不相等的实数根:③当时,;④;⑤抛物线上有两点,,若,则.其中正确结论的个数有( )
A.个 B.个 C.个 D.个
17.(2025·湖北襄阳·模拟预测)已知抛物线(,,为常数,)经过点,开口向下,对称轴为直线.下列结论正确的是( )
A. B.
C. D.
18.(2025·贵州遵义·模拟预测)已知二次函数,其对称轴为.现有以下五个结论:①;②;③;④;⑤.其中正确的是________.
A.①②③④⑤ B.①③④⑤ C.②③④ D.①②⑤
19.(2025·福建福州·三模)已知抛物线与轴交于点,其中.以下四个结论:①;②;③函数的最小值大于;④不等式的解集为.其中正确结论的序号为( )
A.①② B.①③ C.②③ D.①④
20.(2025·浙江绍兴·三模)如图,二次函数的图象经过点,,与y轴交于点C.下列结论:①;②;③;④当时,y随x的增大而增大.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
21.(2025·贵州铜仁·三模)已知:二次函数的图象如图所示,下列结论中:①;②;③;④两根分别为,;⑤.其中正确的项有( )
A.2个 B.3个 C.4个 D.5个
22.(2025·贵州黔西·二模)如图为二次函数的部分图象,已知抛物线的对称轴为直线,若点的坐标为,则以下结论错误的是( )
A.方程的两根为,
B.8
C.
D.若,是抛物线上的两点,且,则
23.(2025·湖北·模拟预测)如图,已知抛物线为常数,且的对称轴为直线,且该抛物线与轴交于点,与轴的交点在,之间(不含端点),有下列结论:①;②;③;④若方程的两根为,,则.其中正确的个数为( )
A.4 B.3 C.2 D.1
24.(2025·江西新余·模拟预测)如图,已知二次函数的图象如图所示,其对称轴为直线,以下4个结论:①;②;③若点在该抛物线上,且,则;④.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
25.(2025·黑龙江齐齐哈尔·二模)如图所示是二次函数的部分图象,该函数图象的对称轴是直线,图象与轴交点的纵坐标是2.则下列结论:①;②方程一定有一个根在和之间;③方程一定有两个不相等的实数根;④点,在抛物线上,且,当时,;⑤函数的最大值大于.其中正确结论的个数为( )
A.5个 B.4个 C.3个 D.2个
二、填空题(15题)
26.(2025·四川绵阳·三模)已知二次函数的图象如图所示,根据已知信息有下列结论:①;②;③;④.其中正确的是 .
27.(2025·四川自贡·二模)如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下面五个结论正确的序号为 .
①; ②; ③;④;⑤时,
28.(2025·山东烟台·一模)已知抛物线(a,b,c均为常数,且)经过点,下列结论:①;②;③当时y随x的增大而增大;④关于x的方程有两个不相等的实数根.其中正确结论的个数是 个.
29.(2025·江苏淮安·二模)如图是二次函数图象的一部分,对称轴为,且经过点 .以下说法:①;②;③;④若是抛物线上的两点,则;⑤(其中),其中说法正确的是 .
30.(2025·江苏扬州·一模)如图,二次函数图像的对称轴是直线,下列结论:①;②;③(m为常数);④若关于x的方程恰有三个解,则,其中正确的是 (填序号).
31.(2025·湖北武汉·模拟预测)抛物线(是常数)经过点和两点,且.以下四个结论:①;②若,则;③若,则关于的一元二次方程必有两个相等的实数根;④点、在抛物线上,若,,总有,则.其中正确的是 (填写序号).
32.(2025·四川南充·一模)如图,二次函数的图象与x轴交于点,与y轴的交点B在与之间(不包括这两点),对称轴为直线.下列结论:①;②若点,点是函数图象上两点,则;③当时,将抛物线先向上平移4个单位,再向右平移1个单位,得到抛物线;④;⑤.
其中正确的有 (填序号)
33.(2025·湖北武汉·模拟预测)已知抛物线经过第四象限点,下列四个结论:①;②;③若抛物线经过点,则;④.其中正确的结论是 .(只填序号)
34.(2025·吉林长春·一模)如图,二次函数的图象与x轴交于、两点,与y轴交于点C,顶点为D,则下列结论:①;②;③若是等腰三角形,的值有2个;④当是直角三角形时.其中正确的是 .(只需填写序号)
35.(2025·湖北武汉·模拟预测)抛物线是常数,经过两点,且.
下列五个结论:
①;
②;
③若抛物线经过点,则;
④若关于的不等式的解集为,则;
⑤点在抛物线上,若,总有,则.
其中正确的结论是 (填写序号).
36.(24-25九年级上·广东珠海·期末)如图,抛物线与x轴交于A、B两点,与轴的正半轴交于点C,对称轴是直线,其顶点在第二象限,给出以下结论:①;②;③若,则;④不论m取任何实数,均有.其中正确的有 .
37.(2025·湖北武汉·模拟预测)抛物线(a,b,c是常数,)经过,两点,且,下列四个结论:
①;
②若,则关于x的一元二次方程没有实数解;
③点,在抛物线上上,若,,总有;
④若抛物线的顶点的轨迹上有两点,,则关于x的方程的两根之和大于1.
其中正确的是 (填写序号).
38.(24-25九年级上·北京西城·期末)如图,在平面直角坐标系中,已知点,其中,抛物线经过点和,以下四个结论:
①;②;③关于的一元二次方程无实根;④点,在抛物线上且在对称轴的同侧,当时,总有时,则.其中所有正确结论的序号是 .
39.(2025·湖北武汉·一模)开口向下的抛物线经过点,且.下列结论:①;②;③已知点在抛物线上,若,则;④若方程有两个不相等的实数根,则.其中正确结论的序号是 .
40.(24-25九年级上·湖北武汉·期中)已知抛物线(为常数,)经过点,,且,则下列四个结论:①;②;③若方程有两个不相等的实数根(且),则;④若,抛物线过点,且,则.其中正确的结论是 (填序号).
专题01 二次函数的图象与系数的关系(举一反三专项训练)
【人教版】
考卷信息:
本套训练卷共40题,选择题25题,填空题15题.题型针对性较高,覆盖面广,选题有深度,可加强学生对二次函数图象与各项系数符号之间的关系的理解!
一、单选题(25题)
1.(2025·安徽·中考真题)已知二次函数的图象如图所示,则( )
A. B. C. D.
【答案】C
【分析】根据二次函数图象的开口方向、对称轴位置、与轴交点及特殊点的函数值,结合二次函数性质,逐一分析选项 .本题主要考查了二次函数的图象与性质,熟练掌握二次函数中(开口方向)、(对称轴与共同决定)、(与轴交点)的意义及特殊点函数值的应用是解题的关键.
【详解】解: 二次函数图象中,开口向上,
.
对称轴,又,
,即.
抛物线与轴交点在负半轴,
.
选项A:,,,
两负一正相乘得正,
,该选项错误.
选项B:对称轴,由图象知对称轴,即,
又,两边乘得,,该选项错误.
选项C:当时,,即;当时,,
,该选项正确.
选项D:当时,,由图象知对应的函数值,
,该选项错误.
故选.
2.(2025·四川泸州·中考真题)已知抛物线的对称轴为直线,与轴的交点位于轴下方,且时,,下列结论正确的是( )
A. B. C. D.
【答案】D
【分析】本题主要考查了二次函数的图象与性质,二次函数与一元二次方程之间的关系,根据对称轴公式可得,即,据此可判断A;根据题意可得当时,,再由当时,,可得抛物线与轴的一个交点一定在直线和轴之间,则抛物线与轴的另一个交点一定在直线和直线之间,据此可判断B;当时,,再由,即可判断D;根据抛物线与轴的一个交点一定在直线和轴之间,当时,,根据题意不能确定的符号,则C选项不一定成立.
【详解】解:∵抛物线的对称轴为直线,
∴,
∴,故A选项中原结论错误,不符合题意;
∵抛物线与轴的交点位于轴下方,
∴当时,,
∵当时,,
∴抛物线与轴的一个交点一定在直线和轴之间,
∴抛物线与轴的另一个交点一定在直线和直线之间,
∴抛物线与轴有两个不同的交点,
∴关于的一元二次方程有两个不相同的实数根,
∴,故B选项中原结论错误,不符合题意;
∵当时,,且当时,,
∴抛物线开口向上,
∵抛物线与轴的另一个交点一定在直线和直线之间,
∴当时,,
∴,即,故D选项中原结论正确,符合题意;
当时,,
∵抛物线与轴的一个交点一定在直线和轴之间,
∴当时,的符号不确定,即的符号不确定,
∴不一定成立,故C选项不正确,不符合题意;
故选:D.
3.(2025·黑龙江绥化·中考真题)如图,二次函数与轴交于点、,与轴交于点,其中.则下列结论:
①;②方程没有实数根;③; ④.
其中错误的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】A
【分析】本题考查了二次函数图象的性质,掌握二次函数图象开口,对称轴直线,最值的计算方法是关键.
根据题意得到图象开口向上,对称轴直线为,,则,当时,代入计算可判定①;根据二次函数与直线的位置关系可判定②;根据题意得到,可判定③;根据函数最小值的大小可判定④;由此即可求解.
【详解】解:二次函数与轴交于点、,图象开口向上,
∴对称轴直线为,,
∴,
当时,,
∴,即,
∴,
∴,故①正确;
图象开口向上,对称轴直线为,
∴当时,函数有最小值,最小值轴的下方,
∴抛物线与直线两个不同的交点,
∴方程有两个不相等的实数根,故②错误;
∵二次函数与轴交于点,其中,
∴当,,
∴,
∵,
∴,
∴,
解得,,故③正确;
当时,函数有最小值,最小值为,,
∴,
∴,故④正确;
综上所述,正确的有①③④,错误的有②,
∴错误的有1个,
故选:A .
4.(2025·四川遂宁·中考真题)如图,已知抛物线(为常数,且)的对称轴是直线,且抛物线与轴的一个交点坐标是,与轴交点坐标是且.有下列结论:①;②;③;④关于的一元二次方程必有两个不相等实根;⑤若点在抛物线上,且,当时,则的取值范围为.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
【答案】C
【分析】本题考查了二次函数的图象与性质,一元二次方程根的判别式,熟练掌握以上知识点是解题的关键.根据函数图象结合二次函数的性质,先判断的符号即可判断①;进而根据对称性得出另一个交点坐标为,则当时,,即可判断②;根据,,结合抛物线的顶点坐标,即可判断③;求得的范围进而根据一元二次方程根的判别式判断一元二次方程的解情况即可判断④;根据,结合函数图象分析,即可得出,进而判断⑤,即可求解.
【详解】解:根据函数图象可得抛物线开口向下,则,对称轴为直线,则
∴ ,
又∵抛物线与轴交点坐标是,即,
∵,即,
∴,故①正确;
∵抛物线与轴的一个交点坐标是,对称轴为直线,
∴另一个交点坐标为,
∴当时,,故②错误;
∵,在抛物线的图象上,
∴,
又∵,
∴,
∴即,
∵,即,
∴,
∴即,
当时,取得最大值,最大值为,
∴,
∴,故③正确;
∵,,,
即,
∵
对称轴为直线,当时,的值随的增大而减小,
又∵,
∴,
∴当时,,
∴当时,恒成立,即必有两个不相等实根,故④正确;
∵若点在抛物线上,且,
∴,,
∵存在,
∴,,
即,,,
解得:,故⑤正确;
故正确的有①③④⑤,共4个.
故选:C.
5.(2025·四川宜宾·中考真题)如图,是坐标原点,已知二次函数的图象与轴交于两点,与轴交于点,顶点为,对称轴为直线,其中,且.以下结论:①;②;③是钝角三角形;④若方程的两根为、,则,.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】首先由抛物线开口向上得到,然后由对称轴得到,然后由抛物线与y轴交于负半轴得到,即可判断①;由对称轴为直线得到,然后将代入抛物线得到,代入得到,然后根据得到,即可判断②;设抛物线对称轴与x轴交于点E,将代入抛物线得到,求出,然后求出,得到,得到,即可判断③;分别将和代入方程,整理求出和或6,进而求解即可.
【详解】∵抛物线开口向上
∴
∵对称轴为直线
∴
∵抛物线与y轴交于负半轴
∴
∴,故①错误;
∵对称轴为直线
∴
∵在抛物线上
∴
∴
∴
∵
∴
∴,故②正确;
如图所示,设抛物线对称轴与x轴交于点E,
将代入
将,代入得,
∴
∵
∵对称轴为直线,
∴
∴
∴
∵
∴
∴
∴是钝角三角形,故③正确;
∵
∴当时,,
∴方程转化为
解得;
∴当时,,
∴方程转化为
解得或6;
∵方程的两根为、
∴,,故④正确.
综上所述,其中正确结论有3个.
故选:C.
【点睛】此题考查了二次函数的图象和性质,二次函数和x轴交点问题,解直角三角形,解一元二次方程等知识,解题的关键是掌握以上知识点.
6.(2025·山东烟台·中考真题)如图,二次函数的部分图象与轴的一个交点位于和之间,顶点的坐标为.下列结论:①;②对于任意实数,都有;③;④若该二次函数的图象与轴的另一个交点为,且是等边三角形,则.其中所有正确结论的序号是( )
A.①② B.①③ C.①④ D.①③④
【答案】D
【分析】由二次函数的图象的开口向下,与轴交于正半轴,对称轴在轴的右侧,,,,可得①符合题意;结合当时,最大,当时,,可得②不符合题意;由,,可得,可得③符合题意;由,记的横坐标分别为,可得,结合,可得,可得④符合题意.
【详解】解:∵二次函数的图象的开口向下,与轴交于正半轴,对称轴在轴的右侧,
∴,,,
∴,故①符合题意;
∵顶点的坐标为,
∴当时,最大,
当时,,
∴,
∴,故②不符合题意;
∵二次函数的部分图象与轴的一个交点位于和之间,对称轴为直线,
∴,,
∴,,
∴,故③符合题意;
如图,为等边三角形,
∴,,,,
∴,
记的横坐标分别为,
∴,
∴,
当,则,,
∴,
∴,
∵,
∴,
∴,
∴,
故④符合题意;
故选:D
【点睛】本题考查的是二次函数的图象与性质,等边三角形的性质,锐角三角函数的性质,熟练的利用等边三角形的性质结合二次函数的图象解题是关键.
7.(2025·黑龙江齐齐哈尔·中考真题)如图,二次函数的图象与轴交于两点,,且.下列结论:①;②;③;④若和是关于的一元二次方程 的两根,且,则,;⑤关于的不等式 的解集为.其中正确结论的个数是( )
A.2 B.3 C.4 D.5
【答案】B
【分析】本题考查了二次函数图象与性质,根据抛物线开口,对称轴,以及与轴的交点,确定的符号,即可判断①,根据二次函数的图象过,得出,进而判断对称轴,得出,进而判断②和③,根据函数图象判断④,将一般式写成交点式得出 ,化简不等式为,求得解集,即可求解.
【详解】解:∵抛物线开口向上,
∴,
∵对称轴在轴的右侧,
∴,
∴,
∵抛物线与轴交于负半轴,
∴,
∴,故①正确,
∵二次函数的图象过,
∴,
∵二次函数的图象与轴交于两点,,且.
∴对称轴,即,
∴,
∴,
∴,故②正确;
∵,
∴
,
∴,故③错误;
④如图,
关于的一元二次方程 的两个根,即函数与的交点的横坐标,
∵,
∴若和是关于的一元二次方程 的两根,且,则,;故④正确;
⑤∵二次函数的图象与轴交于两点,,
∴
,
∴,,
∴,,
∴可化为,
即,
∵,
∴,
解得:或,
∴关于的不等式 的解集为或不是故⑤错误
故正确的有①②④,共3个,
故选:B
8.(2025·四川广安·中考真题)如图,二次函数(a,b,c为常数,)的图象交x轴于A,B两点,点A的坐标是,点B的坐标是,有下列结论:①;②;③关于x的方程的解是,;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】本题考查了二次函数的图象与性质、抛物线与x轴的交点等知识,熟练掌握二次函数的图象与性质是解题的关键;
根据图象可得:抛物线的开口向下,交y轴于正半轴,即得,进而可判断,即可判断结论①;当时,,即,可判断结论②;根据二次函数与x轴的交点结合二次函数的对称性即可判断结论③④,可得答案.
【详解】解:根据图象可得:抛物线的开口向下,交y轴于正半轴,
∴,
又∵抛物线的对称轴在y轴右侧,
∴,
∴,
∴,故结论①正确;
由函数的图象可得:当时,,即,
即,故结论②错误;
∵二次函数的图象交x轴于A,B两点,点A,点B,
∴关于x的方程的解是,,,故结论③④正确;
综上,结论正确的有3个,
故选:C.
9.(2025·四川达州·中考真题)如图,抛物线与x轴交于点,点,下列结论:①;②;③;④.正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】本题考查了二次函数的图象和性质以及二次函数与一元二次方程的关系,熟练掌握二次函数的图象与性质是解题的关键;
根据抛物线开口向上,与y轴交于正半轴,可得,根据抛物线与x轴交于点,点,当时,即可逐一判断,进而求解.
【详解】解:∵抛物线开口向上,与y轴交于正半轴,
∴,
∵抛物线与x轴交于点,点,当时,
∴抛物线的对称轴是直线,,,
故结论③④正确;
∴,即,,
故结论②正确;
∴,
故结论①正确;
综上,说法正确的有4个;
故选:D.
10.(2025·四川凉山·中考真题)二次函数的部分图像如图所示,其对称轴为,且图像经过点,则下列结论错误的是( )
A.
B.
C.若且,则
D.若两点都在抛物线的图像上,则
【答案】D
【分析】本题考查二次函数的图像和性质,根据图像判断系数之间的关系,从图像获取信息,根据二次函数的对称性,增减性,逐一进行判断即可.
【详解】解:由图像可知,抛物线的开口向下,与轴交于正半轴,
∴,
∵对称轴为直线,
∴,
∴,,故选项A,B正确,不符合题意;
∵且,
∴,
∴和关于对称轴对称,
∴;故选项C正确;不符合题意;
∵抛物线的开口向下,
∴抛物线上的点离对称轴越远,函数值越小,
若两点都在抛物线的图像上,
∵,
∴;故选项D错误,符合题意;
故选D.
11.(2025·湖北十堰·模拟预测)抛物线(a为常数且),过点,且,下列结论:①;②;③;④若关于x的方程有实数根,则.其中正确的结论有( )
A.①③④ B.②③④ C.①②③ D.②④
【答案】D
【分析】本题考查了二次函数的图象与性质,二次函数与一元二次方程的关系.熟练掌握二次函数的图象与性质,二次函数与一元二次方程的关系是解题的关键.
根据及过点,且,结合二次函数的性质与判别式条件,逐一分析各结论的正确性.
【详解】解:①∵抛物线(a为常数且),过点,
∴抛物线可表示为,
∴,
∵
∴,
∴,
∴,结论①错误;
②将代入,得
∵,
∴,
∵,
∴,结论②正确;
③∵,
∴
∵
∴
∴
∵
∴,结论③错误;
④∵
∴
∴
∴
∴
∵,
∵,结论④正确.
综上,正确结论为②④,
故选:D.
12.(2025·黑龙江齐齐哈尔·模拟预测)如图,二次函数的图象与x轴交于点,与y轴交于点B,对称轴为直线,下列四个结论:①;②;③方程的两根和为1;④若,则,⑤点,在抛物线上,且当时,;其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】此题考查了二次函数的图象和性质,数形结合是解题的关键,利用开口方向和对称轴的位置即可判断①,利用对称轴和特殊点的函数值即可判断②由根与系数的关系可得出,由代入即可判断③,求出,进一步得到,又根据得到,即可判断④. ⑤当点和关于对称轴对称时,解得m,若点A和点B向左移动时结合对称轴左侧的递减性,以及即可得到m的取值范围.
【详解】解:①函数图象开口方向向上,
;
对称轴在轴右侧,
、异号,
,
∵抛物线与轴交点在轴负半轴,
,
,故①错误;
②二次函数的图象与轴交于点,与轴交于点,对称轴为直线,
时,,
,
,
,
,
∵,
,故②正确;
③设方程的两根为和,
∴,
,
∴,故③错误.
④,
∴根据抛物线与相应方程的根与系数的关系可得,
,
,
,
,
,
,
故④正确;
⑤点,在抛物线上,
当时,,解得,
∵,
∴,则⑤正确;
故选:C.
13.(2025·江苏无锡·模拟预测)已知抛物线(a,b,c是常数)开口向上,过两点,且.下列四个结论中正确的结论有( )
①;②若时,则;
③若点在拋物线上,,且,则;
④时,关于x的一元二次方程必有两个不相等的实数根.
A.①③ B.②③ C.②④ D.③④
【答案】C
【分析】本题考查了二次函数图象的性质,一元二次方程根与系数的关系,掌握二次函数图象的对称性,增减性,二次函数与轴的交点,一元二次方程根与系数的关系是解题的关键.
根据二次函数图象开口向上,即,对称轴直线为,且可判定①;根据二次函数对称轴直线的计算方法,图象过点的知识结合可判定②;根据题意可得点到对称轴的距离大于点到对称轴的距离,图象开口向下,由离对称轴越远值越小可判定③;根据二次函数图象的性质,一元二次方程根与系数的关系可判定④;由此即可求解.
【详解】解:抛物线(,,是常数)开口向上,
∴,
∵二次函数图象过两点,
∴对称轴直线为,
∵,
∴,
∴,故①错误;
若,则,
∴,
把代入抛物线解析式得,,
∴,
∴,故②正确;
∵对称轴直线为,且,
∴,
已知点,在抛物线上,,且,
∴,
∴点到对称轴的距离大于点到对称轴的距离,
∴,故③错误;
已知抛物线过两点,
∴设抛物线解析式为:,
令,整理得,,
∴,
∵,,
∴,
∴,
∴
∴,
∴关于的一元二次方程必有两个不相等的实数根,故④正确.
综上所述,正确的有②④,
故选:C.
14.(2025·青海·三模)如图是抛物线图象的一部分,其顶点坐标为,与x轴的一个交点为,直线与抛物线交于A,B两点,下列结论:①;②;③抛物线与x轴的另一个交点是;④不等式的解集为;⑤方程有两个相等的实数根;其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】由题意,,,可判断错误;观察对称轴即可判断正确;根据对称性求出抛物线与轴的另一个交点是可判断④错误;抛物线 图象与直线只有一个交点,方程有两个相等的实数根,故⑤正确.
【详解】∵抛物线开口向上,
∴,
∵抛物线交轴于负半轴,
∴,
∵对称轴在轴右边,
∴,
∴,
∴,故错误,
∵顶点坐标为,
∴,
∴,故②正确;
∵,对称轴为直线,
∴抛物线与轴的另一个交点是,故错误,
由题意:图象与直线交于,两点,
∴当时,即不等式的解集为,故④正确,
∵抛物线 图象与直线只有一个交点,
∴方程有两个相等的实数根,故⑤正确,
故选C.
【点睛】此题考查了二次函数的性质、二次函数与不等式,二次函数与一元二次方程等知识,解题的关键是灵活运用所学知识解决问题,学会利用数形结合的思想解决问题.
15.(2025·陕西西安·模拟预测)抛物线的对称轴为直线,与x轴的一个交点A在点和之间,其部分图象如图所示,以下结论正确的有( )
①;②;③若m为任意实数,则有;④点,在其图象上,若,且,则一定有.
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】本题考查了二次函数的图象和性质,根据二次函数对称轴和图象得出的符号,即可判断①;由时,,即可判断②;最值判断③;根据二次函数性质可判断④;掌握二次函数的图象和性质是解题的关键.
【详解】解:∵抛物线的对称轴为,
∴,
∴,
∵抛物线开口向下,
∴,
∴,
∵抛物线对称轴为,与轴的一个交点在点和之间,
∴抛物线与轴的另一个交点在点和之间,
∴抛物线与轴的交点在轴的正半轴上,
∴,
∴,故①正确;
∵抛物线与轴的另一个交点在点和之间,
∴时,,
即,
∵,
∴,故②正确;
∵抛物线的开口向下,对称轴为直线,
∴当时,函数值最大,
∴当m为任意实数时,则:,
∴,故③正确;
∵抛物线开口向下,图象上有两点和,对称轴为 ,,且,
∴点在对称轴右侧,
当时, 在抛物线的右侧,随的增大而减小,
∵,
∴,
当时,点到对称轴的距离为,点到对称轴的距离为,
∵,
∴,
又∵抛物线开口向下,抛物线上的点离对称轴的越近,函数值越大,
∴,
∴图象上有两点和,若,且,则一定有,
故④正确;
∴结论正确的有个,
故选:.
16.(2025·黑龙江齐齐哈尔·三模)如图所示是二次函数的部分图象,该函数图象的对称轴是直线,图象与轴交点的纵坐标是.则下列结论:①;②方程一定有两个不相等的实数根:③当时,;④;⑤抛物线上有两点,,若,则.其中正确结论的个数有( )
A.个 B.个 C.个 D.个
【答案】C
【分析】根据抛物线的对称轴可得,进而判断结论①,结合一元二次方程跟的判别式和抛物线的开口方向,可得,进而判断结论②,根据抛物线的增减性,函数值可判断结论③,根据抛物线的对称性得出抛物线与轴的另一个交点在和之间,结合函数值得出,进而判断结论④,根据抛物线的对称性得出点关于对称轴的对称点坐标为,结合抛物线的增减性即可得出时,,进而判断结论⑤,即可求解.
【详解】解:∵二次函数的对称轴为,
即,
∴,
∴,故①结论正确;
∵,
∴,
整理得,
则,
∵抛物线开口向下,
∴,
故,,
∴,
故方程一定有两个不相等的实数根,②结论正确;
∵,,
故抛物线的解析式为,
当时,,
当时,,
∵,
∴,
∵抛物线的对称轴是,故抛物线的最大值为;
当时,,
故当时,;即③结论正确;
根据图象可得:抛物线与轴的一个交点在和之间,抛物线的对称轴为,
故抛物线与轴的另一个交点在和之间,
当时,,
∵,,
∴,
∴,故④结论错误;
∵抛物线的对称轴为,
故点关于对称轴的对称点坐标为,
∵抛物线的开口向下,
故抛物线在对称轴的左侧,随的增大而增大,抛物线在对称轴的右侧,随的增大而减小,
若,
则,故⑤结论错误;
综上,结论正确的有①②③,有个.
故选:C.
【点睛】本题考查了二次函数的性质,抛物线与轴的交点问题,抛物线与轴的交点问题,二次函数图象与系数的关系,一元二次方程跟的判别式等.解题的关键是掌握二次函数的图象与性质.
17.(2025·湖北襄阳·模拟预测)已知抛物线(,,为常数,)经过点,开口向下,对称轴为直线.下列结论正确的是( )
A. B.
C. D.
【答案】D
【分析】本题考查了二次函数的图象与性质,二次函数的最值,二次函数的对称性,熟练掌握以上知识点是解题的关键.根据对称轴,可知,结合该抛物线过,可知,从而知道,判断出A;可知该抛物线与轴的另一个交点是,将其代入抛物线可判断C,根据抛物线与轴的交点个数,可判断B,从开口向下以及对称轴,可判断时,抛物线取得最大值,可判断D,从而得出答案.
【详解】解: 开口向下,
,
对称轴为直线,
,
,
过,对称轴为直线,
当时,,
,故C错误;
过,,
,
,
,
,
,故A错误;
过,,
,故B错误;
抛物线开口向下,对称轴为直线,
时,取最大值,
,
,故D正确;
故选:D.
18.(2025·贵州遵义·模拟预测)已知二次函数,其对称轴为.现有以下五个结论:①;②;③;④;⑤.其中正确的是________.
A.①②③④⑤ B.①③④⑤ C.②③④ D.①②⑤
【答案】B
【分析】根据抛物线的对称性,抛物线与x轴的交点,对称轴的两种表示方法,抛物线的增减性,最值等解答即可.
【详解】解:∵二次函数开口向上,
∴,
∵抛物线的图象与y轴的交点在负半轴上,
∴;
∵对称轴为直线,
∴,
∴,
∴,
故①正确;
∵,,
∴,,
∴,
故②错误;
∵抛物线的顶点在第四象限,
∴,
故③正确;
∵对称轴为直线,
∴,
∵,
∴,
∴,
故④正确;
∵对称轴为直线,
∴,
∴,
∴,
故⑤正确,
故选:B.
【点睛】本题考查了抛物线的对称性,抛物线的顶点坐标属性,根的判别式,抛物线与各项系数的符号关系,熟练掌握性质是解题的关键.
19.(2025·福建福州·三模)已知抛物线与轴交于点,其中.以下四个结论:①;②;③函数的最小值大于;④不等式的解集为.其中正确结论的序号为( )
A.①② B.①③ C.②③ D.①④
【答案】A
【分析】本题考查了二次函数的图象和性质,二次函数和一次函数的交点问题,利用数形结合的思想解决问题是关键.
根据题意画出函数大致图象,得到a、b同号,,可判断①结论;根据,得,可判断②结论;根据,二次函数最小值为,可判断③结论;根据函数与函数的交点为和,利用图象可判断④结论.
【详解】解:根据题意画出函数大致图象如下:
∵抛物线与轴交于点,其中,
∴抛物线开口向上,对称轴在之间,与y轴交点在负半轴,
∴a、b同号,,
∴,
∴①结论正确;
∵,
∴,
∴,
∴②结论正确;
,
∵,
∴,
∵,
∴当时,
,
∴③结论错误;
∵函数中,当时,,当时,,
∴函数与函数的交点为和,
∴不等式的解集为或,
∴④结论错误.
故选:A.
20.(2025·浙江绍兴·三模)如图,二次函数的图象经过点,,与y轴交于点C.下列结论:①;②;③;④当时,y随x的增大而增大.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】A
【分析】此题考查了二次函数的图象,二次函数图象与系数的关系,根据二次函数的图象判断式子的正负,正确理解二次函数的图象及性质是解题的关键.根据二次函数的图象及性质解答即可.
【详解】解:由图象可知,开口向下,与y轴交于正半轴,
∴,
∴,故①不正确;
∵二次函数的图象经过点,,
∴对称轴为直线,,
∴,,故②正确;
∴当时,图象有最高点,即函数最大值为,
∴当时,,
∴,故③不正确;
∵对称轴为直线,开口向下,
当时,y随x的增大而减小,
∴当时,y随x的增大而先增大后减小.故④不正确;
∴正确的为②,共1个,
故选:A.
21.(2025·贵州铜仁·三模)已知:二次函数的图象如图所示,下列结论中:①;②;③;④两根分别为,;⑤.其中正确的项有( )
A.2个 B.3个 C.4个 D.5个
【答案】B
【分析】本题主要考查了二次函数的图象与性质,牢记公式和数形结合是解题的关键.由抛物线开口向上知:,抛物线与轴的负半轴相交可知:,对称轴在轴的左侧可知:,即可判断①;根据对称轴为直线,得出,从而得出,即可判断②;由抛物线的性质可知,当时,有最小值,得出,即可判断③;根据抛物线的对称轴为, 且与轴的一个交点的横坐标为1, 得出另一个交点的横坐标为,即可判断④;根据当时,,得出,即可判断⑤.
【详解】解:①由抛物线开口向上知:,抛物线与轴的负半轴相交可知:,对称轴在轴的左侧可知:,
∴,故①正确;
②∵对称轴为直线,
∴,即,
∴,故②错误;
③由抛物线的性质可知,当时,有最小值,
∴,
即,故③正确;
④∵抛物线的对称轴为, 且与轴的一个交点的横坐标为1,
∴另一个交点的横坐标为,
∴方程的两根分别是1,,故④错误;
⑤由图像可得,当时,,即:,故⑤正确;
故正确选项有①③⑤共3个,
故选:B.
22.(2025·贵州黔西·二模)如图为二次函数的部分图象,已知抛物线的对称轴为直线,若点的坐标为,则以下结论错误的是( )
A.方程的两根为,
B.8
C.
D.若,是抛物线上的两点,且,则
【答案】B
【分析】此题考查二次函数的图象和性质以及二次函数与x轴交点,数形结合是解题的关键.
根据题意求出抛物线与x轴的另一个交点坐标为,即可判断A;首先由对称轴得到,然后将代入解析式得到,然后推出,根据,即可得到,进而判断B;然后由抛物线y轴交于正半轴得到,即可判断C;根据题意得到当时,y随x的增大而增大,即可判断D.
【详解】∵抛物线的对称轴为直线,若点的坐标为,
∴抛物线与x轴的另一个交点坐标为
∴方程的两根为,,故A正确;
∵抛物线的对称轴为直线,
∴
∴
将代入得,
∴将代入得,
∵抛物线开口向下
∴
∴,故B错误;
∵抛物线y轴交于正半轴
∴
∴,故C正确;
∵抛物线的对称轴为直线,开口向下
∴当时,y随x的增大而增大
∵若,是抛物线上的两点,且,
∴,故D正确.
故选:B.
23.(2025·湖北·模拟预测)如图,已知抛物线为常数,且的对称轴为直线,且该抛物线与轴交于点,与轴的交点在,之间(不含端点),有下列结论:①;②;③;④若方程的两根为,,则.其中正确的个数为( )
A.4 B.3 C.2 D.1
【答案】B
【分析】本题考查二次函数的图象与系数的关系,根与系数的关系,抛物线与x轴的交点,根据二次函数图象的开口方向、对称轴位置、与x轴的交点坐标、根与系数的关系等知识,逐个判断即可.
【详解】解:∵抛物线开口向上,
∴,
∵对称轴为直线,a、b同号,
∴,
∵抛物线与y轴的交点B在,之间,
∴,
∴,故①不正确;
∵对称轴为直线,且该抛物线与x轴交于点,
∴与x轴交于另一点,
∴当时,,故②正确;
由题意可得,方程的两个根为,
又∵,即,
∵,
∴,
因此,故③正确;
若方程的两根为,,即方程为:,则直线与抛物线的交点的横坐标为m,n,
∵直线过一、二、三象限,且过点,
∴直线与抛物线的交点在第一、第三象限,
由图象可知.故④正确;
综上所述,正确的结论有②③④,共3个,
故选:B.
24.(2025·江西新余·模拟预测)如图,已知二次函数的图象如图所示,其对称轴为直线,以下4个结论:①;②;③若点在该抛物线上,且,则;④.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】本题考查了二次函数的图像和性质,熟悉函数的图像和性质是解题关键.
利用二次函数的开口方向,对称轴的位置和与y轴的交点坐标即可求出①;令即可判断②;利用时函数值最大,即可判断③;令即可判断④.
【详解】①由图象可知:,
,故①正确;
②当时,,对称轴为直线,
∴当时,,
∴,故②正确;
③当时,y的值最大,此时,,
而当时,,
∴,
∴,
∴,即,
∵,
∴,
∴,故③正确;
④当时,,对称轴为直线
∴当时,,
∴,
∴,故④错误;
故选:C.
25.(2025·黑龙江齐齐哈尔·二模)如图所示是二次函数的部分图象,该函数图象的对称轴是直线,图象与轴交点的纵坐标是2.则下列结论:①;②方程一定有一个根在和之间;③方程一定有两个不相等的实数根;④点,在抛物线上,且,当时,;⑤函数的最大值大于.其中正确结论的个数为( )
A.5个 B.4个 C.3个 D.2个
【答案】B
【分析】本题考查抛物线与x轴的交点,根与系数的关系,二次函数的性质,二次函数图象上点的坐标特征,解题的关键是掌握二次函数的图象和性质,熟练运用数形结合的方法解决问题.根据二次函数的对称性,开口方向等来判断结论①②,根据二次函数与一元二次方程的关系来判断结论③,根据函数的增减性,函数值判断结论④⑤即可.
【详解】解:抛物线的对称轴为直线,
,
,即,故①正确;
抛物线的对称轴为直线,与x轴的一个交点的横坐标在2和3之间,
抛物线与x轴的另一个交点的横坐标在和0之间,
∴方程一定有一个根在和0之间,故②错误;
∵抛物线图象与轴交点的纵坐标是2,
,
,
,
令,得,
或,
,
,
∴方程一定有两个不相等的实数根,故③正确;
抛物线的开口向下,
抛物线上的点距离对称轴越远y值越小,距离对称轴越近y值越大,
,
,
,
,
,
点到对称轴的距离是,点到对称轴的距离是,
,故④正确;
如图,当时,,
,
,
,
当时,,
函数的最大值大于,故⑤正确,
综上所述,正确的结论有:①③④⑤,共4个,
故选:B.
二、填空题(15题)
26.(2025·四川绵阳·三模)已知二次函数的图象如图所示,根据已知信息有下列结论:①;②;③;④.其中正确的是 .
【答案】①②④
【分析】本题主要考查二次函数的图象及性质,做题时会用数形结合的思想进行思考,从而判断函数解析式中各系数关系的正负性是解题的关键.由二次函数的图象及性质,逐个结论进行判段,从而解答本题.
【详解】解:由抛物线的开口方向可知:,
由对称轴的位置,可知:,
不等式两边同时乘以得:,
可得:,,
结论①正确;②正确;
由,,可知:,
由抛物线与轴的交点可知:,
,
结论③错误;
由二次函数与一元二次方程的联系得,关于的方程有两个不相等的实数根,
,
,
由上可知,,,,
,,
,
结论④正确;
综上所述:①②④正确;
故答案为:①②④.
27.(2025·四川自贡·二模)如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下面五个结论正确的序号为 .
①; ②; ③;④;⑤时,
【答案】②③④⑤
【分析】此题主要考查图象与二次函数系数之间的关系,解题关键是注意掌握数形结合思想的应用.
根据对称轴位置及图象开口向上可判断出的符号,从而判断①;利用对称轴,可判断②;利用对称轴和开口向上,即可判断最小值,从而判断③的正误;由二次函数的性质即可判断④;由推出,,得到,即可得到,可判断⑤.
【详解】解:抛物线开口向上,
,
抛物线对称轴为直线,
,
,
,
抛物线与轴交于点在轴的负半轴,
,
,
故结论①错误;
二次函数的图象与轴交于点,对称轴为直线,抛物线与轴的另一个交点为,
,
故结论②正确;
,
,
,
,
,
故结论③正确;
对称轴为直线,
函数的最小值为,
,
,
故结论④正确;
,
,
,
,
,
,
,
,
故结论⑤正确;
综上所述,结论正确的是②③④⑤;
故答案为:②③④⑤.
28.(2025·山东烟台·一模)已知抛物线(a,b,c均为常数,且)经过点,下列结论:①;②;③当时y随x的增大而增大;④关于x的方程有两个不相等的实数根.其中正确结论的个数是 个.
【答案】4
【分析】本题考查的是二次函数图象与系数的关系、一元二次方程根的判别式、抛物线与轴的交点,熟记二次函数的对称轴、增减性以及一元二次方程根的判别式是解题的关键.根据抛物线经过点、结合题意判断①②;根据抛物线的对称性判断③;根据一元二次方程根的判别式判断④.
【详解】解:②∵抛物线经过点,
∴,
∵,
∴,即,故②正确;
①∵,,
∴,
∴,故①正确;
③∵
∴对称轴,
∴当时,随的增大而增大,故③正确;
④∵,
∴,
对于方程,,
∴方程有两个不相等的实数根,故④正确;
综上所述,其中正确结论的个数是4.
故答案为:4.
29.(2025·江苏淮安·二模)如图是二次函数图象的一部分,对称轴为,且经过点 .以下说法:①;②;③;④若是抛物线上的两点,则;⑤(其中),其中说法正确的是 .
【答案】①②③④⑤
【分析】本题考查了二次函数图象与系数的关系:二次项系数a决定抛物线的开口方向和大小.当时,抛物线向上开口;当时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时,对称轴在y轴左;当a与b异号时,对称轴在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于抛物线与x轴交点个数由判别式确定:时,抛物线与x轴有2个交点;时,抛物线与x轴有1个交点;时,抛物线与x轴没有交点.
利用抛物线开口方向得到,利用抛物线的对称轴方程得到,利用抛物线与y轴的交点在x轴上方得到,则可对①进行判断;利用抛物线经过点得到,则可对③进行判断;同时得到,加上,则可对②进行判断;通过比较点到直线的距离与点到直线的距离的大小可对④进行判断;利用时,函数值最大以及可对⑤进行判断.
【详解】解:抛物线开口向下,
,
抛物线的对称轴为直线,
,
抛物线与y轴的交点在x轴上方,
,
,所以①正确;
抛物线经过点,
,所以③正确;
,
,所以②正确;
点到直线的距离比点到直线的距离大,
;所以④正确;
抛物线的对称轴为直线
当时,函数值最大,
,
,
即,所以⑤正确.
故答案为:①②③④⑤.
30.(2025·江苏扬州·一模)如图,二次函数图像的对称轴是直线,下列结论:①;②;③(m为常数);④若关于x的方程恰有三个解,则,其中正确的是 (填序号).
【答案】①②③④
【分析】本题考查根据二次函数的图象判断式子符号,二次函数图象与各项系数符号.熟练掌握二次函数的图象和性质是解题关键.
根据二次函数的图象和性质逐项判断即可.
【详解】解:由二次函数图象可知,
∵该二次函数对称轴为,
∴,
∴,
∴,故①正确;
由图象可知,当时,,即.
∵,
∴,故②正确;
当时,y取得最小值,
∴,即,故③正确;
当时,,
∴顶点坐标为,
根据题意得,
即将位于x轴下方的图像向上翻折,
∴翻折后的顶点坐标为,
∵若关于x的方程恰有三个解,
∴即函数与恰有三个解,
即恰好经过向上翻折后的图像的顶点,
∴,
∵,
代入得到,则,
故④正确;
综上可知正确的结论为①②③④,
故答案为:①②③④.
31.(2025·湖北武汉·模拟预测)抛物线(是常数)经过点和两点,且.以下四个结论:①;②若,则;③若,则关于的一元二次方程必有两个相等的实数根;④点、在抛物线上,若,,总有,则.其中正确的是 (填写序号).
【答案】①②
【分析】本题考查二次函数与方程、不等式的关系,二次函数的图象与性质,根据抛物线经过点和两点得到对称轴为直线,,再据此逐个分析即可.
【详解】解:∵抛物线(是常数)经过点和两点,且,
∴对称轴为直线,
∴,
∴,
故①正确;
∵抛物线(是常数)经过点和两点,且,
∴方程的解集为或,
∴不等式的解集为或,
∴不等式解集为或,
解得或,
∴若,则;
故②正确;
∵抛物线经过点,
∴,
∵,
∴,
∴关于的一元二次方程的判别式,
∴关于的一元二次方程必有两个实数根,但是不一定是相等实数根,
故③错误;
∵抛物线对称轴为直线,,
∴在对称轴右边随的增大而增大,
∵若,总有,
∴总在对称轴右边,
∴,
∵,
∴,
解得,
∵,
∴,
故④错误;
综上所述,正确的有①②,
故答案为:①②.
32.(2025·四川南充·一模)如图,二次函数的图象与x轴交于点,与y轴的交点B在与之间(不包括这两点),对称轴为直线.下列结论:①;②若点,点是函数图象上两点,则;③当时,将抛物线先向上平移4个单位,再向右平移1个单位,得到抛物线;④;⑤.
其中正确的有 (填序号)
【答案】①④⑤
【分析】根据二次函数图象的开口方向,对称轴的位置,与y轴交点的位置判断①符合题意;根据点N坐标和二次函数的对称轴确定二次函数图象过点,再根据二次函数的增减性即可判断②不符合题意;使用待定系数法求出抛物线解析式,再根据二次函数图象平移规律即可判断③不符合题意;把点A坐标和点A关于对称轴对称的点的坐标代入二次函数解析式,然后用a表示c,再根据点C的位置和不等式的性质即可判断④符合题意;根据二次函数的最值得到不等式,再根据不等式的性质和等价代换思想即可判断⑤符合题意.
【详解】解:∵二次函数图象开口方向向下,对称轴在y轴右侧,与y轴的交点在y轴的正半轴,
∴,,.
∴.
∴.故①符合题意.
∵点是函数图象上一点,对称轴是直线,
∴二次函数图象经过点.
∵二次函数图象开口方向向下,
∴当时,y随x的增大而增大.
∵函数图象上一点,
∴.故②不符合题意.
∵,二次函数图象对称轴是直线,
∴设二次函数解析式为.
把点坐标代入二次函数解析式得.
解得.
∴二次函数解析式为.
∴抛物线先向上平移4个单位,再向右平移1个单位得到抛物线为.故③不符合题意.
∵二次函数图象过点,二次函数对称轴是直线,
∴二次函数图象过点.
把点和代入二次函数解析式中得
用a来表示b和c得
∵二次函数图象与y轴的交点B在与之间(不包括这两点),
∴.
∴.
∴.故④符合题意.
∵二次函数图象开口方向向下,对称轴为直线,
∴二次函数在时取得最大值.
∴当时,,即.
∴.
∵,
∴.
∴.
∴.故⑤符合题意.
故①④⑤符合题意.
故答案为:①④⑤.
【点睛】本题考查二次函数的图象与系数关系,二次函数的对称性,二次函数的增减性,二次函数图象平移规律,待定系数法求二次函数解析式,二次函数的最值,不等式的性质,综合应用这些知识点是解题关键.
33.(2025·湖北武汉·模拟预测)已知抛物线经过第四象限点,下列四个结论:①;②;③若抛物线经过点,则;④.其中正确的结论是 .(只填序号)
【答案】①②③④
【分析】本题主要考查了二次函数的图像和性质,不等式的性质,根据点所在象限可得出,由二次函数的图像和性质得出,即,结合已知条件可判断①,把变形成即可判断②, 把代入二次函数解析得出,结合即可判断③,利用不等式的性质即可得出判断④.
【详解】解:∵点在第四象限,
∴,
把代入,即,
∵,
∴
∴,故①正确,
∴,
∴,
由可得出,
∴,即恒成立,故②正确,
若抛物线经过点,
∴,
∵,
∴,
∴,则,故③正确,
∵,,
∴,
∴可变形为:,
即,
整理得:,
∵,
∴
∴,显然成立,故④成立,
故答案为:①②③④
34.(2025·吉林长春·一模)如图,二次函数的图象与x轴交于、两点,与y轴交于点C,顶点为D,则下列结论:①;②;③若是等腰三角形,的值有2个;④当是直角三角形时.其中正确的是 .(只需填写序号)
【答案】①②③
【分析】由图象可得对称轴为直线,可得,可判断①;将点A坐标代入解析式可得,可判断②;由等腰三角形的性质和两点距离公式,可求a的值,可判断③;由直角三角形的性质和两点距离可求或,可判断④,即可求解.
【详解】解:∵二次函数的图象与x轴交于、两点,
∴对称轴为直线,
∴,
∴,
故①正确,
当时,,
∴,
∴,
∴,
故②正确;
∵二次函数,
∴点,
∴,,
当时,,
∴(正数值已舍去),
当时,,
∴(正数值已舍去),
∴当是等腰三角形时,a的值有2个,
故③正确;
∵二次函数,
∴顶点,
∴,,,
若,可得,
∴,
∴,
若,可得,
∴,
∴,
∴当是直角三角形时,或,
故④错误.
故答案为:①②③.
【点睛】本题考查了抛物线与x轴的交点,二次函数图象与系数关系,等腰三角形的性质,直角三角形的性质等知识,灵活运用这些性质进行推理是本题的关键.
35.(2025·湖北武汉·模拟预测)抛物线是常数,经过两点,且.
下列五个结论:
①;
②;
③若抛物线经过点,则;
④若关于的不等式的解集为,则;
⑤点在抛物线上,若,总有,则.
其中正确的结论是 (填写序号).
【答案】①③⑤
【分析】根据抛物线的对称性,增减性,对称轴的两种表示方法,抛物线与不等式,解答即可.
【详解】解:∵抛物线是常数,经过两点,且.
∴,,,
∴,
∴;
故①正确;
∵抛物线是常数,经过两点,且.
∴是方程的两个不相等的实数根,
∴;
故②错误;
∵抛物线经过点,
∴,
∵,
解得,
∵,
∴,
∴;
∴;
解得,
故③正确;
∵关于的不等式的解集为,
∴,
∴的两个根为,,
∵关于的不等式的解集为,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
故④错误;
∵点在抛物线上,抛物线的对称轴为,,总有,
∴,且,
解得,
∵
∴.
故⑤ 正确,
故答案为:①③⑤.
【点睛】本题考查了抛物线的对称性,抛物线与不等式,对称轴的两种表示方法,抛物线的增减性,熟练掌握性质是解题的关键.
36.(24-25九年级上·广东珠海·期末)如图,抛物线与x轴交于A、B两点,与轴的正半轴交于点C,对称轴是直线,其顶点在第二象限,给出以下结论:①;②;③若,则;④不论m取任何实数,均有.其中正确的有 .
【答案】①②③
【分析】本题主要考查了二次函数与系数的关系、二次函数图像上点的坐标特征及抛物线与轴的交点,根据所给函数图像,得出,,的符号,再结合抛物线的对称性及增减性对所给结论依次进行判断即可.熟知二次函数的图像与性质是解题的关键.
【详解】解:由所给图像可知,
,,,
所以.
故①正确.
因为抛物线的对称轴为直线,
所以,
则.
故②正确.
因为点坐标为,
由得,,
所以点的坐标为,
则,
所以.
因为抛物线的对称轴为直线,且点坐标为,
所以点的坐标为.
由得,
,
所以.
故③正确.
因为抛物线的对称轴为直线,且开口向下,
所以当时,二次函数有最大值,
即对于抛物线上的任意一点(横坐标为,总有,即.
故④错误.
故答案为:①②③.
37.(2025·湖北武汉·模拟预测)抛物线(a,b,c是常数,)经过,两点,且,下列四个结论:
①;
②若,则关于x的一元二次方程没有实数解;
③点,在抛物线上上,若,,总有;
④若抛物线的顶点的轨迹上有两点,,则关于x的方程的两根之和大于1.
其中正确的是 (填写序号).
【答案】①②④
【分析】根据抛物线(a,b,c是常数,)经过,两点,得出抛物线的对称轴为直线:,根据,得出即可判断①根据抛物线(a,b,c是常数,)经过,得出,根据,,得出,求出,得出,说明关于x的一元二次方程没有实数解,可判断②,根据抛物线的对称轴为:直线,设抛物线的对称轴为直线,得出,根据点,在抛物线上上,,,,分三种情况:当点,都在对称轴右侧时,当点,在对称轴两侧时,点在对称轴的左侧,即可判断③;先求出抛物线的顶点坐标在函数的图象上,根据,得出,根据抛物线的开口向下,对称轴为直线,得出在对称轴的右侧y随x的增大而减小,根据根与系数的关系即可判断④.
【详解】解:∵抛物线(a,b,c是常数,)经过,两点,且,
∴抛物线的对称轴为直线:,
,
∴,即,
∵,
∴,故①正确;
∵抛物线(a,b,c是常数,)经过,
∴,
∵,,
∴,
∴,
∵,
∴,
当时,一元二次方程为,
整理得:,
∵,
∴关于x的一元二次方程没有实数解,故②正确;
抛物线的对称轴为:
直线,
∵,
∴,
设抛物线的对称轴为直线,
∴,
∵点,在抛物线上上,,,,
∴当点,都在对称轴右侧时,,
当点,在对称轴两侧时,点关于对称轴的对称点为,
∵,
∴,
∴,
∵,,
∴点不可能都在对称轴的左侧,
综上分析可知:点,在抛物线上上,,时,,故③错误;
∵抛物线(a,b,c是常数,)经过,两点,
∴顶点坐标的横坐标为,,
顶点坐标的纵坐标为,
∴,
∵,
∴,
∴顶点坐标的横坐标,
把代入顶点坐标的纵坐标,
∵顶点坐标的横坐标为,
∴,
把代入得:,
∴抛物线的顶点坐标在函数的图象上,
∵,
∴,
∴抛物线的开口向下,对称轴为直线,
∴在对称轴的右侧y随x的增大而减小,
∵抛物线的顶点的轨迹上有两点,,
∴,,,
∴,
∴关于x的方程的两根之和,故④正确.
综上所述,①②④正确.
故答案为:①②④.
【点睛】本题主要考查二次函数图象与系数的关系,解题关键是掌握二次函数的性质,掌握二次函数与方程及不等式的关系.
38.(24-25九年级上·北京西城·期末)如图,在平面直角坐标系中,已知点,其中,抛物线经过点和,以下四个结论:
①;②;③关于的一元二次方程无实根;④点,在抛物线上且在对称轴的同侧,当时,总有时,则.其中所有正确结论的序号是 .
【答案】②④
【分析】本题主要考查了二次函数的图象与性质,抛物线上点的坐标的特征,对称轴,数形结合法,抛物线与轴的交点,二次函数与一元二次方程的联系,一元二次方程的根的判别式,熟练掌握二次函数的性质和二次函数与一元二次方程的联系是解题的关键.
①根据题中二次函数的图像判断开口方向,,以及抛物线与轴的交点,可判断的符号,进而可判断;
②由二次函数的图象知:当时,,;当时,,两式相加,化简可得
③一元二次方程的判别式 ,结合的关系与符号,进而可判断;
④设,且在对称轴右侧(在左侧同理),则,
,结合的关系与符号,进而可判断.
【详解】通过读图:
①因为,所以抛物线开口向上,
对称轴,由于,即对称轴,
可得,
抛物线与轴交于负半轴,所以,
综上,,结论①错误;
②: 二次函数的图象与轴交于由图可知,
又 ,
,
由二次函数的图象可知:
当时, ,
当时,,
两式相加,化简可得,结论②正确;
③一元二次方程的判别式 ,
因为,所以,
由,可得,所以 ,方程有两个不相等的实根,
结论③错误;
④设,且在对称轴右侧(在左侧同理),
则,
,
,
,
,
,
,
(在对称轴右侧),
,
又 ,
,
即 ,结论④正确.
综上,正确结论的序号是:②④.
39.(2025·湖北武汉·一模)开口向下的抛物线经过点,且.下列结论:①;②;③已知点在抛物线上,若,则;④若方程有两个不相等的实数根,则.其中正确结论的序号是 .
【答案】②④/④②
【分析】本题考查了二次函数的图象和性质,由题意可得抛物线的对称轴为直线,进而由得,得到,即可判断①;由抛物线经过点,得,得,即得,又由对称轴得,可得,即可得,即可判断②;利用二次函数的性质可判断③;由方程有两个不相等的实数根,可得抛物线与轴有两个不同的交点,根据根的判别式可判断④;综上即可求解,掌握二次函数的图象和性质是解题的关键.
【详解】解:∵抛物线经过点,
∴抛物线的对称轴为直线,
∵,
∴,即,
∴,
∵抛物线开口向下,
∴,
∴,故①错误;
∵抛物线经过点,
∴ ,
∴,
∴,
∵,
∴,
即,
∴,
∴,
∴,故②正确;
∵对称轴,抛物线开口向下,
∴当时,随的增大而增大,
∵,
∴,故③错误;
∵方程有两个不相等的实数根,
∴抛物线与轴有两个不同的交点,
即抛物线与轴有两个不同的交点,
∴,
∴,故④正确;
综上,正确结论的是②④,
故答案为:②④.
40.(24-25九年级上·湖北武汉·期中)已知抛物线(为常数,)经过点,,且,则下列四个结论:①;②;③若方程有两个不相等的实数根(且),则;④若,抛物线过点,且,则.其中正确的结论是 (填序号).
【答案】①②④
【分析】本题考查二次函数符号判断,根据得到抛物线过,再结合已知条件画出大致的函数图象,然后根据函数图象分析计算即可.
【详解】解:∵,
∴过,
∵,过点,,
∴函数的大致图象如下两种情况:
由函数图象可得,故①正确;
由函数图象可得当时,,
∵,
∴,
∴,
故②正确;
方程有两个不相等的实数根(且),可以看成抛物线与交点横坐标为,
有函数图象可得:当时,;当时,;
故③错误;
∵抛物线过点,
∴,
∴,整理得,,
∴,
∵抛物线过点,,
∴抛物线对称轴为直线,
∵,
∴,即,
∵,
∴解得,
∴,
故④正确;
综上所述,正确的有①②④,
故答案为:①②④.
同课章节目录
