江苏省江阴市峭岐中学苏教版高中数学必修二课件:1.2.2 两直线垂直 (共18张PPT)
文档属性
| 名称 | 江苏省江阴市峭岐中学苏教版高中数学必修二课件:1.2.2 两直线垂直 (共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 110.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-19 00:00:00 | ||
图片预览





文档简介
课件18张PPT。两直线的位置关系--两直线垂直复习提问:当直线的斜率不存在时,
直线 ∥ 的等价条件是 ⊥ 轴,
⊥ 轴且 与 不重合。 l1:A1x + B1y +C1 = 0,l2:A2x + B2y +C2 = 0(A1与B1不全为零、A2与B2也不全为零)
l1∥l2 ? A1 B2 – A2 B1= 0且A1 C2 – A2 C1 0
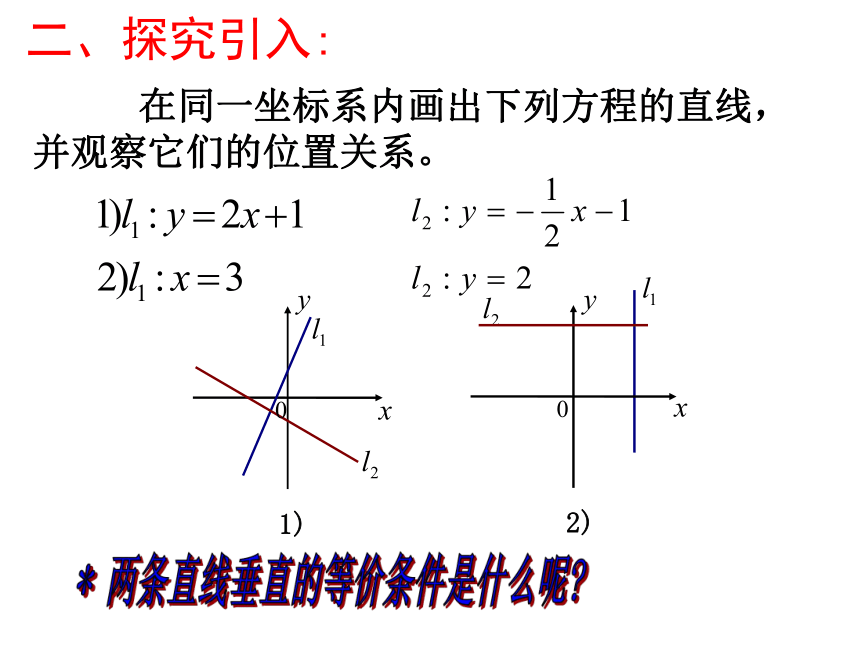
或A1 B2 – A2 B1= 0且B1 C2 – B2 C1 0当直线方程为一般式时:二、探究引入: 在同一坐标系内画出下列方程的直线,
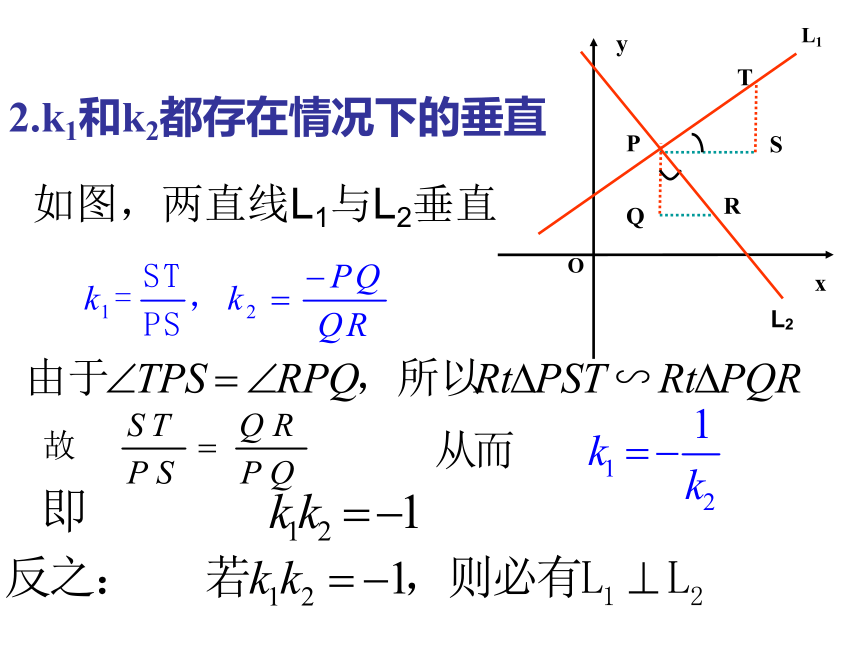
并观察它们的位置关系。2)* 两条直线垂直的等价条件是什么呢?三、讲授新知:1.特殊情况下的垂直如图,两直线L1与L2垂直P2.k1和k2都存在情况下的垂直归纳:一、特殊情况下的垂直二、斜率都存在情况下的垂直 如果它们互相垂直,则它们的斜率互为负倒数;反之如果它们的斜率互为负倒数则它们互相垂直。直线方程为一般式时例1:求过点A(2,1),且与直线 垂直的直线 的方程。分析: 解此题的关键在于抓住垂直这个概念,两直线垂直,说明这两条直线的斜率互为负倒数。其中一条直线方程知道,从而就可轻易的得出这条已知直线的斜率,那么,所求直线的斜率也就可以得出来了。法1:两直线垂直斜率互为负倒数其中一条直线的斜率知道求出另一条直线的斜率由点斜式求出所求直线的方程法2:待定系数法两直线斜率存在吗?斜率存在时,怎样确定两直线垂直?由两直线垂直,能得到什么结论?它与a有关系吗?例3、已知三角形的顶点A(2,4),B(1,-2),C(-2,3), 求BC边上的高AD所在的直线方程.分析:
确定直线方程需要几个条件?已知什么?还缺什么?怎么解决?一、判断下列两直线是否垂直,并说明理由.
(1)
(2)
(3)
练习2:基础练习:
1、当m为_____时,直线mx-(3m-2)y=7与2x+my=1互相垂直。
2、已知直线l1 :ax+by+2a=0与直线l2:(a-1)x+y+b=0互相垂直,且直线l1过点(-1,1),则a= ,
b= .0或4/32-23. 求过点A(3,2)且垂直于直线4x+5y-8=0的直线方程. 4.和直线x+3y+1=0垂直,且在x轴上的截距为2的直线方程。四、课堂小结:1、若两条直线斜率都存在,直线L1与L2的斜率分别为 k1,k2则:
L1⊥L2 ? k1 =-1/k2 L1⊥L2 ? k1k2=-1
2、两直线若一条直线无斜率另一条直线斜率为0,则这二直线互相垂直。
3、直线方程为一般式时五、作业布置:
直线 ∥ 的等价条件是 ⊥ 轴,
⊥ 轴且 与 不重合。 l1:A1x + B1y +C1 = 0,l2:A2x + B2y +C2 = 0(A1与B1不全为零、A2与B2也不全为零)
l1∥l2 ? A1 B2 – A2 B1= 0且A1 C2 – A2 C1 0
或A1 B2 – A2 B1= 0且B1 C2 – B2 C1 0当直线方程为一般式时:二、探究引入: 在同一坐标系内画出下列方程的直线,
并观察它们的位置关系。2)* 两条直线垂直的等价条件是什么呢?三、讲授新知:1.特殊情况下的垂直如图,两直线L1与L2垂直P2.k1和k2都存在情况下的垂直归纳:一、特殊情况下的垂直二、斜率都存在情况下的垂直 如果它们互相垂直,则它们的斜率互为负倒数;反之如果它们的斜率互为负倒数则它们互相垂直。直线方程为一般式时例1:求过点A(2,1),且与直线 垂直的直线 的方程。分析: 解此题的关键在于抓住垂直这个概念,两直线垂直,说明这两条直线的斜率互为负倒数。其中一条直线方程知道,从而就可轻易的得出这条已知直线的斜率,那么,所求直线的斜率也就可以得出来了。法1:两直线垂直斜率互为负倒数其中一条直线的斜率知道求出另一条直线的斜率由点斜式求出所求直线的方程法2:待定系数法两直线斜率存在吗?斜率存在时,怎样确定两直线垂直?由两直线垂直,能得到什么结论?它与a有关系吗?例3、已知三角形的顶点A(2,4),B(1,-2),C(-2,3), 求BC边上的高AD所在的直线方程.分析:
确定直线方程需要几个条件?已知什么?还缺什么?怎么解决?一、判断下列两直线是否垂直,并说明理由.
(1)
(2)
(3)
练习2:基础练习:
1、当m为_____时,直线mx-(3m-2)y=7与2x+my=1互相垂直。
2、已知直线l1 :ax+by+2a=0与直线l2:(a-1)x+y+b=0互相垂直,且直线l1过点(-1,1),则a= ,
b= .0或4/32-23. 求过点A(3,2)且垂直于直线4x+5y-8=0的直线方程. 4.和直线x+3y+1=0垂直,且在x轴上的截距为2的直线方程。四、课堂小结:1、若两条直线斜率都存在,直线L1与L2的斜率分别为 k1,k2则:
L1⊥L2 ? k1 =-1/k2 L1⊥L2 ? k1k2=-1
2、两直线若一条直线无斜率另一条直线斜率为0,则这二直线互相垂直。
3、直线方程为一般式时五、作业布置:
