2025 北京市北京中学初二 (下)期中数学(无答案)
文档属性
| 名称 | 2025 北京市北京中学初二 (下)期中数学(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 188.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-30 19:12:05 | ||
图片预览

文档简介
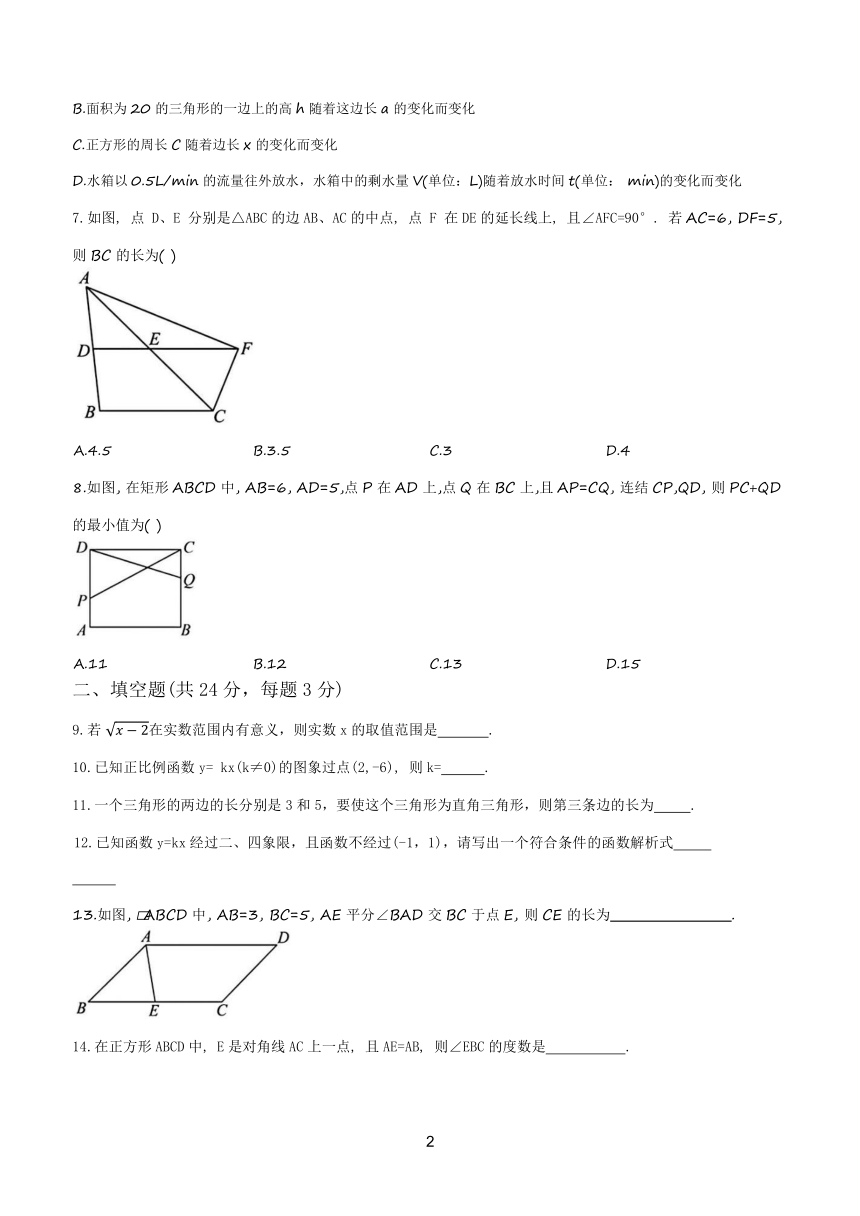
2025 北京北京中学初二 (下)期中
数学
满分100分 考试时间90分钟
考生须知
1.本试卷共 6页,满分100分,考试时间90分钟.
2.在试卷和答题卡上准确填写学校、班级、姓名、座位号.
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.
4.在答题卡上,选择题用2B铅笔作答,其他试题用黑色字迹签字笔作答.
5.考试结束,请将本试卷和答题卡一并交回.
一、选择题(共24分,每题3分)
下面1-8题均有四个选项,符合题意的选项只有一个.
1.下列各式是最简二次根式的是 ()
A.
2.若P(2,y )、Q(3,y )是正比例函数y= kx (k为常数, 且k<0) 图象上的两点, 那么y 与y 的大小关系是()
D.无法确定
3.下列计算正确的是()
4.下列曲线中,表示y是x的函数的是 ()
5.下列判断错误的是 ()
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一个角是直角的菱形是正方形
C.有一组邻边相等的平行四边形是菱形
D.对角线互相平分且相等的四边形是矩形
6.下列变量之间的关系,一个变量是另一个变量的正比例函数的是()
A.正方形的面积S随边长x的变化而变化
B.面积为20的三角形的一边上的高h随着这边长a的变化而变化
C.正方形的周长C随着边长x的变化而变化
D.水箱以0.5L/min的流量往外放水,水箱中的剩水量V(单位:L)随着放水时间t(单位: min)的变化而变化
7.如图, 点 D、E 分别是△ABC的边AB、AC的中点, 点 F 在DE的延长线上, 且∠AFC=90°. 若AC=6, DF=5, 则BC的长为( )
A.4.5 B.3.5 C.3 D.4
8.如图, 在矩形ABCD中, AB=6, AD=5,点P在AD上,点Q在BC上,且AP=CQ, 连结CP,QD, 则PC+QD的最小值为( )
A.11 B.12 C.13 D.15
二、填空题(共24分,每题3分)
9.若 在实数范围内有意义,则实数x的取值范围是 .
10.已知正比例函数y= kx(k≠0)的图象过点(2,-6), 则k= .
11.一个三角形的两边的长分别是3和5,要使这个三角形为直角三角形,则第三条边的长为 .
12.已知函数y=kx经过二、四象限,且函数不经过(-1,1),请写出一个符合条件的函数解析式
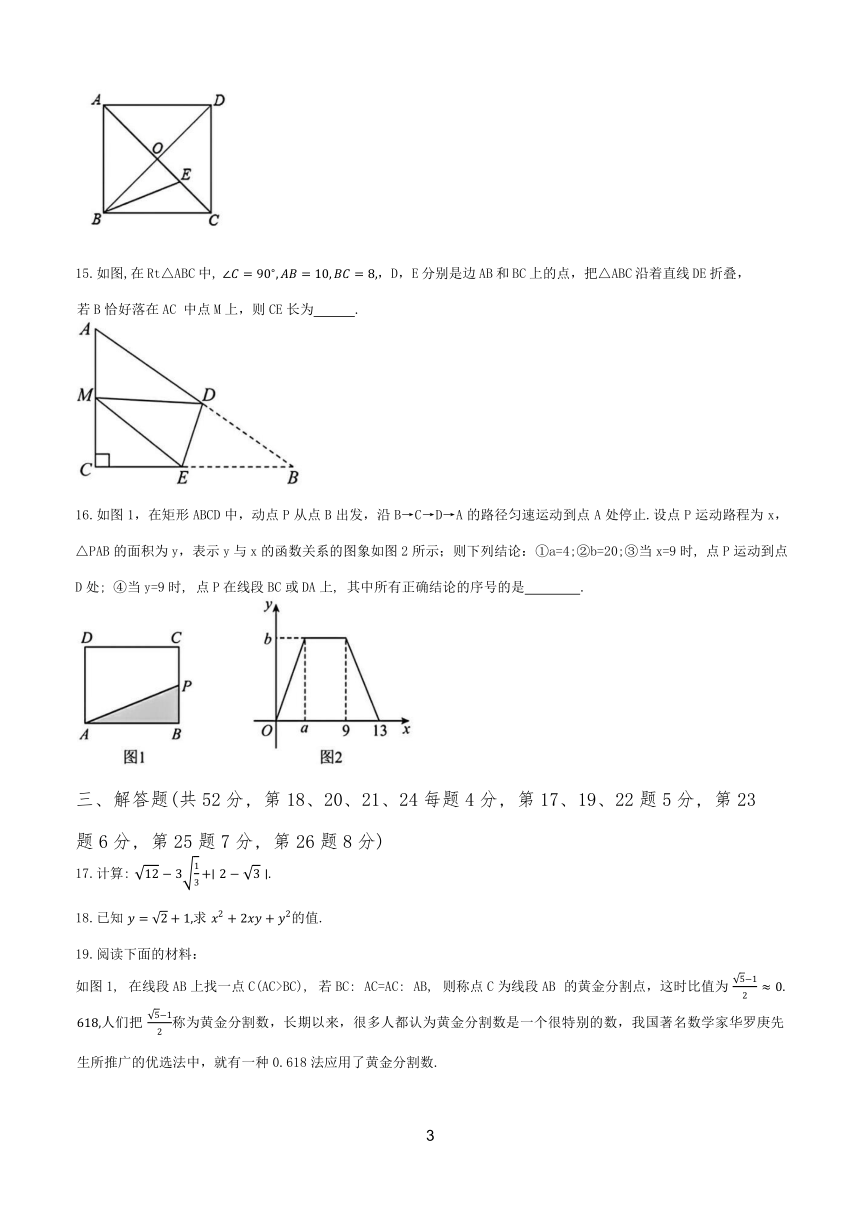
13.如图, ABCD中, AB=3, BC=5, AE平分∠BAD交BC于点E, 则CE的长为 .
14.在正方形ABCD中, E是对角线AC上一点, 且AE=AB, 则∠EBC的度数是 .
15.如图,在Rt△ABC中, ,D,E分别是边AB和BC上的点,把△ABC沿着直线DE折叠,若B恰好落在AC 中点M上,则CE长为 .
16.如图1,在矩形ABCD中,动点P从点B出发,沿B→C→D→A的路径匀速运动到点A处停止.设点P运动路程为x,△PAB的面积为y,表示y与x的函数关系的图象如图2所示;则下列结论:①a=4;②b=20;③当x=9时, 点P运动到点D处; ④当y=9时, 点P在线段BC或DA上, 其中所有正确结论的序号的是 .
三、解答题(共52分, 第18、20、21、24每题4分, 第17、19、22题5分, 第23题6分, 第25题7分, 第26题8分)
17.计算:
18.已知 求 的值.
19.阅读下面的材料:
如图1, 在线段AB上找一点C(AC>BC), 若BC: AC=AC: AB, 则称点C为线段AB 的黄金分割点,这时比值为 人们把 称为黄金分割数,长期以来,很多人都认为黄金分割数是一个很特别的数,我国著名数学家华罗庚先生所推广的优选法中,就有一种0.618法应用了黄金分割数.
我们可以这样作图找到已知线段的黄金分割点:如图2,在数轴上点O表示数0,点E表示数2,过点E作EF⊥OE, 且 连接OF;以F为圆心,EF 长为半径作弧,交OF 于H;再以O为圆心,OH 长为半径作弧,交OE 于点 P,则点 P就是线段OE 的黄金分割点.
根据材料回答下列问题:
(1)根据作图,写出图中相等的线段: ;
(2)求点P在数轴上表示的数,并写出 的值.
20.已知: ∠AOB.
求作:∠AOB的平分线.
作法:①以点O为圆心,适当长为半径画弧,交OA于点 C,交OB于点 D;
②分别以点C,D为圆心,OC长为半径画弧,两弧在∠AOB的内部相交于点P;
③画射线OP.
射线OP即为所求.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明: 连接PC, PD.
由作法可知OC=OD=PC=PD.
∴四边形OCPD是 .
∴OP平分∠AOB ( )(填推理的依据).
21.如图,在平行四边形ABCD中,E、F 分别是AB、CD边上的点且 求证:四边形AECF 为平行四边形.
22.如图,在 ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1) 求证: AB=CF;
(2) 连接DE, 若AD=2AB, 求证: DE⊥AF.
23.如图, 在△ABC中, AB=AC, D, E分别是AB, BC的中点,
(1) 求证: 四边形BDEF 是菱形;
(2) 连接DF交BC于点M, 连接CD, 若 求DM, CD的长.
24.水龙头关闭不严会造成滴水.下表记录了30min内7个时间点的漏水量,其中t表示时间,y表示漏水量.
时间t/ min 0 5 10 15 20 25 30
漏水量y/mL 0 15 30 45 60 75 90
解决下列问题:
(1)在平面直角坐标系中,描出上表中以各对对应值为坐标的点,根据描出的点连线;
(2)结合表中数据写出滴水量y关于时间t的函数解析式 (不要求写自变量的取值范围);
(3)在这种漏水状态下,若不及时关闭水龙头,估算一天的漏水量约为 mL.
25.在数学课上,老师说统计学中常用的平均数不是只有算术平均数一种,好学的小聪通过网络搜索,又得到了两种平均数的定义,他把三种平均数的定义整理如下:
对于两个数a,b,
称为a,b这两个数的算术平均数,
称为a,b这两个数的几何平均数,
称为a,b这两个数的平方平均数.
小聪根据上述定义,探究了一些问题,下面是他的探究过程,请你补充完整:
(1) 若a=-1, b=-2, 则M= , N= , P= ;
(2)小聪发现当a,b两数异号时,在实数范围内N没有意义,所以决定只研究当a,b都是正数时这三种平均数的大小关系.结合乘法公式和勾股定理的学习经验,他选择构造几何图形,用面积法解决问题:如图,画出边长为a+b的正方形和它的两条对角线,则图1中阴影部分的面积可以表示 N .
①请分别在图2,图3中用阴影标出一个面积为M ,P 的图形;
②借助图形可知当a,b都是正数时,M,N,P的大小关系是: (把M,N,P从小到大排列,并用“<”或“≤”号连接).
26.在平面直角坐标系xOy中,若P,Q为某个矩形不相邻的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.图1为点P,Q的“相关矩形”的示意图.
已知点A的坐标为(1,2)
(1) 如图2, 点B的坐标为(b,0).
①若b=-2, 则点A, B的“相关矩形”的面积是 ;
②若点A,B的“相关矩形”的面积是8,则b的值为 .
(2) 如图3, 点C在过点( 且平行x轴的直线l上,若点A,C的“相关矩形”是正方形,直接写出点C 的坐标;
(3)如图4,等边△DEF的边DE在x轴上,顶点F 在y轴的正半轴上,点D的坐标为(1,0),点M 的坐标为(m,2),若在△DEF的边上存在一点N,使得点M,N的“相关矩形”为正方形,请直接写出m的取值范围.
数学
满分100分 考试时间90分钟
考生须知
1.本试卷共 6页,满分100分,考试时间90分钟.
2.在试卷和答题卡上准确填写学校、班级、姓名、座位号.
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.
4.在答题卡上,选择题用2B铅笔作答,其他试题用黑色字迹签字笔作答.
5.考试结束,请将本试卷和答题卡一并交回.
一、选择题(共24分,每题3分)
下面1-8题均有四个选项,符合题意的选项只有一个.
1.下列各式是最简二次根式的是 ()
A.
2.若P(2,y )、Q(3,y )是正比例函数y= kx (k为常数, 且k<0) 图象上的两点, 那么y 与y 的大小关系是()
D.无法确定
3.下列计算正确的是()
4.下列曲线中,表示y是x的函数的是 ()
5.下列判断错误的是 ()
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一个角是直角的菱形是正方形
C.有一组邻边相等的平行四边形是菱形
D.对角线互相平分且相等的四边形是矩形
6.下列变量之间的关系,一个变量是另一个变量的正比例函数的是()
A.正方形的面积S随边长x的变化而变化
B.面积为20的三角形的一边上的高h随着这边长a的变化而变化
C.正方形的周长C随着边长x的变化而变化
D.水箱以0.5L/min的流量往外放水,水箱中的剩水量V(单位:L)随着放水时间t(单位: min)的变化而变化
7.如图, 点 D、E 分别是△ABC的边AB、AC的中点, 点 F 在DE的延长线上, 且∠AFC=90°. 若AC=6, DF=5, 则BC的长为( )
A.4.5 B.3.5 C.3 D.4
8.如图, 在矩形ABCD中, AB=6, AD=5,点P在AD上,点Q在BC上,且AP=CQ, 连结CP,QD, 则PC+QD的最小值为( )
A.11 B.12 C.13 D.15
二、填空题(共24分,每题3分)
9.若 在实数范围内有意义,则实数x的取值范围是 .
10.已知正比例函数y= kx(k≠0)的图象过点(2,-6), 则k= .
11.一个三角形的两边的长分别是3和5,要使这个三角形为直角三角形,则第三条边的长为 .
12.已知函数y=kx经过二、四象限,且函数不经过(-1,1),请写出一个符合条件的函数解析式
13.如图, ABCD中, AB=3, BC=5, AE平分∠BAD交BC于点E, 则CE的长为 .
14.在正方形ABCD中, E是对角线AC上一点, 且AE=AB, 则∠EBC的度数是 .
15.如图,在Rt△ABC中, ,D,E分别是边AB和BC上的点,把△ABC沿着直线DE折叠,若B恰好落在AC 中点M上,则CE长为 .
16.如图1,在矩形ABCD中,动点P从点B出发,沿B→C→D→A的路径匀速运动到点A处停止.设点P运动路程为x,△PAB的面积为y,表示y与x的函数关系的图象如图2所示;则下列结论:①a=4;②b=20;③当x=9时, 点P运动到点D处; ④当y=9时, 点P在线段BC或DA上, 其中所有正确结论的序号的是 .
三、解答题(共52分, 第18、20、21、24每题4分, 第17、19、22题5分, 第23题6分, 第25题7分, 第26题8分)
17.计算:
18.已知 求 的值.
19.阅读下面的材料:
如图1, 在线段AB上找一点C(AC>BC), 若BC: AC=AC: AB, 则称点C为线段AB 的黄金分割点,这时比值为 人们把 称为黄金分割数,长期以来,很多人都认为黄金分割数是一个很特别的数,我国著名数学家华罗庚先生所推广的优选法中,就有一种0.618法应用了黄金分割数.
我们可以这样作图找到已知线段的黄金分割点:如图2,在数轴上点O表示数0,点E表示数2,过点E作EF⊥OE, 且 连接OF;以F为圆心,EF 长为半径作弧,交OF 于H;再以O为圆心,OH 长为半径作弧,交OE 于点 P,则点 P就是线段OE 的黄金分割点.
根据材料回答下列问题:
(1)根据作图,写出图中相等的线段: ;
(2)求点P在数轴上表示的数,并写出 的值.
20.已知: ∠AOB.
求作:∠AOB的平分线.
作法:①以点O为圆心,适当长为半径画弧,交OA于点 C,交OB于点 D;
②分别以点C,D为圆心,OC长为半径画弧,两弧在∠AOB的内部相交于点P;
③画射线OP.
射线OP即为所求.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明: 连接PC, PD.
由作法可知OC=OD=PC=PD.
∴四边形OCPD是 .
∴OP平分∠AOB ( )(填推理的依据).
21.如图,在平行四边形ABCD中,E、F 分别是AB、CD边上的点且 求证:四边形AECF 为平行四边形.
22.如图,在 ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1) 求证: AB=CF;
(2) 连接DE, 若AD=2AB, 求证: DE⊥AF.
23.如图, 在△ABC中, AB=AC, D, E分别是AB, BC的中点,
(1) 求证: 四边形BDEF 是菱形;
(2) 连接DF交BC于点M, 连接CD, 若 求DM, CD的长.
24.水龙头关闭不严会造成滴水.下表记录了30min内7个时间点的漏水量,其中t表示时间,y表示漏水量.
时间t/ min 0 5 10 15 20 25 30
漏水量y/mL 0 15 30 45 60 75 90
解决下列问题:
(1)在平面直角坐标系中,描出上表中以各对对应值为坐标的点,根据描出的点连线;
(2)结合表中数据写出滴水量y关于时间t的函数解析式 (不要求写自变量的取值范围);
(3)在这种漏水状态下,若不及时关闭水龙头,估算一天的漏水量约为 mL.
25.在数学课上,老师说统计学中常用的平均数不是只有算术平均数一种,好学的小聪通过网络搜索,又得到了两种平均数的定义,他把三种平均数的定义整理如下:
对于两个数a,b,
称为a,b这两个数的算术平均数,
称为a,b这两个数的几何平均数,
称为a,b这两个数的平方平均数.
小聪根据上述定义,探究了一些问题,下面是他的探究过程,请你补充完整:
(1) 若a=-1, b=-2, 则M= , N= , P= ;
(2)小聪发现当a,b两数异号时,在实数范围内N没有意义,所以决定只研究当a,b都是正数时这三种平均数的大小关系.结合乘法公式和勾股定理的学习经验,他选择构造几何图形,用面积法解决问题:如图,画出边长为a+b的正方形和它的两条对角线,则图1中阴影部分的面积可以表示 N .
①请分别在图2,图3中用阴影标出一个面积为M ,P 的图形;
②借助图形可知当a,b都是正数时,M,N,P的大小关系是: (把M,N,P从小到大排列,并用“<”或“≤”号连接).
26.在平面直角坐标系xOy中,若P,Q为某个矩形不相邻的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.图1为点P,Q的“相关矩形”的示意图.
已知点A的坐标为(1,2)
(1) 如图2, 点B的坐标为(b,0).
①若b=-2, 则点A, B的“相关矩形”的面积是 ;
②若点A,B的“相关矩形”的面积是8,则b的值为 .
(2) 如图3, 点C在过点( 且平行x轴的直线l上,若点A,C的“相关矩形”是正方形,直接写出点C 的坐标;
(3)如图4,等边△DEF的边DE在x轴上,顶点F 在y轴的正半轴上,点D的坐标为(1,0),点M 的坐标为(m,2),若在△DEF的边上存在一点N,使得点M,N的“相关矩形”为正方形,请直接写出m的取值范围.
同课章节目录
