第二章_一元二次方程_易错题集(含答案)2025-2026学年北师大版九年级数学上册
文档属性
| 名称 | 第二章_一元二次方程_易错题集(含答案)2025-2026学年北师大版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 154.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 07:35:44 | ||
图片预览




文档简介
第二章 一元二次方程 易错题集 2025-2026学年北师大版九年级数学上册
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题(本题共计 10 小题 ,每题 3 分 ,共计30分 ,)
1.一元二次方程的解为( )
A. B. C.或 D.且
2.下列一元二次方程无实数根的是( )
A. B. C. D.
3.,则
A. B. C.或 D.或
4.若关于的一元二次方程有一个根是,则的值是( )
A. B. C. D.–或
5.已知关于的一元二次方程有两根为和,则的值是( )
A. B. C. D.
6.用配方法解一元二次方程,配方正确的是( )
A. B. C. D.
7.某兴趣学习小组组织一次围棋比赛,参赛的每两人之间都要比赛一场,按计划需要进行场比赛,则参赛的人数为( )
A.人 B.人 C.人 D.人
8.已知是一元二次方程的一个根,则的值为( )
A.或 B. C. D.
9.已知,是方程的两个实数根,则的值是( )
A. B. C. D.
10.如图,在矩形中,,.以点为圆心,的长为半径画弧,交于点,交于点.下列哪条线段的长度是方程的一个根( )
A.线段的长 B.线段的长 C.线段的长 D.线段的长
二、 填空题(本题共计 5 小题 ,每题 3 分 ,共计15分 ,)
11.方程的根是________.
12.某驻村工作队为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为的矩形养鸡场,如图所示,鸡场一面靠墙,墙长,另外三面用长的篱笆围成,其中一边开有一扇宽的门(不包括篱笆),其他区域均密闭,则这个鸡场的长是________,宽是________.
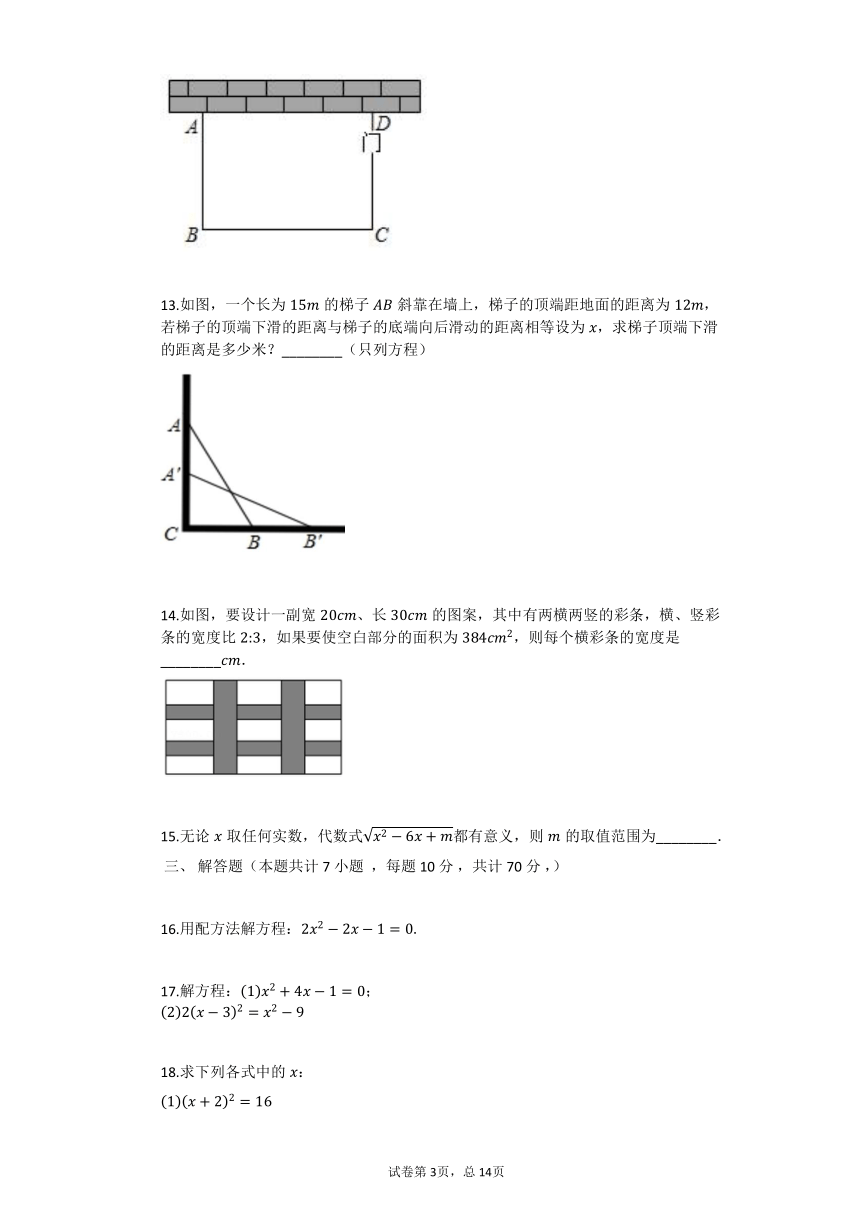
13.如图,一个长为的梯子斜靠在墙上,梯子的顶端距地面的距离为,若梯子的顶端下滑的距离与梯子的底端向后滑动的距离相等设为,求梯子顶端下滑的距离是多少米?________(只列方程)
14.如图,要设计一副宽、长的图案,其中有两横两竖的彩条,横、竖彩条的宽度比,如果要使空白部分的面积为,则每个横彩条的宽度是________.
15.无论取任何实数,代数式都有意义,则的取值范围为________.
三、 解答题(本题共计 7 小题 ,每题 10 分 ,共计70分 ,)
16.用配方法解方程:
17.解方程:;
18.求下列各式中的:
19.解方程:
;
;
;
.
20.已知关于的一元二次方程.
若方程有不相等实数根,求的取值范围;
若方程有两个相等实数根,求此时方程的根.
21.学校计划利用一片空地建一个长方形电动车车棚,其中一面靠墙,墙的长度为米,在与墙平行的一面开一个米宽的门.已知现有的木板材料可新建的总长为米,且全部用于除墙外其余三面外墙的修建.
长方形车棚与墙垂直的一面至少为多少米?
为了方便学生通行,施工单位决定在车棚内修建几条等宽的小路(如图中阴影),若车棚与墙垂直的一面长按(1)中的最小长度,则停放电动车的区域面积能否达到平方米,若能,此时小路的宽度是多少米?若不能,请说明理由.
22.某学校的学生进行综合实践活动时,探究每盆植株培育株数与市场销售价格之间的关系,通过实验和市场调查发现,每盆植株在株以内(含株),植株的品质较高,单株售价元,超过株后,每盆每多种株,单株售价降低元,当每盆种植株株数超过株后,植株品质较低,市场统一收购价单株元,每盆最多可种植株.
设每盆种植株,
①则单株售价________元,每盆售价________元(用含的代数式表示);
②当每盆售价为元时,求的值.
该学生实验小组共种植了盆,每盆培育所需费用(元)与每盆种植株数(株)之间满足,
每盆植株除培育费用外无其他支出.该小组将其中盆赠送给学校,其余放至市场出售,全部售出后销售所得扣除培育费用后还剩余元,求每盆的种植株数.
参考答案与试题解析
第二章 一元二次方程 易错题集 2025-2026学年北师大版九年级数学上册
一、 选择题(本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【考点】
解一元二次方程-因式分解法
【解析】
此题暂无解析
【解答】
C
2.
【答案】
C
【考点】
根的判别式
【解析】
此题暂无解析
【解答】
【详解】解:、 ,则该方程有两个不相等的实数根,故本选项不符合题意;
B、 ,则该方程有两个不相等的实数根,故本选项不符合题意;
C、,则该方程无实数根,故本选项符合题意;
D、,则该方程有两个相等的实数根,故本选项不符合题意;
故选:.
3.
【答案】
A
【考点】
换元法解一元二次方程
【解析】
解答此题的关键在于理解换元法的相关知识,掌握换元法是中学数学中的一个重要的数学思想,其应用非常广泛,当分式方程具有某种特殊形式,一般的去分母不易解决时,可考虑用换元法.
【解答】
解:设,由原方程,得,
整理,得,
解得或(舍去),
所以.
故选:.
4.
【答案】
A
【考点】
一元二次方程的解
【解析】
此题暂无解析
【解答】
A
5.
【答案】
B
【考点】
根与系数的关系
【解析】
此题暂无解析
【解答】
B
6.
【答案】
A
【考点】
解一元二次方程-配方法
【解析】
先移项并把二次项系数化为,得出 ,在方程的两边同时加上一次项系数一半的平方,左边写成完全平方式即得.
【解答】
A
7.
【答案】
B
【考点】
一元二次方程的应用——其他问题
【解析】
此题暂无解析
【解答】
设参赛的人数为人.
根据题意,得,
解得(不合题意,舍去)所以参赛的人数为人.
故选.
8.
【答案】
B
【考点】
一元二次方程的定义
一元二次方程的解
【解析】
此题暂无解析
【解答】
【详解】解:把代入得:
解得:
∵ 是一元二次方程,
∴
∴
∴
故选:.
9.
【答案】
A
【考点】
根与系数的关系
一元二次方程的解
【解析】
此题暂无解析
【解答】
A
10.
【答案】
B
【考点】
勾股定理
矩形的性质
解一元二次方程-公式法
【解析】
由方程的解结合线段的和差可以得到答案.
【解答】
解:∵ ,
∴ ,
∴ .
∵ ,,,
∴ ,
∴ ,
∴ ,.
∵ ,
∴ ,
∴ 线段的长是的根.
故选.
二、 填空题(本题共计 5 小题 ,每题 3 分 ,共计15分 )
11.
【答案】
【考点】
解一元二次方程-因式分解法
【解析】
此题暂无解析
【解答】
12.
【答案】
,
【考点】
一元二次方程的应用——几何图形面积问题
【解析】
此题暂无解析
【解答】
故答案为:;.
13.
【答案】
【考点】
一元二次方程的应用——其他问题
【解析】
此题暂无解析
【解答】
14.
【答案】
【考点】
一元二次方程的应用
一元二次方程的应用——几何图形面积问题
【解析】
此题暂无解析
【解答】
15.
【答案】
【考点】
二次根式有意义的条件
非负数的性质:偶次方
配方法的应用
【解析】
二次根式的被开方数是非负数,即,所以.通过偶次方是非负数可求得,则易求的取值范围.
【解答】
解:由题意,得
,即,
∵ ,要使得恒大于等于,
∴ ,
∴ ,
故答案为:.
三、 解答题(本题共计 7 小题 ,每题 10 分 ,共计70分 )
16.
【答案】
解: ,
,
,
,
,
,
∴ ,.
【考点】
解一元二次方程-配方法
【解析】
此题暂无解析
【解答】
解: ,
,
,
,
,
,
∴ ,.
17.
【答案】
【解答】解:()∵ ,
∴ ,
∴ ,
∴ ,
∴ .
(2)∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ 或,
∴ ,
【考点】
解一元二次方程-配方法
解一元二次方程-因式分解法
【解析】
此题暂无解析
【解答】
【解答】解:()∵ ,
∴ ,
∴ ,
∴ ,
∴ .
(2)∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ 或,
∴ ,
18.
【答案】
解:(1)或,或.
(2)
【考点】
解一元二次方程-直接开平方法
立方根的性质
【解析】
此题暂无解析
【解答】
解:(1)或,或.
(2)
19.
【答案】
解:()分解因式得: ,
可得或,
解得: ;
(2)∵ ,
∴ ,
则或,
解得: ;
(3),
,
∴ ,
∴ ,
解得: ;
(4) ,
,
,
或,
.
【考点】
解一元二次方程-因式分解法
解一元二次方程-公式法
【解析】
此题暂无解析
【解答】
解:()分解因式得: ,
可得或,
解得: ;
(2)∵ ,
∴ ,
则或,
解得: ;
(3),
,
∴ ,
∴ ,
解得: ;
(4) ,
,
,
或,
.
20.
【答案】
解: ,
, ,,
:一元二次方程有不相等实数根,
∴ ,
解得 ,
又∵ 得,
∴ 且.
一元二次方程有两个相等得实数根,
∴ ,
解得 ,
∴ 方程为 ,
解得 .
【考点】
一元二次方程的定义
根的判别式
一元二次方程的解
【解析】
此题暂无解析
【解答】
解: ,
, ,,
:一元二次方程有不相等实数根,
∴ ,
解得 ,
又∵ 得,
∴ 且.
一元二次方程有两个相等得实数根,
∴ ,
解得 ,
∴ 方程为 ,
解得 .
21.
【答案】
解:(1)设与墙垂直的一面为米,另一面则为米,
根据题意得: ,解得: ,
答:长方形车棚与墙垂直的一面至少米;
(2)设小路的宽为米,根据题意得,
,
整理得: ,
解得: (舍去), ,
答:小路的宽为米.
【考点】
一元一次不等式的实际应用
一元二次方程的应用——几何图形面积问题
【解析】
此题暂无解析
【解答】
解:(1)设与墙垂直的一面为米,另一面则为米,
根据题意得: ,解得: ,
答:长方形车棚与墙垂直的一面至少米;
(2)设小路的宽为米,根据题意得,
,
整理得: ,
解得: (舍去), ,
答:小路的宽为米.
22.
【答案】
解:()①设每盆种植株,
单株售价为,
每盆售价,
故答案为: ;
②令的值为,则,
解得,
答:当每盆售价为元时,或.
(2)时,
整理得(舍去),
当时,,
化简,整理得(舍去),
当时,,
解得,
综上所述,每盆种植株或株时,还剩余元.
【考点】
列代数式
一元二次方程的应用——其他问题
由实际问题抽象出一元二次方程
【解析】
此题暂无解析
【解答】
解:()①设每盆种植株,
单株售价为,
每盆售价,
故答案为: ;
②令的值为,则,
解得,
答:当每盆售价为元时,或.
(2)时,
整理得(舍去),
当时,,
化简,整理得(舍去),
当时,,
解得,
综上所述,每盆种植株或株时,还剩余元.
试卷第4页,总9页
试卷第5页,总9页
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题(本题共计 10 小题 ,每题 3 分 ,共计30分 ,)
1.一元二次方程的解为( )
A. B. C.或 D.且
2.下列一元二次方程无实数根的是( )
A. B. C. D.
3.,则
A. B. C.或 D.或
4.若关于的一元二次方程有一个根是,则的值是( )
A. B. C. D.–或
5.已知关于的一元二次方程有两根为和,则的值是( )
A. B. C. D.
6.用配方法解一元二次方程,配方正确的是( )
A. B. C. D.
7.某兴趣学习小组组织一次围棋比赛,参赛的每两人之间都要比赛一场,按计划需要进行场比赛,则参赛的人数为( )
A.人 B.人 C.人 D.人
8.已知是一元二次方程的一个根,则的值为( )
A.或 B. C. D.
9.已知,是方程的两个实数根,则的值是( )
A. B. C. D.
10.如图,在矩形中,,.以点为圆心,的长为半径画弧,交于点,交于点.下列哪条线段的长度是方程的一个根( )
A.线段的长 B.线段的长 C.线段的长 D.线段的长
二、 填空题(本题共计 5 小题 ,每题 3 分 ,共计15分 ,)
11.方程的根是________.
12.某驻村工作队为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为的矩形养鸡场,如图所示,鸡场一面靠墙,墙长,另外三面用长的篱笆围成,其中一边开有一扇宽的门(不包括篱笆),其他区域均密闭,则这个鸡场的长是________,宽是________.
13.如图,一个长为的梯子斜靠在墙上,梯子的顶端距地面的距离为,若梯子的顶端下滑的距离与梯子的底端向后滑动的距离相等设为,求梯子顶端下滑的距离是多少米?________(只列方程)
14.如图,要设计一副宽、长的图案,其中有两横两竖的彩条,横、竖彩条的宽度比,如果要使空白部分的面积为,则每个横彩条的宽度是________.
15.无论取任何实数,代数式都有意义,则的取值范围为________.
三、 解答题(本题共计 7 小题 ,每题 10 分 ,共计70分 ,)
16.用配方法解方程:
17.解方程:;
18.求下列各式中的:
19.解方程:
;
;
;
.
20.已知关于的一元二次方程.
若方程有不相等实数根,求的取值范围;
若方程有两个相等实数根,求此时方程的根.
21.学校计划利用一片空地建一个长方形电动车车棚,其中一面靠墙,墙的长度为米,在与墙平行的一面开一个米宽的门.已知现有的木板材料可新建的总长为米,且全部用于除墙外其余三面外墙的修建.
长方形车棚与墙垂直的一面至少为多少米?
为了方便学生通行,施工单位决定在车棚内修建几条等宽的小路(如图中阴影),若车棚与墙垂直的一面长按(1)中的最小长度,则停放电动车的区域面积能否达到平方米,若能,此时小路的宽度是多少米?若不能,请说明理由.
22.某学校的学生进行综合实践活动时,探究每盆植株培育株数与市场销售价格之间的关系,通过实验和市场调查发现,每盆植株在株以内(含株),植株的品质较高,单株售价元,超过株后,每盆每多种株,单株售价降低元,当每盆种植株株数超过株后,植株品质较低,市场统一收购价单株元,每盆最多可种植株.
设每盆种植株,
①则单株售价________元,每盆售价________元(用含的代数式表示);
②当每盆售价为元时,求的值.
该学生实验小组共种植了盆,每盆培育所需费用(元)与每盆种植株数(株)之间满足,
每盆植株除培育费用外无其他支出.该小组将其中盆赠送给学校,其余放至市场出售,全部售出后销售所得扣除培育费用后还剩余元,求每盆的种植株数.
参考答案与试题解析
第二章 一元二次方程 易错题集 2025-2026学年北师大版九年级数学上册
一、 选择题(本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【考点】
解一元二次方程-因式分解法
【解析】
此题暂无解析
【解答】
C
2.
【答案】
C
【考点】
根的判别式
【解析】
此题暂无解析
【解答】
【详解】解:、 ,则该方程有两个不相等的实数根,故本选项不符合题意;
B、 ,则该方程有两个不相等的实数根,故本选项不符合题意;
C、,则该方程无实数根,故本选项符合题意;
D、,则该方程有两个相等的实数根,故本选项不符合题意;
故选:.
3.
【答案】
A
【考点】
换元法解一元二次方程
【解析】
解答此题的关键在于理解换元法的相关知识,掌握换元法是中学数学中的一个重要的数学思想,其应用非常广泛,当分式方程具有某种特殊形式,一般的去分母不易解决时,可考虑用换元法.
【解答】
解:设,由原方程,得,
整理,得,
解得或(舍去),
所以.
故选:.
4.
【答案】
A
【考点】
一元二次方程的解
【解析】
此题暂无解析
【解答】
A
5.
【答案】
B
【考点】
根与系数的关系
【解析】
此题暂无解析
【解答】
B
6.
【答案】
A
【考点】
解一元二次方程-配方法
【解析】
先移项并把二次项系数化为,得出 ,在方程的两边同时加上一次项系数一半的平方,左边写成完全平方式即得.
【解答】
A
7.
【答案】
B
【考点】
一元二次方程的应用——其他问题
【解析】
此题暂无解析
【解答】
设参赛的人数为人.
根据题意,得,
解得(不合题意,舍去)所以参赛的人数为人.
故选.
8.
【答案】
B
【考点】
一元二次方程的定义
一元二次方程的解
【解析】
此题暂无解析
【解答】
【详解】解:把代入得:
解得:
∵ 是一元二次方程,
∴
∴
∴
故选:.
9.
【答案】
A
【考点】
根与系数的关系
一元二次方程的解
【解析】
此题暂无解析
【解答】
A
10.
【答案】
B
【考点】
勾股定理
矩形的性质
解一元二次方程-公式法
【解析】
由方程的解结合线段的和差可以得到答案.
【解答】
解:∵ ,
∴ ,
∴ .
∵ ,,,
∴ ,
∴ ,
∴ ,.
∵ ,
∴ ,
∴ 线段的长是的根.
故选.
二、 填空题(本题共计 5 小题 ,每题 3 分 ,共计15分 )
11.
【答案】
【考点】
解一元二次方程-因式分解法
【解析】
此题暂无解析
【解答】
12.
【答案】
,
【考点】
一元二次方程的应用——几何图形面积问题
【解析】
此题暂无解析
【解答】
故答案为:;.
13.
【答案】
【考点】
一元二次方程的应用——其他问题
【解析】
此题暂无解析
【解答】
14.
【答案】
【考点】
一元二次方程的应用
一元二次方程的应用——几何图形面积问题
【解析】
此题暂无解析
【解答】
15.
【答案】
【考点】
二次根式有意义的条件
非负数的性质:偶次方
配方法的应用
【解析】
二次根式的被开方数是非负数,即,所以.通过偶次方是非负数可求得,则易求的取值范围.
【解答】
解:由题意,得
,即,
∵ ,要使得恒大于等于,
∴ ,
∴ ,
故答案为:.
三、 解答题(本题共计 7 小题 ,每题 10 分 ,共计70分 )
16.
【答案】
解: ,
,
,
,
,
,
∴ ,.
【考点】
解一元二次方程-配方法
【解析】
此题暂无解析
【解答】
解: ,
,
,
,
,
,
∴ ,.
17.
【答案】
【解答】解:()∵ ,
∴ ,
∴ ,
∴ ,
∴ .
(2)∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ 或,
∴ ,
【考点】
解一元二次方程-配方法
解一元二次方程-因式分解法
【解析】
此题暂无解析
【解答】
【解答】解:()∵ ,
∴ ,
∴ ,
∴ ,
∴ .
(2)∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ 或,
∴ ,
18.
【答案】
解:(1)或,或.
(2)
【考点】
解一元二次方程-直接开平方法
立方根的性质
【解析】
此题暂无解析
【解答】
解:(1)或,或.
(2)
19.
【答案】
解:()分解因式得: ,
可得或,
解得: ;
(2)∵ ,
∴ ,
则或,
解得: ;
(3),
,
∴ ,
∴ ,
解得: ;
(4) ,
,
,
或,
.
【考点】
解一元二次方程-因式分解法
解一元二次方程-公式法
【解析】
此题暂无解析
【解答】
解:()分解因式得: ,
可得或,
解得: ;
(2)∵ ,
∴ ,
则或,
解得: ;
(3),
,
∴ ,
∴ ,
解得: ;
(4) ,
,
,
或,
.
20.
【答案】
解: ,
, ,,
:一元二次方程有不相等实数根,
∴ ,
解得 ,
又∵ 得,
∴ 且.
一元二次方程有两个相等得实数根,
∴ ,
解得 ,
∴ 方程为 ,
解得 .
【考点】
一元二次方程的定义
根的判别式
一元二次方程的解
【解析】
此题暂无解析
【解答】
解: ,
, ,,
:一元二次方程有不相等实数根,
∴ ,
解得 ,
又∵ 得,
∴ 且.
一元二次方程有两个相等得实数根,
∴ ,
解得 ,
∴ 方程为 ,
解得 .
21.
【答案】
解:(1)设与墙垂直的一面为米,另一面则为米,
根据题意得: ,解得: ,
答:长方形车棚与墙垂直的一面至少米;
(2)设小路的宽为米,根据题意得,
,
整理得: ,
解得: (舍去), ,
答:小路的宽为米.
【考点】
一元一次不等式的实际应用
一元二次方程的应用——几何图形面积问题
【解析】
此题暂无解析
【解答】
解:(1)设与墙垂直的一面为米,另一面则为米,
根据题意得: ,解得: ,
答:长方形车棚与墙垂直的一面至少米;
(2)设小路的宽为米,根据题意得,
,
整理得: ,
解得: (舍去), ,
答:小路的宽为米.
22.
【答案】
解:()①设每盆种植株,
单株售价为,
每盆售价,
故答案为: ;
②令的值为,则,
解得,
答:当每盆售价为元时,或.
(2)时,
整理得(舍去),
当时,,
化简,整理得(舍去),
当时,,
解得,
综上所述,每盆种植株或株时,还剩余元.
【考点】
列代数式
一元二次方程的应用——其他问题
由实际问题抽象出一元二次方程
【解析】
此题暂无解析
【解答】
解:()①设每盆种植株,
单株售价为,
每盆售价,
故答案为: ;
②令的值为,则,
解得,
答:当每盆售价为元时,或.
(2)时,
整理得(舍去),
当时,,
化简,整理得(舍去),
当时,,
解得,
综上所述,每盆种植株或株时,还剩余元.
试卷第4页,总9页
试卷第5页,总9页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
