阶段质量评价(四) 统计(含解析)高中数学苏教版(2019)选择性必修第二册
文档属性
| 名称 | 阶段质量评价(四) 统计(含解析)高中数学苏教版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 109.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 00:00:00 | ||
图片预览




文档简介
阶段质量评价(四) 统 计
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有一项是符合题目要求的)
1.下列两个变量中能够具有相关关系的是 ( )
A.人所站的高度与视野
B.人眼的近视程度与身高
C.正方体的体积与棱长
D.某同学的学籍号与考试成绩
2.设变量X和变量Y的相关系数为r1,变量U和变量V的相关系数为r2,且r1=-0.734,r2=0.984,则 ( )
A.X和Y之间呈正线性相关关系,且X和Y的线性相关程度强于U和V的线性相关程度
B.X和Y之间呈负线性相关关系,且X和Y的线性相关程度强于U和V的线性相关程度
C.U和V之间呈负线性相关关系,且X和Y的线性相关程度弱于U和V的线性相关程度
D.U和V之间呈正线性相关关系,且X和Y的线性相关程度弱于U和V的线性相关程度
3.变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,2),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的相关系数,r2表示变量V与U之间的相关系数,则 ( )
A.r2C.r2<04.下列关于独立性检验的说法正确的是 ( )
A.独立性检验是对两个变量是否具有线性相关关系的一种检验
B.独立性检验可以100%确定两个变量之间是否具有某种关系
C.利用χ2独立性检验推断吸烟与患肺病的关联中,有99%的把握认为吸烟与患肺病有关系时,则我们可以说在100个吸烟的人中,有99人患肺病
D.对于独立性检验,随机变量χ2的值越小,“两变量有关系”的概率越小
5.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+1上,则这组样本数据的相关系数为 ( )
A.-1 B.-
C. D.1
6.在下列各图中,两个变量具有线性相关关系的是 ( )
7.某校团委对“学生性别和喜欢某个APP是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢的人数占男生人数的,女生喜欢的人数占女生人数的,若有95%的把握认为是否喜欢和性别有关,则调查人数中男生可能有 ( )
P(χ2≥x0) 0.050 0.010
x0 3.841 6.635
附:χ2=.
A.30人 B.54人
C.60人 D.75人
8.用模型y=aekx拟合一组数(xi,yi)(i=1,2,…,2 024),若x1+x2+…+x2 024=2 024,y1y2…y2 024=e20 240,设z=ln y,变换后的线性回归方程为=bx+6,则ak= ( )
A.20 240 B.6e4
C.4e6 D.2 024
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.某厂近几年陆续购买了几台 A 型机床,该型机床已投入生产的时间x(单位:年)与当年所需要支出的维修费用y(单位:万元)有如下统计资料:
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7
根据表中的数据可得到线性回归方程为y=1.23x+,则 ( )
A.=0.08
B.y与x的相关系数r>0
C.表中维修费用的60百分位数为6
D.该型机床已投入生产的时间为 10年时,当年所需要支出的维修费用一定是12.38万元
10.某校有在校学生900人,其中男生400人,女生500人,为了解该校学生对学校课后延时服务的满意度,随机调查了40名男生和50名女生.每位被调查的学生都对学校的课后延时服务给出了满意或不满意的评价,统计过程中发现随机从这90人中抽取一人,此人评价为满意的概率为.在制定2×2列联表时,由于某些因素缺失了部分数据,而获得如下2×2列联表,下列结论正确的是 ( )
满意 不满意 合计
男 10
女
合计 90
参考公式与临界值表:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.100 0.050 0.025 0.010 0.001
x0 2.706 3.841 5.024 6.635 10.828
A.满意度的调查过程采用了分层抽样的抽样方法
B.50名女生中对课后延时服务满意的人数为20
C.χ2的观测值为9
D.根据独立性检验,不能认为“对课后延时服务的满意度与性别有关系”
11.下列说法中,正确的是 ( )
A.一组数据10,11,11,12,13,14,16,18,20,22的40百分位数为12
B.若样本数据2x1+1,2x2+1,…,2x10+1的方差为8,则数据x1,x2,…,x10的方差为2
C.已知随机变量X服从正态分布N(μ,σ2),若P(X≥-2)+P(X≥6)=1,则μ=2
D.在独立性检验中,提出假设H0:分类变量X和Y独立.当χ2≤x0时,我们就推断H0不成立,即认为X和Y不独立;当χ2>x0时,我们没有充分证据推断H0不成立,可以认为X和Y独立
三、填空题(本大题共3小题,每小题5分,共15分.把答案填在题中的横线上)
12.甲、乙、丙、丁各自研究两个随机变量的数据,若甲、乙、丙、丁计算得到各自研究的两个随机变量的相关系数分别为r1=0.66,r2=-0.97,r3=0.92,r4=0.89,则这四人中, 研究的两个随机变量的线性相关程度最高.
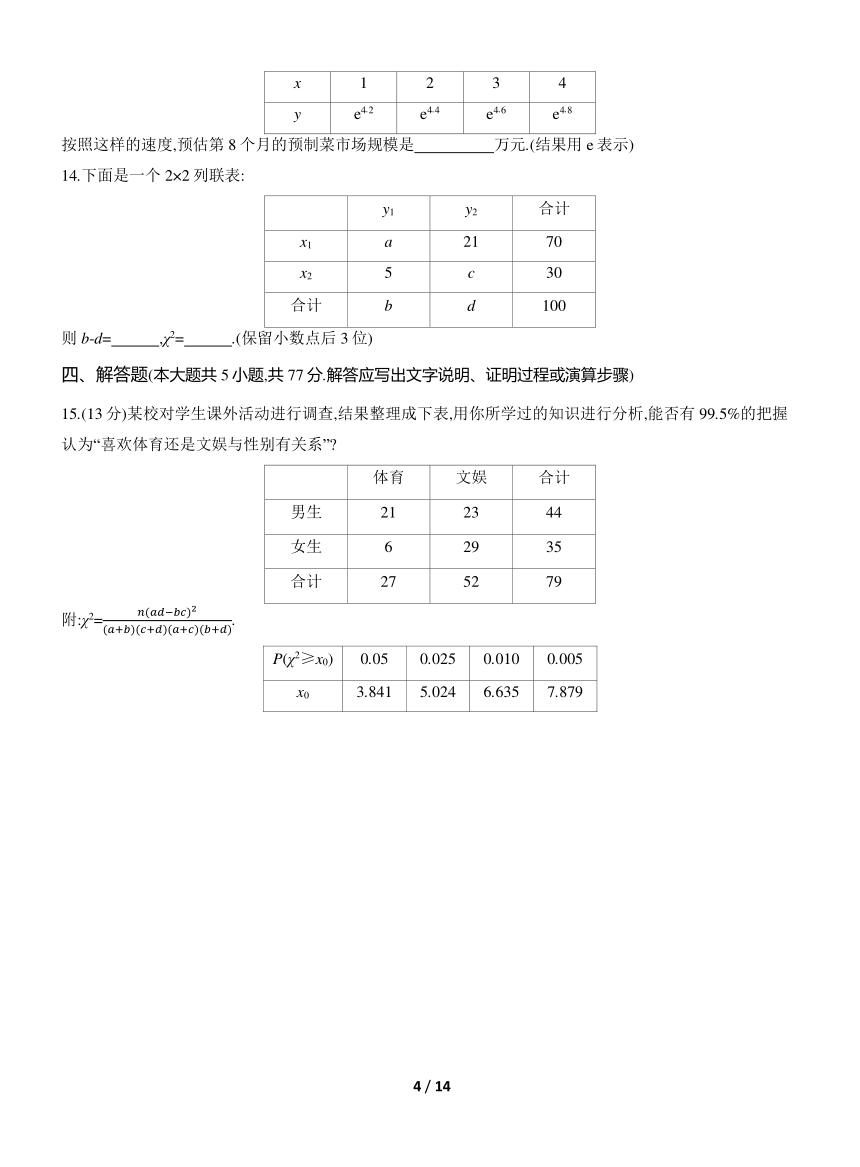
13.预制菜指以农、畜、禽、水产品为原辅料,配以调味料等经预选、调制等工艺加工而成的半成品.近几年预制菜市场快速增长.某城市调查近4个月的预制菜市场规模y(万元)得到如表所示的数据,根据数据得到y关于x的非线性回归方程=.
x 1 2 3 4
y e4.2 e4.4 e4.6 e4.8
按照这样的速度,预估第8个月的预制菜市场规模是 万元.(结果用e表示)
14.下面是一个2×2列联表:
y1 y2 合计
x1 a 21 70
x2 5 c 30
合计 b d 100
则b-d= ,χ2= .(保留小数点后3位)
四、解答题(本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)某校对学生课外活动进行调查,结果整理成下表,用你所学过的知识进行分析,能否有99.5%的把握认为“喜欢体育还是文娱与性别有关系”
体育 文娱 合计
男生 21 23 44
女生 6 29 35
合计 27 52 79
附:χ2=.
P(χ2≥x0) 0.05 0.025 0.010 0.005
x0 3.841 5.024 6.635 7.879
16.(15分)随着科技发展的日新月异,人工智能融入了各个行业,促进了社会的快速发展.其中利用人工智能生成的虚拟角色因为拥有更低的人工成本,正逐步取代传统的真人直播带货.某公司使用虚拟角色直播带货销售金额得到逐步提升,以下为该公司自2023年8月使用虚拟角色直播带货后的销售金额情况统计.
年月 2023年 8月 2023年 9月 2023年 10月 2023年 11月 2023年 12月 2024年 1月
月份编号x 1 2 3 4 5 6
销售金额 y/万元 15.4 25.4 35.4 85.4 155.4 195.4
若y与x的相关关系拟用线性回归模型表示,回答如下问题:
(1)试求变量y与x的相关系数r(结果精确到0.01);
(2)试求y关于x的线性回归方程,并据此预测2024年2月份该公司的销售金额.(均保留一位小数)
参考数据:xiyi=2 463.4,=20.
.
17.(15分)数独是源自18世纪瑞士的一种数学游戏,玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(3×3)内的数字均含1~9,且不重复.数独爱好者小明打算报名参加“丝路杯”全国数独大赛初级组的比赛.
(1)赛前小明进行了一段时间的训练,每天解题的平均速度y(秒/题)与训练天数x(天)有关,经统计得到如下数据:
x(天) 1 2 3 4 5 6 7
y(秒/题) 910 800 600 440 300 240 210
现用=+作为回归方程模型,请利用表中数据,求出该回归方程;(用分数表示)
(2)小明和小红玩“对战赛”,每局两人同时开始解一道数独题,先解出题的人获胜,不存在平局,两人约定先胜3局者赢得比赛.若小明每局获胜的概率为,且各局之间相互独立,设比赛X局后结束,求随机变量X的分布列及均值.
参考数据:
tiyi t-72
1 750 0.37 0.55
参考公式:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其线性回归方程=+μ的斜率和截距的最小二乘估计分别为= ,=-.
18.(17分)我国风云系列卫星可以监测气象和国土资源情况.某地区水文研究人员为了了解汛期人工测雨量x(单位:dm)与遥测雨量y(单位:dm)的关系,统计得到该地区10组雨量数据如表:
样本号i 1 2 3 4 5 6 7 8 9 10
人工测 雨量xi 5.38 7.99 6.37 6.71 7.53 5.53 4.18 4.04 6.02 4.23
遥测雨 量yi 5.43 8.07 6.57 6.14 7.95 5.56 4.27 4.15 6.04 4.49
|xi-yi| 0.05 0.08 0.2 0.57 0.42 0.03 0.09 0.11 0.02 0.26
并计算得≈353.6,≈361.7,xiyi≈357.3,≈33.62,≈34.42, ≈34.02.
(1)求该地区汛期遥测雨量y与人工测雨量x的相关系数(精确到0.01),并判断它们是否具有线性相关关系;
(2)规定:数组(xi,yi)满足|xi-yi|<0.1为“Ⅰ类误差”;满足0.1≤|xi-yi|<0.3为“Ⅱ类误差”;满足|xi-yi|≥0.3为“Ⅲ类误差”.为进一步研究,该地区水文研究人员从“Ⅰ类误差”“Ⅱ类误差”中随机抽取3组数据与“Ⅲ类误差”数据进行对比,记抽到“Ⅰ类误差”的数据的组数为X,求X的概率分布与数学期望.
附:相关系数r=,≈17.4.
19.(17分)为考察药物M对预防疾病A以及药物N对治疗疾病A的效果,科研团队进行了大量动物对照试验.根据100个简单随机样本的数据,得到如下列联表:(单位:只)
药物M 疾病A 合计
未患病 患病
未服用 30 15 45
服用 45 10 55
合计 75 25 100
(1)根据表中所给数据,判断能否有99%的把握认为药物M对预防疾病A有效果;
(2)用频率估计概率,现从患病的动物中用随机抽样的方法每次选取1只,用药物N进行治疗.已知药物N的治愈率如下:对未服用过药物M的动物治愈率为,对服用过药物M的动物治愈率为.若共选取3次,每次选取的结果是相互独立的.记选取的3只动物中被治愈的动物个数为X,求X的分布列和数学期望.
阶段质量评价(四)
1.选A 人所站的高度越高则视野越开阔,具有正相关关系,故A正确;人眼的近视程度与身高不具有相关关系,故B错误;正方体的体积与棱长是一种确定关系,故C错误;某同学的学籍号与考试成绩不具有相关关系,故D错误.故选A.
2.选D 由相关系数r1=-0.734<0,可知变量X与Y之间呈负线性相关关系,由相关系数r2=0.984>0,可知变量U与V之间呈正线性相关关系,又|r1|<|r2|,所以变量U与V的线性相关程度比变量X与Y的线性相关程度强.故选D.
3.选C Y随X的增大而增大,故变量Y与X正相关,即r1>0;V随U的增大而减小,故变量V与U负相关,即r2<0,故r2<04.选D 对于A,独立性检验是通过卡方计算来判断两个变量存在关联的可能性的一种方法,并非检验二者是否是线性相关,故错误;对于B,独立性检验并不能100%确定两个变量相关,故错误;对于C,99%是指“吸烟”和“患肺病”存在关联的可能性,并非吸烟人中患肺病的发病率,故错误;对于D,根据卡方计算的定义可知该选项正确.故选D.
5.选A 因为所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+1上,所以它们负相关,相关系数为-1.故选A.
6.选C 对于A,两个变量为函数关系,不是线性相关关系,故A错误;对于B,所有点不是在一条直线附近波动,不是线性相关关系,故B错误;对于C,对于两个变量x,y,y随着x的增加而减少,且所有点都在一条直线附近波动,所以具有线性相关关系,故C正确;对于D,两个变量不具有相关性,故D错误.故选C.
7.选BC 设男生的人数为6n(n∈N*),
根据题意列出2×2列联表如下表所示:
男生 女生 合计
喜欢 5n 4n 9n
不喜欢 n 2n 3n
合计 6n 6n 12n
则χ2==,
由于有95%的把握认为是否喜欢和性别有关,则3.841<χ2≤6.635,即3.841<≤6.635,得8.642 3因为n∈N*,则n的可能取值有9,10,11,12,13,14,因此,调查人数中男生人数的可能值为54,60,66,72,78,84.故选BC.
8.选C 由条件可知=1,=ln yi=10,代入=bx+6 b=4,则z=ln y=ln a+kx=4x+6 k=4,a=e6,故C正确.故选C.
9.选ABC 根据题意可得,=4,==5,所以样本中心点为(4,5).将样本中心点(4,5)代入线性回归方程y=1.23x+中,可得=0.08,故A正确;由表中数据可得y随着x增大而增大,x与y正相关,所以相关系数r>0,故B正确;维修费用从小到大依次为2.2,3.8,5.5,6.5,7,60百分位数为=6,故C正确;根据回归分析的概念,机床投入生产的时间为 10年时,所需要支出的维修费用大概是12.38万元,故D错误.故选ABC.
10.选AD 因为在校学生中有400名男生,500名女生,随机调查了40名男生和50名女生,男女比例始终是4∶5,所以采用了分层抽样的方法,故A正确;调查的90人中,对学校课后延时服务满意的人数为90×=60,其中男生满意的人数为40-10=30,所以女生满意的人数为30,女生不满意的人数为20,故B错误;由B选项的分析,补全列联表如下:
满意 不满意 合计
男 30 10 40
女 30 20 50
合计 60 30 90
由列联表可得χ2==,故C错误;提出假设H0:对课后延时服务的满意度与性别无关,由χ2=<10.828,没有充足的证据推断H0不成立,即不能认为“对课后延时服务的满意度与性别有关系”,故D正确.故选AD.
11.选BC 由于10,11,11,12,13,14,16,18,20,22共10个数据,且10×0.4=4,故40百分位数为第4,5个数据的平均数=12.5,故A错误;设数据x1,x2,…,x10的平均数为=,方差为s2=[++…+],则数据2x1+1,2x2+1,…,2x10+1的平均数为
'=
==2+1,
方差为=[++…+]=[++…+]=[++…+]=4s2=8,所以s2=2,故B正确;P(X≥-2)+P(X≥6)=1则P(X≥6)=1-P(X≥-2)=P(X≤-2),即P(X≥6)=P(X≤-2),由正态分布N(μ,σ2)的性质可得μ==2,故C正确;在独立性检验中,提出假设H0:分类变量X和Y独立.当χ2≥x0时,我们就推断H0不成立,即认为X和Y不独立;当χ212.解析:因为|r2|=0.97>|r3|>|r4|>|r1|,所以这四人中,乙研究的两个随机变量的线性相关程度最高.
答案:乙
13.解析:由题设,令z=ln =-a,则==,==,所以=-a a=-4,则z=ln =+4,所以x=8代入回归方程,则z=ln =5.6,可得=e5.6万元.
答案:e5.6
14.解析:补全2×2列联表:
y1 y2 合计
x1 49 21 70
x2 5 25 30
合计 54 46 100
所以b-d=54-46=8,χ2=≈24.047.
答案:8 24.047
15.解:提出假设
H0:喜欢体育还是文娱与性别没有关系.
因为a=21,b=23,c=6,d=29,n=79,
则χ2===8.106>7.879,
因为当H0成立时,χ2≥7.879的概率约为0.005,
所以我们有99.5%的把握认为喜欢体育还是文娱与性别有关系.
16.解: (1)==3.5,
==85.4,
-6=1+4+9+16+25+36-6×12.25=17.5,
所以r=
==≈0.96.
(2)由题意=
=≈38.3,
所以=85.4-38.3×3.5≈-48.7,
所以y关于x的线性回归方程为y=38.3x-48.7,
所以预测2024年2月份该公司的销售金额为y=38.3×7-48.7=219.4万元.
17.解: (1)因为=+,ti=,所以=+t.
因为==500,
所以====,
所以=-=500-×0.37=,
所以=+t,
所以所求回归方程为=+.
(2)随机变量X的所有可能取值为3,4,5,
则P(X=3)=+=,
P(X=4)=××+××=,
P(X=5)=××+××=.
所以随机变量X的概率分布为
X 3 4 5
P
E(X)=3×+4×+5×=.
18.解: (1)因为r=
=
≈=≈0.98,
所以该地区汛期遥测雨量与人工测雨量有很强的线性相关关系.
(2)依题意,“Ⅰ类误差”有5组,“Ⅱ类误差”有3组,“Ⅲ类误差”有2组.
若从“Ⅰ类误差”和“Ⅱ类误差”数据中抽取3组,抽到“Ⅰ类误差”的组数X的所有可能取值为0,1,2,3,
则P(X=0)==,P(X=1)==,
P(X=2)===,
P(X=3)===,
所以X的概率分布为
X 0 1 2 3
P
法一 E(X)=0×+1×+2×+3×=.
法二 因为X~H(3,5,8),所以E(X)==.
19.解:(1)提出假设
H0:药物M对预防疾病A无效果,
根据列联表中的数据,经计算得到
χ2==≈3.030>2.706,
因为当H0成立时,P(χ2≥2.706)≈0.1,所以有99%的把握认为药物M对预防疾病A有效果.
(2)设A表示药物N的治愈率,B1表示未服用过药物M,B2表示服用过药物M,
由题意可得P(B1)==0.6,P(B2)==0.4,且P(A|B1)=0.5,P(A|B2)=0.75,
P(A)=P(B1)×P(A|B1)+P(B2)×P(A|B2)=0.6×0.5+0.4×0.75=0.6,
所以药物N的治愈率P=0.6=,
则X~B,
所以P(X=0)==,
P(X=1)==,
P(X=2)==,P(X=3)==,
所以随机变量X的概率分布如下表所示:
X 0 1 2 3
P
E(X)=0×+1×+2×+3×=.
1 / 8
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有一项是符合题目要求的)
1.下列两个变量中能够具有相关关系的是 ( )
A.人所站的高度与视野
B.人眼的近视程度与身高
C.正方体的体积与棱长
D.某同学的学籍号与考试成绩
2.设变量X和变量Y的相关系数为r1,变量U和变量V的相关系数为r2,且r1=-0.734,r2=0.984,则 ( )
A.X和Y之间呈正线性相关关系,且X和Y的线性相关程度强于U和V的线性相关程度
B.X和Y之间呈负线性相关关系,且X和Y的线性相关程度强于U和V的线性相关程度
C.U和V之间呈负线性相关关系,且X和Y的线性相关程度弱于U和V的线性相关程度
D.U和V之间呈正线性相关关系,且X和Y的线性相关程度弱于U和V的线性相关程度
3.变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,2),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的相关系数,r2表示变量V与U之间的相关系数,则 ( )
A.r2
A.独立性检验是对两个变量是否具有线性相关关系的一种检验
B.独立性检验可以100%确定两个变量之间是否具有某种关系
C.利用χ2独立性检验推断吸烟与患肺病的关联中,有99%的把握认为吸烟与患肺病有关系时,则我们可以说在100个吸烟的人中,有99人患肺病
D.对于独立性检验,随机变量χ2的值越小,“两变量有关系”的概率越小
5.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+1上,则这组样本数据的相关系数为 ( )
A.-1 B.-
C. D.1
6.在下列各图中,两个变量具有线性相关关系的是 ( )
7.某校团委对“学生性别和喜欢某个APP是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢的人数占男生人数的,女生喜欢的人数占女生人数的,若有95%的把握认为是否喜欢和性别有关,则调查人数中男生可能有 ( )
P(χ2≥x0) 0.050 0.010
x0 3.841 6.635
附:χ2=.
A.30人 B.54人
C.60人 D.75人
8.用模型y=aekx拟合一组数(xi,yi)(i=1,2,…,2 024),若x1+x2+…+x2 024=2 024,y1y2…y2 024=e20 240,设z=ln y,变换后的线性回归方程为=bx+6,则ak= ( )
A.20 240 B.6e4
C.4e6 D.2 024
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.某厂近几年陆续购买了几台 A 型机床,该型机床已投入生产的时间x(单位:年)与当年所需要支出的维修费用y(单位:万元)有如下统计资料:
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7
根据表中的数据可得到线性回归方程为y=1.23x+,则 ( )
A.=0.08
B.y与x的相关系数r>0
C.表中维修费用的60百分位数为6
D.该型机床已投入生产的时间为 10年时,当年所需要支出的维修费用一定是12.38万元
10.某校有在校学生900人,其中男生400人,女生500人,为了解该校学生对学校课后延时服务的满意度,随机调查了40名男生和50名女生.每位被调查的学生都对学校的课后延时服务给出了满意或不满意的评价,统计过程中发现随机从这90人中抽取一人,此人评价为满意的概率为.在制定2×2列联表时,由于某些因素缺失了部分数据,而获得如下2×2列联表,下列结论正确的是 ( )
满意 不满意 合计
男 10
女
合计 90
参考公式与临界值表:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.100 0.050 0.025 0.010 0.001
x0 2.706 3.841 5.024 6.635 10.828
A.满意度的调查过程采用了分层抽样的抽样方法
B.50名女生中对课后延时服务满意的人数为20
C.χ2的观测值为9
D.根据独立性检验,不能认为“对课后延时服务的满意度与性别有关系”
11.下列说法中,正确的是 ( )
A.一组数据10,11,11,12,13,14,16,18,20,22的40百分位数为12
B.若样本数据2x1+1,2x2+1,…,2x10+1的方差为8,则数据x1,x2,…,x10的方差为2
C.已知随机变量X服从正态分布N(μ,σ2),若P(X≥-2)+P(X≥6)=1,则μ=2
D.在独立性检验中,提出假设H0:分类变量X和Y独立.当χ2≤x0时,我们就推断H0不成立,即认为X和Y不独立;当χ2>x0时,我们没有充分证据推断H0不成立,可以认为X和Y独立
三、填空题(本大题共3小题,每小题5分,共15分.把答案填在题中的横线上)
12.甲、乙、丙、丁各自研究两个随机变量的数据,若甲、乙、丙、丁计算得到各自研究的两个随机变量的相关系数分别为r1=0.66,r2=-0.97,r3=0.92,r4=0.89,则这四人中, 研究的两个随机变量的线性相关程度最高.
13.预制菜指以农、畜、禽、水产品为原辅料,配以调味料等经预选、调制等工艺加工而成的半成品.近几年预制菜市场快速增长.某城市调查近4个月的预制菜市场规模y(万元)得到如表所示的数据,根据数据得到y关于x的非线性回归方程=.
x 1 2 3 4
y e4.2 e4.4 e4.6 e4.8
按照这样的速度,预估第8个月的预制菜市场规模是 万元.(结果用e表示)
14.下面是一个2×2列联表:
y1 y2 合计
x1 a 21 70
x2 5 c 30
合计 b d 100
则b-d= ,χ2= .(保留小数点后3位)
四、解答题(本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)某校对学生课外活动进行调查,结果整理成下表,用你所学过的知识进行分析,能否有99.5%的把握认为“喜欢体育还是文娱与性别有关系”
体育 文娱 合计
男生 21 23 44
女生 6 29 35
合计 27 52 79
附:χ2=.
P(χ2≥x0) 0.05 0.025 0.010 0.005
x0 3.841 5.024 6.635 7.879
16.(15分)随着科技发展的日新月异,人工智能融入了各个行业,促进了社会的快速发展.其中利用人工智能生成的虚拟角色因为拥有更低的人工成本,正逐步取代传统的真人直播带货.某公司使用虚拟角色直播带货销售金额得到逐步提升,以下为该公司自2023年8月使用虚拟角色直播带货后的销售金额情况统计.
年月 2023年 8月 2023年 9月 2023年 10月 2023年 11月 2023年 12月 2024年 1月
月份编号x 1 2 3 4 5 6
销售金额 y/万元 15.4 25.4 35.4 85.4 155.4 195.4
若y与x的相关关系拟用线性回归模型表示,回答如下问题:
(1)试求变量y与x的相关系数r(结果精确到0.01);
(2)试求y关于x的线性回归方程,并据此预测2024年2月份该公司的销售金额.(均保留一位小数)
参考数据:xiyi=2 463.4,=20.
.
17.(15分)数独是源自18世纪瑞士的一种数学游戏,玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(3×3)内的数字均含1~9,且不重复.数独爱好者小明打算报名参加“丝路杯”全国数独大赛初级组的比赛.
(1)赛前小明进行了一段时间的训练,每天解题的平均速度y(秒/题)与训练天数x(天)有关,经统计得到如下数据:
x(天) 1 2 3 4 5 6 7
y(秒/题) 910 800 600 440 300 240 210
现用=+作为回归方程模型,请利用表中数据,求出该回归方程;(用分数表示)
(2)小明和小红玩“对战赛”,每局两人同时开始解一道数独题,先解出题的人获胜,不存在平局,两人约定先胜3局者赢得比赛.若小明每局获胜的概率为,且各局之间相互独立,设比赛X局后结束,求随机变量X的分布列及均值.
参考数据:
tiyi t-72
1 750 0.37 0.55
参考公式:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其线性回归方程=+μ的斜率和截距的最小二乘估计分别为= ,=-.
18.(17分)我国风云系列卫星可以监测气象和国土资源情况.某地区水文研究人员为了了解汛期人工测雨量x(单位:dm)与遥测雨量y(单位:dm)的关系,统计得到该地区10组雨量数据如表:
样本号i 1 2 3 4 5 6 7 8 9 10
人工测 雨量xi 5.38 7.99 6.37 6.71 7.53 5.53 4.18 4.04 6.02 4.23
遥测雨 量yi 5.43 8.07 6.57 6.14 7.95 5.56 4.27 4.15 6.04 4.49
|xi-yi| 0.05 0.08 0.2 0.57 0.42 0.03 0.09 0.11 0.02 0.26
并计算得≈353.6,≈361.7,xiyi≈357.3,≈33.62,≈34.42, ≈34.02.
(1)求该地区汛期遥测雨量y与人工测雨量x的相关系数(精确到0.01),并判断它们是否具有线性相关关系;
(2)规定:数组(xi,yi)满足|xi-yi|<0.1为“Ⅰ类误差”;满足0.1≤|xi-yi|<0.3为“Ⅱ类误差”;满足|xi-yi|≥0.3为“Ⅲ类误差”.为进一步研究,该地区水文研究人员从“Ⅰ类误差”“Ⅱ类误差”中随机抽取3组数据与“Ⅲ类误差”数据进行对比,记抽到“Ⅰ类误差”的数据的组数为X,求X的概率分布与数学期望.
附:相关系数r=,≈17.4.
19.(17分)为考察药物M对预防疾病A以及药物N对治疗疾病A的效果,科研团队进行了大量动物对照试验.根据100个简单随机样本的数据,得到如下列联表:(单位:只)
药物M 疾病A 合计
未患病 患病
未服用 30 15 45
服用 45 10 55
合计 75 25 100
(1)根据表中所给数据,判断能否有99%的把握认为药物M对预防疾病A有效果;
(2)用频率估计概率,现从患病的动物中用随机抽样的方法每次选取1只,用药物N进行治疗.已知药物N的治愈率如下:对未服用过药物M的动物治愈率为,对服用过药物M的动物治愈率为.若共选取3次,每次选取的结果是相互独立的.记选取的3只动物中被治愈的动物个数为X,求X的分布列和数学期望.
阶段质量评价(四)
1.选A 人所站的高度越高则视野越开阔,具有正相关关系,故A正确;人眼的近视程度与身高不具有相关关系,故B错误;正方体的体积与棱长是一种确定关系,故C错误;某同学的学籍号与考试成绩不具有相关关系,故D错误.故选A.
2.选D 由相关系数r1=-0.734<0,可知变量X与Y之间呈负线性相关关系,由相关系数r2=0.984>0,可知变量U与V之间呈正线性相关关系,又|r1|<|r2|,所以变量U与V的线性相关程度比变量X与Y的线性相关程度强.故选D.
3.选C Y随X的增大而增大,故变量Y与X正相关,即r1>0;V随U的增大而减小,故变量V与U负相关,即r2<0,故r2<0
5.选A 因为所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+1上,所以它们负相关,相关系数为-1.故选A.
6.选C 对于A,两个变量为函数关系,不是线性相关关系,故A错误;对于B,所有点不是在一条直线附近波动,不是线性相关关系,故B错误;对于C,对于两个变量x,y,y随着x的增加而减少,且所有点都在一条直线附近波动,所以具有线性相关关系,故C正确;对于D,两个变量不具有相关性,故D错误.故选C.
7.选BC 设男生的人数为6n(n∈N*),
根据题意列出2×2列联表如下表所示:
男生 女生 合计
喜欢 5n 4n 9n
不喜欢 n 2n 3n
合计 6n 6n 12n
则χ2==,
由于有95%的把握认为是否喜欢和性别有关,则3.841<χ2≤6.635,即3.841<≤6.635,得8.642 3
8.选C 由条件可知=1,=ln yi=10,代入=bx+6 b=4,则z=ln y=ln a+kx=4x+6 k=4,a=e6,故C正确.故选C.
9.选ABC 根据题意可得,=4,==5,所以样本中心点为(4,5).将样本中心点(4,5)代入线性回归方程y=1.23x+中,可得=0.08,故A正确;由表中数据可得y随着x增大而增大,x与y正相关,所以相关系数r>0,故B正确;维修费用从小到大依次为2.2,3.8,5.5,6.5,7,60百分位数为=6,故C正确;根据回归分析的概念,机床投入生产的时间为 10年时,所需要支出的维修费用大概是12.38万元,故D错误.故选ABC.
10.选AD 因为在校学生中有400名男生,500名女生,随机调查了40名男生和50名女生,男女比例始终是4∶5,所以采用了分层抽样的方法,故A正确;调查的90人中,对学校课后延时服务满意的人数为90×=60,其中男生满意的人数为40-10=30,所以女生满意的人数为30,女生不满意的人数为20,故B错误;由B选项的分析,补全列联表如下:
满意 不满意 合计
男 30 10 40
女 30 20 50
合计 60 30 90
由列联表可得χ2==,故C错误;提出假设H0:对课后延时服务的满意度与性别无关,由χ2=<10.828,没有充足的证据推断H0不成立,即不能认为“对课后延时服务的满意度与性别有关系”,故D正确.故选AD.
11.选BC 由于10,11,11,12,13,14,16,18,20,22共10个数据,且10×0.4=4,故40百分位数为第4,5个数据的平均数=12.5,故A错误;设数据x1,x2,…,x10的平均数为=,方差为s2=[++…+],则数据2x1+1,2x2+1,…,2x10+1的平均数为
'=
==2+1,
方差为=[++…+]=[++…+]=[++…+]=4s2=8,所以s2=2,故B正确;P(X≥-2)+P(X≥6)=1则P(X≥6)=1-P(X≥-2)=P(X≤-2),即P(X≥6)=P(X≤-2),由正态分布N(μ,σ2)的性质可得μ==2,故C正确;在独立性检验中,提出假设H0:分类变量X和Y独立.当χ2≥x0时,我们就推断H0不成立,即认为X和Y不独立;当χ2
答案:乙
13.解析:由题设,令z=ln =-a,则==,==,所以=-a a=-4,则z=ln =+4,所以x=8代入回归方程,则z=ln =5.6,可得=e5.6万元.
答案:e5.6
14.解析:补全2×2列联表:
y1 y2 合计
x1 49 21 70
x2 5 25 30
合计 54 46 100
所以b-d=54-46=8,χ2=≈24.047.
答案:8 24.047
15.解:提出假设
H0:喜欢体育还是文娱与性别没有关系.
因为a=21,b=23,c=6,d=29,n=79,
则χ2===8.106>7.879,
因为当H0成立时,χ2≥7.879的概率约为0.005,
所以我们有99.5%的把握认为喜欢体育还是文娱与性别有关系.
16.解: (1)==3.5,
==85.4,
-6=1+4+9+16+25+36-6×12.25=17.5,
所以r=
==≈0.96.
(2)由题意=
=≈38.3,
所以=85.4-38.3×3.5≈-48.7,
所以y关于x的线性回归方程为y=38.3x-48.7,
所以预测2024年2月份该公司的销售金额为y=38.3×7-48.7=219.4万元.
17.解: (1)因为=+,ti=,所以=+t.
因为==500,
所以====,
所以=-=500-×0.37=,
所以=+t,
所以所求回归方程为=+.
(2)随机变量X的所有可能取值为3,4,5,
则P(X=3)=+=,
P(X=4)=××+××=,
P(X=5)=××+××=.
所以随机变量X的概率分布为
X 3 4 5
P
E(X)=3×+4×+5×=.
18.解: (1)因为r=
=
≈=≈0.98,
所以该地区汛期遥测雨量与人工测雨量有很强的线性相关关系.
(2)依题意,“Ⅰ类误差”有5组,“Ⅱ类误差”有3组,“Ⅲ类误差”有2组.
若从“Ⅰ类误差”和“Ⅱ类误差”数据中抽取3组,抽到“Ⅰ类误差”的组数X的所有可能取值为0,1,2,3,
则P(X=0)==,P(X=1)==,
P(X=2)===,
P(X=3)===,
所以X的概率分布为
X 0 1 2 3
P
法一 E(X)=0×+1×+2×+3×=.
法二 因为X~H(3,5,8),所以E(X)==.
19.解:(1)提出假设
H0:药物M对预防疾病A无效果,
根据列联表中的数据,经计算得到
χ2==≈3.030>2.706,
因为当H0成立时,P(χ2≥2.706)≈0.1,所以有99%的把握认为药物M对预防疾病A有效果.
(2)设A表示药物N的治愈率,B1表示未服用过药物M,B2表示服用过药物M,
由题意可得P(B1)==0.6,P(B2)==0.4,且P(A|B1)=0.5,P(A|B2)=0.75,
P(A)=P(B1)×P(A|B1)+P(B2)×P(A|B2)=0.6×0.5+0.4×0.75=0.6,
所以药物N的治愈率P=0.6=,
则X~B,
所以P(X=0)==,
P(X=1)==,
P(X=2)==,P(X=3)==,
所以随机变量X的概率分布如下表所示:
X 0 1 2 3
P
E(X)=0×+1×+2×+3×=.
1 / 8
