人教A版高中数学选择性必修第一册1.4.1空间中直线、平面的垂直(第3课时) 课件(共68张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.4.1空间中直线、平面的垂直(第3课时) 课件(共68张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 00:00:00 | ||
图片预览









文档简介
(共68张PPT)
1.4.1 用空间向量研究直线、
平面的位置关系
第三课时 空间中直线、平面的垂直
人教A版2019高二数学(选修一)第一章 空间向量与立体几何
学习目标
1.用向量语言描述线线、线面、面面垂直的关系(重点)
2.用向量语言证明直线、平面垂直的相关判定定理(重点)
3.用向量语言解决立体几何直线、平面垂直的相关问题(难点)
类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系?观察下图回答。
位置关系 向量表示
线线垂直 设直线l1,l2的方向向量分别为u1,u2,则l1⊥l2 u1⊥u2 u1·u2=0
线面垂直 设直线l的方向向量为u,平面α的法向量为n,则l⊥α u∥n λ∈R,使得u=λn
面面垂直 设平面α,β的法向量分别为n1,n2,则α⊥β n1⊥n2 n1·n2=0
情景导入
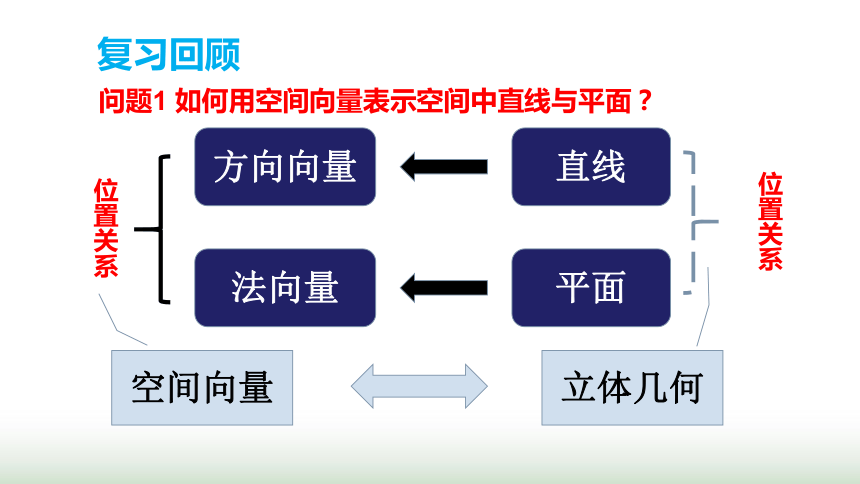
直线
平面
方向向量
法向量
位置关系
空间向量
立体几何
位置关系
问题1 如何用空间向量表示空间中直线与平面?
复习回顾
线线平行
线面平行
面面平行
类似空间中直线、平面平行的向量表示,在直线与直线,直线与直线,平面与平面的垂直关系中,直线的方向向量与平面的法向量之间有什么关系?
1.空间中直线、平面垂直
新知探究
问题2 由直线与直线垂直的关系,可以得到这两条直线的方向向量有什么关系?
显然的,就是这两条直线的方向向量垂直
l1
l2
(1)
问题3 由直线与平面平行的关系,可以得到直线的方向向量与平面的法向量有什么关系?
问题4 由平面与平面平行的关系,可以得到这两个平面的法向量有什么关系?
要求:
(1)以小组形式进行讨论,类比上一节课直线、平面平行的向量表示,回答出上述的两个问题;
(2)将上述的两个问题,能够数形结合的方式进行解释说明。
直线与平面垂直,就是直线的方向向量与平面的法向量平行;
l
(2)
概念归纳
(3)
平面与平面垂直,就是两平面的法向量垂直
概念归纳
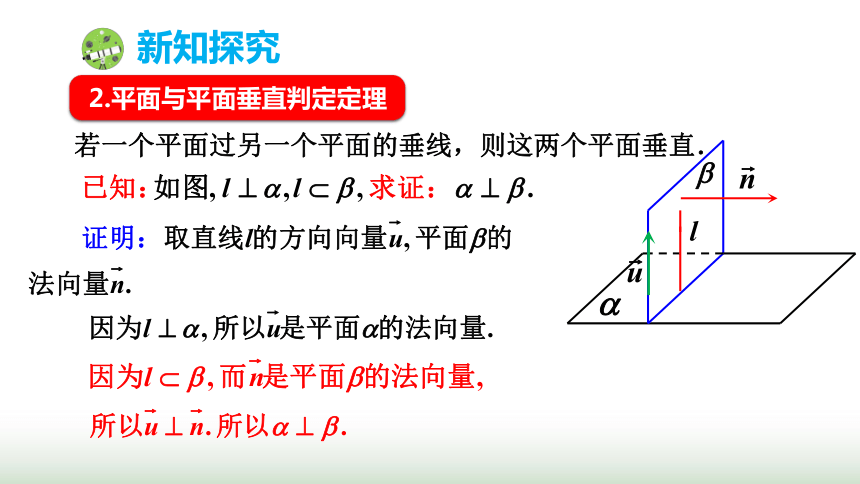
若一个平面过另一个平面的垂线,则这两个平面垂直.
l
2.平面与平面垂直判定定理
新知探究
1.数形结合
2.转化成数学符号
3.利用直线的方向向量与平面的法向量进行解答!
概念归纳
B
C
D
D1
A1
B1
C1
A
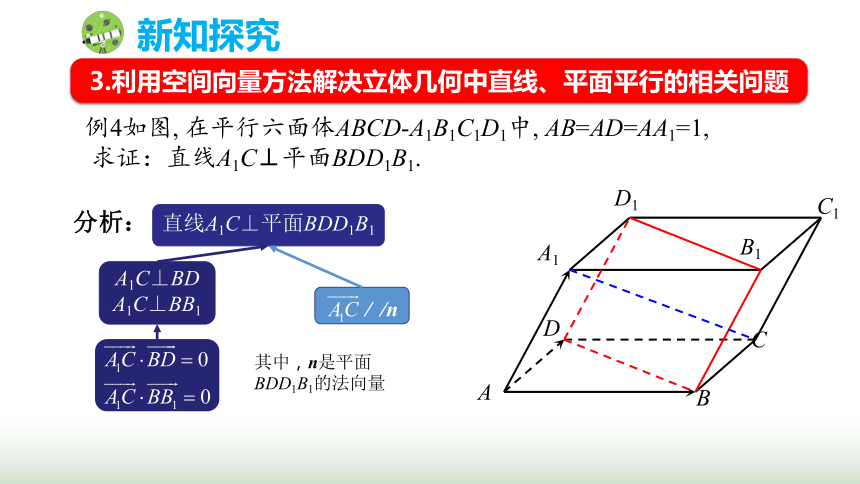
例4如图, 在平行六面体ABCD-A1B1C1D1中, AB=AD=AA1=1,
求证:直线A1C⊥平面BDD1B1.
分析:
直线A1C⊥平面BDD1B1
A1C⊥BD
A1C⊥BB1
其中,n是平面BDD1B1的法向量
3.利用空间向量方法解决立体几何中直线、平面平行的相关问题
新知探究
B
C
D
D1
A1
B1
C1
A
例4如图, 在平行六面体ABCD-A1B1C1D1中, AB=AD=AA1=1,
求证:直线A1C⊥平面BDD1B1.
证明:因为AB= AD =AA1=1,
所以
基底法
B
C
D
D1
A1
B1
C1
A
证明:
则对于平面BDD1B1上任意一点P,
存在唯一的有序实数对 ,
使得 .
在平面BDD1B1上, 取 为基向量,
基底法
l
例5 证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
如图,PA⊥平面ABCD,四边形ABCD为正方形,E是CD的中点,F是AD上一点,当BF⊥PE时,AF∶FD的值为 ( )
A.1∶2 B.1∶1
C.3∶1 D.2∶1
素养点睛:考查直观想象、数学运算的核心素养.
题型1 线线垂直问题
B
典例剖析
1.利用向量法证明线线垂直的依据和关键点
(1)依据:转化为证明直线的方向向量垂直,即证明它们的方向向量的数量积为0.
(2)关键:建立恰当的空间直角坐标系,正确地表示出点的坐标,进而求直线的方向向量.
2.应用线线垂直求点的坐标的策略
(1)设出点的坐标.
(2)利用点满足的条件建立与坐标有关的方程.
(3)通过解方程的方法求出点的坐标.
概念归纳
1.如图,已知在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=BB1.求证:BC1⊥AB1.
练一练
证明:如图,以点C1为原点,分别以C1A1,C1B1,C1C所在直线为x轴、y轴、z轴建立空间直角坐标系.
练一练
如图,在正方体ABCD-A1B1C1D1中,M,N分别为AB,B1C中点.求证:MN⊥平面A1BD.
素养点睛:考查直观想象、数学运算的核心素养.
题型2 线面垂直问题
典例剖析
用坐标法证明线面垂直的方法及步骤
方法一:(1)建立空间直角坐标系.
(2)将直线的方向向量用坐标表示.
(3)找出平面内两条相交直线,并用坐标表示它们的方向向量.
(4)分别计算两组向量的数量积,得到数量积为0.
方法二:(1)建立空间直角坐标系.
(2)将直线的方向向量用坐标表示.
(3)求出平面的法向量.
(4)判断直线的方向向量与平面的法向量平行.
提醒:用坐标证明垂直问题,关键是根据题目中的垂直关系建立适当的坐标系.
概念归纳
练一练
证明:(1)建立如图所示的空间直角坐标系,则B(0,0,0),E(3,0,1),F(0,3,2),D1(3,3,3),
典例剖析
方向2 探究性问题
在正方体ABCD-A1B1C1D1中,E是棱BC的中点,试在棱CC1上求一点P,使得平面A1B1P⊥平面C1DE.
素养点睛:考查直观想象、数学运算的
核心素养.
典例剖析
解:建立如图所示的空间直角坐标系.
用坐标法证明线面垂直的方法及步骤
(1)建立空间直角坐标系.
(2)将一平面内两相交直线的方向向量用坐标表示.
(3)由两条相交直线的方向向量,计算两组向量的数量积,得到数量积为0.
(4)同理求出另一个平面的法向量.
概念归纳
探索性问题的解决方法
(1)猜测法:猜测满足的条件,然后以此为基础结合题目中的其他条件进行证明结论成立,或者利用题目条件用变量设出条件,再结合结论逆向推导出变量的取值.
(2)逆推法:利用结论探求条件;如果是存在型问题,那么先假设结论存在,若推证无矛盾,则结论存在;若推证出矛盾,则结论不存在.
概念归纳
3.在三棱锥P-ABC中,三条侧棱两两互相垂直且相等,G是△PAB的重心,E,F分别为BC,PB上的点,且BE∶EC=PF∶FB=1∶2.求证:平面EFG⊥平面PBC.
证明:方法一,如图,以三棱锥的顶点P为原点,以PA,PB,PC所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
令PA=PB=PC=3,则A(3,0,0),B(0,3,0),
C(0,0,3),E(0,2,1),F(0,1,0),G(1,1,0),P(0,0,0),
练一练
如图,在棱长为2的正方体中ABCD-A1B1C1D1,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2).
(1)当λ=1时,求证:直线BC1∥平面EFPQ.
(2)是否存在λ,使平面EFPQ与平面PQMN
所成的二面角为直二面角?若存在,求出λ
的值;若不存在,说明理由.
规范解答 利用空间向量解答平行、垂直问题
典例剖析
分析:(1)要证明BC1∥平面EFPQ,只要证明BC1与平面EFPQ内的一条直线平行,依据题意可证BC1∥FP.
(2)由平面EFPQ与平面PQMN所成的二面角为直二面角知,两个平面互相垂直,故它们的法向量互相垂直,由此可根据数量积为0,求λ的值.
反思感悟
1.关注解决空间平行、垂直关系的依据
平行、垂直关系的向量表示是解题依据,是解题的前提和根本,也是避免无谓丢分的关键,如本例利用向量平行证明线线平行;通过证明两个平面的法向量互相垂直,得两个平面互相垂直.
2.准确计算,避免失误
利用向量法解决空间平行垂直问题的最大特点是通过计算证明位置关系,这也是向量法与几何法的主要区别.因此,准确计算是此类问题的关键,如本例中两个平面的法向量坐标必须计算准确.
概念归纳
课本练习
A
B
C
D
D1
A1
B1
C1
x
y
z
A
B
C
D
D1
A1
B1
C1
E
F
x
y
z
A
B
C
D
D1
A1
B1
C1
E
F
x
y
z
1.若直线l1,l2的方向向量分别为a=(1,2,-2),b=(-2,3,2),则 ( )
A.l1∥l2 B.l1⊥l2
C.l1,l2相交不垂直 D.不能确定
【解析】因为a=(1,2,-2),b=(-2,3,2),所以1×(-2)+2×3+(-2)×2=0,即a·b=0,所以a⊥b.所以l1⊥l2.
分层练习-基础
B
2.两平面α,β的法向量分别为u=(3,-1,z),v=(-2,-y,1),若α⊥β,则y+z的值是 ( )
A.-3 B.6
C.-6 D.-12
【解析】α⊥β u·v=0 -6+y+z=0,即y+z=6.
分层练习-基础
B
4
分层练习-基础
4.向量a=(-1,2,-4),b=(2,-2,3)是平面α内的两个不共线的向量,直线l的一个方向向量m=(2,3,1),则l与α是否垂直?________(填“是”或“否”).
【答案】否
【解析】m·a=(2,3,1)·(-1,2,-4)=-2+6-4=0,m·b=(2,3,1)·(2,-2,3)=4-6+3=1≠0.所以l与α不垂直.
分层练习-基础
5.如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.求证:平面ADE⊥平面ABE.
分层练习-巩固
分层练习-巩固
分层练习-巩固
6.在正方体ABCD-A1B1C1D1中,E为AC的中点.求证:
(1)BD1⊥AC;
(2)BD1⊥EB1.
分层练习-巩固
证明 以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.设正方体的棱长为1,则
分层练习-巩固
7.如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,
AB=4,AD=2 ,CD=2,PA⊥平面ABCD,PA=4.求证:BD⊥平面PAC.
分层练习-巩固
证明 因为AP⊥平面ABCD,AB⊥AD,所以以A为坐标原点,AB,AD,AP所在的直线分别为x轴、y轴、z轴建立空间直角坐标系.
分层练习-巩固
8.如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE= AD.
求证:平面AMD⊥平面CDE.
分层练习-巩固
证明 如图,建立空间直角坐标系,点A为坐标原点,AB,AD,AF所在直线分别
因此CE⊥AM,CE⊥AD.
又AM∩AD=A,∴CE⊥平面AMD.
又CE 平面CED,
∴平面AMD⊥平面CED.
分层练习-巩固
如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,E是B1C的中点.
(2)在线段AA1上是否存在点F,使CF⊥平面B1DF 若存在,求出 ;若不存在,请说明理由.
分层练习-拓展
【规范答题】
解 (1)以B为坐标原点,BA,BC,BB1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系.
分层练习-拓展
分层练习-拓展
线线平行
线面平行
面面平行
线线垂直
线面垂直
面面垂直
课堂小结
1.4.1 用空间向量研究直线、
平面的位置关系
第三课时 空间中直线、平面的垂直
人教A版2019高二数学(选修一)第一章 空间向量与立体几何
学习目标
1.用向量语言描述线线、线面、面面垂直的关系(重点)
2.用向量语言证明直线、平面垂直的相关判定定理(重点)
3.用向量语言解决立体几何直线、平面垂直的相关问题(难点)
类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系?观察下图回答。
位置关系 向量表示
线线垂直 设直线l1,l2的方向向量分别为u1,u2,则l1⊥l2 u1⊥u2 u1·u2=0
线面垂直 设直线l的方向向量为u,平面α的法向量为n,则l⊥α u∥n λ∈R,使得u=λn
面面垂直 设平面α,β的法向量分别为n1,n2,则α⊥β n1⊥n2 n1·n2=0
情景导入
直线
平面
方向向量
法向量
位置关系
空间向量
立体几何
位置关系
问题1 如何用空间向量表示空间中直线与平面?
复习回顾
线线平行
线面平行
面面平行
类似空间中直线、平面平行的向量表示,在直线与直线,直线与直线,平面与平面的垂直关系中,直线的方向向量与平面的法向量之间有什么关系?
1.空间中直线、平面垂直
新知探究
问题2 由直线与直线垂直的关系,可以得到这两条直线的方向向量有什么关系?
显然的,就是这两条直线的方向向量垂直
l1
l2
(1)
问题3 由直线与平面平行的关系,可以得到直线的方向向量与平面的法向量有什么关系?
问题4 由平面与平面平行的关系,可以得到这两个平面的法向量有什么关系?
要求:
(1)以小组形式进行讨论,类比上一节课直线、平面平行的向量表示,回答出上述的两个问题;
(2)将上述的两个问题,能够数形结合的方式进行解释说明。
直线与平面垂直,就是直线的方向向量与平面的法向量平行;
l
(2)
概念归纳
(3)
平面与平面垂直,就是两平面的法向量垂直
概念归纳
若一个平面过另一个平面的垂线,则这两个平面垂直.
l
2.平面与平面垂直判定定理
新知探究
1.数形结合
2.转化成数学符号
3.利用直线的方向向量与平面的法向量进行解答!
概念归纳
B
C
D
D1
A1
B1
C1
A
例4如图, 在平行六面体ABCD-A1B1C1D1中, AB=AD=AA1=1,
求证:直线A1C⊥平面BDD1B1.
分析:
直线A1C⊥平面BDD1B1
A1C⊥BD
A1C⊥BB1
其中,n是平面BDD1B1的法向量
3.利用空间向量方法解决立体几何中直线、平面平行的相关问题
新知探究
B
C
D
D1
A1
B1
C1
A
例4如图, 在平行六面体ABCD-A1B1C1D1中, AB=AD=AA1=1,
求证:直线A1C⊥平面BDD1B1.
证明:因为AB= AD =AA1=1,
所以
基底法
B
C
D
D1
A1
B1
C1
A
证明:
则对于平面BDD1B1上任意一点P,
存在唯一的有序实数对 ,
使得 .
在平面BDD1B1上, 取 为基向量,
基底法
l
例5 证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
如图,PA⊥平面ABCD,四边形ABCD为正方形,E是CD的中点,F是AD上一点,当BF⊥PE时,AF∶FD的值为 ( )
A.1∶2 B.1∶1
C.3∶1 D.2∶1
素养点睛:考查直观想象、数学运算的核心素养.
题型1 线线垂直问题
B
典例剖析
1.利用向量法证明线线垂直的依据和关键点
(1)依据:转化为证明直线的方向向量垂直,即证明它们的方向向量的数量积为0.
(2)关键:建立恰当的空间直角坐标系,正确地表示出点的坐标,进而求直线的方向向量.
2.应用线线垂直求点的坐标的策略
(1)设出点的坐标.
(2)利用点满足的条件建立与坐标有关的方程.
(3)通过解方程的方法求出点的坐标.
概念归纳
1.如图,已知在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=BB1.求证:BC1⊥AB1.
练一练
证明:如图,以点C1为原点,分别以C1A1,C1B1,C1C所在直线为x轴、y轴、z轴建立空间直角坐标系.
练一练
如图,在正方体ABCD-A1B1C1D1中,M,N分别为AB,B1C中点.求证:MN⊥平面A1BD.
素养点睛:考查直观想象、数学运算的核心素养.
题型2 线面垂直问题
典例剖析
用坐标法证明线面垂直的方法及步骤
方法一:(1)建立空间直角坐标系.
(2)将直线的方向向量用坐标表示.
(3)找出平面内两条相交直线,并用坐标表示它们的方向向量.
(4)分别计算两组向量的数量积,得到数量积为0.
方法二:(1)建立空间直角坐标系.
(2)将直线的方向向量用坐标表示.
(3)求出平面的法向量.
(4)判断直线的方向向量与平面的法向量平行.
提醒:用坐标证明垂直问题,关键是根据题目中的垂直关系建立适当的坐标系.
概念归纳
练一练
证明:(1)建立如图所示的空间直角坐标系,则B(0,0,0),E(3,0,1),F(0,3,2),D1(3,3,3),
典例剖析
方向2 探究性问题
在正方体ABCD-A1B1C1D1中,E是棱BC的中点,试在棱CC1上求一点P,使得平面A1B1P⊥平面C1DE.
素养点睛:考查直观想象、数学运算的
核心素养.
典例剖析
解:建立如图所示的空间直角坐标系.
用坐标法证明线面垂直的方法及步骤
(1)建立空间直角坐标系.
(2)将一平面内两相交直线的方向向量用坐标表示.
(3)由两条相交直线的方向向量,计算两组向量的数量积,得到数量积为0.
(4)同理求出另一个平面的法向量.
概念归纳
探索性问题的解决方法
(1)猜测法:猜测满足的条件,然后以此为基础结合题目中的其他条件进行证明结论成立,或者利用题目条件用变量设出条件,再结合结论逆向推导出变量的取值.
(2)逆推法:利用结论探求条件;如果是存在型问题,那么先假设结论存在,若推证无矛盾,则结论存在;若推证出矛盾,则结论不存在.
概念归纳
3.在三棱锥P-ABC中,三条侧棱两两互相垂直且相等,G是△PAB的重心,E,F分别为BC,PB上的点,且BE∶EC=PF∶FB=1∶2.求证:平面EFG⊥平面PBC.
证明:方法一,如图,以三棱锥的顶点P为原点,以PA,PB,PC所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
令PA=PB=PC=3,则A(3,0,0),B(0,3,0),
C(0,0,3),E(0,2,1),F(0,1,0),G(1,1,0),P(0,0,0),
练一练
如图,在棱长为2的正方体中ABCD-A1B1C1D1,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2).
(1)当λ=1时,求证:直线BC1∥平面EFPQ.
(2)是否存在λ,使平面EFPQ与平面PQMN
所成的二面角为直二面角?若存在,求出λ
的值;若不存在,说明理由.
规范解答 利用空间向量解答平行、垂直问题
典例剖析
分析:(1)要证明BC1∥平面EFPQ,只要证明BC1与平面EFPQ内的一条直线平行,依据题意可证BC1∥FP.
(2)由平面EFPQ与平面PQMN所成的二面角为直二面角知,两个平面互相垂直,故它们的法向量互相垂直,由此可根据数量积为0,求λ的值.
反思感悟
1.关注解决空间平行、垂直关系的依据
平行、垂直关系的向量表示是解题依据,是解题的前提和根本,也是避免无谓丢分的关键,如本例利用向量平行证明线线平行;通过证明两个平面的法向量互相垂直,得两个平面互相垂直.
2.准确计算,避免失误
利用向量法解决空间平行垂直问题的最大特点是通过计算证明位置关系,这也是向量法与几何法的主要区别.因此,准确计算是此类问题的关键,如本例中两个平面的法向量坐标必须计算准确.
概念归纳
课本练习
A
B
C
D
D1
A1
B1
C1
x
y
z
A
B
C
D
D1
A1
B1
C1
E
F
x
y
z
A
B
C
D
D1
A1
B1
C1
E
F
x
y
z
1.若直线l1,l2的方向向量分别为a=(1,2,-2),b=(-2,3,2),则 ( )
A.l1∥l2 B.l1⊥l2
C.l1,l2相交不垂直 D.不能确定
【解析】因为a=(1,2,-2),b=(-2,3,2),所以1×(-2)+2×3+(-2)×2=0,即a·b=0,所以a⊥b.所以l1⊥l2.
分层练习-基础
B
2.两平面α,β的法向量分别为u=(3,-1,z),v=(-2,-y,1),若α⊥β,则y+z的值是 ( )
A.-3 B.6
C.-6 D.-12
【解析】α⊥β u·v=0 -6+y+z=0,即y+z=6.
分层练习-基础
B
4
分层练习-基础
4.向量a=(-1,2,-4),b=(2,-2,3)是平面α内的两个不共线的向量,直线l的一个方向向量m=(2,3,1),则l与α是否垂直?________(填“是”或“否”).
【答案】否
【解析】m·a=(2,3,1)·(-1,2,-4)=-2+6-4=0,m·b=(2,3,1)·(2,-2,3)=4-6+3=1≠0.所以l与α不垂直.
分层练习-基础
5.如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.求证:平面ADE⊥平面ABE.
分层练习-巩固
分层练习-巩固
分层练习-巩固
6.在正方体ABCD-A1B1C1D1中,E为AC的中点.求证:
(1)BD1⊥AC;
(2)BD1⊥EB1.
分层练习-巩固
证明 以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.设正方体的棱长为1,则
分层练习-巩固
7.如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,
AB=4,AD=2 ,CD=2,PA⊥平面ABCD,PA=4.求证:BD⊥平面PAC.
分层练习-巩固
证明 因为AP⊥平面ABCD,AB⊥AD,所以以A为坐标原点,AB,AD,AP所在的直线分别为x轴、y轴、z轴建立空间直角坐标系.
分层练习-巩固
8.如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE= AD.
求证:平面AMD⊥平面CDE.
分层练习-巩固
证明 如图,建立空间直角坐标系,点A为坐标原点,AB,AD,AF所在直线分别
因此CE⊥AM,CE⊥AD.
又AM∩AD=A,∴CE⊥平面AMD.
又CE 平面CED,
∴平面AMD⊥平面CED.
分层练习-巩固
如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,E是B1C的中点.
(2)在线段AA1上是否存在点F,使CF⊥平面B1DF 若存在,求出 ;若不存在,请说明理由.
分层练习-拓展
【规范答题】
解 (1)以B为坐标原点,BA,BC,BB1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系.
分层练习-拓展
分层练习-拓展
线线平行
线面平行
面面平行
线线垂直
线面垂直
面面垂直
课堂小结
