人教A版高中数学选择性必修第一册1.4.2用空间夹角研究夹角问题(第2课时) 课件(共101张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.4.2用空间夹角研究夹角问题(第2课时) 课件(共101张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 10:35:46 | ||
图片预览








文档简介
(共101张PPT)
人教A版2019高二数学(选修一)第一章 空间向量与立体几何
第二课时 用空间向量研究夹角问题
1.4.2 用空间向量研究距离、
夹角问题
学习目标
1.会用向量法解决线线角、线面角、面面角(重点)
2.会区分向量角与线线角、线面角、面面角的关系(难点)
3.能用向量夹角公式解决立体几何中角度的度量问题(难点)
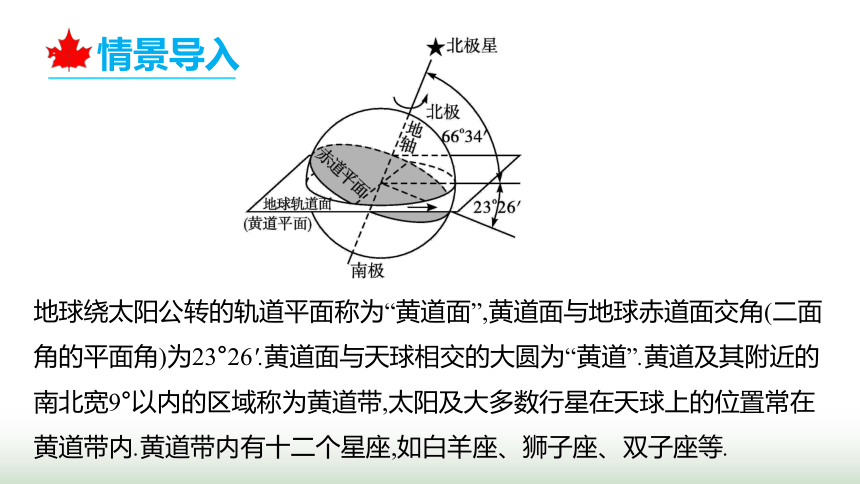
情景导入
地球绕太阳公转的轨道平面称为“黄道面”,黄道面与地球赤道面交角(二面角的平面角)为23°26'.黄道面与天球相交的大圆为“黄道”.黄道及其附近的南北宽9°以内的区域称为黄道带,太阳及大多数行星在天球上的位置常在黄道带内.黄道带内有十二个星座,如白羊座、狮子座、双子座等.
1.空间两点之间的距离
2. 点到直线的距离
两条平行直线的距离
复习回顾
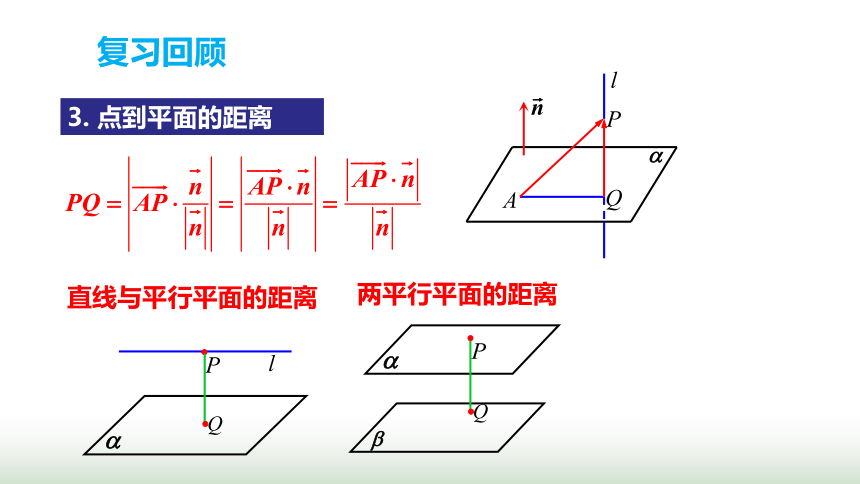
3. 点到平面的距离
A
P
Q
l
l
直线与平行平面的距离
两平行平面的距离
复习回顾
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何向题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
用空间向量解决立体几何问题的“三步曲”:
(化为向量问题)
(进行向量运算)
(回到图形)
复习回顾
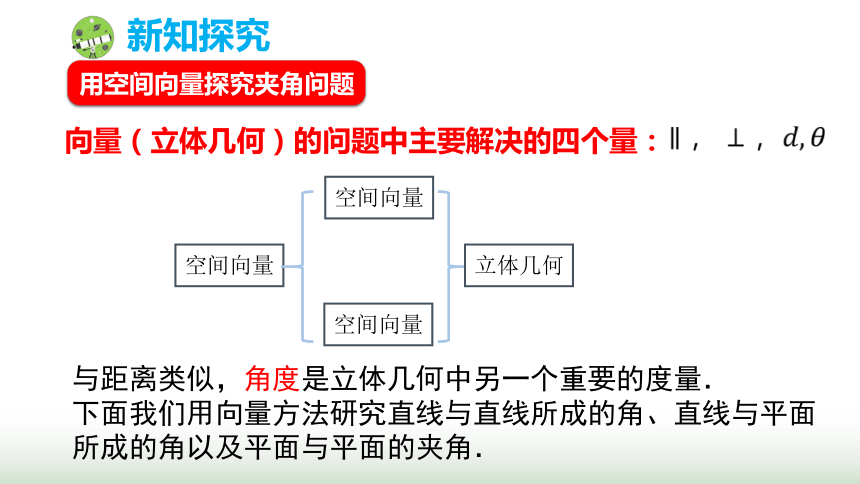
向量(立体几何)的问题中主要解决的四个量:
与距离类似,角度是立体几何中另一个重要的度量.
下面我们用向量方法研究直线与直线所成的角、直线与平面所成的角以及平面与平面的夹角.
用空间向量探究夹角问题
新知探究
空间向量
空间向量
空间向量
立体几何
问题1 向量的夹角有哪些公式可以用?
探究一:立体几何中线线角问题!
新知探究
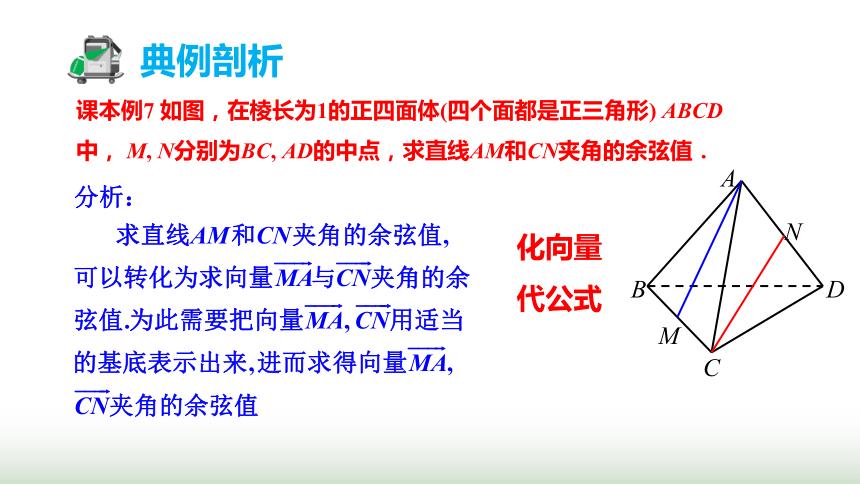
课本例7 如图,在棱长为1的正四面体(四个面都是正三角形) ABCD 中, M, N分别为BC, AD的中点,求直线AM和CN夹角的余弦值.
C
A
B
D
M
N
化向量
代公式
典例剖析
化为向量问题
进行向量运算
回到图形问题
代公式
概念归纳
概念归纳
1.利用空间向量求两异面直线所成角的步骤.
(1)建立适当的空间直角坐标系.
(2)求出两条异面直线的方向向量的坐标.
(3)利用向量的夹角公式求出两直线方向向量的夹角.
(4)结合异面直线所成角的范围得到两异面直线所成角.
2.求两条异面直线所成的角的两个关注点.
(1)余弦值非负:两条异面直线所成角的余弦值一定为非负值,而对应的方向向量的夹角可能为钝角.
(2)范围:异面直线所成角的范围是,故两直线方向向量夹角的余弦值为负时,应取其绝对值.
问题2 我们在例1用向量方法解决了异面直线AM和CN所成角的问题,你能用向量方法求直线AB与平面BCD所成的角吗?
法向量
再利用向量与向量的公式
探究二:立体几何中线面角问题
新知探究
A
B
C
课本例7(变式练)如图,在棱长为1的正四面体(四个面都是正三角形) ABCD 中, M, N分别为BC, AD的中点,求直线AB与平面BCD所成的角.
C
A
B
D
M
N
取向量(基底法)
求法向量
代公式
练一练
若直线l与平面α的夹角为θ,利用法向量计算θ的步骤如下:
基底
建系
确定向量
依据几何条件建立适当的坐标系
找直线的一个方向向量a
找平面的一个法向量n
概念归纳
问题3 图中有几个二面角?两个平面的夹角与这两个平面形成的二面角有什么关系?
探究三:立体几何中面面角(二面角)问题
新知探究
二面角的大小判断:肉眼观察法
概念归纳
A
B
C
C1
A1
B1
x
y
z
P
Q
R
大家小组可以探究一下:
(1)解答出结果
(2)总结步骤
典例剖析
化为向量问题:建系
进行向量运算
分别算法向量
套公式
回归图像
概念归纳
利用平面的法向量求两个平面的夹角
利用向量方法求两平面夹角大小时,多采用法向量法.即求出两个面的法向量,然后通过法向量的夹角来得到两平面夹角.需注意法向量夹角范围是[0,π],而两平面夹角范围是.
如图,在四面体ABCD中,AB⊥BC,AB⊥BD,BC⊥CD且AB=BC=6,BD=8,E为AD中点,求异面直线BE与CD所成角的余弦值.
素养点睛:考查直观想象、数学运算的核心素养.
题型1 异面直线所成的角
典例剖析
求异面直线所成的角主要方法有两种:一是向量法,根据几何体的特殊性质建立空间直角坐标系后,分别求出两直线的方向向量,再利用空间向量夹角的余弦公式求解;二是传统法,利用平行四边形、三角形中位线等方法找出两直线成的角,再利用平面几何性质求解.
概念归纳
1.如图,在正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点,求异面直线AE与D1F所成角.
练一练
解:如图,设正方体的棱长为1,建立空间直角坐标系Dxyz.
练一练
(1)证明:∵在△PAD中,由E,F为PD,PA中点得EF为中位线,∴EF∥AD.
又∵底面为矩形,AD∥BC,∴EF∥BC.
∴由平行线确定唯一平面得E,F,B,C在同一平面上.
(2)解:如图,以A为原点建立坐标系,其中AB,AD,AP分别为x轴、y轴、z轴,
如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,AD∥BC,∠ABC=90°,∠APB=90°.
(1)求证:AP⊥PC;
(2)设AB=5,AP=BC=2AD=4,求直线CB与平面PCD所成角的正弦值.
素养点睛:考查直观想象、数学运算的核心素养.
题型2 直线与平面所成的角
典例剖析
(1)证明:因为平面PAB⊥底面ABCD,∠ABC=90°,所以BC⊥平面PAB,则BC⊥AP.
又因为AP⊥PB,且PB∩BC=B,
故AP⊥平面PBC,所以AP⊥PC.
(2)解:如图,作PM⊥AB于点M,
则建立空间直角坐标系Mxyz,
概念归纳
练一练
典例剖析
素养点睛:考查直观想象、数学运算的核心素养.
典例剖析
素养点睛:考查直观想象、数学运算的核心素养.
图1
图2
利用坐标法求二面角的步骤
设n1,n2分别是平面α,β的法向量,则向量n1与n2的夹角(或其补角)就是两个平面夹角的大小,如图.
概念归纳
概念归纳
练一练
(1)证明:如图1,连接AC交BD于点O,
因为四边形ABCD为平行四边形,且AD=CD,
所以四边形ABCD为菱形,所以AC⊥BD.
因为BD∥平面AEQF,平面AEQF∩平面SBD=EF,BD 平面SBD,
所以BD∥EF.
因为BD⊥AC,
所以EF⊥AC.
图1
图 2
规范解答 利用向量法求空间角
典例剖析
审题指导:
(1)要证明DE⊥平面ACD,需要证明DE与平面ACD内两条相交直线垂直,其中DE⊥DC较明显,由平面ABC⊥平面BCDE,且AC⊥BC,证得AC⊥平面BCDE,从而DE⊥AC.
(2)要求二面角B-AD-E的大小,可先以D为原点建系,再求出平面ADE和平面ABD的法向量,最后由公式计算二面角的大小.
【点拨】
1.利用条件建立空间直角坐标系
充分利用题干中的垂直关系建立空间直角坐标系,使几何体的顶点尽量多地落在坐标轴上,建系或在求点的坐标时用到的位置关系和数量关系要进行必要的说明,如本例中,AC⊥平面BCDE,不仅用于证明AC⊥DE,还为求点A的坐标提供依据.
概念归纳
概念归纳
随堂练
随堂练
随堂练
A
B
C
C1
B1
A1
F1
D1
x
y
z
A
课本练习
A
B
C
C1
B1
A1
F1
D1
H
P
B
O
A
C
x
y
z
C
P
B
O
A
C
x
y
z
A
A1
B1
C1
C
B
x
y
z
O
H
A
B
C
D
x
y
z
A
B
C
D
x
y
z
(2)直线AD与平面BCD所成角的大小;
A
B
C
D
x
y
z
(3)平面ABD和平面BDC的夹角的余弦值.
1.若直线l的方向向量与平面α的法向量的夹角等于120°,则直线l与平面α所成的角等于 ( )
A.120° B.60°
C.30° D.以上均错
【答案】C
【解析】由直线与平面所成的角的范围及与向量所成角的关系知直线l与平面α所成的角等于90°-(180°-120°)=30°.
分层练习-基础
分层练习-基础
分层练习-基础
3.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角的大小为 ( )
A.45° B.135°
C.90° D.45°或135°
【答案】D
分层练习-基础
4.正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1C1的中点,则异面直线AE与CF所成角的余弦值为________.
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分析
分层练习-巩固
分层练习-拓展
分层练习-拓展
三步曲
角度
距离
证明
点到线距离
点到面距离
转化为点到线或点到面距离
实际问题
异面直线所成角
直线与平面所成角
两平面的夹角
平行
垂直
课堂小结
实质:线面距
人教A版2019高二数学(选修一)第一章 空间向量与立体几何
第二课时 用空间向量研究夹角问题
1.4.2 用空间向量研究距离、
夹角问题
学习目标
1.会用向量法解决线线角、线面角、面面角(重点)
2.会区分向量角与线线角、线面角、面面角的关系(难点)
3.能用向量夹角公式解决立体几何中角度的度量问题(难点)
情景导入
地球绕太阳公转的轨道平面称为“黄道面”,黄道面与地球赤道面交角(二面角的平面角)为23°26'.黄道面与天球相交的大圆为“黄道”.黄道及其附近的南北宽9°以内的区域称为黄道带,太阳及大多数行星在天球上的位置常在黄道带内.黄道带内有十二个星座,如白羊座、狮子座、双子座等.
1.空间两点之间的距离
2. 点到直线的距离
两条平行直线的距离
复习回顾
3. 点到平面的距离
A
P
Q
l
l
直线与平行平面的距离
两平行平面的距离
复习回顾
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何向题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
用空间向量解决立体几何问题的“三步曲”:
(化为向量问题)
(进行向量运算)
(回到图形)
复习回顾
向量(立体几何)的问题中主要解决的四个量:
与距离类似,角度是立体几何中另一个重要的度量.
下面我们用向量方法研究直线与直线所成的角、直线与平面所成的角以及平面与平面的夹角.
用空间向量探究夹角问题
新知探究
空间向量
空间向量
空间向量
立体几何
问题1 向量的夹角有哪些公式可以用?
探究一:立体几何中线线角问题!
新知探究
课本例7 如图,在棱长为1的正四面体(四个面都是正三角形) ABCD 中, M, N分别为BC, AD的中点,求直线AM和CN夹角的余弦值.
C
A
B
D
M
N
化向量
代公式
典例剖析
化为向量问题
进行向量运算
回到图形问题
代公式
概念归纳
概念归纳
1.利用空间向量求两异面直线所成角的步骤.
(1)建立适当的空间直角坐标系.
(2)求出两条异面直线的方向向量的坐标.
(3)利用向量的夹角公式求出两直线方向向量的夹角.
(4)结合异面直线所成角的范围得到两异面直线所成角.
2.求两条异面直线所成的角的两个关注点.
(1)余弦值非负:两条异面直线所成角的余弦值一定为非负值,而对应的方向向量的夹角可能为钝角.
(2)范围:异面直线所成角的范围是,故两直线方向向量夹角的余弦值为负时,应取其绝对值.
问题2 我们在例1用向量方法解决了异面直线AM和CN所成角的问题,你能用向量方法求直线AB与平面BCD所成的角吗?
法向量
再利用向量与向量的公式
探究二:立体几何中线面角问题
新知探究
A
B
C
课本例7(变式练)如图,在棱长为1的正四面体(四个面都是正三角形) ABCD 中, M, N分别为BC, AD的中点,求直线AB与平面BCD所成的角.
C
A
B
D
M
N
取向量(基底法)
求法向量
代公式
练一练
若直线l与平面α的夹角为θ,利用法向量计算θ的步骤如下:
基底
建系
确定向量
依据几何条件建立适当的坐标系
找直线的一个方向向量a
找平面的一个法向量n
概念归纳
问题3 图中有几个二面角?两个平面的夹角与这两个平面形成的二面角有什么关系?
探究三:立体几何中面面角(二面角)问题
新知探究
二面角的大小判断:肉眼观察法
概念归纳
A
B
C
C1
A1
B1
x
y
z
P
Q
R
大家小组可以探究一下:
(1)解答出结果
(2)总结步骤
典例剖析
化为向量问题:建系
进行向量运算
分别算法向量
套公式
回归图像
概念归纳
利用平面的法向量求两个平面的夹角
利用向量方法求两平面夹角大小时,多采用法向量法.即求出两个面的法向量,然后通过法向量的夹角来得到两平面夹角.需注意法向量夹角范围是[0,π],而两平面夹角范围是.
如图,在四面体ABCD中,AB⊥BC,AB⊥BD,BC⊥CD且AB=BC=6,BD=8,E为AD中点,求异面直线BE与CD所成角的余弦值.
素养点睛:考查直观想象、数学运算的核心素养.
题型1 异面直线所成的角
典例剖析
求异面直线所成的角主要方法有两种:一是向量法,根据几何体的特殊性质建立空间直角坐标系后,分别求出两直线的方向向量,再利用空间向量夹角的余弦公式求解;二是传统法,利用平行四边形、三角形中位线等方法找出两直线成的角,再利用平面几何性质求解.
概念归纳
1.如图,在正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点,求异面直线AE与D1F所成角.
练一练
解:如图,设正方体的棱长为1,建立空间直角坐标系Dxyz.
练一练
(1)证明:∵在△PAD中,由E,F为PD,PA中点得EF为中位线,∴EF∥AD.
又∵底面为矩形,AD∥BC,∴EF∥BC.
∴由平行线确定唯一平面得E,F,B,C在同一平面上.
(2)解:如图,以A为原点建立坐标系,其中AB,AD,AP分别为x轴、y轴、z轴,
如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,AD∥BC,∠ABC=90°,∠APB=90°.
(1)求证:AP⊥PC;
(2)设AB=5,AP=BC=2AD=4,求直线CB与平面PCD所成角的正弦值.
素养点睛:考查直观想象、数学运算的核心素养.
题型2 直线与平面所成的角
典例剖析
(1)证明:因为平面PAB⊥底面ABCD,∠ABC=90°,所以BC⊥平面PAB,则BC⊥AP.
又因为AP⊥PB,且PB∩BC=B,
故AP⊥平面PBC,所以AP⊥PC.
(2)解:如图,作PM⊥AB于点M,
则建立空间直角坐标系Mxyz,
概念归纳
练一练
典例剖析
素养点睛:考查直观想象、数学运算的核心素养.
典例剖析
素养点睛:考查直观想象、数学运算的核心素养.
图1
图2
利用坐标法求二面角的步骤
设n1,n2分别是平面α,β的法向量,则向量n1与n2的夹角(或其补角)就是两个平面夹角的大小,如图.
概念归纳
概念归纳
练一练
(1)证明:如图1,连接AC交BD于点O,
因为四边形ABCD为平行四边形,且AD=CD,
所以四边形ABCD为菱形,所以AC⊥BD.
因为BD∥平面AEQF,平面AEQF∩平面SBD=EF,BD 平面SBD,
所以BD∥EF.
因为BD⊥AC,
所以EF⊥AC.
图1
图 2
规范解答 利用向量法求空间角
典例剖析
审题指导:
(1)要证明DE⊥平面ACD,需要证明DE与平面ACD内两条相交直线垂直,其中DE⊥DC较明显,由平面ABC⊥平面BCDE,且AC⊥BC,证得AC⊥平面BCDE,从而DE⊥AC.
(2)要求二面角B-AD-E的大小,可先以D为原点建系,再求出平面ADE和平面ABD的法向量,最后由公式计算二面角的大小.
【点拨】
1.利用条件建立空间直角坐标系
充分利用题干中的垂直关系建立空间直角坐标系,使几何体的顶点尽量多地落在坐标轴上,建系或在求点的坐标时用到的位置关系和数量关系要进行必要的说明,如本例中,AC⊥平面BCDE,不仅用于证明AC⊥DE,还为求点A的坐标提供依据.
概念归纳
概念归纳
随堂练
随堂练
随堂练
A
B
C
C1
B1
A1
F1
D1
x
y
z
A
课本练习
A
B
C
C1
B1
A1
F1
D1
H
P
B
O
A
C
x
y
z
C
P
B
O
A
C
x
y
z
A
A1
B1
C1
C
B
x
y
z
O
H
A
B
C
D
x
y
z
A
B
C
D
x
y
z
(2)直线AD与平面BCD所成角的大小;
A
B
C
D
x
y
z
(3)平面ABD和平面BDC的夹角的余弦值.
1.若直线l的方向向量与平面α的法向量的夹角等于120°,则直线l与平面α所成的角等于 ( )
A.120° B.60°
C.30° D.以上均错
【答案】C
【解析】由直线与平面所成的角的范围及与向量所成角的关系知直线l与平面α所成的角等于90°-(180°-120°)=30°.
分层练习-基础
分层练习-基础
分层练习-基础
3.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角的大小为 ( )
A.45° B.135°
C.90° D.45°或135°
【答案】D
分层练习-基础
4.正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1C1的中点,则异面直线AE与CF所成角的余弦值为________.
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分析
分层练习-巩固
分层练习-拓展
分层练习-拓展
三步曲
角度
距离
证明
点到线距离
点到面距离
转化为点到线或点到面距离
实际问题
异面直线所成角
直线与平面所成角
两平面的夹角
平行
垂直
课堂小结
实质:线面距
