人教A版高中数学选择性必修第一册1.4.1空间中直线、平面的平行(第2课时) 课件(共48张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.4.1空间中直线、平面的平行(第2课时) 课件(共48张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 21:27:32 | ||
图片预览







文档简介
(共48张PPT)
1.4.1 用空间向量研究直线、
平面的位置关系
第二课时 空间中直线、平面的平行
人教A版2019高二数学(选修一)第一章 空间向量与立体几何
学习目标
能用向量语言描述直线和平面,理解直线的方向向量与平面的法向量.
会求直线的方向向量与平面的法向量.
能用向量语言表述直线与直线、直线与平面、平面与平面的平行关系.
能用向量方法判断或证明直线、平面间的平行关系.
能用向量方法证明必修内容中有关直线、平面位置关系的判断.
问题1:生活中有很多线线平行,线面平行,面面平行的建筑,比如左下图上海世博会的中国馆,右下图是加拿大馆,我们肯定不能仅凭眼睛判断建筑的各个面之间是否平行。
情景导入
下图是武汉大学校门,校门上部的下边线与柱子垂直,我们就能知道下边线与地面平行。这是为什么呢
问题1 如何求直线的方向向量与平面的法向量?
(1)建系
(2)算点
(3)取向量
(4)建方程组
(5)取解
(1)去两点
(2)算向量
(1)算点,设法
(2)取向量:面内两个不共线向量
(3)建方程组
(4)取解
复习回顾
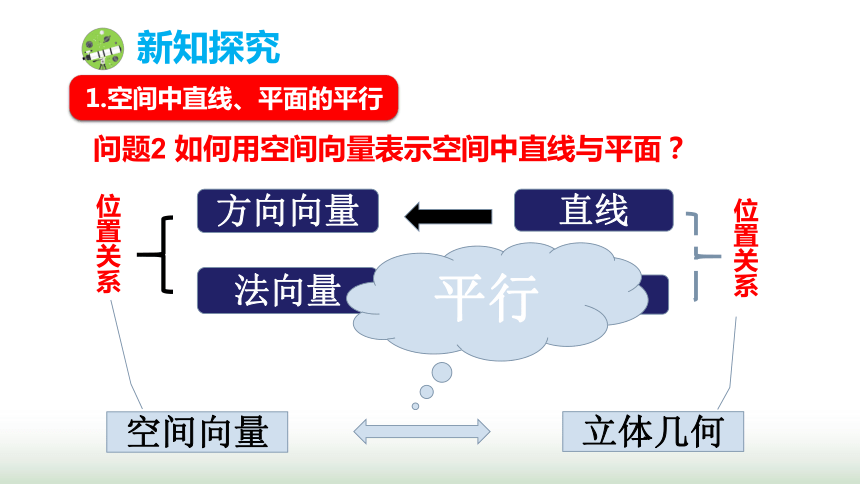
问题2 如何用空间向量表示空间中直线与平面?
直线
平面
方向向量
法向量
位置关系
位置关系
空间向量
立体几何
平行
1.空间中直线、平面的平行
新知探究
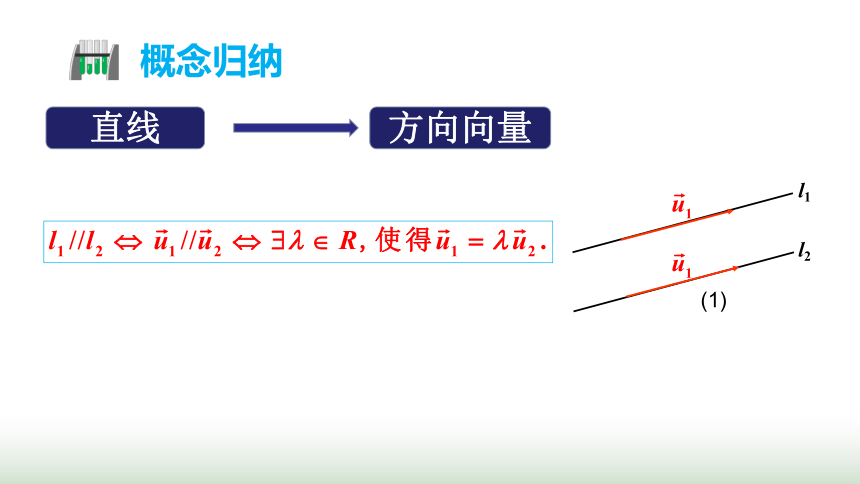
问题3 由直线与直线平行的关系,可以得到这两条直线的方向向量有什么关系?
l1
l2
(1)
l1
l2
(1)
直线
方向向量
概念归纳
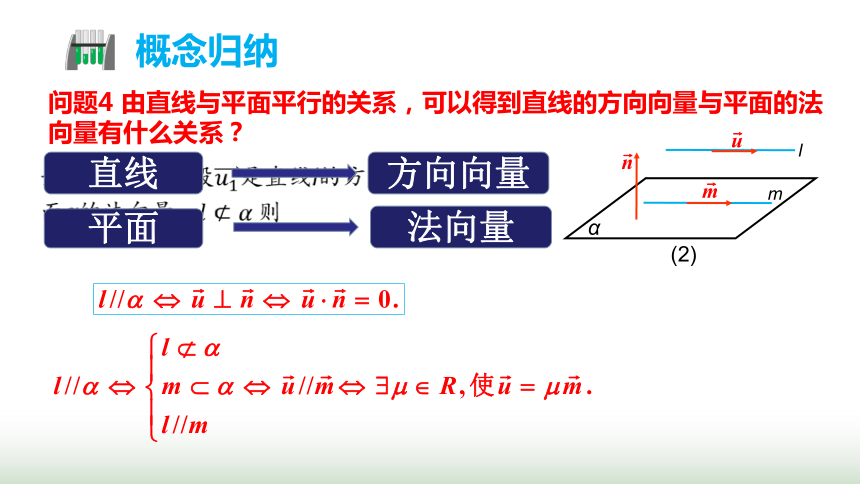
问题4 由直线与平面平行的关系,可以得到直线的方向向量与平面的法向量有什么关系?
α
l
(2)
m
直线
方向向量
平面
法向量
概念归纳
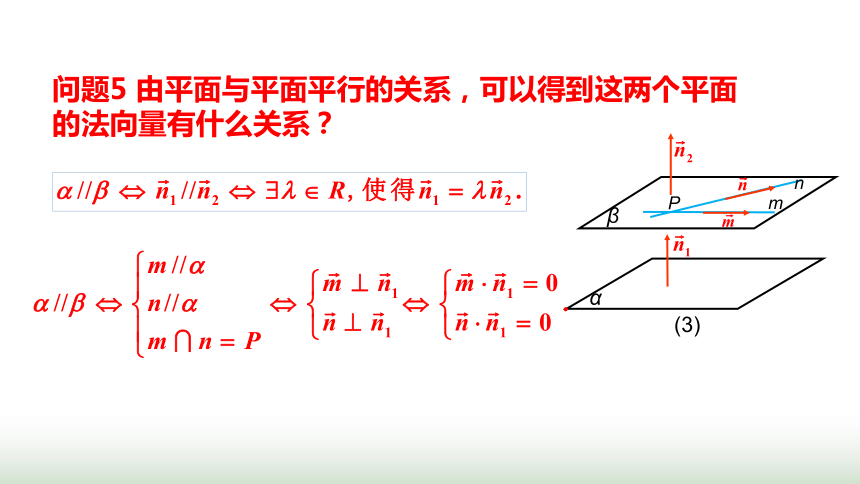
问题5 由平面与平面平行的关系,可以得到这两个平面的法向量有什么关系?
α
(3)
β
P
m
n
直线
方向向量
平面
法向量
转化
概念归纳
(1)证明“平面与平面平行的判定定理”
(2)证明“直线与平面平行的判定定理”
要求:
1.以小组形式进行讨论;
2.转化成数学语言,利用向量方法解释(数形结合)
3.总结方法
请你用向量的方法证明直线、平面平行相关的判定定理
2.直线、平面平行的判定定理
新知探究
(1)证明“平面与平面平行的判定定理”
α
β
P
b
a
换句话:两个平面的法向量共线
(2)证明“直线与平面平行的判定定理”
α
b
a
换句话:法向量与方向向量垂直
A
B
C
D
D1
A1
B1
C1
x
y
z
P
分析:
是否存在P?
找到P
如何判断
P在哪儿?
P在B1C上
如何表示
A1P//面ACD1
向量运算
确定存在
3.利用空间向量方法求解立体几何中直线、平面平行
新知探究
P30-例3.长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1=2,
线段B1C上是否存在点P,使得A1P∥平面ACD1.
x
y
z
坐标法
A
B
C
D
D1
A1
B1
C1
x
y
z
P
Q
方法二:立体几何先证再猜
作A1D的中点交AD1中于Q
建系
设点
取向量
通用
列方程组
取解
法向量
取两点
得向量
方向向量
运算
概念归纳
已知O为坐标原点,四面体OABC中,A,B,C的坐标分别为A(0,3,5),B(1,2,0),C(0,5,0),若直线AD∥BC且AD交坐标平面Ozx于点D,求点D的坐标.
素养点睛:考查直观想象、数学运算的核心素养.
题型1 空间中的线线平行问题
典例剖析
或0=-(x-1),2=-(y-2),-5=-z.
所以x=1,y=4,z=-5或x=1,y=0,z=5.
故D点坐标为(1,4,-5)或(1,0,5).
向量法处理空间平行问题的两个应用
(1)求字母的值:通过线线、线面、面面平行转化为向量的共线、垂直的关系,再利用向量关系构造关于字母的等量关系,进而求出字母的值.
(2)求点的坐标:可设出对应点的坐标,再利用点与向量的关系,写出对应向量,利用空间中点、线、面的位置关系,转化为向量的位置关系,进而建立与所求点的坐标有关的等式.
概念归纳
如图,在正方体ABCD-A1B1C1D1中,E,F分别为DD1和BB1的中点.求证:四边形AEC1F是平行四边形.
练一练
题型2 向量法证明线面、面面平行问题
(1)若平面α的一个法向量为u1=(-3,y,2),平面β的一个法向量为u2=(6,-2,z),且α∥β,则y+z=________.
(2)如图,在四棱锥S-ABCD中,底面ABCD为正
方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的
中点.求证:EF∥平面SAD.
素养点睛:考查直观想象、数学运算的核心素养.
典例剖析
【答案】(1)-3
1.用向量证明线面平行的方法
(1)证明该直线的方向向量与平面的某一法向量垂直.
(2)证明该直线的方向向量与平面内某直线的方向向量平行.
(3)证明该直线的方向向量可以用平面内的两个不共线的向量线性表示.
2.向量法证明面面平行的方法
设平面α的法向量为n1=(a1,b1,c1),平面β的法向量为n2=(a2,b2,c2),则α∥β n1∥n2 (a1,b1,c1)=k(a2,b2,c2)(k∈R).
概念归纳
练一练
1.用向量方法证明“直线与平面平行的判定定理”:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
l
m
课本练习
A
B
C
D
E
F
A
B
C
D
E
F
此方程组无解
A
B
C
D
D1
A1
B1
C1
F
E
x
y
z
A
B
C
D
D1
A1
B1
C1
F
E
x
y
z
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分析
分层练习-巩固
分层练习-拓展
分层练习-拓展
线线平行
线面平行
面面平行
课堂小结
其中, 分别是直线 的方向向量;
分别是平面 的法向量.
(一)建系;
(二)设点;
(三)表示相关向量;
(四)进行向量运算;
(五)把向量运算的结果”翻译”为几何结论.
数学运算
直观想象
逻辑推理
解决几何问题的步骤.
1.4.1 用空间向量研究直线、
平面的位置关系
第二课时 空间中直线、平面的平行
人教A版2019高二数学(选修一)第一章 空间向量与立体几何
学习目标
能用向量语言描述直线和平面,理解直线的方向向量与平面的法向量.
会求直线的方向向量与平面的法向量.
能用向量语言表述直线与直线、直线与平面、平面与平面的平行关系.
能用向量方法判断或证明直线、平面间的平行关系.
能用向量方法证明必修内容中有关直线、平面位置关系的判断.
问题1:生活中有很多线线平行,线面平行,面面平行的建筑,比如左下图上海世博会的中国馆,右下图是加拿大馆,我们肯定不能仅凭眼睛判断建筑的各个面之间是否平行。
情景导入
下图是武汉大学校门,校门上部的下边线与柱子垂直,我们就能知道下边线与地面平行。这是为什么呢
问题1 如何求直线的方向向量与平面的法向量?
(1)建系
(2)算点
(3)取向量
(4)建方程组
(5)取解
(1)去两点
(2)算向量
(1)算点,设法
(2)取向量:面内两个不共线向量
(3)建方程组
(4)取解
复习回顾
问题2 如何用空间向量表示空间中直线与平面?
直线
平面
方向向量
法向量
位置关系
位置关系
空间向量
立体几何
平行
1.空间中直线、平面的平行
新知探究
问题3 由直线与直线平行的关系,可以得到这两条直线的方向向量有什么关系?
l1
l2
(1)
l1
l2
(1)
直线
方向向量
概念归纳
问题4 由直线与平面平行的关系,可以得到直线的方向向量与平面的法向量有什么关系?
α
l
(2)
m
直线
方向向量
平面
法向量
概念归纳
问题5 由平面与平面平行的关系,可以得到这两个平面的法向量有什么关系?
α
(3)
β
P
m
n
直线
方向向量
平面
法向量
转化
概念归纳
(1)证明“平面与平面平行的判定定理”
(2)证明“直线与平面平行的判定定理”
要求:
1.以小组形式进行讨论;
2.转化成数学语言,利用向量方法解释(数形结合)
3.总结方法
请你用向量的方法证明直线、平面平行相关的判定定理
2.直线、平面平行的判定定理
新知探究
(1)证明“平面与平面平行的判定定理”
α
β
P
b
a
换句话:两个平面的法向量共线
(2)证明“直线与平面平行的判定定理”
α
b
a
换句话:法向量与方向向量垂直
A
B
C
D
D1
A1
B1
C1
x
y
z
P
分析:
是否存在P?
找到P
如何判断
P在哪儿?
P在B1C上
如何表示
A1P//面ACD1
向量运算
确定存在
3.利用空间向量方法求解立体几何中直线、平面平行
新知探究
P30-例3.长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1=2,
线段B1C上是否存在点P,使得A1P∥平面ACD1.
x
y
z
坐标法
A
B
C
D
D1
A1
B1
C1
x
y
z
P
Q
方法二:立体几何先证再猜
作A1D的中点交AD1中于Q
建系
设点
取向量
通用
列方程组
取解
法向量
取两点
得向量
方向向量
运算
概念归纳
已知O为坐标原点,四面体OABC中,A,B,C的坐标分别为A(0,3,5),B(1,2,0),C(0,5,0),若直线AD∥BC且AD交坐标平面Ozx于点D,求点D的坐标.
素养点睛:考查直观想象、数学运算的核心素养.
题型1 空间中的线线平行问题
典例剖析
或0=-(x-1),2=-(y-2),-5=-z.
所以x=1,y=4,z=-5或x=1,y=0,z=5.
故D点坐标为(1,4,-5)或(1,0,5).
向量法处理空间平行问题的两个应用
(1)求字母的值:通过线线、线面、面面平行转化为向量的共线、垂直的关系,再利用向量关系构造关于字母的等量关系,进而求出字母的值.
(2)求点的坐标:可设出对应点的坐标,再利用点与向量的关系,写出对应向量,利用空间中点、线、面的位置关系,转化为向量的位置关系,进而建立与所求点的坐标有关的等式.
概念归纳
如图,在正方体ABCD-A1B1C1D1中,E,F分别为DD1和BB1的中点.求证:四边形AEC1F是平行四边形.
练一练
题型2 向量法证明线面、面面平行问题
(1)若平面α的一个法向量为u1=(-3,y,2),平面β的一个法向量为u2=(6,-2,z),且α∥β,则y+z=________.
(2)如图,在四棱锥S-ABCD中,底面ABCD为正
方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的
中点.求证:EF∥平面SAD.
素养点睛:考查直观想象、数学运算的核心素养.
典例剖析
【答案】(1)-3
1.用向量证明线面平行的方法
(1)证明该直线的方向向量与平面的某一法向量垂直.
(2)证明该直线的方向向量与平面内某直线的方向向量平行.
(3)证明该直线的方向向量可以用平面内的两个不共线的向量线性表示.
2.向量法证明面面平行的方法
设平面α的法向量为n1=(a1,b1,c1),平面β的法向量为n2=(a2,b2,c2),则α∥β n1∥n2 (a1,b1,c1)=k(a2,b2,c2)(k∈R).
概念归纳
练一练
1.用向量方法证明“直线与平面平行的判定定理”:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
l
m
课本练习
A
B
C
D
E
F
A
B
C
D
E
F
此方程组无解
A
B
C
D
D1
A1
B1
C1
F
E
x
y
z
A
B
C
D
D1
A1
B1
C1
F
E
x
y
z
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分析
分层练习-巩固
分层练习-拓展
分层练习-拓展
线线平行
线面平行
面面平行
课堂小结
其中, 分别是直线 的方向向量;
分别是平面 的法向量.
(一)建系;
(二)设点;
(三)表示相关向量;
(四)进行向量运算;
(五)把向量运算的结果”翻译”为几何结论.
数学运算
直观想象
逻辑推理
解决几何问题的步骤.
