人教A版高中数学选择性必修第一册2.1.1倾斜角与斜率 课件(共66张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册2.1.1倾斜角与斜率 课件(共66张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 10:36:52 | ||
图片预览




文档简介
(共66张PPT)
人教版2019高一数学(选修一)第二章 直线和圆的方程
2.1.1 直线的倾斜角与斜率
学习目标
1.理解空间向量的概念.(难点)
2.掌握空间向量的加法、减法、数乘等线性运算.
(重点)
3.掌握共线向量定理、共面向量定理及推论的应用.
(重点、难点)
情景导入
交通工程上一般用“坡度”来描述一段道路对于水平方向的倾斜程度,如图,一辆汽车沿某条道路从A点前进到B点,在水平方向前进的距离为AD,竖直方向上升的高度为DB(如果是下降,则DB的值为负实数),则坡度 .
k>0表示上坡,k<0表示下坡,为了实际应用与安全,在道路铺设时常要规划坡度的大小.
那么坡度是如何来刻画道路的倾斜程度的呢
1.倾斜角与斜率
新知探究
思考与探究:
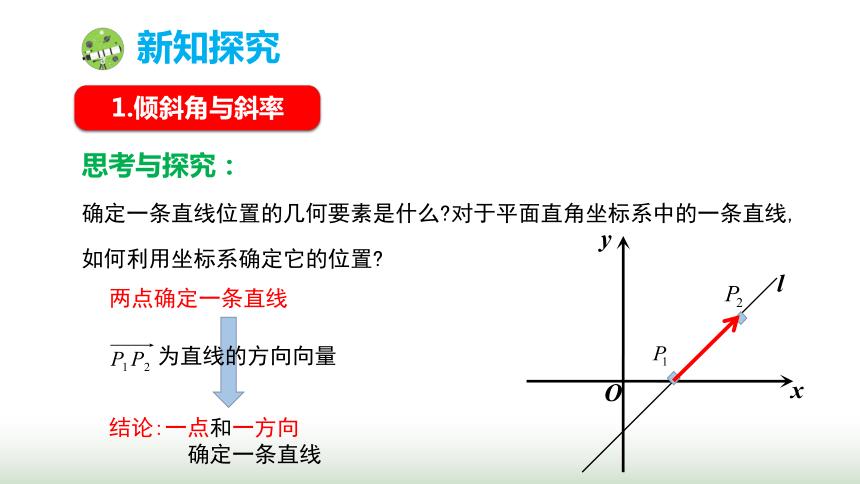
确定一条直线位置的几何要素是什么 对于平面直角坐标系中的一条直线,
如何利用坐标系确定它的位置
x
y
O
l
两点确定一条直线
为直线的方向向量
结论:一点和一方向
确定一条直线
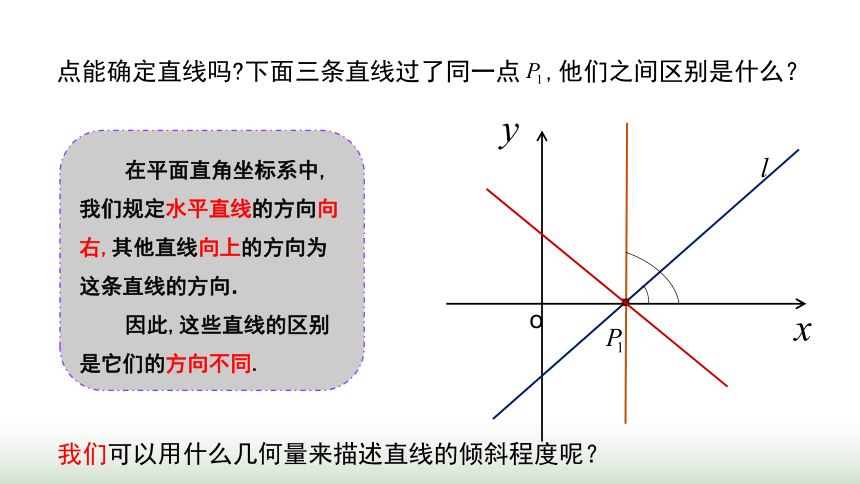
点能确定直线吗 下面三条直线过了同一点 ,他们之间区别是什么?
o
.
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.
因此,这些直线的区别是它们的方向不同.
我们可以用什么几何量来描述直线的倾斜程度呢?
1、定义:
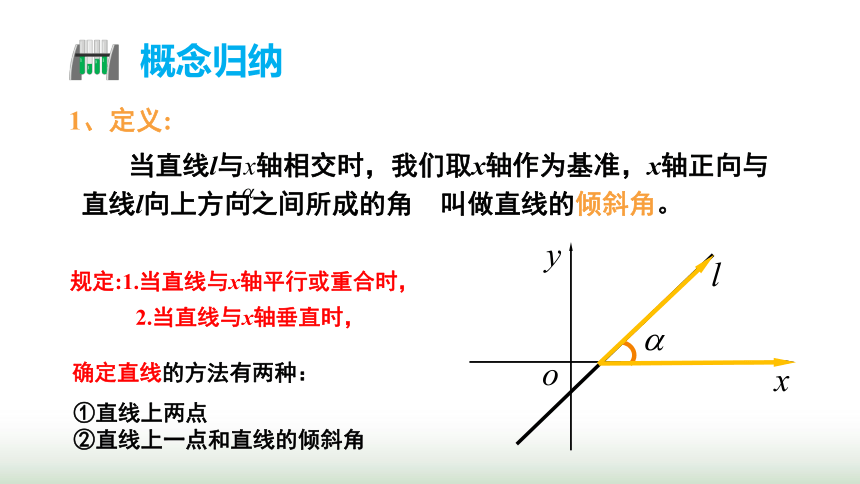
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角 叫做直线的倾斜角。
规定:1.当直线与x轴平行或重合时,
2.当直线与x轴垂直时,
概念归纳
确定直线的方法有两种:
①直线上两点
②直线上一点和直线的倾斜角
o
x
y
o
x
y
o
x
y
o
x
y
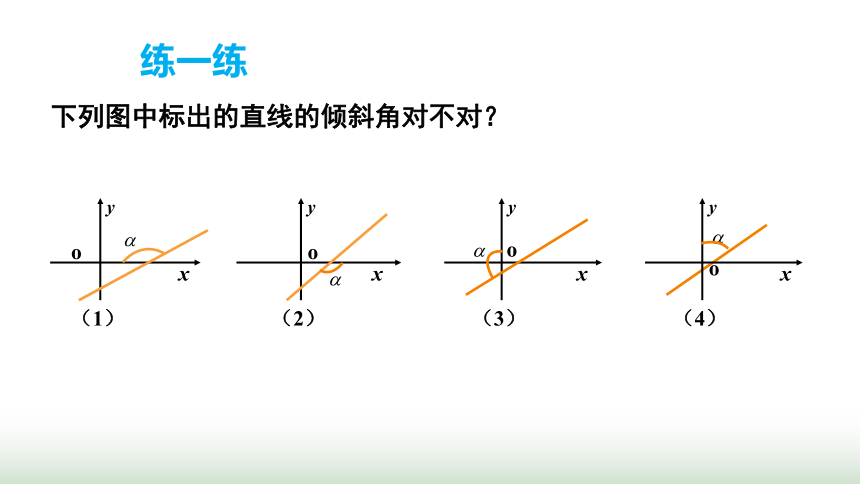
(1)
(2)
(3)
(4)
下列图中标出的直线的倾斜角对不对?
练一练
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
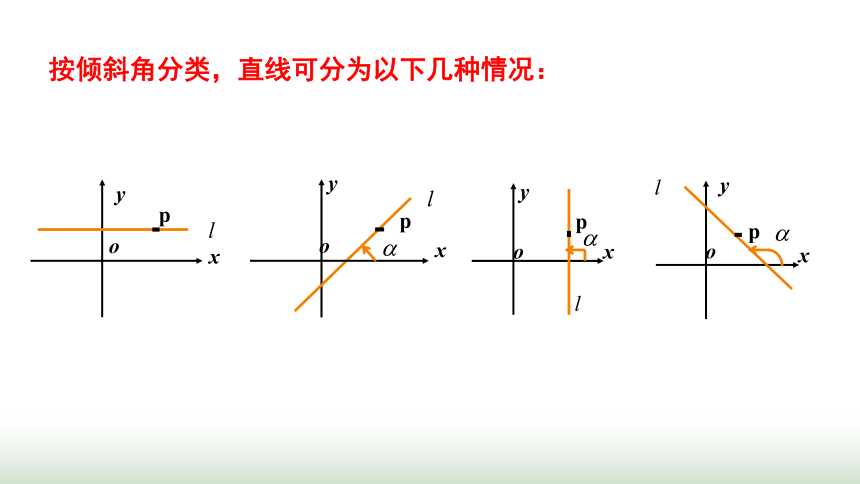
按倾斜角分类,直线可分为以下几种情况:
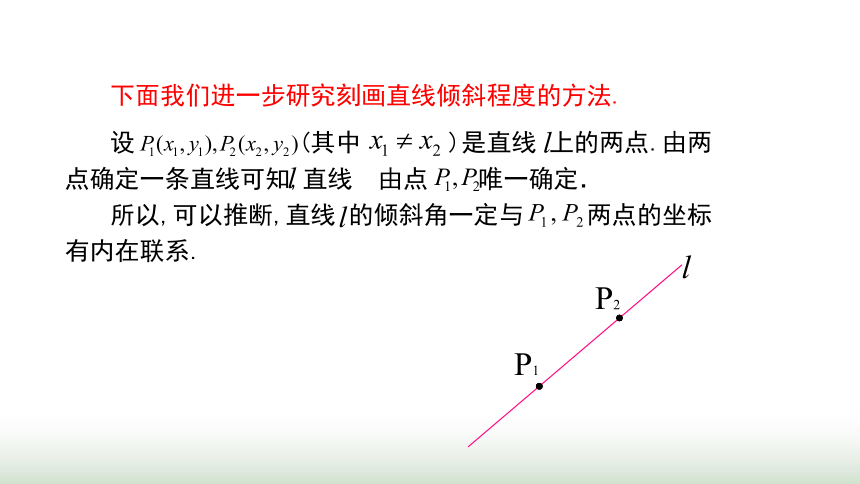
下面我们进一步研究刻画直线倾斜程度的方法.
设 (其中 )是直线 上的两点.由两点确定一条直线可知,直线 由点 唯一确定.
所以,可以推断,直线 的倾斜角一定与 两点的坐标有内在联系.
2.直线的斜率
新知探究
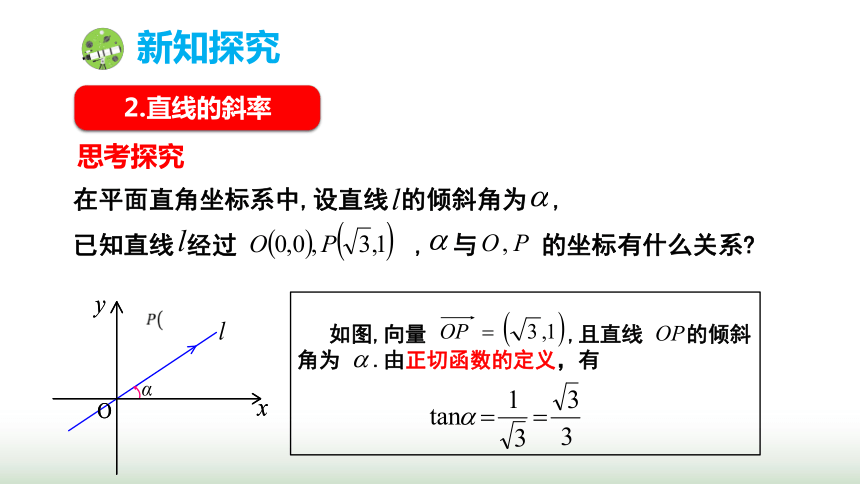
在平面直角坐标系中,设直线 的倾斜角为 ,
已知直线 经过 , 与 的坐标有什么关系
如图,向量 ,且直线 的倾斜角为 .由正切函数的定义,有
思考探究
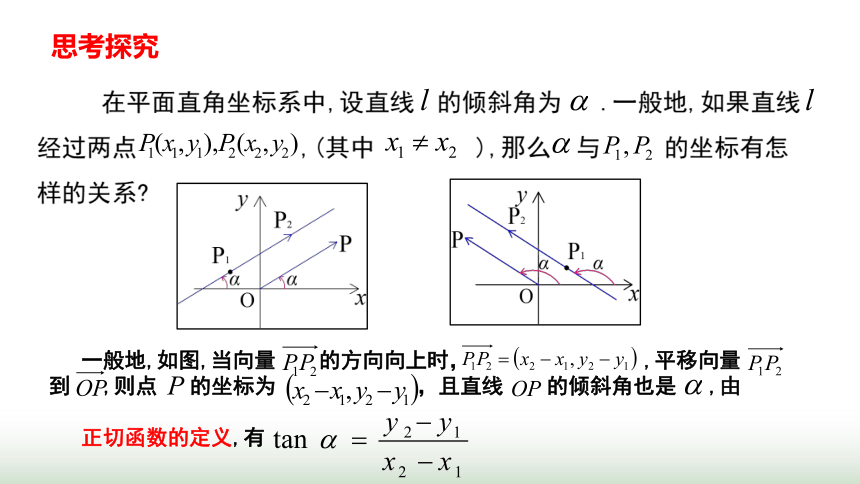
在平面直角坐标系中,设直线 的倾斜角为 .类似地,如果直线经过 , 与 的坐标又有什么关系
如图, .平移向量到 ,则点 的坐标为
且直线 的倾斜角也是 ,由正切函数的定义,有
思考探究
一般地,如图,当向量 的方向向上时, ,平移向量 到 ,则点 的坐标为 ,且直线 的倾斜角也是 ,由
正切函数的定义,有
能不能构造一个直角三角形去求?
当α为锐角时,
倾斜角是锐角时
当α为钝角时,
倾斜角是钝角时
经过两点
的直线的斜率公式:
(1) 当x1=x2时,公式不适用,此时α=900
(2) 直线的斜率可以通过直线上任意两点的坐标来表示
注意:
(3) 与两点的顺序无关
当直线 与 轴平行或重合时,上述式子还成立吗 为什么
当直线 与 轴平行或重合时,
符合
思考探究
概念归纳
综上:直线 的倾斜角 与直线 上的两点
的坐标有如下关系:
我们把一条直线的倾斜角 的正切值叫做这条直线的斜率.
斜率常用小写字母 表示,即
倾斜角是 的直线没有斜率,倾斜角不是 的直线都有斜率.
日常生活中常用“坡度”表示倾斜面的倾斜程度:
前进量
升
高
量
当直线的倾斜角为锐角时,
直线的斜率与坡度是类似的
由图知,
当 时, ,且 随 的增大而增大.
当 时, ,且 随 的增大而增大
当 时,
当 时, 不存在
O
思考探究
由正切函数的单调性,直线的倾斜角不同,其斜率也不同.
o
由
因此,我们也可以用斜率表示倾斜角不等于 的直线相对于 轴的倾斜程度,进而表示直线的方向.
概念归纳
直线 的方向向量 的坐标为 ,
当直线 与 轴不垂直时,即 ,此时向量 ,也是直线 的方向向量,且它的坐标
为 ,即 ,
其中 是直线 的斜率,
直线的方向向量与斜率 有什么关系?
x
y
O
l
结论1 若直线 的斜率为 ,
它的一个方向向量的坐标为 ,则
结论2 若直线 的斜率为 ,
则它的一个方向向量的坐标为
概念归纳
如下图,已知 ,求直线 的斜率,并判断这些直线的倾斜角是锐角还是钝角.
锐角
钝角
锐角
课本例题
(1)下列说法中,正确的是 ( )
A.直线的倾斜角为α,则此直线的斜率为tan α
B.直线的斜率为tan α,则此直线的倾斜角为α
C.若直线的倾斜角为α,则sin α>0
D.任意直线都有倾斜角,但它不一定有斜率
探究一:对直线的倾斜角、斜率的理解
典例剖析
D
(2)设直线l过坐标原点,它的倾斜角为α,如果将直线l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角为 ( )
A.α+45°
B.α-135°
C.135°-α
D.当0°≤α<135°时,倾斜角为α+45°;
当135°≤α<180°时,倾斜角为α-135°
典例剖析
D
【解析】
(1)对于A,当α=90°时,直线的斜率不存在,故不正确;对于B,虽然直线的斜率为tan α,但只有当0°≤α<180°时,α才是此直线的倾斜角,故不正确;对于C,当直线平行于x轴时,α=0°,sin α=0,故C不正确.
(2)根据题意,画出图形,如图所示.
因为0°≤α<180°,显然A,B,C未分类讨论,均不全面,不合题意.通过画图可知:当0°≤α<135°时,倾斜角为α+45°,当135°≤α<180°时,倾斜角为α-135°.
求直线倾斜角的方法及关注点
(1)定义法:根据题意画出图形,结合倾斜角的定义找倾斜角.
(2)关注点:结合图形求角时,应注意平面几何知识的应用,如三角形内角和定理及其有关推论.
1.已知直线l过原点,倾斜角为40°,将直线l顺时针旋转45°得到直线l1,求直线l1的倾斜角.
解:如图,图中角α即为直线l1的倾斜角,
则α=180°-(45°-40°)=
180°-5°=175°.
练一练
3.已知A(3,3),B(-4,2),C(0,-2).
(1)求直线AB和AC的斜率;
(2)点D在线段BC上(包括端点)移动时,求直线AD的斜率的变化范围.
素养点睛:考查直观想象的核心素养.
探究二 有关直线斜率的运算
典例剖析
3.已知A(3,3),B(-4,2),C(0,-2).
点D在线段AB上(包括端点)移动时,求直线CD的斜率的变化范围.
1.利用斜率公式求直线的斜率应注意的事项
(1)运用公式的前提条件是“x1≠x2”,即直线不与x轴垂直,因为当直线与x轴垂直时,斜率是不存在的.
(2)斜率公式与两点P1,P2的先后顺序无关,也就是说公式中的x1与x2,y1与y2可以同时交换位置.
2.由坐标求直线斜率的策略
对于用坐标表示的斜率,其大小与两点的先后顺序无关,当x1=x2,y1≠y2时,直线的倾斜角α=90°,没有斜率,这常常是分类讨论的依据,斜率公式是“数”与“形”结合的纽带.
概念归纳
练一练
若点A(1,1),B(3,5),C(a,7)三点共线,求a的值.
探究三 斜率与倾斜角的综合应用
典例剖析
若点A(1,4),B(3,5),C(a,7)三点共线,求a的值.
练一练
解:因为A(1,1),B(3,5),C(4,7),
由斜率公式得kAB=2,kAC=2,
所以kAB=kAC.
因为直线AB与直线AC的倾斜角相等且过同一点A,
所以直线AB与直线AC为同一条直线.
故A,B,C三点在同一条直线上.
若点A(1,1),B(3,5),C(4,7)三点共线,试证明A,B,C三点在同一条直线上.
练一练
用斜率公式解决三点共线问题的方法
从三点中任取两点,求其斜率
若斜率存在,且相等,且两直线有公共点
若斜率不存在,且两直线有公共点
三点共线
概念归纳
3.已知某直线l的倾斜角α=45°,又P1(2,y1),P2(x2,5),P3(3,1)是此直线上的三点,求x2,y1的值.
练一练
1.若直线l经过A(2,1),B(1,-m2)(m∈R)两点,则直线l的倾斜角α的取值范围是( )
C
随堂练
随堂练
A
3.过点P(-2,m),Q(m,4)的直线的斜率为1,那么m的值为( )
A.1或4 B.4
C.1或3 D.1
随堂练
D
随堂练
60°
课本练习
课本练习
课本练习
课本练习
课本练习
如图,已知点A(-2,3),B(3,2),直线l过点P(0,-2),且与线段AB有公共点,求直线l的斜率k的变化范围.
易错警示 利用直线倾斜角与斜率的关系求解问题
错因分析
错解分析:错误的根本原因是对斜率k与倾斜角间的变化关系理解得不准确.
错因分析
防范措施:正确理解直线倾斜角与斜率的变化求斜率范围问题时,一定要注意对直线倾斜角与斜率的关系的正确理解并灵活应用.如本例直线的倾斜角是从一个锐角逐渐增大到一个钝角,所以直线的斜率应是两个小范围的并集.
错因分析
分层练习-基础
1.若直线过点(1,2),(2,2+),则此直线的倾斜角是( )
A.30° B.45°
C.60° D.90°
2.(2021年合肥月考)若直线l经过原点和点A(-2,-2),则它的斜率为( )
A.-1 B.1
C.1或-1 D.0
C
B
分层练习-基础
4.若三点A(-1,-2),B(4,8),C(5,x)在同一条直线上,则实数x的值为( )
A.10 B.-10
C.5 D.-5
A
A
5.(2021年清远模拟)已知A(3,5),B(5,7),直线l的斜率是直线AB斜率的倍,则直线l的倾斜角为________.
6.设P为x轴上的一点,A(-3,8),B(2,14),若PA的斜率是PB的斜率的两倍,则点P的坐标为________.
分层练习-基础
60°
(-5,0)
8.以下叙述中:(1)任何一条直线都有倾斜角,也有斜率;(2)平行于x轴的直线的倾斜角是0°或180°;(3)直线的斜率范围是(-∞,+∞);(4)过原点的直线,斜率越大越靠近x轴;(5)两条直线的斜率相等,则它们的倾斜角相等;(6)两条直线的倾斜角相等,则它们的斜率相等.其中正确的序号是________.
分层练习-基础
(3)(5)
9.已知点A(1,2),在坐标轴上求一点P使直线PA的倾斜角为60°.
分层练习-基础
分层练习-基础
10.已知交于点M(8,6)的四条直线l1,l2,l3,l4的倾斜角之比为1∶2∶3∶4,又知l2过点N(5,3),求这四条直线的倾斜角.
分层练习-巩固
D
12.(多选)在下列四个命题中,错误的有( )
A.坐标平面内的任何一条直线均有倾斜角和斜率
B.直线的倾斜角的取值范围是[0,π)
C.若一条直线的斜率为tan α,则此直线的倾斜角为α
D.若一条直线的倾斜角为α,则此直线的斜率为tan α
分层练习-巩固
ACD
分层练习-巩固
13.已知三点A(1-a,-5),B(a,2a),C(0,-a)共线,则a=________.
14.在平面直角坐标系中,正三角形ABC的边BC所在直线的斜率是0,则AC,AB所在直线的斜率之和为________.
2
0
分层练习-巩固
15.已知两点A(-3,4),B(3,2),过点C(2,-1)的直线l与线段AB有公共点,求直线l的斜率k的取值范围.
分层练习-巩固
分层练习-巩固
16.已知直线l过点P(3,4),且与以A(-1,0),B(2,1)为端点的线段AB有公共点,求l的斜率k的取值范围.
分层练习-拓展
18.若经过点A(1-t,1+t)和点B(3,2t)的直线的倾斜角α不是锐角,求实数t的取值范围.
分层练习-拓展
课堂小结
1、直线的倾斜角定义及其范围:
2、直线的斜率定义:
3、斜率公式:
人教版2019高一数学(选修一)第二章 直线和圆的方程
2.1.1 直线的倾斜角与斜率
学习目标
1.理解空间向量的概念.(难点)
2.掌握空间向量的加法、减法、数乘等线性运算.
(重点)
3.掌握共线向量定理、共面向量定理及推论的应用.
(重点、难点)
情景导入
交通工程上一般用“坡度”来描述一段道路对于水平方向的倾斜程度,如图,一辆汽车沿某条道路从A点前进到B点,在水平方向前进的距离为AD,竖直方向上升的高度为DB(如果是下降,则DB的值为负实数),则坡度 .
k>0表示上坡,k<0表示下坡,为了实际应用与安全,在道路铺设时常要规划坡度的大小.
那么坡度是如何来刻画道路的倾斜程度的呢
1.倾斜角与斜率
新知探究
思考与探究:
确定一条直线位置的几何要素是什么 对于平面直角坐标系中的一条直线,
如何利用坐标系确定它的位置
x
y
O
l
两点确定一条直线
为直线的方向向量
结论:一点和一方向
确定一条直线
点能确定直线吗 下面三条直线过了同一点 ,他们之间区别是什么?
o
.
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.
因此,这些直线的区别是它们的方向不同.
我们可以用什么几何量来描述直线的倾斜程度呢?
1、定义:
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角 叫做直线的倾斜角。
规定:1.当直线与x轴平行或重合时,
2.当直线与x轴垂直时,
概念归纳
确定直线的方法有两种:
①直线上两点
②直线上一点和直线的倾斜角
o
x
y
o
x
y
o
x
y
o
x
y
(1)
(2)
(3)
(4)
下列图中标出的直线的倾斜角对不对?
练一练
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
按倾斜角分类,直线可分为以下几种情况:
下面我们进一步研究刻画直线倾斜程度的方法.
设 (其中 )是直线 上的两点.由两点确定一条直线可知,直线 由点 唯一确定.
所以,可以推断,直线 的倾斜角一定与 两点的坐标有内在联系.
2.直线的斜率
新知探究
在平面直角坐标系中,设直线 的倾斜角为 ,
已知直线 经过 , 与 的坐标有什么关系
如图,向量 ,且直线 的倾斜角为 .由正切函数的定义,有
思考探究
在平面直角坐标系中,设直线 的倾斜角为 .类似地,如果直线经过 , 与 的坐标又有什么关系
如图, .平移向量到 ,则点 的坐标为
且直线 的倾斜角也是 ,由正切函数的定义,有
思考探究
一般地,如图,当向量 的方向向上时, ,平移向量 到 ,则点 的坐标为 ,且直线 的倾斜角也是 ,由
正切函数的定义,有
能不能构造一个直角三角形去求?
当α为锐角时,
倾斜角是锐角时
当α为钝角时,
倾斜角是钝角时
经过两点
的直线的斜率公式:
(1) 当x1=x2时,公式不适用,此时α=900
(2) 直线的斜率可以通过直线上任意两点的坐标来表示
注意:
(3) 与两点的顺序无关
当直线 与 轴平行或重合时,上述式子还成立吗 为什么
当直线 与 轴平行或重合时,
符合
思考探究
概念归纳
综上:直线 的倾斜角 与直线 上的两点
的坐标有如下关系:
我们把一条直线的倾斜角 的正切值叫做这条直线的斜率.
斜率常用小写字母 表示,即
倾斜角是 的直线没有斜率,倾斜角不是 的直线都有斜率.
日常生活中常用“坡度”表示倾斜面的倾斜程度:
前进量
升
高
量
当直线的倾斜角为锐角时,
直线的斜率与坡度是类似的
由图知,
当 时, ,且 随 的增大而增大.
当 时, ,且 随 的增大而增大
当 时,
当 时, 不存在
O
思考探究
由正切函数的单调性,直线的倾斜角不同,其斜率也不同.
o
由
因此,我们也可以用斜率表示倾斜角不等于 的直线相对于 轴的倾斜程度,进而表示直线的方向.
概念归纳
直线 的方向向量 的坐标为 ,
当直线 与 轴不垂直时,即 ,此时向量 ,也是直线 的方向向量,且它的坐标
为 ,即 ,
其中 是直线 的斜率,
直线的方向向量与斜率 有什么关系?
x
y
O
l
结论1 若直线 的斜率为 ,
它的一个方向向量的坐标为 ,则
结论2 若直线 的斜率为 ,
则它的一个方向向量的坐标为
概念归纳
如下图,已知 ,求直线 的斜率,并判断这些直线的倾斜角是锐角还是钝角.
锐角
钝角
锐角
课本例题
(1)下列说法中,正确的是 ( )
A.直线的倾斜角为α,则此直线的斜率为tan α
B.直线的斜率为tan α,则此直线的倾斜角为α
C.若直线的倾斜角为α,则sin α>0
D.任意直线都有倾斜角,但它不一定有斜率
探究一:对直线的倾斜角、斜率的理解
典例剖析
D
(2)设直线l过坐标原点,它的倾斜角为α,如果将直线l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角为 ( )
A.α+45°
B.α-135°
C.135°-α
D.当0°≤α<135°时,倾斜角为α+45°;
当135°≤α<180°时,倾斜角为α-135°
典例剖析
D
【解析】
(1)对于A,当α=90°时,直线的斜率不存在,故不正确;对于B,虽然直线的斜率为tan α,但只有当0°≤α<180°时,α才是此直线的倾斜角,故不正确;对于C,当直线平行于x轴时,α=0°,sin α=0,故C不正确.
(2)根据题意,画出图形,如图所示.
因为0°≤α<180°,显然A,B,C未分类讨论,均不全面,不合题意.通过画图可知:当0°≤α<135°时,倾斜角为α+45°,当135°≤α<180°时,倾斜角为α-135°.
求直线倾斜角的方法及关注点
(1)定义法:根据题意画出图形,结合倾斜角的定义找倾斜角.
(2)关注点:结合图形求角时,应注意平面几何知识的应用,如三角形内角和定理及其有关推论.
1.已知直线l过原点,倾斜角为40°,将直线l顺时针旋转45°得到直线l1,求直线l1的倾斜角.
解:如图,图中角α即为直线l1的倾斜角,
则α=180°-(45°-40°)=
180°-5°=175°.
练一练
3.已知A(3,3),B(-4,2),C(0,-2).
(1)求直线AB和AC的斜率;
(2)点D在线段BC上(包括端点)移动时,求直线AD的斜率的变化范围.
素养点睛:考查直观想象的核心素养.
探究二 有关直线斜率的运算
典例剖析
3.已知A(3,3),B(-4,2),C(0,-2).
点D在线段AB上(包括端点)移动时,求直线CD的斜率的变化范围.
1.利用斜率公式求直线的斜率应注意的事项
(1)运用公式的前提条件是“x1≠x2”,即直线不与x轴垂直,因为当直线与x轴垂直时,斜率是不存在的.
(2)斜率公式与两点P1,P2的先后顺序无关,也就是说公式中的x1与x2,y1与y2可以同时交换位置.
2.由坐标求直线斜率的策略
对于用坐标表示的斜率,其大小与两点的先后顺序无关,当x1=x2,y1≠y2时,直线的倾斜角α=90°,没有斜率,这常常是分类讨论的依据,斜率公式是“数”与“形”结合的纽带.
概念归纳
练一练
若点A(1,1),B(3,5),C(a,7)三点共线,求a的值.
探究三 斜率与倾斜角的综合应用
典例剖析
若点A(1,4),B(3,5),C(a,7)三点共线,求a的值.
练一练
解:因为A(1,1),B(3,5),C(4,7),
由斜率公式得kAB=2,kAC=2,
所以kAB=kAC.
因为直线AB与直线AC的倾斜角相等且过同一点A,
所以直线AB与直线AC为同一条直线.
故A,B,C三点在同一条直线上.
若点A(1,1),B(3,5),C(4,7)三点共线,试证明A,B,C三点在同一条直线上.
练一练
用斜率公式解决三点共线问题的方法
从三点中任取两点,求其斜率
若斜率存在,且相等,且两直线有公共点
若斜率不存在,且两直线有公共点
三点共线
概念归纳
3.已知某直线l的倾斜角α=45°,又P1(2,y1),P2(x2,5),P3(3,1)是此直线上的三点,求x2,y1的值.
练一练
1.若直线l经过A(2,1),B(1,-m2)(m∈R)两点,则直线l的倾斜角α的取值范围是( )
C
随堂练
随堂练
A
3.过点P(-2,m),Q(m,4)的直线的斜率为1,那么m的值为( )
A.1或4 B.4
C.1或3 D.1
随堂练
D
随堂练
60°
课本练习
课本练习
课本练习
课本练习
课本练习
如图,已知点A(-2,3),B(3,2),直线l过点P(0,-2),且与线段AB有公共点,求直线l的斜率k的变化范围.
易错警示 利用直线倾斜角与斜率的关系求解问题
错因分析
错解分析:错误的根本原因是对斜率k与倾斜角间的变化关系理解得不准确.
错因分析
防范措施:正确理解直线倾斜角与斜率的变化求斜率范围问题时,一定要注意对直线倾斜角与斜率的关系的正确理解并灵活应用.如本例直线的倾斜角是从一个锐角逐渐增大到一个钝角,所以直线的斜率应是两个小范围的并集.
错因分析
分层练习-基础
1.若直线过点(1,2),(2,2+),则此直线的倾斜角是( )
A.30° B.45°
C.60° D.90°
2.(2021年合肥月考)若直线l经过原点和点A(-2,-2),则它的斜率为( )
A.-1 B.1
C.1或-1 D.0
C
B
分层练习-基础
4.若三点A(-1,-2),B(4,8),C(5,x)在同一条直线上,则实数x的值为( )
A.10 B.-10
C.5 D.-5
A
A
5.(2021年清远模拟)已知A(3,5),B(5,7),直线l的斜率是直线AB斜率的倍,则直线l的倾斜角为________.
6.设P为x轴上的一点,A(-3,8),B(2,14),若PA的斜率是PB的斜率的两倍,则点P的坐标为________.
分层练习-基础
60°
(-5,0)
8.以下叙述中:(1)任何一条直线都有倾斜角,也有斜率;(2)平行于x轴的直线的倾斜角是0°或180°;(3)直线的斜率范围是(-∞,+∞);(4)过原点的直线,斜率越大越靠近x轴;(5)两条直线的斜率相等,则它们的倾斜角相等;(6)两条直线的倾斜角相等,则它们的斜率相等.其中正确的序号是________.
分层练习-基础
(3)(5)
9.已知点A(1,2),在坐标轴上求一点P使直线PA的倾斜角为60°.
分层练习-基础
分层练习-基础
10.已知交于点M(8,6)的四条直线l1,l2,l3,l4的倾斜角之比为1∶2∶3∶4,又知l2过点N(5,3),求这四条直线的倾斜角.
分层练习-巩固
D
12.(多选)在下列四个命题中,错误的有( )
A.坐标平面内的任何一条直线均有倾斜角和斜率
B.直线的倾斜角的取值范围是[0,π)
C.若一条直线的斜率为tan α,则此直线的倾斜角为α
D.若一条直线的倾斜角为α,则此直线的斜率为tan α
分层练习-巩固
ACD
分层练习-巩固
13.已知三点A(1-a,-5),B(a,2a),C(0,-a)共线,则a=________.
14.在平面直角坐标系中,正三角形ABC的边BC所在直线的斜率是0,则AC,AB所在直线的斜率之和为________.
2
0
分层练习-巩固
15.已知两点A(-3,4),B(3,2),过点C(2,-1)的直线l与线段AB有公共点,求直线l的斜率k的取值范围.
分层练习-巩固
分层练习-巩固
16.已知直线l过点P(3,4),且与以A(-1,0),B(2,1)为端点的线段AB有公共点,求l的斜率k的取值范围.
分层练习-拓展
18.若经过点A(1-t,1+t)和点B(3,2t)的直线的倾斜角α不是锐角,求实数t的取值范围.
分层练习-拓展
课堂小结
1、直线的倾斜角定义及其范围:
2、直线的斜率定义:
3、斜率公式:
