人教A版高中数学选择性必修第一册1.4.2用空间向量解决立体几何问题(第3课时) 课件(共118张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.4.2用空间向量解决立体几何问题(第3课时) 课件(共118张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 9.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 10:42:41 | ||
图片预览











文档简介
(共118张PPT)
人教A版2019高二数学(选修一)第一章 空间向量与立体几何
第三课时 用空间向量解决立体几何问题
1.4.2 用空间向量研究距离、
夹角问题
学习目标
1.能用向量方法解决简单夹角问题.
2.通过用空间向量解决夹角问题,
3.体会向量方法在研究几何问题中的作用.
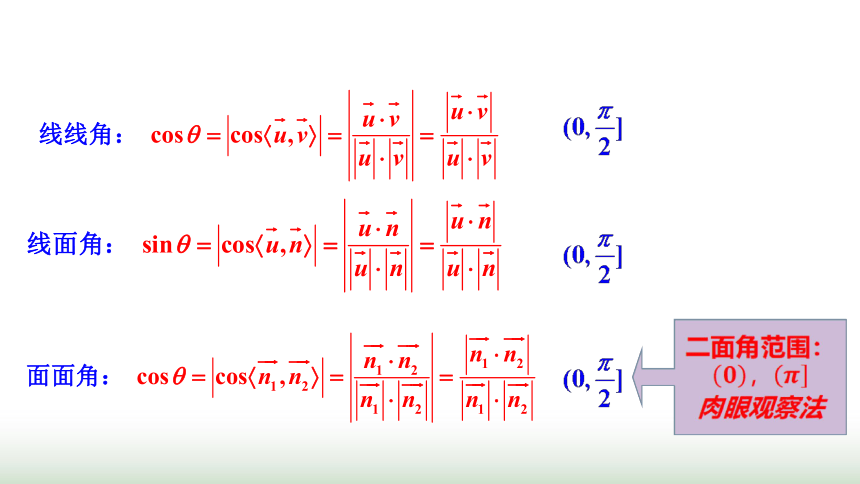
前面我们学习了如何利用空间向量方法求解立体几何中的距离和角度问题,
下面我们再来简单回顾应用一下:
平行关系
情景导入
这节课我们应用之前学习的知识来解决综合性较强的立体几何问题:
用空间向量解决立体几何问题
新知探究
问题1:降落伞在匀速下落的过程中,8根绳子拉力的大小总和与礼物重力大小有什么关系
问题2:降落伞在匀速下落的过程中,8根绳子拉力的和与礼物重力有什么关系
合作探究
大于关系
相反向量
由于8根绳子的合力大小与礼物重力大小相等,所以
所以
问题3:如何用向量方法解决这个问题
典例剖析
问题1:线面平行的几何法证明思路是怎么样分析得到的
问题2:线面平行的向量法证明思路又是怎么样呢
典例剖析
问题3:线面垂直的几何法证明思路是怎么样分析得到的
问题4:发现几何法证明线线垂直有点麻烦,若用向量法怎么样才能证明呢
问题5:求二面角的几何法证明思路是怎么样分析得到的
问题6:用向量思想来求向量夹角,但是如何求出点F 的空间坐标
理解如何求直线上某一点的坐标
问题1:此题用几何法研究线线平行有点难度,但转化为向量法研究线面平行,容易想到研究什么向量?
此时和刚才例题一样,利用设坐标的思想,通过三点共线得到其中两条向量共线,从而找到坐标之间的关系.
问题2:用向量思想来解此题,关键是如何求出点F 的空间坐标
变式练
变式练
问题1:此题二面角的几何法求解思路是怎么样的
问题2:此题二面角的几何法求解思路受阻,请问转换空间向量思想如何来求解
问题1:此题二面角的几何法求解思路是怎么样的
问题2:此题二面角的几何法求解思路受阻,请问转换空间向量思想如何来求解
问题1:此题二面角的几何法求解思路是怎么样的
问题2:此题二面角的几何法求解思路受阻,请问转换空间向量思想
如何来求解
解:
解:
A
B
C
D
E
F
习题1.4
A
C
B
A1
B1
C1
x
y
z
(第2题)
A
C
B
A1
B1
C1
x
y
z
(第2题)
A
C
B
A1
B1
C1
x
y
z
(第2题)
A
C
B
A1
B1
C1
D
D1
F
E
A
C
B
A1
B1
C1
D
D1
F
E
H
A
B
C
D
M
P
Q
x
y
z
A
B
C
D
M
P
Q
x
y
z
A
B
C
D
M
P
Q
H
G
A
B
C
D
M
P
Q
A
C
B
A1
B1
C1
E
D
D1
F
x
y
z
A
C
B
A1
B1
C1
E
D
D1
F
x
y
z
H
A
C
B
A1
B1
C1
E
D
O
D1
x
y
z
A
C
B
A1
B1
C1
E
D
O
D1
x
y
z
O
A
C
D
E
B
H
G
x
y
z
M
7.如图,四面体OABC的所有棱长都是1, D,E分别是OA,BC的中点,连接DE.(1)计算DE的长;(2)求点O到平面ABC的距离.
O
A
C
D
E
B
H
G
x
y
z
M
7.如图,四面体OABC的所有棱长都是1, D,E分别是OA,BC的中点,连接DE.
(1)计算DE的长;(2)求点O到平面ABC的距离.
O
A
C
D
E
B
H
A
B
C
D
M
N
A
B
C
D
M
N
A
B
C
D
M
N
y
z
x
A
B
C
D
M
N
y
z
x
A
B
C
D
D1
C1
B1
A1
E
F
G
H
K
L
y
z
x
A
B
C
D
D1
C1
B1
A1
E
F
G
H
K
L
y
z
x
A
B
C
D
C1
B1
A1
D1
E
x
y
z
A
B
C
D
C1
B1
A1
D1
E
F
G
P
Q
R
A
B
C
D
C1
B1
A1
D1
E
F
G
P
Q
R
A
B
C
D
D1
C1
B1
A1
E
x
y
z
A
B
C
D
D1
C1
B1
A1
E
x
y
z
A
B
C
D
D1
C1
B1
A1
E
A
B
C
D
D1
C1
B1
A1
M
O
x
y
z
A
B
C
D
D1
C1
B1
A1
P
Q
x
y
z
A
B
C
D
D1
C1
B1
A1
P
Q
x
y
z
A
B
C
C1
B1
A1
P
Q
N
x
y
z
M
空间中的直线方程
空间中的平面方程(点法式)
A
B
C
D
M
N
E
F
z
x
y
A
B
C
D
M
N
E
F
z
x
y
A
B
C
D
M
N
E
F
z
x
y
A
B
C
D
M
N
E
F
z
x
y
O
A
B
M
C
N
B
复习参考题
N
A
B
C
D
P
Q
M
N
A
B
C
D
P
Q
M
N
A
B
C
D
P
Q
M
N
A
B
C
D
P
Q
M
A
B
C
M
A1
B1
C1
x
y
z
A
B
C
M
A1
B1
C1
A
B
C
C1
A1
B1
O
z
x
y
A
B
C
C1
A1
B1
O
z
O1
x
y
A
B
C
C1
A1
B1
O
x
y
O1
z
M
N
A
B
C
C1
A1
B1
O
x
y
O1
z
M
N
A
B
C
D
C1
A1
B1
D1
E
F
G
x
y
z
A
B
C
D
C1
A1
B1
D1
E
F
G
x
y
z
C1
A1
B1
A
B
C
M
N
x
y
z
C1
A1
B1
A
B
C
M
N
x
y
z
A
B
C
D
A
B
C
D
A
B
C
D
C1
A1
B1
D1
E
F
A
B
C
D
C1
A1
B1
D1
E
F
x
y
z
A
B
C
D
C1
A1
B1
D1
E
F
x
y
z
A
B
C
D
S
A
B
C
D
S
x
y
z
A
B
D
C
E
O
F
x
y
z
A
B
C
D
P
S
x
y
z
O
A
B
D
C
E
F
G
H
M
A
B
D
C
E
F
G
H
M
A
B
C
O
F
E
x
y
z
A
B
C
O
F
E
G
A
F
E
m
a
n
b
1.平面α的斜线l与它在这个平面上射影l'的方向向量分别为a=(1,0,1),b=(0,1,1),则斜线l与平面α所成的角为( )
A.30° B.45° C.60° D.90°
答案 C
分层练习-基础
2.(2020广东深圳实验学校高二上期中)设平面α与平面β的夹角为θ,若平面α,β的法向量分别为n1,n2,则cos θ=( )
答案 B
分层练习-基础
3.在正方体ABCD-A1B1C1D1中,M,N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
A.30°
45°
C.90°
D.60°
分层练习-基础
解析以D为原点,分别以DA,DC,DD1所在直线为x轴,y轴,z轴建立空间直角坐标系,
答案 D
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD.
(2)若∠CBA=60°,求平面C1OB1与平面OB1D夹角的余弦值.
分层练习-拓展
(1)证明 因为四边形ACC1A1和四边形BDD1B1均为矩形,所以CC1⊥AC,DD1⊥BD,
又CC1∥DD1∥OO1,所以OO1⊥AC,OO1⊥BD,
因为AC∩BD=O,所以O1O⊥底面ABCD.
(2)解 因为四棱柱的所有棱长都相等,所以四边形ABCD为菱形,AC⊥BD.又O1O⊥底面ABCD,所以OB,OC,OO1两两垂直.如图,以O为原点,OB,OC,OO1所在直线分别为x,y,z轴,建立空间直角坐标系.
设棱长为2,因为∠CBA=60°,所以OB= ,OC=1,
所以O(0,0,0),B1( ,0,2),C1(0,1,2),
平面BDD1B1的一个法向量为n=(0,1,0),
分层练习-拓展
分层练习-拓展
用空间向量表示立体图形中点、直线、平面等元素
进行空间向量的运算,研究点、直线、平面之间的关系
把运算结果“翻译”成相应的几何意义
解决立体几何中的问题,可用三种方法:综合法、向量法、坐标法.
课堂小结
人教A版2019高二数学(选修一)第一章 空间向量与立体几何
第三课时 用空间向量解决立体几何问题
1.4.2 用空间向量研究距离、
夹角问题
学习目标
1.能用向量方法解决简单夹角问题.
2.通过用空间向量解决夹角问题,
3.体会向量方法在研究几何问题中的作用.
前面我们学习了如何利用空间向量方法求解立体几何中的距离和角度问题,
下面我们再来简单回顾应用一下:
平行关系
情景导入
这节课我们应用之前学习的知识来解决综合性较强的立体几何问题:
用空间向量解决立体几何问题
新知探究
问题1:降落伞在匀速下落的过程中,8根绳子拉力的大小总和与礼物重力大小有什么关系
问题2:降落伞在匀速下落的过程中,8根绳子拉力的和与礼物重力有什么关系
合作探究
大于关系
相反向量
由于8根绳子的合力大小与礼物重力大小相等,所以
所以
问题3:如何用向量方法解决这个问题
典例剖析
问题1:线面平行的几何法证明思路是怎么样分析得到的
问题2:线面平行的向量法证明思路又是怎么样呢
典例剖析
问题3:线面垂直的几何法证明思路是怎么样分析得到的
问题4:发现几何法证明线线垂直有点麻烦,若用向量法怎么样才能证明呢
问题5:求二面角的几何法证明思路是怎么样分析得到的
问题6:用向量思想来求向量夹角,但是如何求出点F 的空间坐标
理解如何求直线上某一点的坐标
问题1:此题用几何法研究线线平行有点难度,但转化为向量法研究线面平行,容易想到研究什么向量?
此时和刚才例题一样,利用设坐标的思想,通过三点共线得到其中两条向量共线,从而找到坐标之间的关系.
问题2:用向量思想来解此题,关键是如何求出点F 的空间坐标
变式练
变式练
问题1:此题二面角的几何法求解思路是怎么样的
问题2:此题二面角的几何法求解思路受阻,请问转换空间向量思想如何来求解
问题1:此题二面角的几何法求解思路是怎么样的
问题2:此题二面角的几何法求解思路受阻,请问转换空间向量思想如何来求解
问题1:此题二面角的几何法求解思路是怎么样的
问题2:此题二面角的几何法求解思路受阻,请问转换空间向量思想
如何来求解
解:
解:
A
B
C
D
E
F
习题1.4
A
C
B
A1
B1
C1
x
y
z
(第2题)
A
C
B
A1
B1
C1
x
y
z
(第2题)
A
C
B
A1
B1
C1
x
y
z
(第2题)
A
C
B
A1
B1
C1
D
D1
F
E
A
C
B
A1
B1
C1
D
D1
F
E
H
A
B
C
D
M
P
Q
x
y
z
A
B
C
D
M
P
Q
x
y
z
A
B
C
D
M
P
Q
H
G
A
B
C
D
M
P
Q
A
C
B
A1
B1
C1
E
D
D1
F
x
y
z
A
C
B
A1
B1
C1
E
D
D1
F
x
y
z
H
A
C
B
A1
B1
C1
E
D
O
D1
x
y
z
A
C
B
A1
B1
C1
E
D
O
D1
x
y
z
O
A
C
D
E
B
H
G
x
y
z
M
7.如图,四面体OABC的所有棱长都是1, D,E分别是OA,BC的中点,连接DE.(1)计算DE的长;(2)求点O到平面ABC的距离.
O
A
C
D
E
B
H
G
x
y
z
M
7.如图,四面体OABC的所有棱长都是1, D,E分别是OA,BC的中点,连接DE.
(1)计算DE的长;(2)求点O到平面ABC的距离.
O
A
C
D
E
B
H
A
B
C
D
M
N
A
B
C
D
M
N
A
B
C
D
M
N
y
z
x
A
B
C
D
M
N
y
z
x
A
B
C
D
D1
C1
B1
A1
E
F
G
H
K
L
y
z
x
A
B
C
D
D1
C1
B1
A1
E
F
G
H
K
L
y
z
x
A
B
C
D
C1
B1
A1
D1
E
x
y
z
A
B
C
D
C1
B1
A1
D1
E
F
G
P
Q
R
A
B
C
D
C1
B1
A1
D1
E
F
G
P
Q
R
A
B
C
D
D1
C1
B1
A1
E
x
y
z
A
B
C
D
D1
C1
B1
A1
E
x
y
z
A
B
C
D
D1
C1
B1
A1
E
A
B
C
D
D1
C1
B1
A1
M
O
x
y
z
A
B
C
D
D1
C1
B1
A1
P
Q
x
y
z
A
B
C
D
D1
C1
B1
A1
P
Q
x
y
z
A
B
C
C1
B1
A1
P
Q
N
x
y
z
M
空间中的直线方程
空间中的平面方程(点法式)
A
B
C
D
M
N
E
F
z
x
y
A
B
C
D
M
N
E
F
z
x
y
A
B
C
D
M
N
E
F
z
x
y
A
B
C
D
M
N
E
F
z
x
y
O
A
B
M
C
N
B
复习参考题
N
A
B
C
D
P
Q
M
N
A
B
C
D
P
Q
M
N
A
B
C
D
P
Q
M
N
A
B
C
D
P
Q
M
A
B
C
M
A1
B1
C1
x
y
z
A
B
C
M
A1
B1
C1
A
B
C
C1
A1
B1
O
z
x
y
A
B
C
C1
A1
B1
O
z
O1
x
y
A
B
C
C1
A1
B1
O
x
y
O1
z
M
N
A
B
C
C1
A1
B1
O
x
y
O1
z
M
N
A
B
C
D
C1
A1
B1
D1
E
F
G
x
y
z
A
B
C
D
C1
A1
B1
D1
E
F
G
x
y
z
C1
A1
B1
A
B
C
M
N
x
y
z
C1
A1
B1
A
B
C
M
N
x
y
z
A
B
C
D
A
B
C
D
A
B
C
D
C1
A1
B1
D1
E
F
A
B
C
D
C1
A1
B1
D1
E
F
x
y
z
A
B
C
D
C1
A1
B1
D1
E
F
x
y
z
A
B
C
D
S
A
B
C
D
S
x
y
z
A
B
D
C
E
O
F
x
y
z
A
B
C
D
P
S
x
y
z
O
A
B
D
C
E
F
G
H
M
A
B
D
C
E
F
G
H
M
A
B
C
O
F
E
x
y
z
A
B
C
O
F
E
G
A
F
E
m
a
n
b
1.平面α的斜线l与它在这个平面上射影l'的方向向量分别为a=(1,0,1),b=(0,1,1),则斜线l与平面α所成的角为( )
A.30° B.45° C.60° D.90°
答案 C
分层练习-基础
2.(2020广东深圳实验学校高二上期中)设平面α与平面β的夹角为θ,若平面α,β的法向量分别为n1,n2,则cos θ=( )
答案 B
分层练习-基础
3.在正方体ABCD-A1B1C1D1中,M,N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
A.30°
45°
C.90°
D.60°
分层练习-基础
解析以D为原点,分别以DA,DC,DD1所在直线为x轴,y轴,z轴建立空间直角坐标系,
答案 D
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD.
(2)若∠CBA=60°,求平面C1OB1与平面OB1D夹角的余弦值.
分层练习-拓展
(1)证明 因为四边形ACC1A1和四边形BDD1B1均为矩形,所以CC1⊥AC,DD1⊥BD,
又CC1∥DD1∥OO1,所以OO1⊥AC,OO1⊥BD,
因为AC∩BD=O,所以O1O⊥底面ABCD.
(2)解 因为四棱柱的所有棱长都相等,所以四边形ABCD为菱形,AC⊥BD.又O1O⊥底面ABCD,所以OB,OC,OO1两两垂直.如图,以O为原点,OB,OC,OO1所在直线分别为x,y,z轴,建立空间直角坐标系.
设棱长为2,因为∠CBA=60°,所以OB= ,OC=1,
所以O(0,0,0),B1( ,0,2),C1(0,1,2),
平面BDD1B1的一个法向量为n=(0,1,0),
分层练习-拓展
分层练习-拓展
用空间向量表示立体图形中点、直线、平面等元素
进行空间向量的运算,研究点、直线、平面之间的关系
把运算结果“翻译”成相应的几何意义
解决立体几何中的问题,可用三种方法:综合法、向量法、坐标法.
课堂小结
