人教A版高中数学选择性必修第一册2.2.1直线的点斜式方程 课件(共62张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册2.2.1直线的点斜式方程 课件(共62张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 10:43:18 | ||
图片预览










文档简介
(共62张PPT)
人教版2019高一数学(选修一) 第二章 直线和圆的方程
2.2.1 直线的点斜式方程
学习目标
1.了解由斜率公式推导直线方程的点斜式的过程(重点)
2.掌握直线的点斜式方程和斜截式方程,并会用它们
求直线的方程(难点)
3.会利用直线的点斜式和斜截式方程解决有关的问题
情景导入
如图所示,在平面直角坐标系中,直线l过点P(0,3),斜率k=-2,Q(x,y)是直线l上不同于P的任意一点,由于P,Q都在l上,所以可以用P,Q的坐标来表示直线l的斜率, =2,即得方程y=2x+3.
这表明直线l上任一点的坐标(x,y)都满足y=2x+3.那么满足方程y=2x+3的每一组(x,y)所对应的点也都在直线l上吗
本节课我们学习直线的点斜式方程解决这个问题.
1.直线的点斜式方程
新知探究
(x,y)
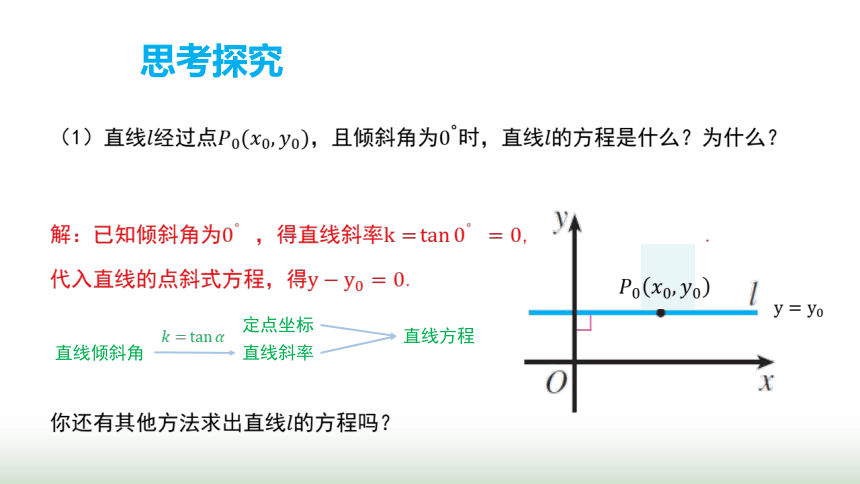
思考探究
思考探究
概念归纳
点斜式
概念归纳
思考探究
定点坐标
直线斜率
直线方程
直线倾斜角
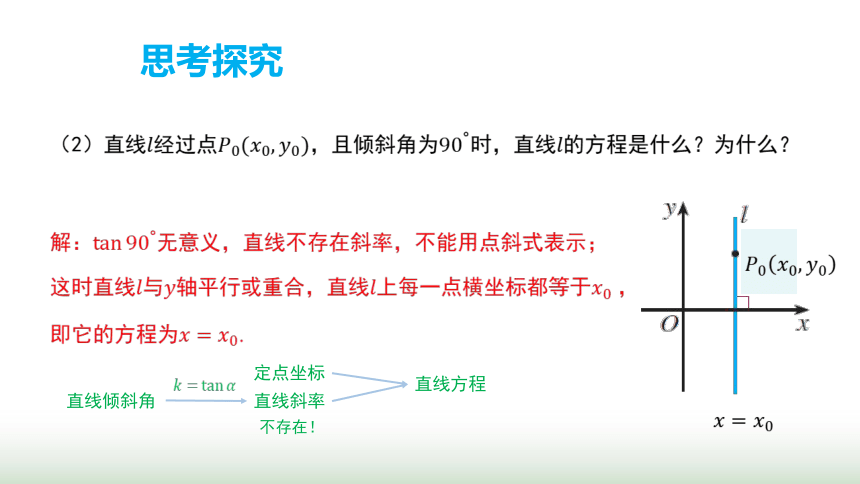
思考探究
定点坐标
直线斜率
直线方程
直线倾斜角
不存在!
概念归纳
课本例题
2.直线的斜截式方程
新知探究
概念归纳
思考探究
课本例题
求满足下列条件的直线的点斜式方程.
(1)过点P(4,-2),倾斜角为150°;
(2)过点P(20,-19),且与x轴平行;
(3)过点Q(-6,2),且与y轴平行;
(4)过P(1,3),Q(2,5)两点.
题型1 求直线的点斜式方程
典例剖析
典例剖析
典例剖析
求直线的点斜式方程的步骤
斜率是否存在
由点斜式写方程
提醒:斜率不存在时,过点P(x0,y0)的直线与x轴垂直,直线上所有点的横坐标相等,都为x0,故直线方程为x=x0.
是
否
归纳总结
1.已知直线l过点P(3,4),它的倾斜角是直线y=x+1倾斜角的两倍,则直线l的方程为 ( )
A.y-4=2(x-3) B.y-4=x-3
C.y-4=0 D.x-3=0
【解析】直线y=x+1的倾斜角为45°,由题意得直线l的倾斜角为90°,所以直线l的斜率不存在,其方程为x-3=0.
D
练一练
2.一条直线经过点P(-2,3),且与过点(-4,4)和(-3,2)的直线平行,求这条直线的方程.
练一练
已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1平行且与l2在y轴上的截距相同,求直线l的方程.
题型2 求直线的斜截式方程
典例剖析
解:由斜截式方程知直线l1的斜率k1=-2.
又因为l∥l1,所以l的斜率k=k1=-2.
由题意知l2在y轴上的截距为-2,
所以l在y轴上的截距b=-2.
由斜截式方程可得直线l的方程为y=-2x-2.
已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1垂直且与l2在y轴上的截距相同,求直线l的方程.
典例剖析
解:由斜截式方程知直线l1的斜率k1=-2.
又因为l∥l1,所以l的斜率k=k1=-2.
由题意知l2在y轴上的截距为-2,
所以l在y轴上的截距b=2.
由斜截式方程可得直线l的方程为y=-2x+2.
已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1垂直且与l2在y轴上的截距互为相反数,求直线l的方程.
典例剖析
求直线的斜截式方程的策略
(1)直线的斜截式方程是点斜式方程的特殊形式,其适用前提是直线的斜率存在,只要点斜式中的点在y轴上,就可以直接用斜截式表示.
(2)直线的斜截式方程y=kx+b中只有两个参数,因此要确定直线方程,只需知道参数k,b的值即可.
(3)利用直线的斜截式求方程务必灵活,如果已知斜率k,只需引入参数b;同理如果已知截距b,只需引入参数k.
归纳总结
3.直线l与直线l1:y=3x+6在y轴上有相同的截距,且l的斜率与l1的斜率互为相反数,求直线l的方程.
练一练
解:由直线l1的方程可知它的斜率为3,在y轴上的截距为6,
所以直线l的斜率为-3,在y轴上的截距为6.
由斜截式可得直线l的方程为y=-3x+6.
已知直线l1:y=-x+3a与直线l2:y=(a2-5)x+6.
(1)当a为何值时,l1∥l2
(2)当a为何值时,l1⊥l2
典例剖析
题型3 两直线垂直和平行的应用
两条直线平行和垂直的判定
(1)平行的判定.
归纳总结
(1)垂直的判定.
归纳总结
4.在△ABC中,已知A(0,0),B(3,1),C(1,3).
(1)求AB边上的高所在直线的方程;
(2)求BC边上的高所在直线的方程;
(3)求过点A与BC平行的直线方程.
练一练
练一练
1.与直线y=3x+1垂直,且过点(2,-1)的直线的斜截式方程是( )
随堂练
2.已知直线l:y=kx+b(k≠0),且l不经过第三象限,若x∈[2,4]时,y∈[-1,1],则k,b的值分别为( )
A.k=2,b=3 B.k=-2,b=3
C.k=1,b=1 D.k=-1,b=3
B
D
3.直线 l 的倾斜角为45°,在y轴上的截距为-2的直线方程为 .
随堂练
y=x-2
4.直线l1与直线l2:y=3x+1平行,又直线l1过点(3,5),则直线l1的方程为 .
y=3x-4
课本练习
课本练习
1
课本练习
课本练习
课本练习
错因分析
易错警示 求直线的斜截式方程
已知直线l的斜率为3,且与两坐标轴围成的三角形的面积为6,则直线l的方程为________.
错解分析:错误的根本原因是误认为b是边长或是距离,只能取正值,混淆截距的概念,没有真正理解截距的定义实质.
错因分析
概念归纳
防范措施:准确理解截距的概念
直线在y轴上的截距是直线与y轴的交点的纵坐标,可正,可负,可为零,截距不是距离,若把截距理解为正值,则易漏解.
分层练习-基础
B
分层练习-基础
3.已知直线l1:y=2x+3a,l2:y=(a2+1)x+3,若l1∥l2,则a=( )
A.0 B.-1
C.1 D.±1
A
B
分层练习-基础
5.已知直线l的方程为y-m=(m-1)(x+1),若l在y轴上的截距为7,则m=________.
B
4
分层练习-基础
6.直线y=x+1绕其与y轴交点旋转90°的直线方程是________.
7.直线y=2x-4绕着它与x轴的交点逆时针旋转90°后,所得的直线方程为____________.
8.直线l经过点A(-2,2)且与直线y=x+6在y轴上有相同的截距,则直线l的斜截式方程为____________.
y=-x+1
y=2x+6
分层练习-基础
分层练习-基础
10.求下列直线的斜截式方程:
(1)斜率为-4,在y轴上的截距为7;
(2)在y轴上的截距为2,且与x轴平行;
(3)求倾斜角为150°,与y轴的交点到原点的距离为3的直线方程.
分层练习-基础
分层练习-巩固
ABC
分层练习-巩固
12.已知直线kx-y+1-3k=0,当k变化时,所有的直线恒过定点( )
A.(1,3) B.(-1,-3)
C.(3,1) D.(-3,-1)
14.在y轴上的截距为-6,且与y轴相交成30°角的直线方程是__________.
C
y=-2x+1
分层练习-巩固
15.求过点(1,2)且与两坐标轴组成一等腰直角三角形的直线方程,并化成斜截式方程.
解:因为直线与坐标轴组成一等腰直角三角形,
所以k=±1.
又因为直线过点(1,2),
代入点斜式方程得y-2=x-1或y-2=-(x-1),
即y=x+1或y=-x+3.
分层练习-巩固
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
分析:
画图形
建立坐标系
求灯罩轴线所在直线
得出解
分层练习-拓展
分层练习-拓展
课堂小结
两种直线方程
直线方程 几何要素 适用范围
人教版2019高一数学(选修一) 第二章 直线和圆的方程
2.2.1 直线的点斜式方程
学习目标
1.了解由斜率公式推导直线方程的点斜式的过程(重点)
2.掌握直线的点斜式方程和斜截式方程,并会用它们
求直线的方程(难点)
3.会利用直线的点斜式和斜截式方程解决有关的问题
情景导入
如图所示,在平面直角坐标系中,直线l过点P(0,3),斜率k=-2,Q(x,y)是直线l上不同于P的任意一点,由于P,Q都在l上,所以可以用P,Q的坐标来表示直线l的斜率, =2,即得方程y=2x+3.
这表明直线l上任一点的坐标(x,y)都满足y=2x+3.那么满足方程y=2x+3的每一组(x,y)所对应的点也都在直线l上吗
本节课我们学习直线的点斜式方程解决这个问题.
1.直线的点斜式方程
新知探究
(x,y)
思考探究
思考探究
概念归纳
点斜式
概念归纳
思考探究
定点坐标
直线斜率
直线方程
直线倾斜角
思考探究
定点坐标
直线斜率
直线方程
直线倾斜角
不存在!
概念归纳
课本例题
2.直线的斜截式方程
新知探究
概念归纳
思考探究
课本例题
求满足下列条件的直线的点斜式方程.
(1)过点P(4,-2),倾斜角为150°;
(2)过点P(20,-19),且与x轴平行;
(3)过点Q(-6,2),且与y轴平行;
(4)过P(1,3),Q(2,5)两点.
题型1 求直线的点斜式方程
典例剖析
典例剖析
典例剖析
求直线的点斜式方程的步骤
斜率是否存在
由点斜式写方程
提醒:斜率不存在时,过点P(x0,y0)的直线与x轴垂直,直线上所有点的横坐标相等,都为x0,故直线方程为x=x0.
是
否
归纳总结
1.已知直线l过点P(3,4),它的倾斜角是直线y=x+1倾斜角的两倍,则直线l的方程为 ( )
A.y-4=2(x-3) B.y-4=x-3
C.y-4=0 D.x-3=0
【解析】直线y=x+1的倾斜角为45°,由题意得直线l的倾斜角为90°,所以直线l的斜率不存在,其方程为x-3=0.
D
练一练
2.一条直线经过点P(-2,3),且与过点(-4,4)和(-3,2)的直线平行,求这条直线的方程.
练一练
已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1平行且与l2在y轴上的截距相同,求直线l的方程.
题型2 求直线的斜截式方程
典例剖析
解:由斜截式方程知直线l1的斜率k1=-2.
又因为l∥l1,所以l的斜率k=k1=-2.
由题意知l2在y轴上的截距为-2,
所以l在y轴上的截距b=-2.
由斜截式方程可得直线l的方程为y=-2x-2.
已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1垂直且与l2在y轴上的截距相同,求直线l的方程.
典例剖析
解:由斜截式方程知直线l1的斜率k1=-2.
又因为l∥l1,所以l的斜率k=k1=-2.
由题意知l2在y轴上的截距为-2,
所以l在y轴上的截距b=2.
由斜截式方程可得直线l的方程为y=-2x+2.
已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1垂直且与l2在y轴上的截距互为相反数,求直线l的方程.
典例剖析
求直线的斜截式方程的策略
(1)直线的斜截式方程是点斜式方程的特殊形式,其适用前提是直线的斜率存在,只要点斜式中的点在y轴上,就可以直接用斜截式表示.
(2)直线的斜截式方程y=kx+b中只有两个参数,因此要确定直线方程,只需知道参数k,b的值即可.
(3)利用直线的斜截式求方程务必灵活,如果已知斜率k,只需引入参数b;同理如果已知截距b,只需引入参数k.
归纳总结
3.直线l与直线l1:y=3x+6在y轴上有相同的截距,且l的斜率与l1的斜率互为相反数,求直线l的方程.
练一练
解:由直线l1的方程可知它的斜率为3,在y轴上的截距为6,
所以直线l的斜率为-3,在y轴上的截距为6.
由斜截式可得直线l的方程为y=-3x+6.
已知直线l1:y=-x+3a与直线l2:y=(a2-5)x+6.
(1)当a为何值时,l1∥l2
(2)当a为何值时,l1⊥l2
典例剖析
题型3 两直线垂直和平行的应用
两条直线平行和垂直的判定
(1)平行的判定.
归纳总结
(1)垂直的判定.
归纳总结
4.在△ABC中,已知A(0,0),B(3,1),C(1,3).
(1)求AB边上的高所在直线的方程;
(2)求BC边上的高所在直线的方程;
(3)求过点A与BC平行的直线方程.
练一练
练一练
1.与直线y=3x+1垂直,且过点(2,-1)的直线的斜截式方程是( )
随堂练
2.已知直线l:y=kx+b(k≠0),且l不经过第三象限,若x∈[2,4]时,y∈[-1,1],则k,b的值分别为( )
A.k=2,b=3 B.k=-2,b=3
C.k=1,b=1 D.k=-1,b=3
B
D
3.直线 l 的倾斜角为45°,在y轴上的截距为-2的直线方程为 .
随堂练
y=x-2
4.直线l1与直线l2:y=3x+1平行,又直线l1过点(3,5),则直线l1的方程为 .
y=3x-4
课本练习
课本练习
1
课本练习
课本练习
课本练习
错因分析
易错警示 求直线的斜截式方程
已知直线l的斜率为3,且与两坐标轴围成的三角形的面积为6,则直线l的方程为________.
错解分析:错误的根本原因是误认为b是边长或是距离,只能取正值,混淆截距的概念,没有真正理解截距的定义实质.
错因分析
概念归纳
防范措施:准确理解截距的概念
直线在y轴上的截距是直线与y轴的交点的纵坐标,可正,可负,可为零,截距不是距离,若把截距理解为正值,则易漏解.
分层练习-基础
B
分层练习-基础
3.已知直线l1:y=2x+3a,l2:y=(a2+1)x+3,若l1∥l2,则a=( )
A.0 B.-1
C.1 D.±1
A
B
分层练习-基础
5.已知直线l的方程为y-m=(m-1)(x+1),若l在y轴上的截距为7,则m=________.
B
4
分层练习-基础
6.直线y=x+1绕其与y轴交点旋转90°的直线方程是________.
7.直线y=2x-4绕着它与x轴的交点逆时针旋转90°后,所得的直线方程为____________.
8.直线l经过点A(-2,2)且与直线y=x+6在y轴上有相同的截距,则直线l的斜截式方程为____________.
y=-x+1
y=2x+6
分层练习-基础
分层练习-基础
10.求下列直线的斜截式方程:
(1)斜率为-4,在y轴上的截距为7;
(2)在y轴上的截距为2,且与x轴平行;
(3)求倾斜角为150°,与y轴的交点到原点的距离为3的直线方程.
分层练习-基础
分层练习-巩固
ABC
分层练习-巩固
12.已知直线kx-y+1-3k=0,当k变化时,所有的直线恒过定点( )
A.(1,3) B.(-1,-3)
C.(3,1) D.(-3,-1)
14.在y轴上的截距为-6,且与y轴相交成30°角的直线方程是__________.
C
y=-2x+1
分层练习-巩固
15.求过点(1,2)且与两坐标轴组成一等腰直角三角形的直线方程,并化成斜截式方程.
解:因为直线与坐标轴组成一等腰直角三角形,
所以k=±1.
又因为直线过点(1,2),
代入点斜式方程得y-2=x-1或y-2=-(x-1),
即y=x+1或y=-x+3.
分层练习-巩固
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
分析:
画图形
建立坐标系
求灯罩轴线所在直线
得出解
分层练习-拓展
分层练习-拓展
课堂小结
两种直线方程
直线方程 几何要素 适用范围
